RBSE Class 12 Maths Important Questions Chapter 11 Three Dimensional Geometry

Rajasthan Board RBSE Class 12 Maths Important Questions Chapter 11 Three Dimensional Geometry Important Questions and Answers.

RBSE Class 12 Maths Chapter 11 Important Questions Three Dimensional Geometry

Question 1.
Find the direction cosines of line joining points (- 2, 4, - 5) and (1, 2, 3).
Answer:
Let P = (x₁, y₁, z₁) = (- 2, 4, - 5)
and Q = (x₂, y₂, z₂) = (1, 2, 3)
Formula for direction cosines of line joining point P and Q.
\(\frac{x_2-x_1}{P Q}, \frac{y_2-y_1}{P Q}, \frac{z_2-z_1}{P Q}\)Here x₁ = - 2, y₁ = 4, z₁ = - 5 and x₂ = 1, y₂ = 2, z₂ = 3, then

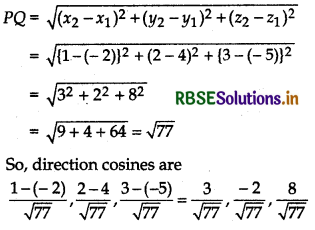
Question 2.
Find direction cosines of line
\(\frac{x-2}{2}=\frac{y+1}{-2}=\frac{z-1}{1}\)
Answer:
Given equation of line is

Question 3.
Write the distance of a point P(a, b, c) from X-axis.
Answer:
Given point is P(a, b, c).
Then, the coordinates of the point on X-axis be (a, 0, 0).
[∵ x-coordinate of both points will be same]
∴ Required distance

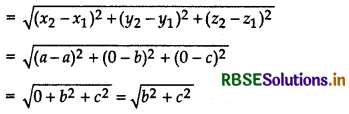
Question 4.
Write the cartesian form of line passing through point (1, 0, 2) and (4, 5, 6).
Answer:
Here, x₁ = 1, y₁ = 0, z₁ = 2
and x₂ = 4, y₂ = 5, z₂ = 6
Equation of line \(\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}\)
= \(\frac{x-1}{3}=\frac{y}{5}=\frac{z-2}{4}\)

Question 5.
Find the shortest distance between lines
\(\frac{x-1}{1}=\frac{y-2}{-1}=\frac{z-1}{1}\)
and \(\frac{x-2}{2}=\frac{y+1}{1}=\frac{z+1}{2}.\)
Answer:
Equation of given lines are

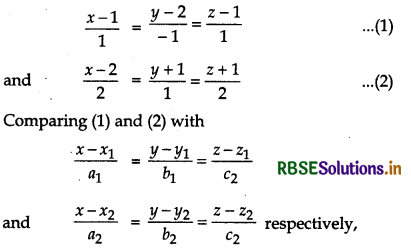
we get (x₁ = 1, y₁ = 2, z₁ = 1)
(x₂ = 2, y₂ = - 1, z₂ = - 1)
(a₁ = 1, b₁ = - 1, c₁ = 1)
(a₂ = 2, b₂ = 1, c₂ = 2)
∴ Shortest distance
= \(\frac{\left|\begin{array}{ccc} x_2-x_1 & y_2-y_1 & z_2-z_1 \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{array}\right|}{\sqrt{D}}\)
D = [(a₁b₂ - b₁a₂)² + (b₁c₂ - b₂c₁)² + (c₁a₂ - c₂a₁)²
= [(1 × 1 - 2 × - 1)² + (2 × - 1 - 1 × 1)² + (1 × 2 - 2 × 1)²]
= [(1 + 2)² + (- 2 - 1)² + (2 - 2)²]
= [3² + (- 3)² + 0²]
= 9 + 9 = 18

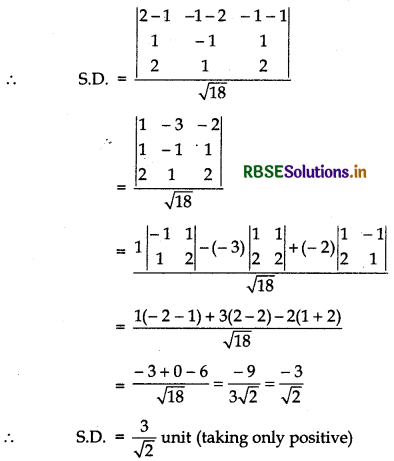
Question 6.
Show that the lines \(\frac{5-x}{-4}=\frac{y-7}{4}=\frac{z+3}{-5}\) and \(\frac{x-8}{7}=\frac{2 y-8}{2}=\frac{z-5}{3}\) are coplanar.
Answer:
Given lines can be written as
\(\frac{x-5}{4}=\frac{y-7}{4}=\frac{z+3}{-5}\)
and \(\frac{x-8}{7}=\frac{y-4}{1}=\frac{z-5}{3}\)
On comparing both lines with,
\(\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{b}\)
respectively, we get
x₁ = 5, y₁ = 7, z₁ = - 3, a₁ = 4, b₁ = 4, c₁ = -5
and x₂ = 8, y₂ = 4, z₂ = 5, a₂ = 7, b₂ = 1, c₂ = 3
If given lines are coplanar, then

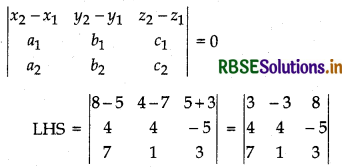
= 3(12 + 5) + 3(12 + 35) + 8(4 - 28)
= 3 × 17 + 3 × 47 + 8(- 24)
= 51 + 141 - 192
= 192 - 192 = 0 = RHS
Therefore, given lines are coplanar.
Hence proved.

Question 7.
Write the intercepts cut-off by plane 2x + y - z = 5 on x-axis.
Answer:
Given equation of plane is 2x + y - z = 5
On dividing both sides by 5, we get
\(\frac{2 x}{5}+\frac{y}{5}-\frac{z}{5}\) = 1 ⇒ \(\frac{x}{\left(\frac{5}{2}\right)}+\frac{y}{5}+\frac{z}{(-5)}\) = 1
On comparing above equation of plane with the intercept form of equation of plane
\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1
where a = x-intercept, b = y-intercept and c = z-intercept
we get, a = \(\frac{5}{2}\)
i.e. intercept cut-off on X-axis = \(\frac{5}{2}\) units

Question 8.
Find the vector equation of the plane through the points (2, 1, - 1) and (- 1, 3,4) and perpendicular to the plane x - 2y + 4z = 10.
Answer:
The required plane passes through two points P(2, 1, - 1) and Q(- 1, 3, 4).
Let \(\vec{a}\) and \(\vec{b}\) be the position vectors of points P and Q, respectively.
Then, \(\vec{a}\) = 2î + ĵ - k̂
and \(\vec{b}\) = - î + 3ĵ + 4k̂
Now, \(\overrightarrow{P Q}\) = \(\vec{b}-\vec{a}\) = (- î + 3ĵ + 4k̂) - (2î + ĵ - k̂)
= - 3î + 2ĵ + 5k̂
Let \(\vec{n}_1\) be the normal vector to the given plane,
x - 2y + 4z = 10, then \(\vec{n}_1\) = î - 2ĵ + 4k̂
Let \(\vec{n}\) be the normal vector to the required plane.
Then,
\(\vec{n}\) = \(\overrightarrow{n_1} \times \overrightarrow{P Q} = \left|\begin{array}{rrr} \hat{i} & \hat{j} & \hat{k} \\ 1 & -2 & 4 \\ -3 & 2 & 5 \end{array}\right|\)
= î(- 10 - 8) - ĵ(5 + 12) + k̂(2 - 6)
= - 18î - 17ĵ - 4k̂
The required plane passes through a point having position vector \(\vec{a}\) = 2î + ĵ - k̂ and normal vector \(\vec{n}\) = - 18î - 17ĵ - 4k̂ . So, its vector equation is
\((\vec{r}-\vec{a}) \cdot \vec{n} \Rightarrow \vec{r} \cdot \vec{n}=\vec{a} \cdot \vec{n}\)
⇒ \(\vec{r}\). (- 18î - 17ĵ - 4k̂) = (2î + ĵ - k̂) (- 18î - 17ĵ - 4k̂)
⇒ \(\vec{r}\).(- 18î - 17ĵ - 4k̂) = - 36 - 17 + 4
∴ \(\vec{r}\). (18î + 17ĵ + 4k̂) = 49

Question 9.
Find the vector and certesian forms of the equation of the plane passing through the point (1, 2, -4) and parallel to the lines
\(\vec{r}\) = î + 2ĵ - 4k̂ + λ(2î + 3ĵ + 6k̂) and \(\vec{r}\) = î - 3ĵ + 5k̂+ μ(î + ĵ - k̂). Also, find the distance of the point (9, - 8, - 10) from the plane thus obtained.
Answer:
Let equation of plane through (1, 2, -4) be
a(x - 1) + b(y - 2) + c(z + 4) = 0
Given lines are
\(\vec{r}\) = î + 2ĵ - 4k̂ + λ(2î + 3ĵ + 6k̂)
and \(\vec{r}\) = î - 3ĵ + 5k̂+ μ(î + ĵ - k̂)
The cartesian equations of given lines are
\(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z+4}{6}\) and \(\frac{x-1}{1}=\frac{y+3}{1}=\frac{z-5}{1}\)
Since, the required plane (j) is parallel in the given lines,
so normal to the plane is perpendicular to the given lines.
∴ 2a + 3b + 6c = 0
and a + b + c = 0
For solving these two equations by cross-multiplication,
we get
\(\frac{a}{-3-6}=\frac{b}{6+2}=\frac{c}{2-3}\) ⇒ \(\frac{a}{-9}=\frac{b}{8}=\frac{c}{-1}\) = λ(say)
∴ a = - 9λ, b = 8λ, c = - λ
On putting values of a, b and c in Eq. (i), we get
- 9λ(x - 1) + 8λ(y - 2) - λ(z + 4) = 0
Equation of plane in cartesian form is
- 9λ (x - 1) + 8λ (y - 2) - λ(z + 4) = 0
⇒ - 9x + 9 + 8y - 16 - z - 4 = 0
⇒ 9x - 8y + z + 11 = 0
Now, vector from of plane is
\(\vec{r}\) . (9î - 8ĵ + k̂) = - 11
Also, distance of (9, - 8, - 10) from the above plane

Multiple Choice Questions

Question 1.
The lines \(\frac{x-2}{1}=\frac{y-3}{1}=\frac{4-z}{k}\) and \(\frac{x-1}{k}=\frac{y-4}{2}=\frac{z-5}{-2}\) are mutually perpendicular, if the value of k is:
(a) - \(\frac{2}{3}\)
(b) \(\frac{2}{3}\)
(c) - 2
(d) 2
Answer:
(a) - \(\frac{2}{3}\)

Question 2.
The two lines x = ay + b, z = cy + d; and x = a’y + b’,z = c’y + d' are perpendicular to each other, if:
(a) \(\frac{a}{a^{\prime}}+\frac{c}{c^{\prime}}\) = 1
(b) \(\frac{a}{a^{\prime}}+\frac{c}{c^{\prime}}\) = - 1
(c) aa’ + cc’ = 1
(d) aa’ + cc’ = - 1
Answer:
(d) aa’ + cc’ = - 1

Question 3.
The two planes x - 2y + 4z = 10 and 18x + 17y + kz = 50 are perpendicular, if k is equal to:
(a) - 4
(b) 4
(c) 2
(d) - 2
Answer:
(b) 4

Question 4.
The line \(\frac{x-2}{3}=\frac{y-3}{4}=\frac{z-4}{5}\) is parallel to the plane
(a) 2x + 3y + 4z = 0
(b) 3x + 4y - 5z = 7
(c) 2x + y - 2z = 0
(d) x - y + z = 2
Answer:
(b) 3x + 4y - 5z = 7

Question 5.
The shortest distance of the point (a, b, c) from x-axis is:
(a) \(\sqrt{a^2+b^2}\)
(b) \(\sqrt{b^2+c^2}\)
(c) \(\sqrt{c^2+a^2}\)
(d) \(\sqrt{a^2+b^2+c^2}\)
Answer:
(b) \(\sqrt{b^2+c^2}\)

Question 6.
The angle between the line \(\frac{x+1}{2}=\frac{y-1}{1}=\frac{z-3}{-2}\) and the plane x + y + 1 = 0 is:
(a) 30°
(b) 60°
(c) 45°
(d) 120°
Answer:
(c) 45°

Question 7.
The angle between the straight line \(\frac{x-1}{2}=\frac{y+3}{-1}=\frac{z-5}{2}\) and the plane 4x - 2y + 4z = 9 IS:
(a) 60°
(b) 90°
(c) 45°
(d) 30°
Answer:
(b) 90°

Question 8.
The coordinates of the point of intersection of the line \(\frac{x-6}{-1}=\frac{y+1}{0}=\frac{z+3}{4}\) and the plane x + y - z = 3 are:
(a) (2, 1, 0)
(b) (7, - 1, - 7)
(c)(1, 2, - 6)
(d) (5, - 1, 1)
Answer:
(d) (5, - 1, 1)

Question 9.
The distance of the plane through (1, 1, 1) and perpendicular to the line \(\frac{x-1}{3}=\frac{y-1}{0}=\frac{z-1}{4}\) from the origin is:
(a) \(\frac{3}{4}\)
(b) \(\frac{4}{3}\)
(c) \(\frac{7}{5}\)
(d) 1
Answer:
(c) \(\frac{7}{5}\)

Question 10.
The direction ratios of the line which is perpendicular to the lines \(\frac{x-7}{2}=\frac{y+17}{-3}\) and x + 5 = \(\frac{y+3}{2} = \frac{z-4}{-2}\) are:
(a) (4, 5, 7)
(b) (4, -5, 7)
(c) (4, - 5, - 7)
(d) (- 4, 5, 7)
Answer:
(a) (4, 5, 7)

Question 11.
The angle between the plane 3x + 4y = 0 and the line x² + y² = 0is:
(a) 0°
(b) 30°
(c) 60°
(d) 90°
Answer:
(a) 0°

Question 12.
If the points (0, - 1, 2), (- 3, - 4, - 5), (- 6, - 7, - 8) and (x, x, x) are non-coplanar then x is:
(a) - 2
(b) 0
(c) 3
(d) any real number
Answer:
(d) any real number

Question 13.
The equation of the plane through the point (1, 2, -3) which is parallel to the plane 3x - 5y + 2z = 11 is given by:
(a) 3x - 5y + 2z - 13 = 0
(b) 5x - 3y + 2z + 13 = 0
(c) 3x - 2y + 5z + 13 = 0
(d) 3x - 5y + 2z + 13 = 0.
Answer:
(d) 3x - 5y + 2z + 13 = 0.

Question 14.
The distance between the parallel planes:
x + 2y - 3z and 2x + 4y - 6z + 7 = 0 is:
(a) \(\frac{2}{\sqrt{14}}\)
(b) \(\frac{11}{\sqrt{56}}\)
(c) \(\frac{7}{\sqrt{56}}\)
(d) none of these
Answer:
(b) \(\frac{11}{\sqrt{56}}\)

Question 15.
The angle between the planes 2x - y + z = 6 and x + y + 2z = 7 is:
(a) \(\frac{\pi}{4}\)
(b) \(\frac{\pi}{6}\)
(c) \(\frac{\pi}{3}\)
(d) \(\frac{\pi}{2}\)
Answer:
(c) \(\frac{\pi}{3}\)

Fill in the Blanks

Question 1.
The vector equation of a line which passes through the points (3, 4, - 7) and (1, - 1, 6) is ......................
Answer:
\(\vec{r}\) = 3î + 4ĵ - 7k̂ + λ(- 2î - 5ĵ + 13k̂)

Question 2.
The line of shortest distance between two skew lines is ......................... to both the lines.
Answer:
perpendicular

Question 3.
If a line lies in a plane, then normal to the plane is ........................ to the line.
Answer:
perpendicular

Question 4.
If two lines are parallel, then direction ratios are ........................
Answer:
proportional

Question 5.
The distance of the plane 2x - y + 2z + 1 = 0 from the origin is ....................
Answer:
\(\frac{1}{3}\) unit

True/False

Question 1.
A given line in space can be extended in two opposite directions and so it has two sets of direction cosines.
Answer:
True

Question 2.
Any two sets of direction cosines of a line are also proportional.
Answer:
False

Question 3.
A line is uniquely determined if it passes through a given point and has given direction.
Answer:
True

Question 4.
For skew lines, the line of the shortest distance will be perpendicular to both the lines.
Answer:
True

Question 5.
ax + by + cz = d is the vector equation of the plane, where a, b and c are the direction cosines of the normal to the plane.
Answer:
False