RBSE Class 12 Maths Important Questions Chapter 1 संबंध एवं फलन

Rajasthan Board RBSE Class 12 Maths Important Questions Chapter 1 संबंध एवं फलन Important Questions and Answers.

RBSE Class 12 Maths Chapter 1 Important Questions संबंध एवं फलन

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
यदि A = {1, 2, 3} पर एक सम्बन्ध र परिभाषित है, तब
R है R = {(1, 1), (2, 2). (3, 3), (1, 2), (2, 3), (1, 3)}
(A) स्वतुल्य परन्तु सममित नहीं
(B) स्वतुल्य परन्तु संक्रामक नहीं
(C) सममित तथा संक्रामक
(D) न सममित न स्वतुल्य
हल:
(A) स्वतुल्य परन्तु सममित नहीं

क्योंकि (1, 1), (2, 2), (3, 3) ∈ R ⇒ R स्वतुल्य है। परन्तु R सममित नहीं है क्योंकि (1, 2) ∈ R परन्तु (2, 1) ∉ R

प्रश्न 2.
प्राकृत संख्याओं के समुच्चय N में एक सम्बन्ध र इस प्रकार परिभाषित है कि m Rn ⇔ m, n का भाजक, ∀ m, n, ∈ N, तब R है
(A) स्वतुल्य एवं सममित
(B) सममित एवं संक्रामक
(C) तुल्यता सम्बन्ध
(D) स्वतुल्य एवं संक्रामक
हल:
(D) स्वतुल्य एवं संक्रामक

क्योंकि प्रत्येक संख्या स्वयं की भाजक होती है। यहाँ पर m, n का भाजक है। लेकिन यह n, m का भाजक नहीं हो सकता है, अतः सम्बन्ध सममित नहीं है। माना x₁, x₂, x₃, ∈ N यदि x₁, x₂, का भाजक है और x₂, x₃, का भाजक है तो x₁, x₂, का भाजक होगा। सम्बन्ध संक्रामक है। अतः सम्बन्ध स्वतुल्य एवं संक्रामक होगा। सही विकल्प (D) है।

प्रश्न 3.
यदि A = {a, b, c, d} में एक सम्बन्ध = {(a, b), (b, a), (a, a)} निम्न तरह से परिभाषित है तब R है
(A) सममित तथा संक्रामक
(B) स्वतुल्य एवं संक्रामक
(C) केवल सममित
(D) केवल संक्रामक
हल:
(A) यह सम्बन्ध सममित तथा संक्रामक है।

परन्तु स्वतुल्य नहीं है क्योंकि b, C ∈ A परन्तु (b, b) ∉ R तथा (c, c) ∉ R

प्रश्न 4.
वास्तविक संख्याओं के समुच्चय में "x, y से छोटा है" होगा
(A) स्वतुल्य तथा संक्रामक
(B) सममित तथा संक्रामक
(C) केवल संक्रामक
(D) स्वतुल्य तथा प्रतिसममित
हल:
(C) यह सम्बन्ध केवल संक्रामक है।
यदि "x, y से छोटा अथवा बराबर है" सम्बन्ध होता तब यह सम्बन्ध स्वतुल्य और प्रतिसममित भी होता।

प्रश्न 5.
यदि f(x) = \(\frac{x}{1-x}=\frac{1}{y}\) तो f(y) का मान होगा
(A) x
(B) x -1
(C) +1
(D) \(\left(\frac{1-x}{2 x-1}\right)\)
हल:
(D) \(\left(\frac{1-x}{2 x-1}\right)\)

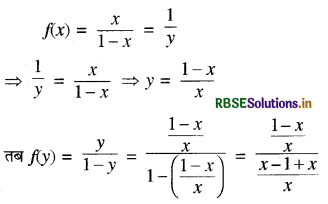
= \(\frac{1-x}{2 x-1}\) अतः सही विकल्प (D) है।

प्रश्न 6.
यदि f(x) = 2 |x - 2| -3 |x - 3| हो तो 2 < x < 3 के लिए f(x) बराबर है
(A) 5 - x
(B) x - 5
(C) 5x - 13
(D) 5 + x
हल:
(C) 5x - 13
f(x) = 2|x - 2| - 3|x - 3|
= 2{(x - 2)} - 3 {-(x - 3)}
= 2x - 4 + 3x - 9 = 5x - 13
सही विकल्प (C) है।

प्रश्न 7.
निम्न में से कौनसा फलन एकैकी है
(A) f : R → R, f(x) = x²
(B) f: R → R, f(x) = x + 1
(C) f : R → R, f(x) = e^x + e^x
(D) f : R → R, f(x) = 3x²
हल:
(B) f : R → R, f(x) = x + 1

माना x₁, x₂, ∈ R (प्रान्त) इस तरह से है कि
f(x₁) = f(x₂) =
⇒ x₁ + 1 = x₂ + 1
⇒ x₁ = x₂
अतः f(x₁) = f(x₂)
⇒ x₁ = x₂, x₁, x₂, ∈ R
∴ f एकैकी फलन है।

प्रश्न 8.
R से R में परिभाषित निम्न में से कौनसा फलन एकैकी है
(A) f(x) = |x|
(B) f(x) = cos x
(C) f(x) = e^x
(D) f(x) = x²
हल:
(C) f(x) = e^x x₁, x₂, ∈ R इस तरह से
f(x₁) = f(x₂)
⇒ e^x₁ = e^x₂
⇒ log_e e^x₁ = log_e e^x₂
⇒ x₁ log_ee = x₂ log_ee
x₁ = x₂ [∵ log_ee = 1]
अतः f(x₁) = f(x₂)
⇒ x₁, = x₂, ∀ x₁, x₂, E R
∴ f एकैकी फलन है।

प्रश्न 9.
निम्न में से कौन-सा फलन आच्छादक है
(A) f: Z →Z, f(x) = |x|
(B) f : N → N, f(x) = |x|
(C) f: R → R⁺, f(x) = |x|
(D) f : C → R, f(x) = |x|
हल- (C) f : R → R⁺, f(x) = x
∴ प्रत्येक धनात्मक वास्तविक संख्या का पूर्व प्रतिबिम्ब प्रान्त R. में विद्यमान है।

प्रश्न 10.
R से R में परिभाषित निम्न में से कौनसा फलन आच्छादक
(A) f(x) = x
(B) fix) = e^-x
(C) fix) = x³
(D) f(x) = sin x
हल:
(C) f(x) = x³
यहाँ f : R → R तथा f(x) = x³ माना y ∈ R सहप्रान्त यदि सम्भव हो तो माना y का पूर्व । प्रतिबिम्ब प्रान्त R में x है।
तब f(x) = y
⇒ y = x³ ∴ x = (y)^1/3 ∈ R ∀ y ∈ R अतःy के प्रत्येक मान का पूर्व प्रतिबिम्ब प्रान्त R में विद्यमान है।
अतः f आच्छादक फलन है।

प्रश्न 11.
यदि f : R → R, f(x) = 2x - 1 तथा g : R → R, g(x) = x² तब (gof) (x)
(A) 2x² – 1
(B) (2x - 1)²
(C) x² - 2x - 1
(D) 4x² - 2x + 1
हल:
(B) (2x - 1)²

f: R → R, f(x) = 2x - 1 तथा g : R → R, g(x) = x²
तब (gof)(x) = g[f(x)] = g(2x – 1) .
= (2x - 1)²

प्रश्न 12.
यदि f : R → R, f(x) = sin x तथा g : R → R, g (x) = x तब (fog) (x) =
(A) sin x²
(B) sin x
(C) sin x + x²
(D) sin² x²
हल:
(A) sin x²
f(x) = sin x
g(x) = x²
तब (fog)(x) = g(x)]
= f(x²)
= sin x²
अतः सही विकल्प (A) है।

प्रश्न 13.
यदि f(x) = \(\frac{1-x}{1+x}\) (x ≠ - 1), तब f^-1(x)
(A) -f(x)
(B) f(x)
(C) \(\frac{1}{f(x)}\)
(D) \(\frac{1}{-f(x)}\)
हल:
(B) यदि के अन्तर्गत x का प्रतिबिम्ब y हो तो " निम्न प्रकार परिभाषित होगा
f^-1(y) = x = f(x) = y
y = \(\frac{1-x}{1+x}\)
⇒ 1 - x = y + xy
⇒ x = \(\frac{1-y}{1+y}\) ⇒ f^-1(y) = \(\frac{1-y}{1+y}\)
⇒ f^-1(x) = \(\frac{1-x}{1+x}\) = f(x)

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
सरल रेखाओं के समुच्चय में x R y ⇔ x ⊥ y से परिभाषित सम्बन्ध क्या सममित है ? यदि है, तो क्यों? कारण भी लिखिये।
उत्तर:
हाँ, क्योंकि यदि x ⊥ y है तो y x अवश्य ही होगा, इसलिए x R y है तो y R x भी यहाँ पर है। इसलिए सम्बन्ध सममित है।

प्रश्न 2.
क्या संक्रामक सम्बन्ध में x R y, y R z ⇔ x R z सत्य कथन है?
उत्तर:
हाँ।

प्रश्न 3.
क्या त्रिभुजों के किसी समुच्चय में 'सर्वांगसम' सम्बन्ध स्वतुल्य है?
उत्तर:
हाँ, क्योंकि प्रत्येक त्रिभुज स्वयं के सर्वांगसम होता है।

प्रश्न 4.
यदि A = {1, 2, 3} तो A में परिभाषित किये जाने वाले सभी सम्भव अरिक्त सम्बन्धों की संख्या कितनी होगी?
उत्तर:
A = {1, 2, 3}
A में अवयवों की संख्या = 3
ब A × A में अवयवों की संख्या = 3 × 3 = 3² = 9
अतः A में परिभाषित अरिक्त सम्बन्धों की अभीष्ट संख्या
= 2⁹ - 1 = 512 - 1 = 511

प्रश्न 5.
यदि किसी समतल में स्थित सरल रेखाओं के समुच्चय A में एक सम्बन्ध R इस प्रकार परिभाषित है कि x R y ⇔ x, y के समान्तर है तो R में कौन-कौन से सम्बन्ध होंगे?
उत्तर:
R स्वतुल्य होगा क्योंकि प्रत्येक रेखा स्वयं के समान्तर होती है।
R सममित होगा क्योंकि x, y के समान्तर हो तो y भी x के समान्तर होगी। R संक्रामक भी होगा क्योंकि x ∥ y, y ∥ z x ∥z ही होगा।

प्रश्न 6.
समुच्चयों के किसी समुच्चय S में एक सम्बन्ध R इस प्रकार परिभाषित है कि A R B ⇔ A, B का उपसमुच्चय है तो क्या सम्बन्ध र प्रतिसममित होगा?
उत्तर:
R सम्बन्ध प्रति सममित होगा क्योंकि किन्हीं दो समुच्चयों A व B के लिए A ⊆ B तथा B ⊆ A ⇒ A = B

प्रश्न 7.
पूर्णांकों के समुच्चय I में यदि एक सम्बन्ध र इस प्रकार परिभाषित हो कि x R y ⇔ x > y तो क्या R एक संक्रामक सम्बन्ध है? यदि हाँ, तो क्यों?
उत्तर:
R एक संक्रामक सम्बन्ध है क्योंकि x, y, z ∈ I तथा x >y
तथा y > z तब x > y > z से x > अर्थात् (x, y) ∈ R,
(y, z) ∈ R = (x, z) ∈ R Vx, y, z ∈ I

प्रश्न 8.
क्या ऐसे सम्बन्ध हो सकते हैं जो सममित के साथ प्रति सममित भी हों?
उत्तर:
हाँ। प्राकृत संख्याओं के समुच्चय में “=” (बराबर) सम्बन्ध सममित भी है तथा प्रति सममित भी।

प्रश्न 9.
क्या f : z → z, f(x) = x² एकैकी फलन है?
उत्तर:
नहीं, f : z → z f(x) = x² एकैकी फलन नहीं है क्योंकि 3.
-3 ∈ Z ऐसे अवयव हैं कि 3 ≠ -3 लेकिन f(-3) = f(3) = 9
अर्थात् - 3 तथा 3 का एक प्रतिबिम्ब 9 है।

प्रश्न 10.
क्या f: R → R, f(x) = sin x एक बहु एकैकी फलन है?
उत्तर:
f: R → R, f(x) = sin x एक बहु एकैकी फलन है क्योंकि sin x एक आवर्ती फलन है अर्थात् एक से अधिक कोणों के लिये sin x का मान समान हो सकता है।

प्रश्न 11.
क्या f: z → Z, f(x) = x + 5 आच्छादक फलन है?
उत्तर:
हाँ, यहाँ पर , आच्छादक फलन है। क्योंकि f(Z) = f(Z) अर्थात् f का परिसर = सहप्रान्त

प्रश्न 12.
यदि A = {-1, 1, -2, 2, 3}, B = {1, 4, 6, 9} तथा f: A → B, f(x) = x² द्वारा परिभाषित हो तो f^-1(4) तथा f^-1(9) का मान ज्ञात कीजिये।
हल:
माना f^-1(4) = x
= f(x) = 4
= x² = 4 ∴ x = + 2
f^-1(4) = {-2, 2}
माना f^-1(9) = x Df(x) = 9
⇒ x² = 9 ∴ x = + 3
∴ f^-1(9) = {3} [∵ - 3 4 A]

प्रश्न 13.
यदि f : R → R, f(x) = 2x + 1, g : R → R, f(x) = x³ हो तो (fog)^-1(17) का मान ज्ञात कीजिये।
हल:
माना (fog)^-1(17) = x
⇒ (fog)(x) = 17
⇒ f[g(x)] = 17
⇒ f(x) = 17 = 2x³ + 1 = 17
⇒ 2x³ = 16 = x = 8
⇒ x = (8)^1/3 = 2

प्रश्न 14.
सदिशों का योग एक साहचर्य संक्रिया है, क्यों?
हल:
हम जानते हैं कि किन्हीं तीन सदिशों \(\vec{a}, \vec{b}\) व \(\vec{c}\) के लिये \(\vec{a}+(\vec{b}+\vec{c})=(\vec{a}+\vec{b})+\vec{c}\) होता है।

प्रश्न 15.
यदि A = {1, -1} हो तो बताइये कि गुणन A पर एक द्विचर संक्रिया है या नहीं?
हल:
दिये गये समुच्चय
A = {1, - 1} गुणन A पर द्विचर संक्रिया है क्योंकि
1 × 1 = 1 ∈ A
(1) × (-1) = -1 ∈ A
(-1) × (-1) = 1 ∈ A

प्रश्न 16.
वास्तविक संख्याओं के समुच्चय R पर यदि एक द्विचर संक्रिया * निम्न प्रकार परिभाषित हो तो।
a * b = a + 3b ∀ a, b ∈ R यह संक्रिया साहचर्य है या नहीं?
(a * b) * c = (a + 3b) * c
= a + 3b + 3c
तथा a * (b * c)= a * (b + 3c)
= a + 3(b + 3c)
= a + 3b + 9c
∵ a * (b * c) ≠ (a * b) * C .
अतः स्पष्ट है कि यह संक्रिया साहचर्य नहीं है।

प्रश्न 17.
वास्तविक संख्याओं के समुच्चय R में प्रत्येक a ∈ R के लिये (-a) ∈ R योग संक्रिया के लिये क्या प्रतिलोम अवयव है?
हल:
हाँ, क्योंकि a + (-a) = (-a) + a = 0 (तत्समक) अतः R का प्रत्येक अवयव योग संक्रिया के लिये व्युत्क्रमणीय है।

प्रश्न 18.
क्या वास्तविक संख्याओं के समुच्चय R में 0 तथा 1 क्रमशः योग एवं गुणन संक्रियाओं के लिये तत्समक अवयव हैं?
उत्तर:
हाँ, क्योंकि a ∈ R के लिये 0 + a = a + 0 तथा 1.a = a.1 = a

लघूत्तरात्मक प्रश्न

प्रश्न 1.
यदि एक सम्बन्ध र समुच्चय A में परिभाषित है, तो सिद्ध कीजिये R सममित होगा यदि और केवल यदि R = R^-1
हल:
हमें यहाँ पर सिद्ध करना होगा कि
(i) यदि R सममित है तो R = R^-1 होगा, और
(ii) यदि R = R^-1 है तो R सममित होगा।
(i) माना (x, y) ∈ R, तब
(x, y) ∈ R = (y, x) ∈ R {∵ R सममित है}
(x, y) ∈ R^-1 (परिभाषा से) R ⊂ R^-1 ....(1)
(y, x) ∈ R^-1 ⇒ (x, y) ∈ R परिभाषा से
(y, x) ∈ R. ∵ R सममित है ।
R^-1 ⊂ R ....(2) समी. (1) तथा (2) से R = R-1 (ii) मान लो (x, y) ER तब (x, y) ER = (y, x) ER-1 [परिभाषा से]
= (y, x) ∈ R . [:: R^-1 = R]
∴ R सममित सम्बन्ध है।
अतः R सममित सम्बन्ध है यदि और केवल यदि
R = R^-1

प्रश्न 2.
यदि f : A → B एक एकैकी आच्छादक फलन हो, तो सिद्ध कीजिए कि
(f^-1)^-1 = f
हल:
f : A → B, एक एकैकी आच्छादक फलन है।
∴ इसका प्रतिलोम फलन f^-1 : B → A विद्यमान होगा और f^-1 भी एकैकी. आच्छादक होगा।
माना कि f^-1 = g
तो (f^-1)^-1 = g^-1 .......(1)
पुनः माना कि g^-1(x) = y .... (2)
तो x = g(y) ⇒ x = f^-1(y) ⇒ f(x) = y
⇒ f(x) = g^-1(x) [समीकरण (2) से]
⇒ f = g^-1 ⇒ f = (f^-1)^-1 [समीकरण (1) से]

प्रश्न 3.
यदि g(x) = x² + x - 2 तथा (gof) (x) = 4x² - 10x + 4 हो, तो f(x) की गणना कीजिए।
हल:
दिया है
g(x) = x² + x - 2 .... (1)
(gof) (x) = g[(x)]
4x² - 10x + 4 = g[f(x)]
4x² - 10x + 4 = g(y)
4x² - 10x + 4 = y² + y - 2
⇒ y² + y + (10x - 4x² - 6) = 0
या y = \(\frac{-1 \pm \sqrt{1-4\left(10 x-4 x^2-6\right)}}{2.1}\)
या f(x) = \(\frac{-1 \pm \sqrt{16 x^2-40 x+25}}{2}\)
या f(x) = \(\frac{-1 \pm(4 x-5)}{2}\)
या f(x) = 2x - 3
या f(x) = 2 - 2x

प्रश्न 4.
यदि f, g, h तीन फलन R से R पर इस प्रकार परिभाषित हैं कि (x) = x², g(x) = cos x एवं h(x) = 2x + 3, तो [ho (gof) (√2π) का मान लिखिए।
हल:
चूंकि f : R → R तथा g : R → R
∴ gof : R → R . तथा h : R → R
ho (gof) : R → R होगा।
अब {ho (go)} (2π)
= h[ (gof) (√2π)]
= h[g{5 (√2π)}]]
= h [g (2π)] [f की परिभाषा से]
= h [cos 2π] [g की परिभाषा से]
= h [1] = 2 . 1 + 3 [h की परिभाषा से]
= 2 + 3 = 5

प्रश्न 5.
यदि f:A → B एकैकी आच्छादक फलन हो तो g : B → A, f का प्रतिलोम फलन हो, तो fog = I_B और gof = I_A जहाँ I_A और I_B क्रमशः A और B के तत्समक फलन हैं।
हल:

∵ f : A → B और g : B → A
∴ fog : B → B और gof : A → A होंगे।
अब प्रत्येक a ∈ A के लिए, एक अद्वितीय b ∈ B जहाँ f(a) = b
या g(b) = a .... (1)
अतः (fog) (b) = f{g(b)}
= f(a) समीकरण (1) से
= b समीकरण (1) से
(fog) (b) = b, ∀ b ∈ B = fog = I_B

इसी प्रकार (gof) (a) = g[f(a)]
= g(b) [समीकरण (1) से]
= a
∴ (gof) (a) = a ∀ a ∈ A = gof = I_A

प्रश्न 6.
सिद्ध कीजिए कि समुच्चय 2 में परिभाषित संबंध R, aRb ⇔ a - b, 3 से विभाज्य है, एक तुल्यता संबंध है।
हल:
R स्वतुल्य है, क्योंकि समस्त a ∈ z के लिये 3, (a - a) को । विभाजित करता है। अतः (a, a) ∈ R पुनः यदि (a, b) ∈ R, तो 3, a - b को विभाजित करता है। अतएव b - a को भी 3 विभाजित करता है। अतः (b, a) ∈ R, जिससे सिद्ध होता है कि R सममित है। इसी प्रकार यदि (a, b) ∈ R तथा (b, c) ∈ R, तो a - b तथा b - c संख्या 3 से भाज्य है अब a - c = a - b + b - c सम (even) है। चूँकि समसंख्या को समसंख्या में जोड़ने पर समसंख्या प्राप्त होती है और विषम संख्या को विषम संख्या में जोड़ने पर समसंख्या प्राप्त होती है अतः (a - c) भी 3 से भाज्य है। इससे सिद्ध होता है कि R संक्रामक है। अतः दिया गया सम्बन्ध स्वतुल्य, सममित तथा संक्रामक है अतः समुच्चय z में R एक तुल्यता संबंध है।

प्रश्न 7.
यदि f,g : R → R फलन इस प्रकार परिभाषित है कि f(x) = x² + 1,g (x) = 2x - 3 तो fog (x),g of (x) तथा gog (3) ज्ञात कीजिए।
हल:
दिया गया है
f(x) = x² + 1, g(x) = 2x - 3
ज्ञात करना है- fog (x), g of (x) तथा g08 (3)
fog (x) =f (g(x)) = f (2x - 3) = (2x - 3)² + 1
= 4x² - 12x + 9 + 1
= 4x² - 12x + 10
gof (x) = 8 (f(x)) = g (x² + 1) = 2 (x² + 1) - 3
g of (x) = 2x² + 2 - 3 = 2x² - 1
gog (3) = g (g(3)) = g. (2 x 3 - 3) = g (3)
∴ g08 (3) = 2 × 3 - 3 = 6 - 3 = 3

निबन्धात्मक प्रश्न

प्रश्न 1.
समुच्चय I × I₀ में सम्बन्ध र निम्न प्रकार से परिभाषित है
(a, b) R (c,d) ad = bc
यदि I₀, अशून्य पूर्णांकों का समुच्चय हो, तो सिद्ध कीजिये कि R तुल्यता सम्बन्ध है।
हल:
समुच्चय I x I₀ में सम्बन्ध R को तुल्यता सम्बन्ध सिद्ध करने के लिये हमें R को
(i) स्वतुल्य
(ii) सममित
(iii) संक्रामक सिद्ध करना होगा।

(i) स्वतुल्य-माना कि (a, b) ∈ I × I₀, तब
(a, b) ∈ I × I₀ ⇒ a ∈ I, b ∈ I₀
⇒ ab = ba(क्रमविनिमेय नियम से)
⇒ (a, b) R (a, b)
∴ R एक स्वतुल्य सम्बन्ध है।

(ii) सममित-माना कि (a, b) R (c, d) तब
(a, b) R (c, d) ⇒ ad = bc
⇒ bc = ad
⇒ cb = da (क्रमविनिमेय नियम से)
⇒ (c, d) R (a, b)
∴ R एक सममित सम्बन्ध है।

(iii) संक्रामक-माना कि (a, b) R (c, d) तथा
(c, d) R (e, f), तब
(a, b) R (c, d) ⇒ ad. = bc
तथा (c, d) R (e, f) ⇒ cf = de
(a, b) R (c, d) तथा (c, d) R (e, f)

गुणा करने पर =
⇒ (ad) (cf) = (bc) (de)
⇒ af = bc
⇒ (a, b) R (c, f)
∴ R एक संक्रामक सम्बन्ध है।
अतः समुच्चय I × I₀ में R एक तुल्यता सम्बन्ध है।

प्रश्न 2.
वास्तविक संख्याओं के समुच्चय में एक सम्बन्ध R₁ निम्न प्रकार परिभाषित है
(a, b) ∈ R₁ = 1 + a.b > 0 ∀ a, b ∈ R सिद्ध कीजियें कि R₁ स्वतुल्य एवं सममित है परन्तु संक्रामक नहीं है।
हल:
दिया गया है
R = वास्तविक संख्याओं का समुच्चय R में एक सम्बन्ध R₁ निम्न प्रकार परिभाषित है
(a, b) ∈ R₁ 0 1 + ab > 0 ∀ a, b ∈ R
(i) स्वतुल्य-माना a ∈ R ⇒ 1 + a.a = 1 + a² > 0
[∵ a² > 0]
⇒ aR₁a, ∀ a ∈ R
∴ R₁ एक स्वतुल्य सम्बन्ध है।

(ii) सममित-माना कि a R₁ b, तब
a R₁ b ⇒ 1 + ab > 0 (∵ ab = ba,)
⇒ 1 + b a > 0 ∀ a,b ∈ R)
⇒ bR₁a
R₁ एक सममित सम्बन्ध है।

(iii) संक्रामक-माना कि aRb तथा bR₁C, तब aRb तथा bR₁c = 1 + ab > 0 तथा 1 + bc > 0.
यदि हम a = 1, b = \(\frac{1}{2}\) तथा c = - 1 लें, तो

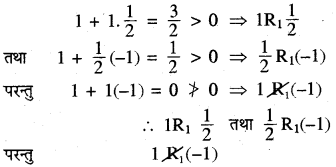
अतः R संक्रामक सम्बन्ध नहीं है।

प्रश्न 3.
यदि f: R→R; f(x) = 3x + 2 तथाg : R→R,g(x) = 4x हो तो निम्न का सत्यापन कीजिए
(gof)^-1 = f^-1og^-1
हल:
स्पष्टतः f तथा g एकैकी आच्छादक फलन हैं। अतः इनके प्रतिलोम f^-1 तथा g^-1 विद्यमान हैं।
तथा f^-1 : R → R, f^-1(x) = \(\frac{x-2}{3}\), ∀ x ∈ R
g^-1 : R → R, g^-1 (x) = \(\frac{x}{4}\) ∀ x ∈ R

पुनः दो एकैकी आच्छादक फलनों का संयुक्त फलन भी एकैकी आच्छादक होता है।
:. (gof) : R → R भी एकैकी आच्छादक है।

फलतः इसका प्रतिलोम फलन विद्यमान है।
तथा (gof)-1 : R → R अब
(gof) x = g [f(x)] = g [3x + 2]
= 4 (3x + 2) = 12x + 8
∴ (gof)^-1(x) = \(\frac{x-8}{12}\) ............(1)

पुनः (f^-1og^-1) : R → R

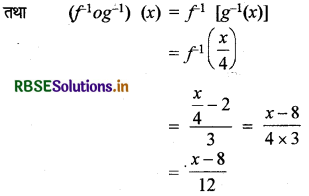
समीकरण (1) तथा (2) से
(gof)^-1(x) = (f^-1og^-1) (x), H XER
(gof)^-1 = f^-1og^-1

प्रश्न 4.
वास्तविक संख्याओं के समुच्चय R में एक संक्रिया * निम्न प्रकार परिभाषित है :
a * b = a + b + ab, a, b ∈ R
(i) * की क्रमविनिमेयता तथा साहचर्य की जाँच कीजिये।
(ii) * का तत्समक अवयव, यदि विद्यमान हो, ज्ञात कीजिये।
(iii) * के सापेक्ष R के व्युत्क्रमणीय अवयवों को ज्ञात कीजिये।
हल:
(i) यदि a, b ∈ R तब परिभाषा से
a * b = a + b + ab = b + a + b.a
= b * a
(वास्तविक संख्याओं के योग और गुणन की क्रमविनिमेयता से)
∴ * एक क्रमविनिमेय संक्रिया है। पुनः a * (b * c) = a * (b + C + bc)
= a + (b + c + bc) + a (b + c + bc)
= a + b + c + ab + bc + ca + abc ....(1)
तथा (a * b) * c = (a + b + ab) * c
a + b + ab+ C + (a + b + ab)c
= a + b + c + ab + bc + ac + abc ....(2)
समी.(1) तथा (2) से
a * (b * c) = (a * b) * C, ∀ a, b, c ∈ R
∴ * एक साहचर्य संक्रिया है।

(ii) यदि सम्भव हो तो माना * का तत्समक अवयव e हो तब किसी a ∈ R के लिये
a * e = a तत्समक की परिभाषा से
⇒ a + e + ae = a
⇒ e (1 + a) = 0
⇒ e = 0
[∵ (1 + a) का मान शून्य होना आवश्यक नहीं है।]
∴ 0, * का तत्समक अवयव है।

(iii) माना a ∈ R यदि सम्भव हो तो माना कि a का प्रतिलोम x अवयव है। तब परिभाषा के अनुसार
a * x = 0 [∵ 0, तत्समक है]
⇒ a + x + ax = 0
⇒ a + x (1 + a) = 0
⇒ x = \(\frac{-a}{1+a}\) ∈ R.
यदि a ≠ - 1
∴ a ∈ R (a + - 1) व्युत्क्रमणीय है।

प्रश्न 5.
वास्तविक संख्याओं के समुच्चय R में एक संक्रिया * निम्न प्रकार परिभाषित है:
a * b = a + b - ab, ∀ a, b ∈ R
(i) * की क्रमविनिमेयता तथा साहचर्य की जाँच कीजिये।
(ii) * का तत्समक अवयव, यदि विद्यमान हो, ज्ञात कीजिये।
(iii) * के सापेक्ष R के व्युत्क्रमणीय अवयवों को ज्ञात कीजिये।
हल:
(i) a, b ∈ R = a * b = a + b - ab .
b + a - ba
= b * a
अतः a * b = b * a
⇒ * एक क्रमविनिमेयता संक्रिया है।
पुनः a * (b * c) = a * (b + c - bc)
a + b + c - bc - a (b + c - bc)
= a + b + C - bc - ab-ac + abc a + b + c - ab - bc - ac + abc ....(1)

तथा (a * b) * c = (a + b - ab) * c
= a + b - ab + c - (a + b - ab) c a + b + c - ab - ac - be + abc
= a + b + c - ab - bc - ac + abc ....(2)
समीकरण (1) तथा (2) से
a * (b * c) = (a * b) * c
∴ * एक साहचर्य संक्रिया है।

(ii) यदि सम्भव हो तो माना * का तत्समक अवयव e हो तब किसी a ∈ R के लिए,
a * e = a (तत्समक की परिभाषा से)
⇒ a + e - ae = a . e(1 - a) = 0
e = 0 ∈ R [∵ (1 - a) का मान सदा शून्य होना आवश्यक नहीं है।]
* का तत्समक अवयव 0 है।

(iii) माना a ∈ R के लिए यदि सम्भव हो तो माना a का प्रतिलोम अवयव x है।
⇒ a * x = 0
⇒ a + x - ax = 0
⇒ ax - x = a
⇒ x(a - 1) = a
∴ x = \(\frac{a}{a-1}\) ∈ R यदि a ≠ 1
अर्थात् a ∈ R (a ≠ 1) व्युत्क्रमणीय है।

प्रश्न 6.
धनात्मक परिमेय संख्याओं के समुच्चय Q⁺ पर निम्न दो संक्रियायें परिभाषित की गई हैं :
a * b = ab, ∀ a, b ∈ Q⁺
सिद्ध कीजिये कि दोनों संक्रियाएँ क्रमविनिमेय तथा संक्रामक हैं। उनके तत्समक अवयव ज्ञात कीजिये तथा इन संक्रियाओं के सापेक्ष के अवयव का प्रतिलोम अवयव भी ज्ञात कीजिये।
हल:
धनात्मक परिमेय संख्याओं के समुच्चय Q⁺ में
a * b = \(\frac{ab}{3}\), ∀ a, b ∈ Q

क्रमविनिमेय: a * b = \(\frac{a b}{3}=\frac{b a}{3}\) = b* a
∴ * क्रमविनिमेय संक्रिया है।

साहचर्य : (a * b) * c = \(\frac{ab}{3}\) * c = \(\frac{a b c}{3 \times 3}=\frac{a b c}{9}\)
(a * b) * c = a * \(\frac{b c}{3}=\frac{a b c}{3 \times 3}=\frac{a b c}{9}\)
⇒ (a * b) * c = a * (b * c)
∴ * साहचर्य संक्रिया है।।
माना * संक्रिया के लिए तत्समक अवयव e है।
⇒ a * e = a
⇒ \(\frac{ae}{3}\) = a
⇒ e = 3
पुनः माना a ∈ Q⁺ में यदि सम्भव हो तो माना a का प्रतिलोम अवयव x है।
∴ a * x = 3 (तत्समक अवयव)
⇒ \(\frac{a x}{3}\) = 3 ⇒ x = \(\frac{9}{a}\)
∴ a ∈ Q⁺ व्युत्क्रमणीय है, ∴ प्रतिलोम अवयव \(\frac{9}{a}\) है।

प्रश्न 7.
यदि पूर्णांकों के समुच्चय z में एक द्विचर संक्रिया * इस प्रकार से परिभाषित है कि a * b = a + b + 1, ∀ a, b ∈ z तो सिद्ध कीजिये कि द्विचर संक्रिया * क्रमविनिमेय व साहचर्य है।
हल:
पूर्णांकों के समुच्चय z में । a * b = a + b + 1, ∀ a, b ∈ z
क्रमविनिमेय : a * b = a + b + 1 - a * b = b + a + 1 = b * a [z में योग संक्रिया क्रमविनिमेय है।]
⇒ a * b = b * a.
∴ * संक्रिया क्रमविनिमेय है।
साहचर्य :(a * b) * c = (a + b + 1) * C
= a + b + 1 + c + 1
= a + b + C + 2 ....(1)
पुनः a * (b * c) = a * (b + C + 1)
= a + b + C + 1 + 1
= a + b + C + 2 ....(2)
समी. (1) तथा (2) से
(a * b) * c = a * (b * c)
∴* संक्रिया साहचर्य है।

प्रश्न 8.
यदि फलन f : R → R,f (x) = x² + 2 तथा g : R→ R, g(x) = \(\frac{x}{x-1}\), x ≠ 1 द्वारा प्रदत्त है, तो fog तथा gof ज्ञात कीजिए और अतः (fog) (2) तथा (gof) (-3) ज्ञात कीजिए।
हल:

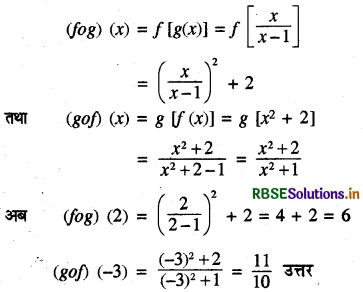
प्रश्न 9.
धनात्मक परिमेय संख्याओं के समुच्चय Q⁺ में निम्नलिखित प्रकार से परिभाषित * एक द्विआधारी संक्रिया है :
a*b = \(\frac{ab}{4}\)
सिद्ध कीजिए कि * क्रमविनिमेय तथा साहचर्य है। Q⁺ में * का प्रतिलोम अवयव यदि कोई है तो ज्ञात कीजिए।
हल:
a*b = \(\frac{a b}{4}=\frac{b a}{4}\) = b*a
अत: * क्रमविनिमेय है।

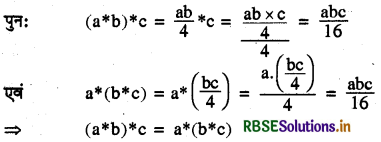
अतः * साहचर्य है।

प्रश्न 10.
निर्धारित कीजिए कि क्या सभी वास्तविक संख्याओं के समुच्चय R में R = {(a, b) : a, b ∈ R तथा a - b + √3 ∈ S, जहाँ सभी अपरिमेय संख्याओं का समुच्चय है, द्वारा परिभाषित सम्बन्ध र स्वतुल्य, सममित तथा संक्रामक है
हल:
यहाँ पर सम्बन्ध R, समुच्चय R पर इस प्रकार परिभाषित है कि
R = {(a, b) : a, b ∈ R तथा a – b + √3 S}
स्वतुल्यता-माना a ∈ R (वास्तविक संख्याओं का समुच्चय) अब, (a, a) ∈ R तब a - a + √3 = √3 ∈ S
इसलिये R स्वतुल्य है। ....(i)

सममित-माना a, b ∈ R (वास्तविक संख्याओं का समुच्चय)
माना a, b ∈ R = a - b √3 ∈ S (अपरिमेय संख्याओं का समुच्चय)
= b - a + 3 ∈ s
= (b, a) ∈ R
इसलिये R सममित सम्बन्ध है। . ....(ii)

संक्रामक-माना a, b, c ∈ R अब (a, b) ∈ R और (b, c) ∈ R
= a - b + √3 ∈ S और b - c + √3 ∈ S
= a - b + √3 + b - c + √3 ∈ S
= (a, c) ∈ R . इसलिये सम्बन्ध र संक्रामक है। ....(iii)
समीकरण (i), (ii) तथा (iii) से स्पष्ट है कि सम्बन्ध R स्वतुल्य, सममित तथा संक्रामक है।

प्रश्न 11.
माना कि A = R × R है तथा A में (a, b) * (c, a) = (a + c, b + d) द्वारा परिभाषित एक द्विआधारी संक्रिया है। सिद्ध कीजिये कि * क्रमविनिमेय तथा साहचर्य है। A में * का तत्समक अवयव ज्ञात कीजिये तथा अवयव (3, -5) का A में प्रतिलोम अवयव भी लिखिये।
हल:
क्रमविनिमेय
माना (a, b), (c, a) ∈ R × R
अब, (a, b) * (c, a) = (a + c, b + a)
= (c + a, d + b) (सम्बन्ध R, * के लिये क्रमविनिमेय रखता है)
= (c, a) * (a, b)
इसलिये * क्रमविनिमेय है।

साहचर्य
माना (a, b), (c, d), (e, f) ∈ R × R
अब, {(a, b) * (c, a)} * (e, f)
= (a + c, b + d) * (e, f)
= (a + c + e, b + d + )...(i)
और भी (a, b) * {(c, a) * (e, "} .
= (a, b) * {c + e, d+ f}
= (a + c + e, b + d + f...(ii)
समीकरण (i) और (ii) से हमें प्राप्त होता है ((a, b) * (c, a)) * (e, ) = (a, b) * ((c, a) * (e, 1)
इसलिये * साहचर्य है तत्समक का अस्तित्वमाना * के लिये (e, f) तत्समक अवयव R × R में है।
(a, b) * (e, f) = (a, b) = (e, f) * (a, b)
⇒ (a + e, b + f) = (a, b) = (e + a, f + b)
⇒ a + e = a तथा b + f = b
⇒ e = 0, f = 0, किन्तु (0, 0) ∈ R × R
इसलिये * के लिये (0, 0) समुच्चय A पर तत्समक अवयव

(3, -5) का प्रतिलोम अवयव
माना (x, y), (3, - 5) का प्रतिलोम अवयव है।
⇒ (3, - 5) * (x, y) = (0, 0)
⇒ (3 + x, - 5 + y) = (0, 0)
संगत अवयव बराबर करने पर
3 + x = 0; - 5 + y = 0
⇒ x = - 3 तथा y = 5
इसलिये (3, - 5) का प्रतिलोम अवयव (-3, 5) है।