RBSE Class 12 Maths Important Questions Chapter 1 Relations and Functions

Rajasthan Board RBSE Class 12 Maths Important Questions Chapter 1 Relations and Functions Important Questions and Answers.

RBSE Class 12 Maths Chapter 1 Important Questions Relations and Functions

Question 1.
Let N be the set of natural numbers and R be relation on N × N defined by (a, b) R (c, d) if ad = be for all a, b,c,d ∈ N. Show that R is an equivalence relation.
Answer:
Given a relation R in N × N, such that (a, b) R (c, d) ⇔ ad = be for all (a, b), (c, d) ∈ N × N.
(i) Reflexive: For (a, b) R (a, b)
⇒ ab = ba, which is true.
So, R is reflexive.

(ii) Symmetric : For (a, b) R (c, d)
⇒ ad = be
⇒ bc = ad
⇒ cb = da
⇒ (c, d) R (a, b) is true.
So, R is symmetric.

(iii) Transitive : For (a, b) R (c, d) and (c, d) R (e,f)
⇒ ad = bc and cf= de .
⇒ \(\frac{a}{b}=\frac{c}{d}\) and \(\frac{c}{d}=\frac{e}{f}\)
⇒ \(\frac{a}{b}=\frac{e}{f}\)
⇒ af = be
So, (a, b) R (e,f) is true.
∴ R is transitive.
Thus, R is reflexive, symmetric and transitive, so R is an equivalence relation.
Hence Proved

Question 2.
Check whether the relation R in the set N of natural numbers given by R = {(a, b): a is divisor of b} is reflexive, symmetric or transitive. Also determine whether R is an equivalence relation. (CBSE 2020)
Answer:
(i) Reflexive: Let n be a natural number.
We know that n divides n, which implies nRn.
So, every natural number is related to itself in relation R.
So, relation R is reflexive.

(ii) Transitive : Let a, b, c be three natural numbers, and let aRb, bRc, aRb implies a divides b and bRc implies b divides c, which combinedly implies that a divides c i.e. aRc.
So, relation R is transitive.

(iii) Symmetric: Let a, b be two natural numbers and let aRb. aRb implies that a divides b but it can't be assured that b necessarily divides a.
Example. 2R4 implies that 2 divides 4 but 4 does not divide 2.
So, relation R is not symmetric.
Since R is reflexive and transitive but not symmetric, thus, R is not an equivalence relation.

Question 3.
Show that the relation R in the set A = {1, 2, 3, 4, 5, 6} given by R = {(a, b): |a - b| is even} is an equivalence relation.
Answer:
Given, A = {1, 2, 3, 4, 5, 6} and R = {(a, b): |a - b| is even}
(i) Reflexive: Let a ∈ A
then |a - b| = 0 is an even number.
∴ (a, a) ∈ R, ∀ a ∈ A
∴ R is reflexive.

(ii) Symmetric : Let a, b ∈ A ∀ (a, b) ∈ R
⇒ |a - b| is even
⇒ |- (b - a)| is even
⇒ |b - a| is even
⇒ |b - a| ∈ R
⇒ (b, a) ∈ R*
∴ R is symmetric.

(iii) Transitive : Let a, b, c ∈ A ∀ (a, b) ∈ R and (b, c) ∈ R
We have |a - b| is even and |b - c| is even
⇒ a-b is even and b-c is even
⇒ (a-b) + (b - c) is even
⇒ (a -c) is even
⇒ | a - c | is even
⇒ (a, c) ∈ R
R is transitive
Thus, R is an equivalence relation. Hence proved.

Question 4.
Check if the realtion R on the set A = {1,2,3,4, 5,6} defined as R = {(x, y): y is divisible by x} is
(i) symmetric
(ii) transitive.
Answer:
Given, A = {1, 2, 3, 4, 5, 6}
R = {(x, y): y is divisible by x]
(i) Reflexive: We know that any number (x) is divisible by itself.
(x, x) ∈ R
R is reflexive.

(ii) Symmetric: Now, (2, 4) ∈ R [as 4 is divisible by 2]
But (4,2) gR [as 2 is not divisible by 4]
R is not symmetric.
(iii) Transitive: Let (x, y), (y, z) ∈ R. Then, y is divisible by x and z is divisible by y.
∴ z is divisible by x.
⇒ (x, y) ∈ R
∴ R is transitive
Thus, R is reflexive and transitive but not symmetric.

Question 5.
Check if the relation R in the set R of real numbers defined as R = {(a, b) :a<b} is (i) symmetric (ii) transitive.
Answer:
Given, R = {(a, b): a < b}
(i) Symmetric:
If (a, b) ∈ R is such that a < b then,
(b, a) ∈ R is not possible.

Example : (2,3) ∈ R, but (3, 2) ∈ R
∴ Relation R is not symmetric.

(ii) Transitive:
If (a, b) ∈ R and (b, c) ∈ R such that a < b and b < c, then clearly, a < c i.e. (a, c) ∈ R
Relation R is transitive.

Question 6.
Show the function f: R → R defined by f(x) = \(\frac{x}{x^2+1}\) as injection, surjection or bijection.
Answer:
We have, a function f:R → R defined by f(x) = \(\frac{x}{x^2+1}\) ∀ x ∈ R
(i) Injection test: Let x₁, x₂ ∈ R such that
⇒ x₁(x₂² + 1) = x₂(x₁² + 1)
⇒ x₁x₂² + x₁ = x₂x₁² + x₂
⇒ x₁x₂(x₂ - x₁) = (x₂ - x₁)
⇒ (x₂ - x₁)(x₁x₂ - 1) = 0
⇒ x₂ = x₁ or x₁x₂ = 1
⇒ x₁ = x₂ or x₁ = \(\frac{1}{x_2}\)
Here, f is not an injection.
∴ f is not one-one.

(ii) Surjection test : Let y ∈ R (condomain) be any arbitrary element.
Consider, y = f(x)
∴ y = \(\frac{x}{x^2+1}\) ⇒ x²y + y = x
⇒ x²y - x + y = 0
⇒ x = \(\frac{1 \pm \sqrt{1-4 y^2}}{2 y}\), which does not exist for 1 - 4y² < 0, i.e. for y > \(\frac{1}{2}\) and y < -\(\frac{1}{2}\)
In particular for y = 1 ∈ R (co-domain), there does not exist any x ∈ R (domain) such that f(x) = y.
∴ f is not surjection.
Thus, f is neither injection nor surjection.

Question 7.
Show that the function f: R - {3} → R - {1} given by f(x) = \(\frac{x-2}{x-3}\) is a bijection.
Answer:
Given, A = R - {3} and B = R - {1}
(i) One-one:
We have, f(x) = \(\frac{x-2}{x-3}\)
Calculate f(x₁):
⇒ f(x₁) = \(\frac{x_1-2}{x_1-3}\)

Calculate f(x₂):
f(x₁) = \(\frac{x_2-2}{x_2-3}\)

Now, f(x₁) = f(x₁)
⇒ \(\frac{x_1-2}{x_1-3}=\frac{x_2-2}{x_2-3}\)
⇒ (x₁ - 2) (x₂ - 3) = (x₂ - 2)(x₁ - 3)
⇒ x₁x₂ - 3x₁ - 2x₂ + 6 = x₁x₂ - 3x₂ - 2x₁ + 6
⇒ -x₁ = - x₂ ⇒ x₁ = x₂
∴ f is an one-one function.

(ii) Onto:
Let y ∈ B = R - {1}
Then, y ≠ 1
Thus, function f is onto if there exists x ∈ A such that f(x) = y.
Now, f(x) = y .
⇒ \(\frac{x-2}{x-3}\) = y ⇒ x - 2 = xy - 3y
⇒ x - 2 = xy - 3y ⇒ x(1 - y) = -3y + 2
⇒ x = \(\frac{2-3 y}{1-y}\) ∈ A [Here y ≠ 1]
So, for any y ∈ B, there exists \(\frac{2-3 y}{1-y}\) ∈ A such that

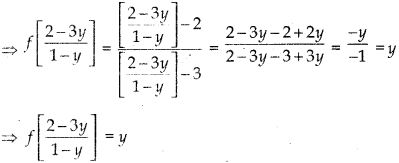
⇒ f is onto.
Since, f is one-one and onto, thus the given function is bijective.

Question 8.
If f: R → R be the function defined by f(x) = 4x³ + 7, then show that f is a bisection.
Answer:
The given function is f:R → R such that f(x) = 4x³ + 7
To show f is bijective, we have to show that/is one-one and into.
(i) One-one function: Let x₁ x₂∈ R such that
f(x₁) = f(x₂).
⇒ 4x₁³ + 7 = 4x₂³ + 7 ⇒ 4x₁³ = 4x₂³ ⇒ x₁³ - x₂³ = 0
⇒ (x₁ - x₂)(x₁² + x₁x₂ + x₂²) = 0
[∵ a³ - b³ = (a - b)(a² + ab + b²)]
⇒ (x₁ - x₂)(x₁² + x₁x₂ + \(\frac{4}{4}\)x₂²) = 0
⇒ (x₁ - x₂)(x₁² + x₁x₂ + \(\frac{1}{4}\)x₂² + \(\frac{3}{4}\)x₂²) = 0
⇒ (x₁ - x₂)[(x₁ + \(\frac{x_2}{2}\))² + \(\frac{3}{4}\)x₂²] = 0
⇒ Either x₁ - x₂ = 0 .............(i)
or (x₁ + \(\frac{x_2}{2}\))² + \(\frac{3}{4}\)x₂² = 0 ..............(ii)
But eq. (ii) gives complex roots as x₁ x₂ ∈ R .
x₁ - x₂ = 0 ⇒ x₁ = x₂
So, f(x₁) = f(x₂) ⇒ x₁ = x₂, ∀ x₁ x₂ ∈ R
Thus, f(x) is a one-one function.

(ii) Onto function : Let y ∈ R (codomain) be any arbitrary number.
Then, f(x) = y ⇒ 4x³ + 7 = y ⇒ 4x³ = y - 7
⇒ x³ = \(\frac{y-7}{4}\) ⇒ x =\( \left(\frac{y-7}{4}\right)^{1 / 3}\)
which is a real number. [∵ y ∈ R]
Thus, for every y ∈ R (codomain), there exists

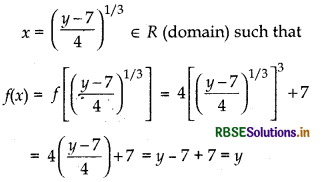
⇒ f(x) is an onto function.
Since, f(x) is both one-one and onto, so it is a bijective.

Question 9.
Given A = {2, 3,4}, B = {2, 5, 6, 7}. Construct an example of each of the following:
(i) An injective map from A to B
(ii) A mapping from A to B which is not injective
(iii) A mapping from A to B.
Answer:
(i) An injective (i.e. one-one) mapping A to B may be defined as f = (2,5), (3, 7), (4, 6)
(ii) A mapping from A to B which is not injective may be defined as g = (2,2), (3, 5), (4, 2). It is many-one.
(iii) A mapping from B to A may be defined as
h = (2,2), (5, 3), (6, 4), (7,4).

Question 10.
Show that the function f: (- ∞, 0) → (-1, 0) defined by f(x) = \(\frac{x}{1+|x|}\), x ∈ (-∞, 0) is one-one and onto
Answer:
Given, f(x) = \(\frac{x}{1+|x|}\)

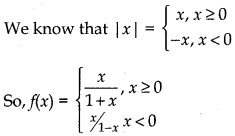
(i) One-one: For x ≥ 0
f(x₁) = \(\frac{x_1}{1+x_1}\) and f(x₂) = \(\frac{x_2}{1+x_2}\)
Putting f(x₁) = f(x₂)
\(\frac{x_1}{1+x_1}=\frac{x_2}{1+x_2}\) ⇒ x₁(1 + x₂) = x₂(1 + x₁)
⇒ x₁ + x₁x₂ = x₂ + x₂x₁ ⇒ x₁ = x₂

For x < 0
f(x₁) = \(\frac{x_1}{1-x_1}\) and f(x₂) = \(\frac{x_2}{1-x_2}\)
Putting f(x₁) = f(x₂)
\(\frac{x_1}{1-x_1}=\frac{x_2}{1-x_2}\) ⇒ x₁(1 - x₂) = x₂(1 - x₁)
⇒ x₁ - x₁x₂ = x₂ - x₂x₁ ⇒ x₁ = x₂
Here, if f(x₁) = f(x₂), then x₁ = x₂
So, f is one-one

(ii) Onto Function : Let y ∈ R (codomain) be any arbitrary element, such that - 1 < y < 1.
When y is positive,
then, f(x) = y ⇒ \(\frac{x}{1+x}\) = y
⇒ x = y + xy ⇒ x(1 - y) = y
⇒ x = \(\frac{y}{1-y}\)

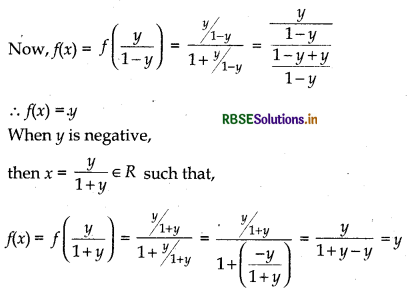
Thus, f is onto.

Question 11.
Show that the function f: N → N defined by f(x) = x² + x + 1 is one-one but not onto. Find the inverse of f: N S, where S is range off.
Answer:
We have, f(x) = x² + x + 1
Now , f(x₁) = x₁² + x₁ + 1
And f(x₂) = x₂² + x₂ + 1
Now, f(x₁) = f(x₂) .
x₁² + x₁ + 1 = x₂² + x₂ + 1
⇒ x₁² - x₂² + x₁ - x₂ = 0
⇒ (x₁ - x₂) (x₁ + x₂) + (x₁ - x₂) = 0,
[Since, a² - b² = (a + b) (a - b)]
(x₁ - x₂) (x₁ + x₂ + 1) = 0
Since, x₁ + x₂ + 1 ≠ 0 for any x ∈ N
x₁ - x₂ = 0 ⇒ x₁ = x₂
So, f is one-one function.

Clearly, f(x) = x² + x + 1 > 3 for all x ∈ N
So, f(x) does not assume values 1 and 2.
∴ f is not an onto function.
Now, if S is the range off, then f: N → S is one-one, onto and hence invertible.
⇒ fof^-1(x) = x, ∀ x ∈ S
⇒ f(f^-1(x)) = x, ∀ x ∈ S
⇒ (f^-1(x))² + (f^-1(x)) + 1 = x, ∀ x e S
⇒ (f^-1(x))² + f^-1 (x) + 1 - x = 0,
which is a quadratic equation in f^-1(x).
∴ f^-1(x) = \(\frac{1 \pm \sqrt{1-4(1-x)}}{2}=\frac{-1 \pm \sqrt{4 x-3}}{2}\)
But f^-1(x) ∈ N
Thus, f^-1(x) = \(\frac{-1+\sqrt{4 x-3}}{2}\)

Question 12.
Let A = R - [2] and B = R - [1] If f:A → B is a function defined by f(x) = \(\frac{x-1}{x-2}\) show that f is one-one and onto. Find f.
Answer:
Given, A = R - {2} and B = R - {1}
f: A → B id defined as f(x) = \(\frac{x-1}{x-2}\)

(i) One-one : Let x, y e A such that f(x) = f(y)
⇒ \(\frac{x-1}{x-2}=\frac{y-1}{y-2}\) ⇒ (x -1) (y - 2) = (x - 2) (y -1)
⇒ xy - 2x - y + 2 = xy - x - 2y + 2
⇒ -2x - y = -x - 2y
⇒ 2x - x = 2y - y
⇒ x = y
So, f is one-one function.

(ii) Onto : Let y ∈ B = R - {1}. Then y ≠ 1.
The function f is onto if there exists x ∈ A such that f(x) = y

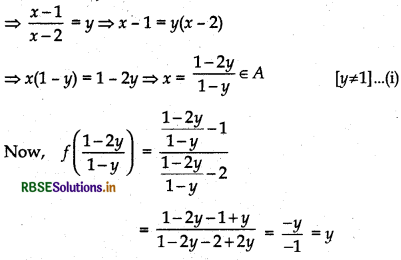
Therefore, f is onto.
Hence, function f is one-one and onto.
From equation (i), we get f^-1(y) = \(\frac{1-2 y}{1-y}\)
⇒ f^-1 (x) = \(\frac{1-2 x}{1-x}\), which is the inverse of f(x)

Question 13.
Let f: R - {\(\frac{4}{3}\)} → R be a function defined as f(x) = \(\frac{4 x}{3 x+4}\). Show that f:R - {\(-\frac{4}{3}\)} → Range (f) is one-one and onto. Hence, find f^-1.
Answer:
It is given that f: R - {-\(\frac{4}{3}\)} → R be a function defined as f(x) = \(\frac{4 x}{3 x+4}\)
Let y be ab arbitrary element of range f.
Then, there exist x ∈ R - {-\(\frac{4}{3}\)} such that y = f(x)

Thus, g is the inverse of f i.e, f^-1 = g
Hence, the inverse of f is the map g: Range f → R - {-\(\frac{4}{3}\)}, which is given by g(y) = \(\frac{4y}{4-3y}\)

Question 14.
Let f: N → N be a function defined as f(x) = 9x² + 6x - 5. Show that f: N → S, where S is the range off, is invertible. Find the inverse of f and hence find f^-1(43) and f^-1(163).
Answer:
We have a mapping f: N → N given by f(x) = 9x² + 6x - 5
(i) One-one function : Let x₁ x₂ e N, such that
f(x₁) = f(x₂)
Then, 9x² + 6xx - 5 = 9x² + 6x2 -5
⇒ 9x₁² + 6x₂ = 9x² + 6x₂
⇒ 9(x₁ -x₂) + 6(x₁ - x₂) =0
⇒ 3(x₁ - x₂) (x₁ + x₂) + 2(x₁ - x₂) = 0 [divide by 3]
⇒ (x₁ - x₂) (3x₁ + 3x₂ + 2) = 0
Either x₁ - x₂ = 0 or 3x₁ + 3x₂ + 2 = 0
But 3x₁ + 3x₂ + 2 ≠ 0 [∵ x₁, x₂ ∈ N]
∴ x₁ - x₂ = 0
⇒ x₁ = x₂
So, f is one-one function.

(ii) Onto function : Obviously, f: N → S is an onto function, because S is the range of f
Thus, f: N → S is one-one and onto function.
⇒ f is invertible function, so its inverse exists.
Let f(x) = y, then y = 9x2 + 6x - 5
⇒ y = (3x)² + 2.3x.1 + 1 - 6 ⇒ y = (3x +1)² - 6
⇒ (3x + 1)² = y + 6 ⇒ 3x + 1 = \(\sqrt{y+6}\)
[taking positive square root as x ∈ N]

Question 15.
Consider a bijective function f: R⁺ → (7, ∞) given by f(x) = 16x² + 24x + 7, where R⁺ is the set of all positive real numbers. Find the inverse function off.
Answer:
The function is given by f(x) = 16x² + 24x + 7
Let y = f(x)
⇒ y = 16x² + 24x + 7
⇒ y = 16x² + 24x + 7 + 2 - 2
⇒ y = 16x² + 24x + 9 - 2
⇒ y = (4x + 3)² - 2
⇒ (4x + 3)² = y + 2
⇒ 4x + 3 = \(\sqrt{y+2}\)
x = \(\frac{\sqrt{(y+2)}-3}{4}\)
Now, y = f(x)
Thus, f^-1 = x = \(\frac{\sqrt{(y+2)}-3}{4}\)

Question 16.
If S is the set of all rational numbers except 1 and * be defined onSbya*b = a + b-ab for all a, b ∈ S. Prove that:
(i) * is a binary operation on S.
(ii) * is commutative as well as associative
Answer:
(i) We know that, addition of two rational numbers is a rational number. Also, multiplication of two rational numbers is also a rationaF number.
Here, a and b are rational numbers other than 1. So, a + b - ab is also a rational number [Since, difference of two rational numbers is a rational number]. So * is a binary operation on set S.

(ii) Commutative:
a* b = a + b-ab-b + a-ba
⇒ a * b = b * a
Hence, * is commutative.
Associative: (a* b)* c = (a + b - ab)* c
= a + b - ab + c - (a + b - ab)c
=a + b + c - ab - bc - ac + abc ...(i)
and a* (b * c) = a* (b + c - bc)
= a +b + c - bc - a (b + c - bc)
= a + b + c - ab - be - ac + abc ...(ii)
From (i) and (ii), we have (a* b)* c = a* (a* c)
Hence, * is associative.

Question 17.
Consider the binary operation * on the set {1, 2, 3, 4, 5} defined by a * b = min (a, b). Write operation table of operation *.
Answer:
Given, binary operation is a * b = min {a, b} defined on the set {1, 2, 3, 4, 5}.
The operation table for Operation * is given as follows.

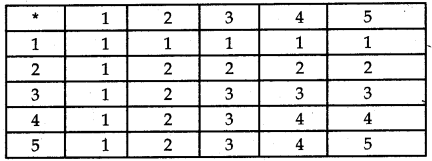
[∵ 1 * 1 = min {1,1} = 1, 1 * 2 = min {1,2} = 1
5*4 = min (5, 4} = 4,
5*4 = min {5, 5} = 5

Question 18.
If the binary operation * on the set of integers Z, is defined by a * b = a + 3b², then find the value of 8 * 3.
Answer:
Given, a * b = a + 3b², ∀ a, b ∈ Z
On putting a = 8,b = 3 then
8 * 3 = 8 + 3. 3² = 8 + 27 = 35

Question 19.
Let * is a binary operation on N given by a * b = LCM (a, b) for all a,b ∈ N. Find 5 * 7.
Answer:
Given a * b = LCM (a, b), ∀ a,b ∈ N
5 * 7 = LCM (5, 7) = 35

Question 20.
Let * is a binary operation on the set of all non¬zero real numbers, given by a* b = ab/5 for all a, b ∈ R - {0}. Find the value of x, given that 2 * (x * 5) = 10.
Answer:
Given, a* b = \(\frac{ab}{5}\), ∀ a, b ∈ R - {0} ...(i)
Also, given, 2* (x* 5) = 10
⇒ 2*\(\left[\frac{x \times 5}{5}\right]\) = 10
⇒ 2* x = 10 ⇒ \(\frac{2x}{5}\) = 10
⇒ x = 25

Multiple Choice Questions

Question 1.
Let R be a reflexive relation of a finite set A having n elements and let there be m ordered pairs in R. Then
(a) m ≥ n
(b) m ≤ n
(c) m = n
(d) None of these
Answer:
(a) m ≥ n

Question 2.
Let R be a relation in N defined by R = {(1 + x, 1 + x²) /x ≤ 5, x ∈ N} which of the following is false?
(a) R = {(2, 2), (3, 5), (4, 10), (5, 17), (6, 25)}
(b) Domain of R = {2,3,4, 5, 6}
(c) Range of R = (2,3,4,5, 6}
(d) (b) and (c) are true
Answer:
(a) R = {(2, 2), (3, 5), (4, 10), (5, 17), (6, 25)}

Question 3.
The relation R on numbers has the following properties:
(i) a < a ∀ a ∈ R (Reflexivity)
(ii) If a < b and b < a then a = b ∀ a,b ∈ R (Antisymmetry)
(iii) If a < b and b < c then a < c ∀ a, b ∈ R (Transitivity) Which of the above properties the relation c on p(A) has?
(a) (i) and (ii)
(b) (i) and (iii)
(c) (ii) and (iii)
(d) (i), (ii) and (iii)
Answer:
(d) (i), (ii) and (iii)

 

Question 4.
A relation R is defined in the set of integers I as follows (x, y) ∈ R if x² + y² = 9 which of the following is false?
(a) R = {(0, 3), (0, -3), (3, 0), (-3, 0)}
(b) Domain of R = {- 3, 0, 3}
(c) Range of R = {- 3, 0, 3}
(d) None of the above
Answer:
(d) None of the above

Question 5.
Let R be the real line consider the following subsets of the plane R × R S = {(x,y)/y = x + 1 and 0 < x < 2},. T = {(x, y)/x - y is an integer} Which one of the following is true?
(a) T is an equivalence relation on R but S is not
(b) Neither S nor T is an equivalence relation on R
(c) Both S and T are equivalence relation on R
(d) S is an equivalence relation on R but T is not
Answer:
(a) T is an equivalence relation on R but S is not

Question 6.
If A is the set of even natural numbers less than 8 and B is the set of prime numbers less than 7, then the number of relations from A to Bis:
(a) 2⁹
(b) 9²
(c) 3²
(d) 2⁹ - 1
Answer:
(a) 2⁹

Question 7.
Let W denotes the words in the English dictionary define by the relation R by R = {(x, y) ∈ W × W the word x and y have at least one letter in common}. Then R is:
(a) Not reflexive, symmetric and transitive
(b) Reflexive, symmetric and not transitive
(c) Reflexive, symmetric and transitive
(d) Reflexive, not symmetric and transitive
Answer:
(b) Reflexive, symmetric and not transitive

Question 8.
Given the relation on R = {(a, b), (b, c)} in the set A = {a, b, c}. Then the minimum numbers of ordered pairs which added to R make it an equivalence relation is:
(a) 5
(b) 6
(c) 7
(d) 8
Answer:
(c) 7

Question 9.
Let R be the relation over the set N × N and is defined by (a, b) R (c, d) ⇒ a + d = b + c. Then R is :
(a) Reflexive only
(b) Symmetric only
(c) Transitive only
(d) An equivalence relation
Answer:
(d) An equivalence relation

Question 10.
Which one of the following relations on R is an equivalence relation?
(a) aR₁b ⇔ |a| = |b|
(b) aR₂b ⇔ a ≥ b
(c) aR₃b ⇔ a divides b
(d) aR₄b ⇔ a < b
Answer:
(a) aR₁b ⇔ |a| = |b|

Question 11.
R = {(x, y) / x, y ∈ I, x² + y² ≤ 4} is a relation in I then domain of R is :
(a) {0,1,2}
(b) {- 2, - 1, 0}
(c) {- 2, -1, 0,1, 2}
(d) {- 2, -1}
Answer:
(c) {- 2, -1, 0,1, 2}

Question 12.
An integer m is said to be related to another integer n if m is a multiple of n then the relation is :
(a) Reflexive and symmetric
(b) Reflexive and transitive
(c) Symmetric and transitive
(d) Equivalence relation
Answer:
(b) Reflexive and transitive

Question 13.
Which of the following defined on Z is not an equivalence relation:
(a) (x, y) ∈ S ⇔ x ≥ y
(b) (x, y) ∈ S ⇔ x = y
(c) (x, y) ∈ S ⇔ x - y is a multiple of 3
(d) (x, y) ∈ S is |x - y| is even
Answer:
(a) (x, y) ∈ S ⇔ x ≥ y

Question 14.
If S is defined on R by (x, y) ∈ S ⇔ xy ≥ 0, then S is
(a) an equivalence relation
(b) reflexive only
(c) symmetric only
(d) transitive only
Answer:
(a) an equivalence relation

Question 15.
If A = {1,2,3}, then the number of equivalence relation containing (1, 2) is :
(a) 1
(b) 2
(c) 3
(d) 8
Answer:
(b) 2

Fill in the Blanks

Question 1.
A relation JR in a set A is called an ____________ relation, if no element of A is related to any element of A.
Answer:
empty

Question 2.
Both the empty relation and the universal relation are sometimes called ____________ relations.
Answer:
trivial

Question 3.
To study ____________ relation, we first consider three types of relations, namely reflexive, symmetric and transitive.
Answer:
equivalence

Question 4.
If f: R → R be given by f(x) = (3 - x³)^1/3, then fof (x) = ____________
Answer:
x

Question 5.
A relation in a set A is called ____________ relation, if each element of A is related to itself.
Answer:
reflexive

True/False

Question 1.
A relation R in a set A is said to be an equivalence relation if R is reflexive and transitive.
Answer:
False

Question 2.
Transitive relation R in X is a relation satisfying (a, b) ∈ R implies that (a, c) ∈ R.
Answer:
True

Question 3.
A function f: X → Y is bijective, if/is both one-one and onto.
Answer:
True

Question 4.
A function f: X → Y is invertible if and only if f is surjective.
Answer:
False

Question 5.
A binary operation * on a set A is a function * from A ∩ A to A.
Answer:
False