RBSE Class 12 Chemistry Important Questions Chapter 3 Electrochemistry

Rajasthan Board RBSE Class 12 Chemistry Important Questions Chapter 3 Electrochemistry Important Questions and Answers.

RBSE Class 12 Chemistry Chapter 3 Important Questions Electrochemistry

Multi Choice Questions (MCQ):

Question 1.
The values of standard E°red of A, B and C are 0.68 V, -2.54 V and -0.50 V respectively. The relative order of their reducing power will be:
(a) A > B > C    
(b) A > C > B
(c) C > B > A    
(d) B > C > A
Answer:
(d) B > C > A

Question 2.
Cell reaction is spontaneous, when
(a) E°red is positive 
(b) ∆G° is negative 
(c) ∆G° is positive
(d) E° red is negative
Answer:
(b) ∆G° is negative 

 

Question 3.    
Which of the following metals does not displace hydrogen by reaction with acids in electrochemical series?
(a) Ba, Sr, Ca    
(b) Cu, Ag, Au
(c) Zn, Fe, Pb    
(d) Na, K, Mg
Answer:
(b) Cu, Ag, Au

Question 4.    
The value of electrode potential of standard hydrogen electrode is:
(a) 0 V    
(b) 1.0 V
(c) 1.10 V    
(d) 0.25 V 
Answer:
(b) 1.0 V

Question 5.    
The metal which oxidised easily, is:
(a) Fe    
(b) Pt
(c) Cu    
(d) Ag
Answer:
(a) Fe    

Question 6.
Which of the following metal can not displace hydrogen from acids on the basis of electrochemical series?
(a) A₁    
(b) Hg
(c) Pb    
(d) Ba
Answer:
(a) A₁ 

Question 7.
The conductivity of aqueous solution of an electrolyte depends on:
(a) charge present on ions.
(b) movement of ions.
(c) number of ions. 
(d) all of the above.
Answer:
(b) movement of ions.

Question 8.    
The unit of specific conductivity is:
(a) ohm^-1 cm^-1 mol^-1 
(b) ohm^-1 cm^-1 g eqv^-1
(c) ohm^-1 cm^-1    
(d) cm^-1
Answer:
(d) cm^-1

Question 9.    
The required charge for depositing one equivalent weight of silver at cathode will be:
(a) 9.65 x 10⁷C    
(b) 9.65 x 10⁴C
(c) 9.65 x 10³C   
(d) 9.65 x 10⁵C
Answer:
(c) 9.65 x 10³C   

Very Short Answer Questions:

Question 1.    
Represent the galvanic cell in which the reaction.
Zn(s) + Cu²⁺ (aq) → Zn²⁺⁽aq) + Cu(s)
Answer:
The galvanic cell for the given reaction is 

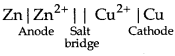
Question 2.    
What is the necessity to use a salt bridge in a Galvanic cell?    
Answer:
The purpose of a salt bridge is not to move electrons from the electrolyte, rather it's to maintain charge balance because the electrons are moving from one-half cell to the other. The electrons flow from the anode to the cathode. 

Question 3.    
Express the relation among the conductivity of a solution in the cell, the cell constant and the resistance of solution in the cell.
Answer:
Conductivity,    
\(k=\frac{1}{\mathrm{R}} \times \frac{l}{\mathrm{~A}}\)
As K = 1/p and p = RA/l
where, k = conductivity, R = resistance and l/A = cell constant

Question 4.    
What is meant by limiting molar conductivity?
Answer:
Limiting molar conductivity The molar conductivity of a solution at infinite dilution is called limiting molar conductivity and is represented by the symbol Am.

Question 5.    
What happens to the cell if an external voltage equal to EMF is applied on it?
Answer:
At this stage, the reaction stops and no current flows through the cell.

Question 6.    
Why is anode negatively charged in an electrochemical cell?
Answer:
Because electrons are released at this electrode.

Question 7.    
What is the difference between EMF and potential difference?
Answer:
EMF is the difference between electrode potential of two half cells when no current is drawn from the Ecell. Potential difference is the difference between electrode potential of two half cells when current is drawn from the cell.

Question 8.    
Is the following reaction feasible or not?
Sn⁴⁺ + 2Fe²⁺ → Sn²⁺ + 2Fe³⁺
Answer:
This reaction is not feasible because reducing power of Sn²⁺ is higher than that of Fe²⁺.

Question 9.    
Which metals cannot displace H₂ from dilute H₂SO₄ solution?
Answer:
The metals which are placed below the hydrogen in electrochemical series i.e., which have +ve reduction potential values cannot displace H₂ from dilute H₂SO₄ solution. For example - Cu, Ag, Au, Pt etc.

Question 10.    
Which metals cannot decompose water vapours? 
Answer:
The metals which are placed below the hydrogen in electrochemical series i.e., which have positive reduction potential values cannot decompose water vapours. Example: Ag, Au, Hg, Cu etc.

Short Answer Questions:

Question 1.    
Define electrochemical cell. What happens when applied external potential becomes greater than E°cell of electrochemical cell? 
Answer:
Electrochemical cell is a device that converts the chemical energy of a spontaneous redox reaction into elec-trical energy.
If the external applied potential becomes greater than E°Cell electrochemical cell, the reaction gets reversed and electrochemical cell now functions as an electrolytic cell.

Question 2.    
Using the E° values of X and Y predict which is better for coating the surface of iron to prevent rust and why?    
Given, 
E°Fe²⁺ /Fe = - 0.44 V
E°x²⁺/x = -2.36 V    
E°y²⁺/Y = -0.14 V
Answer:
Given, E°Fe²⁺ /Fe =  - 0.44 V, 
E°x²⁺/x = - 2.36 V
E°y²⁺/Y  =  -0.14 V
'X' is a better for coating the surface of iron because standard oxidation potential of X is greater than that of Fe so before oxidation of iron takes place, oxidation of X occurs.

Question 3.
The standard electrode potential (E°) for Daniell cell is +1.1 V. Calculate the ∆G° for the reaction 
Zn(s) + Cu²⁺ (aq) —> Zn²⁺ (aq) + Cu(s)
(IF = 96500 C mol^-1).    
Or
The standard electrode potential for Daniel cell is 1.1 V. Calculate the standard Gibbs energy for the cell reaction. (F = 96500 C mol^-1)
Zn(s) + Cu²⁺ (aq) → Zn²⁺ (aq) + Cu(s) 
Answer:
Zn(s) + Cu²⁺ (aq) → Zn²⁺ (aq) + Cu(s)
E° = +1.1 V, 
∆G° = ?
IF = 96500C mol^-1, 
n = 2 ∆G° = -nFE°ell = - 2 x 96500 x 1.1
= - 212300 Jmol^-1

Question 4.    
A zinc rod is dipped in 0.1 M solution of ZnSO₄. The salt is 95% dissociated at this dilution at 298 K. Calculate the electrode potential.
[E°Zn²⁺/Zn = -76V5]    
Answer:
The electrode reaction involved is Zn²⁺ + 2e- → Zn 
Thus, n = 2
By using Nemst equation, we get,
EZn²⁺/Zn =
\(\mathrm{E}_{\mathrm{Zn}^{2+} / \mathrm{Zn}}-\frac{0.0591}{2} \log \frac{1}{\left[\mathrm{Zn}^{2+}\right]}\)
Give that 0.1 M ZnSO₄ solution is 95% dissociated that means.
∴  \(\mathrm{E}_{\mathrm{Zn}^{2+} / \mathrm{Zn}}=-0.76-\frac{0.0591}{2-} \log \frac{1}{0.095}\)
= - 0.76 - 0.0295 [log 1000 - log95] 
= - 0.76 - 0.0295 x 1.022 
[ ∵ log 1000 = 3, log 95 = 1.978]
= -0.79015 V

Question 5.
Given that, the standard electrode potentials (E°) of metals are
K⁺/K = - 2.93 K,    
Ag⁺/Ag = 0.80 V
Cu²⁺/Cu = 0.34 V, 
Mg²⁺/Mg = -2.37 V 
Cr³⁺/Cr = - 0.74 V, 
Fe²⁺/Fe = - 0.44 V 
Arrange these metals in an increasing order of their reducing power.    
Answer:
Reducing power α 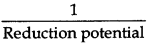 i.e. as the reduction potential decreases, reducing power increases. So arrange the given metals on this basis. Metals in an increasing order of their reducing power. Ag⁺/Ag, Cu²⁺/Cu, Fe²⁺/Fe, Cr³⁺/Cr, Mg²⁺/Mg, K⁺/ K
Ag < Cu < Fe < Cr < Mg < K
(More negative E° means that the redox couple is a stronger reducing agent).

Question 6.    
Calculate ∆,G° and log Kc for the following reaction :
Cd²⁺ (aq) + Zn(s) → Zn²⁺ (aq) + Cd(s)
Given: E°Cd²⁺/Cd = -0.403 v
E°Zn²⁺/Zn = -0.403 V
Answer:
E°Cd²⁺/Cd = - 0.403 V
E°Zn²⁺/Zn = -0.763 V
∴ E°cell = -0.43 - (- 0.763)
E°cell = 0.36V
∵ ∆ G° = -nFE°cell
where n = number of moles of electrons used
n = 2 (Here) => F = 96500 C mol^-1
∴ ∆, G° = - 2 x 96500 x 0.36 = 69480 J/mol
Also E°cell = 0.0591/n log Kc
∴ \(\log \mathrm{K}_c=\frac{n \times \mathrm{E}_{\text {Cell }}^{\circ}}{0.0591}=\frac{2 \times 0.36}{0.0591}\)
log Kc = 12.18

Question 7.    
Consider the following reaction:
Cu(s) + 2Ag⁺ (aq) → 2 Ag(s) + Cu²⁺ (aq)
(i) Depict the galvanic cell in which the given reaction takes place.
(ii) Give the direction of flow of current.
(iii) Write the half-cell reactions taking place at cathode and anode.    
Answer:
(i) Cu/ Cu²⁺ (aq, 1M) | | Ag⁺ (aq, 1M) | Ag 
(ii) Direction of flow of current is from silver to copper.
(iii) At anode Cu (s) → Cu²⁺ (aq) + 2e^-
At cathode 2Ag⁺ (aq) + 2e^- → 2Ag (s)
Net reaction
Cu (s) + 2Ag⁺ (aq) Cu²⁺ (aq) + 2Ag (s)

Question 8.    
Calculate the emf of the following cell at 298 K. 
2Cr(s) + 3Fe²⁺ (0.1M) → 2Cr³⁺(0.01M) + 3Fe(s) Given,
E°(Cr³⁺/Cr) = -0.74 V,
E°(Fe²⁺/Fe) = -0.44 V
Answer:
Since, oxidation of Cr is taking place in the given reac-tion, the chromium electrode is anode and as Fe is reduced in the reaction, Fe electrode is cathode.
The half-cell reactions are as follows
At anode Cr → Cr³⁺ + 3e^-] x 2
At cathode Fe²⁺ + 2e-  → Fe] x 3
Overall reaction
2Cr + 3Fe²⁺ →   2Cr³⁺ + 3Fe
E° = Ecathode - Eanode 
= - 0.44 - (- 0.74) = 0.3 V
\(\mathrm{E}=\mathrm{E}^{\circ}-\frac{0.0591}{n} \log \frac{\left[\mathrm{Cr}^{3+}\right]^2}{\left[\mathrm{Fe}^{2+}\right]^2}\)
Here n = number of electron transferred, i.e equal to 6.
= \(0.3-\frac{0.0591}{6} \log \frac{(0.01)^2}{(0.1)^3}\)
= 0.309 = 0.31 V

Question 9. 
Calculate the emf of the following cell at 25°C. 
Fe | Fe²⁺ (0.001M) || H⁺ (0.01 M) | H₂(g) (1 bar) | Pt (s) 
E°(Fe²⁺/Fe) = -0.44 V; E°(H⁺/H₂) = 0.00V 
Answer:
Write Nernst equation and find the number of electrons to find Ecell. 
At anode, Fe (s) → Fe²⁺ (aq) + 2e ̄ 
At cathode, [H⁺(aq) + e ̄ → 1/2 H₂(g) ] × 2 
Overall reaction 
Fe (s) + 2H⁺ (aq) → Fe²⁺ (aq) + H₂(g) 
Given, 
E°Fe²⁺ /Fe  =  -0.44 V, 
E°H⁺ /H₂  =  0.00V 

Ecell = 0.4104 V 

Question 10. 
Calculate the emf of the following cell at 25°C. 
Zn | Zn²⁺ (0.001M) || H⁺ (0.01 M) | H₂(g) (1 bar) | Pt(s) 
E°(Zn²⁺/Zn) = -0.76 V, 
E°(H⁺/H₂) = 0.00V 
Answer:
At anode Zn(s) → Zn²⁺ (aq) + 2e^- 
At cathode [H⁺(aq) + E^- → 1/2 H₂(g)] x 2
Net equation 
Zn(s) + 2H⁺ (aq) → Zn²⁺ (aq) + H₂ (g) 

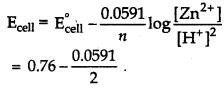
Question 11. 
Calculate the emf of the following cell at 298 K. 
Fe(s) | Fe²⁺ (0.001 M) | | H⁺ (1 M) | H₂(g) (1 bar) | Pt (s) 
[Given, E°cell = +0.44 V] 
Answer:
Write Nernst equation and find the number of electrons to find Ecell. 
Anode half reaction, Fe(s) → Fe²⁺ (aq) + 2e ̄ 
Cathode half reaction, 
[H⁺ (aq) + e^- + H₂(g)] × 2 
Net reaction 
Fe(s) + 2H⁺ (aq) → Fe²⁺ (aq) + H₂(g) 

∴Ecell = 0.44 - [0.02956 × (-3)] 
= 0.44 + 0.08868 
= 0.52868 V ≈ 0.53 V 

Question 12. 
Calculate the emf of the following cell at 25°C. Ag (s) | Ag⁺ (10^-3 M) || Cu²⁺ (10^-1 M) | Cu (s) 
[Given, Ecell = +0.46 V and log 10n = n]
Answer:
Write Nernst equation and find the number of electrons to find Ecell 
As per the condition given, 
Ag(s) Ag⁺ (10^-3 M) | | Cu²⁺ (10^-1 M) | Cu(s) 
At anode Ag(s) → Ag⁺ (aq) + e ̄] × 2 
At cathode Cu²⁺ (aq) + 2e ̄  → Cu(s) 
Overall reaction 
2Ag(s) + Cu²⁺ (as) → 2Ag⁺ + Cu(s) 

Ecell = 0.608 V 

Question 13. 
A strip of nickel metal is placed in a 1 molar solution of Ni(NO₃)₂ and a strip of silver metal is placed in a one molar solution of AgNO₃. An electrochemical cell is created when the two solutions are connected by a salt bridge and the two strips are connected by wires to a voltameter. 
(i) Write the balanced equations for the overall rea tion occurring in the cell and calculate the cell poter tial. 
(ii) Calculate the cell potential, E, at 25°C for the cel if the initial concentration of Ni(NO₃)₂ is 0.100 mol and the initial concentration of AgNO₃ is 1.00 mol 
[E°nI²⁺/nI = - 0.25 v, E°Ag⁺/Ag = 0.80 V, log 10^-1 = -1]
Answer:
(i) Calculate Ecell by using the formula, 
Ecell = Ecathode - Eanode 
(ii) Calculate the number of electrons by writing th electrode reactions then write Nernst equation an find Ecell.
(i) At anode Ni(s) → Ni²⁺ (aq) + 2e^- 
At cathode 2Ag⁺ (aq) + 2e^-  → 2Ag(s) 
Overall reaction 
Ni (s) + 2Ag⁺ (aq) → Ni²⁺ (aq) + 2Ag (s) 
E°cell  = E°cathode - E°anode 
= +0.80 V - (-0.25 V) 
= 1.05 V 
0.0591 

= 1.05 + 0.0295 = 1.0795 V 

Question 14. 
In the button cell, widely used in watches, the following reaction takes place, 
Zn(s) + Ag₂O(s) + H₂O(l) → Zn²⁺ (aq) + 2Ag(s) 2O^-(aq) 
Determine E° and ∆G° for the reaction. 
[Given, E°Ag⁺/Ag = + 0.80V, E°Zn²⁺/Zn = -0.76 V]
Answer:
(i) Calculate E°cell by using the formula, 
E°cell = E°cathode - E°anode 

(ii) Calculate ∆rG° by using the formula, 
∆rG° = -nFE°cell 
The given reaction, shows that zinc is oxidised and silver is reduced in the button cell. 
The reactions occurring are: 
At anode 
Zn(s) → Zn²⁺ (aq) + 2e^- 
E°zn²⁺ /Zn  = - 0.76 V
At cathode 
Ag₂O (s) + H₂O (l) + 2e ̄  → 
2Ag (s) + 2OH ̄ (aq); E°Ag₂₊/Ag  = +0.80 v
Now, E°cell = E°cathode - E°anode 
= 0.80 (-0.76) = 1.56 V 
We know that, 
∆rGo = – nE°F 
Here, n = 2, F = 96500 C mol^-1 
∆rG° = −2 × 1.56 × 96500 C mol^-1 
= -301080 J mol^-1
= -301 kJ mol^-1 

Question 15. 
A voltaic cell is set up at 25°C with the following half-cells. 
Al | Al³⁺ (0.001 M) and Ni | Ni²⁺ (0.50 M) 
Write an equation for the reaction that occurs when the cell generates an electric current and determine the cell potential. 
Answer:
E°Ni²⁺ /Ni = -0.25 V 
and 
E° Al³⁺/Al = - 1.66 V
(log g × 10^-6 = -5.0969) 
Answer:
(i) Calculate E°cell by using the formula. 
E°cell = E°cathode - E°anode 
(ii) Calculate the number of electrons by writing the electrode reactions then write Nernst equation and find E°cell 
For the cells, 
AI | AB³⁺ (0.001 M) || Ni²⁺ (0.50 M) | Ni 
the cell reaction is 
2Al(s) + 3Ni²⁺ (aq) → 2Al³⁺ (aq) + 3Ni (s) 
Thus, n = 6 
E°cell = E°Ni²⁺/Ni  - E°Al³⁺/Al 
= - 0.25 V – (– 1.66 V) = 1.41 V 

= 1.41 V + 0.0502 V = 1.4602 V 

Question 16. 
Determine the values of euqilibrium constant (K) and AG° for the following reaction, 
Ni(s) + 2Ag⁺ (aq) → Ni²⁺ (aq) + 2Ag(s) 
E° = 1.05 V, (1 F = 96500 C mol^-1) 
Answer:
(i) Find ∆G° using the formula, ∆G° = - nFE° 
(ii) Find log K, by using the formula, 
-nFE° = -2.303 RT log Kc 

(iii) Find Kc using the antilog table. 
Here, n = 2 
∆G° = -nFE° 
∆G° = - 2 × 96500 C × 1.05 V 
∆G° = - 202.65 kJ mol^-1 
-nFE° = -2.303 RT log Kc 
[∵ ∆G° = -2.303 RT log Kc] 
\(\log \mathrm{K}_c=\frac{n \mathrm{E}^{\circ}}{0.0591}\)
= \(\frac{2 \times 1,05}{0.0591}\)
Kc = antilog 35.5329 
Kc = 3.412 × 10³⁵ 

Question 17. 
Calculate the potential for half-cell containing 0.10 M K₂Cr₂O₇ (aq), 0.20 M Cr³⁺ (aq) and 1.0 × 10^-4 M H⁺ (aq). 
The half-cell reaction is 
Cr₂O₇^{2 ̄} (aq) + 14H⁺ (aq) + 6e ̄  → 2Cr³⁺ (aq) + 7H₂O (l) 
and the standard electrode potential is given as E° = 1.33 V.
Answer:
Given, [Cr₂O₇^2-] = 0.10 M, 
[Cr³⁺] = 0.20 M and 
[H⁺] = 1 × 10^-4 M, 
E°cell = 1.33 V, n = 6 
Half-cell reaction, 
Cr₂O₇^{2 ̄}(aq) + 14H⁺ (aq) +6e ̄  → 2Cr³⁺ (aq) + 7H₂O(l) 
By using Nernst equation, we get 

= 1.33 V – 0.5477 V = 0.7823 V 

Question 18. 
For the cell, Zn(s) | Zn²⁺ (2 M) || Cu²⁺ (0.5 M) | Cu(s) 
(i) Write the equation for each half reaction. 
(ii) Calculate the cell potential at 25°C. 
[Given, E°zn²⁺/Zn = -0.76 V, 
E°cu²⁺/Cu = +0.34 V] 
Answer:
(i) Calculate E°cell by using the formula, 
E°cell  = E°cathode - E°anode 

(ii) Calculate the number then write Nernst equation and find Ecell. 

(i) The cell reactions are as 

Zn(s) → Zn²⁺(aq) + 2e ̄ 

Cu²⁺(aq) + 2e ̄  → Cu (s) 

(ii) E°cell = E°right - E°left 
E°cell = 0.34 V - (-0.76 V) 
= 1.10 V 

= 1.10 V - 0.0178 V = 1.0822 V 

Question 19. 
Calculate the equilibrium constant, K for the reaction at 298 K. 
Zn(s) + Cu²⁺ (as) Zn²⁺ (aq) + Cu (s) 
AG° = - 212.300 KJ mol^-1
[Given, E°zn²⁺/Zn = -0.76 V, E°Cu²⁺/Cu = +0.34 V] 
Answer:
(i) Find log K, using the formula, 
∆G° = -2.303 log K 
(ii) Find Kc using the antilog table. 
∆G° = -2.303 RT log K 
- 212300 = -2.303 × 8.314 × 298 × log K, 
\(\log \mathrm{K}_c=\frac{212300}{2.303 \times 8.314 \times 298}\)
= 37.2074 
Kc = antilog 37.2074, KC = 1.6 × 10³⁷· 

Question 20. 
Write the Nernst equation and compute the emf of the following cell at 298 K. 
Sn(s) | Sn²⁺ || H⁺ | H₂, 1 atm " Pt (0.05 M) (0.02 M) 
[E Sn²⁺/Sn = -0.144 V] 
Answer:
Cell reaction is 
Sn + 2H⁺ → Sn²⁺ + H₂; (n = 2) 
E°cell - ER - EL = 0 - (-0.144) = 0.144 V 
According to Nernst equation. 

= 0.078 V 

Question 21. 
A copper-silver cell is set up. The copper ion concentration is 0.10 M. The concentration of silver ion is not known. The cell potential when measured was 0.422 V. Determine the concentration of silver ions in the cell. 
[Given, E°Ag⁺/AG = +0.80 v, E°Cu²⁺/Cu = +0.34 V]
Answer:
(i) Write the cell reaction for the given cell. 
(ii) Calculate Ecell by using the formula. 
E°cell = E°right - E°left 
(iii) Calculate Ag+ ion concentration by using Nernst equation. 
Cell reaction is 
Cu(s) + 2Ag⁺ (aq) → Cu²⁺ (aq) + 2Ag (s) 
E°cell = ER - EL 
= +0.80 (+0.34)= 0.46 V 
Number of electrons taking part, n = 2 
By using Nernst equation, 

[Ag_⁺]₂ = 0.00515 
[Ag⁺] = 0.0717 = 7.17 x 10^-2 M 

Question 22. 
One half-cell in a voltaic cell is constructed from a  silver wire dipped in silver nitrate solution of un- known concentration. The other half-cell consists of a zinc electrode in 1.0M solution of Zn(NO₃)₂. A voltage of 1.48 V is measured for this cell.  Use this information to calculate the concentration of silver nitrate solution. 
[Given, E°Zn²⁺/Zn = -0.763 V, E°Ag⁺/Ag  = +0.80 V] 
Answer:
According to given information cell can be represented as 
Zn(s) | Zn²⁺ (aq) (1 M) | | Ag⁺ (aq) | Ag(s) 
Given, E°zn²⁺/Zn = - 0.763 V, E°Ag⁺/Ag = +0.80 V
∴E°cell = E°cathode - E°anode 
= 0.80 (-0.76) = 1.56 V 
By using Nernst equation, we get 

log [Ag⁺] = -1.356 
[Ag⁺] = Antilog [-1.356] 
= 0.0441 = 4.4 × 10^-2 M 

Question 23. 
Calculate the emf of the cell in which the following reaction takes place. 
Ni(s) + 2Ag⁺ (0.002 M) → Ni²⁺ (0.160 M) + 2Ag(s)
[Given that, E°cell = 1.05 V] 
Answer:
E°cell = 1.05 V, 
n = 2 

Ecell = 1.05 - 0.0295 log 4 × 10⁴ 
Ecell = 1.05 -0.0295 × 4.6021 
= 0.91 V 

Question 24. 
A voltaic cell is set-up at 25°C with the following half- cells. 
Ag⁺ (0.001 M) | Ag and Cu²⁺ (0.10 M) | Cu 
What would be the voltage of this cell? 
[Given, E°cell = 0.46 V] 
Answer:
Given E°cell =0.46 V, [Ag⁺] = 0.001 M, [Cu²⁺] = 0.10 M 
Cell reaction is 
Ag⁺ (aq) + Cu(s) → Cu²⁺ (aq) + Ag(s) 
Thus, n = 2 

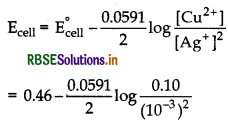
= 0.46 - 0.148 = 0.312 V 

Question 25. 
Explain with a graph, the variation of molar conductivity of a strong electrolyte with dilution. 
Answer:
Strong electrolytes are completely ionised in all con- centrations. For strong electrolytes, A, increases slowly with dilution. It is found to vary with concen- tration according to the Debye-Hucked-Onsager equation. 
\(\Lambda_m=\Lambda_m^{\infty}-\left[\mathrm{A}+\mathrm{B} \Lambda_m^{\infty}\right] \sqrt{\mathrm{C}}\)
where, A and B are called Debye-Hucked constants. If solution is diluted (concentration is decreased), there is decrease in ionic attractions hence, molar conductivity increases with decrease in concentration. 

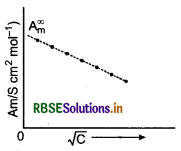
Question 26. 
Calculate the degree of dissociation (a) of acetic acid if its molar conductivity (Am) is 39.05 S cm² mol^-1. Given : λ° (H⁺) = 349.65 cm² mol^-1 
and λ° (CH3COO ̄) = 40.98 cm² mol^-1 
Answer:
To find out the degree of dissociation of acetic acid, 
we first need to calculate the λ°m(CH₃COOH) with  the help of Kohlrausch law, 
According to the question 
Given, λm = 39.05 S cm² mol^-1 
λ° (H⁺) = 349.6S cm² mol^-1 
λ°(CH₃COO ̄) = 40.9 Scm² mol^-1 
λ°m (CH₃COOH) = 2° (H⁺) + 2° (CH₃COO ̄) 
= 349.6 S cm² mol^-1 + 40.9 S cm² mol^-1 = 390.5 S cm² mol^-1 
\(\alpha=\frac{\Lambda_m}{\Lambda_m^{\circ}}=\frac{39.05 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1}}{390.5 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1}}\)
⇒ α = 0.1 

Question 27. 
State Kohlrausch's law of independent migration of ions. Why does the conductivity of a solution decreases with dilution? 
Answer:
Kohlrausch's law of independent migration of ions states that the limiting molar conductivity of an elec- trolyte can be expressed as the sum of the individual contributions of the anion and the cation of the electrolyte, e.g. 
λ°m (CH₃COOH) = λ°CH₃COO^- + λ°H⁺ 
The conductivity of a solution is related with the num- ber of ions present per unit volume of the solution. When the solution is diluted, the number of ions per unit volume decreases. Hence, conductivity or specific conductance of the solution decreases. 

Question 28. 
The conductivity of 0.001 M acetic acid is 4 x 10^-5 S/ cm. Calculate the dissociation constant of acetic acid, if molar conductivity at infinite dilution for acetic acid is 390 S cm²/mol. 
Answer:
(i) First we find out molar conductivity at given concentration using the formula, 
\(\Lambda_{\mathrm{m}}^c=\frac{\kappa \times 1000}{\mathrm{M}}\)

(ii) Then, we find out the degree of dissociation (α) 
using the formula, α = \(\frac{\Lambda_{\mathrm{m}}^{\mathrm{c}}}{\Lambda_{\mathrm{m}}^{\infty}}\)

(iii) After dissociation of acetic acid into ions, we will find out the dissociation constant using the formula, 
\(\kappa_a=\frac{C \alpha^2}{1-\alpha}\)

Question 29. 
Expresses the relation among cell constant resistance of the solution in the cell and conductivity of the solution. How is molar conductivity of a solution related to its conductivity? 
Answer:
The resistance, R of a conductor varies directly with length (2) and inversely with area of cross-section A, i.e. 
R α l/A OR
R = p 1/A 
where, p = resistivity; p = \(\frac{\mathrm{RA}}{l}\)
Conductivity (k) is the reciprocal of resistivity (p). So, 
\(\begin{aligned} &\kappa=\frac{1}{\rho}=\frac{1}{\mathrm{RA} / l}=\frac{l}{\mathrm{RA}}=\frac{1}{\mathrm{R}} \cdot\left(\frac{l}{\mathrm{~A}}\right) \\ &\therefore \kappa=\frac{1}{\mathrm{R}} \cdot\left(\frac{l}{\mathrm{~A}}\right)=\frac{1}{\mathrm{R}} \cdot G^* \end{aligned}\)
where, G* = l/A = Cell constant
The molar conductivity of a solution is related to its conductivity by the following relation 
\(\Lambda_m=\frac{\kappa \times 1000}{\mathrm{M}}\) S cm² mol^-1
where, M = molarity 

Question 30. 
The molar conductivity of a 1.5 M solution of an elec- trolyte is found to be 136.9 S cm² mol^-1. Calculate the conductivity of this solution. 
Answer:
Use formula  λm = imm to find the value of k. 
Given,  λm = 138.9 S cm² mol^-1 
Molarity, M = 1.5 M = 1.5 mol/L 
We know that,  λm  = \(\frac{\kappa \times 1000}{\mathrm{M}}\)
138.9 S cm² mol^-1 = \(\frac{\kappa \times 1000}{1.5 \mathrm{~mol} \mathrm{~cm}^{-3}}\)
\(\kappa=\frac{138.9 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1} \times 1.5 \mathrm{~mol} \mathrm{~cm}^{-1}}{1000}\)
= 138.9 × 1.5 x 10^-3 S cm^-1 
= 0.208 S cm^-1 

Question 31. 
Define conductivity and molar conductivity for the solution of an electrolyte. Discuss their variation with concentration. 
Answer:
Conductivity The inverse of resistivity is called conductivity. It is denoted by k (kappa). It is also known as specific conductance. K = 1/p 
SI unit of conductivity is Sm¹ or ohm^-1 m^-1. Molar conductivity It is defined as the conductance of the solution which contains one mole of the electroelyte such that entire solution is in between the two ha electrodes kept one centimetre apart, and large enough to contain all the electrolytes. 

Molar conductivity,  λm = 1⁄2 Am K/C 
Variation of conductivity and molar conductivity with concentration. 

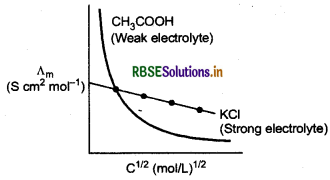
Conductivity and molar conductivity change with change in concentration of electrolyte.  Conductivity always decreases with decrease in concentration for both weak as well as strong electrolytes. But molar conductivity increases with decrease in concentration. For strong electrolytes, Am increases slowly with dilution but for weak electrolyte, A, increases steeply on dilution, especially near lower concentrations. 
Molar conductivity at 0.001 M, 

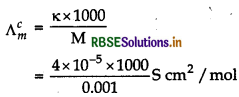
= 40 S cm²/mol 
\(\alpha=\frac{\Lambda_m^c}{\Lambda_m^{\infty}}=\frac{40}{390}\)
For the dissociation of acetic acid, CH₃COOH 
Dissociation constant, Ka = 

= 1.18 × 10^-5 

Question 32. 
Conductivitiy of 2.5 × 10^-4 M methanoic acid is 5.25 x 10^-5 S cm^-1. Calculate its molar conductivity and degree of dissociation. 
Given: λ° (H⁺) = 349.5 S cm² mol^-1 and 2° (HCOO ̄) = 50.5 S cm² mol^-1. 
Answer:
(i) First, we calculate Am using the formula 
\(\Lambda_m^c=\frac{\kappa \times 1000}{\mathrm{M}}\)

(ii) Then, degree of dissociation is calculated using the relation given below. 
\(\alpha=\frac{\Lambda_m^c}{\Lambda_m^{\infty}}\)
Molar conductivity of 2.5 x 10^-4 M solution is
\(\Lambda_m^c=\frac{\kappa \times 1000}{M}=\frac{5.25 \times 10^{-5} \times 1000}{2.5 \times 10^{-4}}\)
λcm = 210 s cm^-2 mol^-1
λm(HCOOH) = λ(HCOO^-) + λ(H⁺)
λm = 50.5 + 349.5
λm = 400
\(\alpha=\frac{\Lambda_m^c}{\Lambda_m^{\infty}}=\frac{210}{400}\)
α = 0.525

Question 33. 
The resistance of 0.01 M NaCl solution at 25°C is 200 n. The cell constant of the conductivity cell used is unity. Calculate the molar conductivity of the solution. 
Answer: 
(i) First find conductivity using the formula conductivity, k = 1/R x l/A

(ii) Then, find molar conductivity of solution by using the formula, 
\(\Lambda_{\mathrm{m}}=\frac{k \times 1000}{\text { Nolarity }}\)
Given Resistance (R) = 200 Ω
Molarity of NaCl solution = 0.01 M
Cell constant = l/A = 1 cm^-1
Conductivity(k) = \(\frac{1}{R} \times \frac{l}{\mathrm{~A}}=\frac{1}{200 \Omega} \times 1 \mathrm{~cm}^{-1}\)
= 5.0 x 10^-3 Ω^-1 cm^-1
Molar conductivity 
\(=\frac{\kappa \times 1000}{\text { Molarity }}=\frac{\left(5.0 \times 10^{-3} \mathrm{~S} \mathrm{~cm}^{-1}\right)\left(1000 \mathrm{~cm}^3 \mathrm{~L}^{-1}\right)}{0.01 \mathrm{~mol} \mathrm{~L}}\)
= 500 S cm² mol^-1 

Question 34. 
The value of λm of Al₂(SO₄)³ is 858 S cm² mol^-1, while λ m(SO₂^-4) is 160 S cm² mol^-1 calculate the limiting ionic conductivity of Al³⁺. 
Answer:
Given, λ°m of Al₂(SO₄)₃ = 858 S cm² mol^-1 
λ°m(SO₂^-4) = 160 S cm² mol^-1 
λ°m [Al₂(SO₄)₃] = 2λ°m(Al³⁺) + 32 λ°m(SO₂^-4) 
858 = 2λ°m(Al³⁺) + 3 × 160 
858 = 2λ°m(Al³⁺) + 480 
\(\lambda_{\mathrm{m}\left(\mathrm{Al}^{3+}\right)}^{\circ}=\frac{858-480}{2}\)
= 189 S cm² mol^-1 

Question 35. 
When a certain conductance cell was filled with 0.1 M KCl, it has a resistance of 85 ohms at 25°C. When the same cell was filled with an aqueous solution of 0.052 M unknown electrolyte, the resistance was 96 ohms. Calculate the molar conductance of the electrolyte at this concentration. 
[Specific conductance of 0.1 M KCl = 1.29 × 10^-2 ohmTM 1 cm^-1] 
Answer:
Given, conductance of cell when electrolyte of 0.1 M 
KCl is filled = 85 ohm's 
Conductance of cell when unknown electrolyte of 0.052 M is filled = 96 ohm's 
Specific conductance (k) of 0.1 M KCl = 1.29 × 10^-2 Ω^-1 cm^-1 
K = 1/R x cell constant 
Cell constant = k × R = 0.0129 S cm^-1 × 85 = 1.0965 cm = 109.65 m^-1
In case of second solution, 
K = 1/R x cell constant 

= 219.61 S cm² mol^-1 

Question 36. 
The electrical resistance of a column of 0.05M NaOH solution of diameter 1 cm and length 50 cm is 5.55 × 10³ Ω. Calculate its resistivity, conductivity and molar conductivity. 
Answer:
(i) Find area from radius by using, А = πr² 
(ii) Find resistivity from the formula, r = RA/l
(iii) Find conductivity (k) from resistivity as к = 1/p 
(iv) Find molar conductivity, λm by using the formula, 
k = 1/p 
\(\Lambda_{\mathrm{m}}=\frac{\kappa \times 1000}{\mathrm{M}}\)
Given, concentration of NaOH = 0.05 M, 
diameter = 1 cm, 
length = 50 cm, 
resistance = 5.55 × 103 N 
Area, 
A = πr²  = 3.14 × 1/2 Cm² 
Resistivity, 
\(=\frac{5.55 \times 10^3 \Omega \times 0.785 \mathrm{~cm}^2}{50 \mathrm{~cm}}\)
= 87.135 Ω cm 

conductivity, K = \(\frac{1}{\rho}=\frac{1}{87.135} \Omega^{-1} \mathrm{~cm}^{-1}\)
= 0.011481.148 x 10^-2 S cm^-1 
Molar conductivity, λm = \(\frac{\kappa \times 1000}{M}\)
= \(\frac{1.148 \times 10^{-2} \times 1000}{0.05}\)
= 229.6 S cm² mol^-1 

Question 37. 
Calculate the degree of dissociation of acetic acid at 298 K, given that 
λm(CH₃COOH) = 11.7 S cm² mol^-1 
λm (CH₃COO ̄) = 40.9 S cm² mol^-1 
λm(H⁺) = 349.1 S cm² mol^-1 
Answer:
Given, λm(CH₃COOH) = 11.7 S cm² mol^-1 
λm(CH₃COO ̄) = 40.9 cm² mol^-1 
λm(H⁺) = 349.1 Scm² mol^-1 
Degree of dissociation, α = \(\frac{\Lambda_{\mathrm{m}}}{\Lambda_{\mathrm{m}}^{\circ}}\)
λm (CH₃COOH) = λm (CH₃COO) + λm (H⁺) 
λm (CH₃COOH) = (40.9 + 349.1) 
= 390 S cm² mol^-1 
α = \(\frac{\Lambda_{\mathrm{m}}}{\Lambda_{\mathrm{m}}^{\circ}}=\frac{11.7}{390}\) = 3.0 x 10^-2
 
Question 38. 
Calculate Am for acetic acid, 
Given that, 
λm (HCl) = 426 S cm² mol^-1
λm (NaCl) = 126 S cm² mol^-1
λm (CH₃COONa) =91 S cm² mol^-1 
Answer:
Recall Kohlrausch's law to find the conductance of weak electrolyte. 
Given, 
λm (HCl) = 426 S cm² mol^-1
λm (NaCl) = 126 S cm² mol^-1
λm (CH₃COONa) =91 S cm² mol^-1 
λm (CH₃COOH) = λH + λCH₃COO^-
= λH⁺ + λCl^- + λCH₃COO^- + λNa⁺ - λCl^- λNa⁺
= λm (HCl) + λm (CH₃COONa) – λm (NaCl) 
= (426 + 91 - 1261) S cm² mol^-1 
= 391 S cm² mol^-1 

Question 39. 
A current of 1.50 A was passed through an electrolytic cell containing AgNO₃, solution with inert electrodes. The weight of silver deposited was 1.50 g. How long did the current flow? (Molar mass of Ag = 10⁸ g mol^-1. 1F = 96500 C mol^-1). 
Answer:
Given, w = 1.50 g; I = 1.50 A 
Molar mass of Ag = 108 mol^-1

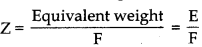
where, F = 96500 C 
As we know, w = Z ×I × t 
or
t = \(\frac{w}{Z \times I}=\frac{1.50 \times 96500}{108 \times 1.50}\)
= 893.51 s 

Question 40. 
The conductivity of a 0.01 M solution of acetic acid at 298 K is 1.65 × 10^-4S cm^-1. Calculate molar conductivity ( λm) of the solution. 
Answer:
Given, conductivity of CH₃COOH solution, 
K = 1.65 × 10^-4 S cm^-1 
Concentration of CH₃COOH solution, 
M = 0.01 M 
Molar conductivity, 
\(\Lambda_{\mathrm{m}}=\frac{\kappa \times 1000}{\mathrm{M}}\)
\(=\frac{\left(1.65 \times 10^{-4}\right) \times 1000}{0.01 \mathrm{M}}\)
= 16.5 S cm² mol^-1 

Question 41. 
Write the name of the cell which is generally used in hearing aids. Write the reactions taking place at the anode and the cathode of this cell. 
Answer:
Mercury cell is suitable for low current devices like hearing aids, watches, etc. 
The electrode reactions of a mercury cell can be written as 
At anode Zn(Hg) + 2OH^- → ZnO(s) + H₂O + 2e 
At cathode HgO(s) + H₂O + 2e ̄  → Hg(l) + 2OH^- 
Overall reaction of the cell is written as 
Zn(Hg) + HgO(s) → ZnO(s) + Hg(l) 

Question 42. 
Write the name of the cell which is generally used in transistors. Write the reactions taking place at the anode and the cathode of this cell. 
Answer:
Leclanche cell is commonly used in transistors. The electrode reaction of Leclanche cell can be written as 
At anode Zn(s) → Zn²⁺ + 2e^- 
At cathode 
MnO₂ + NH⁴⁺ e ^- → MnO(OH) + NH₃ 
NH₃ formed in reaction at cathode combines with Zn²⁺ to form the complex like [Zn(NH₃)₂]²⁺ 

Question 43. 
From the given cells:
Lead storage cell, Mercury cell, Fuel cell and Dry cell Answer the following: 
(i) Which cell is used in hearing aids? 
(ii) Which cell was used in Apollo Space Programme? 
(iii) Which cell is used to automobiles and inverters? 
(iv) Which cell does not have long life? 
Answer:
(i) Mercury cell 
(ii) Fuel cell 
(iii) Dry cell 
(iv) Dry cell 

Question 44. 
Calculate the time to deposit 1.27 g of copper at cathode when a current of 2 A was passed through the solution of CuSO₄. (Molar mass of Cu = 63.5 g mol^-1, 1 F = 96500 C mol^-1) 
Answer:
Given, w = 1.27 g, I = 2A 
Molar mass of Cu = 63.5 g mol^-1 
\(Z=\frac{\text { Equivalent weight }}{F}\)
F = 96500 C mol^-1 
w = Z x I x t 
\(t=\frac{u}{Z \times \mathrm{I}}=\frac{1.27 \times 2 \times 96500}{63.5 \times 2}\)
t = 1930 s
 = 32.1 min 

Question 45. 
(i) Following reactions occur at cathode during the electrolysis of aqueous silver chloride solution: 
Ag⁺ (aq) + e → Ag (s); 
E° = +0.80 V 
H⁺(aq) + e^- → 1/2H₂(g); E° = 0.00 V 
On the basis of their standard reduction electrode potential (E°) values, which reaction is feasible at the cathode and why? 
(ii) Define limiting molar conductivity. Why conductivity of an electrolyte solution decreases with the decrease in concentration? 
Answer:
(i) Electrolysis of an aqueous solution of AgCl. 

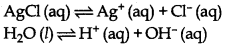
On passing electricity, Ag⁺ (aq) and H⁺ (aq) move towards the cathode. Since, the discharge potential of Ag⁺ ion is lower than that of H⁺ ions. In the other words, Ag⁺ ions have more value of standard reduc- tion potential. Therefore, Ag⁺ ions are discharged in preference of H⁺ ions. 
At cathode 
Ag⁺ (aq) + e ^- →Ag 
Cl + Cl → Cl₂ (g) 
Hence, reduction of Ag⁺ (ion) is feasible at cathode. 

(ii) Limiting molar conductivity Conductivity of an electrolyte solution decreases with the decrease in concentration due to the fact that the number of ions per unit volume that carry the current in a solution decreases on dilution. 

Question 46. 
(i) Following reactions occur at cathode during the electrolysis of aqueous copper (II) chloride solution. Cu²⁺(aq) + 2e → Cu(s), E° = +0.34 V 
H⁺ (aq) + e ̄  → H₂(g); E° = 0.00 V 
On the basis of their standard reduction electrode potential (E°) values, which reaction is feasible at the cathode and why? 
(ii) State Kohlrausch's law of independent migration of ions. Write its one application. 
Answer:
(i) Electrolysis of aqueous solution of CuCl₂ 

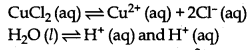
On passing electricity, Cu²⁺ (aq) and H⁺(aq) move towards the cathode. Since, the discharge potential of Cu²⁺ ion is lower than that of H⁺ ions, or Cu²⁺ ion have more value of standard reduction potential. Therefore, Cu²⁺ ions are discharged in the presence of H⁺ ions. 

(ii) Kohlrausch's law of independent migration of  ions 
Application Using this law, it is possible to calculate Am for weak electrolyte from the 2° of individual ions at infinite dilution. 

Question 47. 
Set-up Nernst equation for the standard dry cell. Using this equation show that the voltage of a dry cell decreases with use. 
Answer:
Dry cell (Leclanche cell) consists of a zinc container which acts as anode and cathode is a carbon (graphite) rod surrounded by powdered manganese dioxide and carbon. The space between the electrodes is filled by a moist paste of NH₄Cl and ZnCl₂. 
The reactions are: 
At anode Zn(s) → Zn²⁺ (aq) + 2e ̄ 
At cathode 2e + 2NH⁺ (aq) → 2NH₃ (g) + H₂(g) 
2NH₃(g) + Zn²⁺(aq) → [Zn(NH₃)₂]²⁺ (aq) 
H₂(g) + 2MnO₂  → Mn₂O₃(s) + H₂O(l) 
Overall reaction 
Zn(s) + 2NH⁴⁺ (aq) + 2MnO₂(s) →  [Zn(NH₃)₂]²⁺ (aq) + Mn₂O₃(s) + H₂O(l) 
By using Nernst equation, 
\(\mathrm{E}_{\text {cell }}=\mathrm{E}_{\text {cell }}^{\circ}-\frac{2.303 \mathrm{RT}}{n \mathrm{~F}} \operatorname{In} \frac{\left[\mathrm{Zn}\left(\mathrm{NH}_3\right)_2\right]^{2+}}{\left[\mathrm{NH}_4^{+}\right]}\)
Due to the presence of ions in the overall reaction, its voltage decrease with time. 

Question 48. 
A solution of Ni(NO₃)₂ is electrolysed between plati- num electrodes using a current of 5.0 A for 20 min. What mass of nickel will be deposited at the cathode? 
(Given: Atonic mass of Ni = 58.7 g mol^-1, 1F = 96500 C mol^-1). 
Answer:
(i) First find the amount of charge by Q = 1× t 
(ii) Then, mass of copper deposited using the formula, 
\(m=Z l t=\frac{\text { Equivalent weight }}{96500} \times l \times t\)
Given, Current, I = 5.0 A 
time (t) = 20 × 60 = 1200 s 
Q = I× t ⇒
Q = 5.0 × 1200 = 6000 C 
\(m=\mathrm{Z} \times \mathrm{I} \times t=\frac{\text { Equivalent weight }}{96500} \times \mathrm{Q}\)
= \(\frac{58.7}{2 \times 96500} \times 6000\)
= 1.82 g

Question 49. 
What are fuel cells? Explain the electrode reactions involved in the working of H₂ - O₂ fuel cell. 
Answer:
Those galvanic cells in which chemical energy of com- bustion of fuels like hydrogen, methane, etc. is converted into electrical energy are called fuel cells. The electrode reactions involved in the working of H₂ - O₂ fuel cell are as follows: 
At cathode, 
O₂(g) + 2H₂O(l) + 4e^-  → 4OH^- (aq) 
At anode, 2H₂(g) + 4OH^-(aq) → 4H₂O(l) + 4e^-

Question 50. 
How much electricity in terms of Faradays is required to produce 20 g of calcium from molten CaCl₂? 
Answer:
CaCl₂ → Ca²⁺ + 2Cl^- 

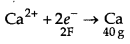
The electricity required to produce 40g = 2F 
Therefore, electricity required to produce 20g 
= (2 × 20) / 40 = 1F 

Question 51. 
Silver is uniformly electrodeposited on a metallic vessel of surface area of 900 cm² by passing a current of 0.5 A for 2 h. 
Calculate the thickness of silver deposited. Given, the density of silver is 10.5 g cm^-3 and atomic mass of Ag = 108 amu. 
Answer:
Electrode reaction, 
\(\mathrm{Ag}^{+}+\underset{1 \mathrm{~F}}{e^{-}} \rightarrow \underset{180 \mathrm{~g}}{\mathrm{Ag}}\)
∴ 96500 C (1F) of electricity deposit Ag
=108g Quantity of current passed Current × Time 
= 0.5 × 60 × 60 × 2 = 3600 C 
3600 C of electricity will deposit Ag 
= \(\frac{108}{96500} \times 3600\)
= 4.03 g 
Now, let the thickness of deposition be a cm 
Mass = volume × Density or Area × Thickness × density 
4.03g = 900 cm² x a cm x 10.5g cm^-3 
a = 4.26 × 10^-4 cm 

Question 52. 
What type of a battery is the lead storage battery? Write the anode and the cathode reactions and the overall reaction occurring in a lead storage battery when current is drawn from it. 
Answer:
Lead storage battery is a secondary cell. Thus, it can be recharged by passing direct current through it. Therefore, it can be reused. It is used in automobiles. In a lead storage cell, the anode is made of spongy lead and the cathode is a grid of lead packed with lead dioxide. The electrolyte used is H₂SO₄ (38% by mass). 
At anode 
Pb(s) + SO₂(aq) → PbSO₄ (s) + 2e ̄ 
At cathode 
PbO₂ (s) + SO₂ (aq) + 4H⁺ (aq) + 2e ̄  → PbSO₄(s) + 2H₂O(l) 
The overall cell reaction 
Pb(s) + PbO₂ (s) + 4H⁺ (aq) + 2SO^{2 ̄} (aq)  → 2PbSO₄(s) + 2H₂O(l) 
On recharging the battery, the reaction is reversed. 
2PbSO₄(s) + 2H₂O(l) → Pb(s) + PbO₂(s) + 4H⁺(aq) + 2SO₂ (aq) 

Question 53. 
The chemistry of corrosion of iron is essentially an electrochemical phenomenon. Explain the reactions occurring during the corrosion of iron in the atmosphere. 
Answer:
The chemistry of corrosion of iron is essentially an electrochemical phenomenon. In which a metal oxide or other salt of metal forms a coating on metal oxide. The reactions occurring during the corrosion of iron in the atmosphere are as follows. 
At anode, 
2Fe(s) → 2Fe⁺ 4e^-; EFe²⁺/Fe = -0.44 V 
At cathode 
O₂(g) + 4H⁺ (aq) + 4e ̄  → 2H₂O(l); 
EH⁺/O₂ H₂O = 1.23 V 
Overall reaction 
2Fe(s) + O₂(g) + 4H⁺(aq) → 2Fe²⁺ (aq) + 2H₂O(l); 
Ecell = 1.67 V 
The ferrous ions are further oxidised to ferric ions by atmospheric oxygen. Reaction is as follows: 
2Fe²⁺ (aq) + 2H₂O(l) + 1⁄4 O₂(g) → Fe₂O₃(s) + 4H⁺(aq) 
 Fe₂O₃ + xH₂O → Fe₂O₃.xH₂O 
Hydrated ferric oxide 

Question 54. 
How many moles of mercury will be produced by electrolysing 10 M Hg(NO₃)₂ plution with a current of 2.00 A for three hours? 
[Hg(NO₃)₂ = 200.6 g mol^-1] 
Answer:
Given, current = 2A, 
Time = 3 h = 3 × 60 × 60 s 
\(m=\mathrm{Zl} t=\frac{\mathrm{E}}{96500} \mathrm{I} t=\frac{200.6 \times 2 \times 3 \times 60 \times 60}{2 \times 9500}\) = 22.4g
Number of moles = \(\frac{22.45}{200.6}\) 
= 0.12 mol 

Question 55. 
In the electrolysis of aqueous sodium bromide, there are two possible anodic reactions. 
2H₂O(l) → O₂(g) + 4H⁺(aq) + 4e^- E° = 1.23 V 
2Br (aq) → Br₂(g) + 2e, E° = 1.08 V 
Which reaction occurs at anode and why? 
Answer:
In the electrolysis of NaBr, 
2Br^-(aq) → Br²⁺ 2e^- 
occurs at anode because it has lower reduction poten- tial, and liberation of O₂ requires over voltage. 

Question 56. 
Mention the reactions occurring at 
(i) anode 
(ii) cathode, during working of a mercury cell. 
Why does the voltage of a mercury cell remain constant during its operation? 
Answer:
Mercury cell 
Anode Zinc-mercury amalgam 
Cathode Paste of HgO and carbon 
Electrolyte Paste of KOH and ZnO 
Electrode reactions are as follows 
At anode 
Zn(amalgam) + 2OH ̄  → ZnO(s) + H₂O + 2e ̄ 
At cathode 
HgO + H₂O + 2e ̄  → Hg(l) + 2OH^- 
Overall reaction 
Zn(amalgam) + HgO(s) → ZnO(s) + Hg(l) 
The voltage of a mercury cell remains constant during its life as the overall reaction does not involve any ion in solution whose concentration can change during its life-time. 

Question 57. 
Give an example of a fuel cell and write the cathode and anode reactions for it. 
Answer:
Fuel cells Galvanic cells that are designed to convert the chemical energy from combustion of fuels like hydrogen, methane, methanol directly into electrical energy are called fuel cells. The efficiency of fuel cell is higher than that of galvanic cell, e.g. hydrogen-oxygen fuel cell, in which hydrogen and oxygen are bubbled through porous carbon electrodes into conc. KOH solution. Finely divided Pt or Pd metals are in- corporated into the electrodes for increasing the rate of electrode reactions. 
At cathode 
O₂(g) + 2H₂O(l) + 4e ̄  → 4OH ̄ (aq) 
At anode 
2H₂(g) + 4OH^-(aq) → 4H₂O(l) + 4e^- 
Overall reaction 
2H₂(g) + O₂(g) → 2H₂O (l) 

Question 58. 
Write the overal reaction that occurs during use (dicharging) of nickel-cademium cell. Is it a primary a secondary cell? Mention its one merit over the lea storage cell. 
Answer:
Nickel-cadmium cell is a secondary cell. It has long life than the lead storage cell but more expensive manufacture. 
The overall reaction during discharging is 

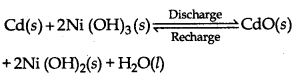
Question 59. 
Chromium metal is electroplated using an acidic s lution containing CrO₃ according to the followin equation: 
CrO₃ (aq) + 6H⁺ + 6e^-  → Cr(s) + 3H₂O 
Calculate how many grams of chromium will be ele troplated by 24,000 coulombs. How long will it take to electroplate 1.5 g chromiu using 12.5 A current? [Atomic mass of Cr = 52 g mol^-1, 1F = 965000 C mol^-1] 
Answer:
Given, Charge (Q) = 24000 C and current (i) = 12.5 A. 
Mass of chromium (Cr) deposited = 1.5 g 
Molar mass of (Cr) = 52 g mol^-1 and 1 F = 96500 Cm 
∵6 × 96500 C charge deposit Cr = 52 g 
∴ 24000 C charge deposit Cr = \(\frac{52 \times 24000}{6 \times 96500}\)
= \(\frac{1248000}{6 \times 96500}\)
Mass of chromium deposited = 2.16 g. 
∵Charge (Q) = i× t (time) 
∴ \(t=\frac{Q}{i}=\frac{24000}{12.5}\)
= 1920 s 
Duration of current = 32 min 

Question 60. 
(i) The cell in which the following reaction occurs 
2Fe³⁺ (aq) + 2I^-(aq) → 2Fe²⁺ (aq) + I₂ (s) 
has Ecell = 0.236 V at 298 K. 
Calculate the standard Gibbs energy of the cell reaction. 
(Given, 1F = 96500 C mol^-1) 
(ii) How many electrons flow through a metallic w if a current of 0.5 A is passed for 2h? 
(given, 1F = 96500 C mol^-1) 
Answer:
(i) Standard Gibbs Free energy is given by 
\(\Delta \mathrm{G}^{\circ}=-n \mathrm{FE}_{\text {cell }}^{\circ}\)
where, n = number of moles of electrons transfered, 
F = Faraday's constant = 96500 Cmol^-1 
Ecell = Cell potential 
Two half-reaction for the given redox reaction can be written as 
2 Fe³⁺ (aq) + 2e ̄  → 2Fe²⁺ (aq) 
2I^-(aq) → I₂(s) + 2e^-
2 moles of electrons are involved in the reaction, hence n = 2 
Therefore, by substituting all the values in Eq. 
(i) we get 
∆G°= -(2 mol) × (96500 C mol^-1) × (0.236 V) = -45548 J 
∆G° = -45.55kJ 

(ii) Given, current (i) = 0.5 A, time (t) = 2h 
Quantity of charge (Q) passed Current (i) × time (t) = (0.5 A) × (2 × 60 × 60 s) = 3600 C 
Again, Q = ne^- 
where, n = number of electrons 
e^- = charge on electron 
∴ \(n=\frac{\mathrm{Q}}{e^{-}}=\frac{3600 \mathrm{C}}{1.6 \times 10^{-19} \mathrm{C}}\) = 2.250 x 10¹⁹
Thus, number of electrons = 2.250 × 10²² 

Question 61. 
(i) Calculate the mass of Ag deposited at cathode when a current of 2A was passed through a solution of AgNO₃ for 15 min. 
(Given: Molar mass of Ag = 10⁸ g mol^-1, 1F = 96500 Cmol^-1). 
(ii) Define fuel cell. 
Answer:
To find out the mass of Ag deposited at cathode, we first need to find the quantity of electricity passed (Q) using faraday's law/The value of Q helps in deter- mining the mass of 10⁸ g of Ag. 
Given, current (l) = LA 
time (t) = 15 min 
Quantity of electricity passed will be 
Q = It = 2x 15 x 60 = 1800 C 
Electrolysis of AgNO₃ 
Ag⁺ + e^- → Ag(s) 
(Atomic mass of Ag = 10⁸ g mol^-1) 
As, 96500 C deposit 10⁸ g of Ag 
∴ 1800 C will deposit = \(\frac{108 \times 1800}{96500}\)
= 2.014 g of Ag 

(ii) A Fuel cell Refer to solution 11. 
The overall reacion of the cell is 
2H₂(g) + O₂(g) → 2H₂O(l) 

Question 62. 
(i) Calculate AG° for the reaction. 
Mg(s) + Cu²⁺ (aq) → Mg²⁺ (aq) + Cu(s) 
(Given, E°cell + 2.71 V, 1F = 96500 C mol^-1) 
(ii) Name the type of cell which was used in Apollo space programme for providing electrical power. 
Answer:
(i) For the reaction, 
Mg(s) + Cu²⁺ (aq) → Mg²⁺ (aq) + Cu(s) n = 2 
E°cell = +2.71 V, 1F = 96500 C mol^-1 (given) 
∆G° = -nF cell 
= -2 × 96500 x 2.71 = -523030 J mol^-1 
= -523.030 kJ mol^-1 
(ii) H₂ - O₂ uel cell was used in Apollo space programme for providing electrical power. 

Question 63. 
(i) Write two advantages of H₂ - O₂ fuel cell over ordinary cell. 
(ii) Equilibrium constant (KC) for the given cell reaction is 10. Calculate E°cell. 

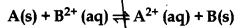
Answer:
(i) Advantages of fuel cells 
(a) Because of the continuous supply of fuels, these cells never become dead. These cells are usually oper- ated at a temperature of 70 - 140°C and gives a poten- tial of about 0.9 V. 
(b) Fuel cells do not cause any pollution unlike ther- mal plant which burn ossil fuels like coal gas, oil, etc. 
(ii) The reaction 
A(s) + B²⁺(aq) ⇒ A²⁺(aq) + B(s) 
By using Nernst equation, 
\(\mathrm{E}_{\text {cell }}=\mathrm{E}_{\text {cell }}^{\circ}-\frac{0.059}{n} \log \frac{\left[\mathrm{A}^{2+}\right]}{\left[\mathrm{B}^{+}\right]}\)
At equilibrium, Ecell = 0 
\(\mathrm{E}_{\text {cell }}^{\circ}=\frac{0.059}{n} \log \mathrm{K}_c\)
Kc = 10 and n = 2
\(\begin{aligned} &\mathrm{E}_{\text {cell }}^{\circ} \doteq \frac{0.059}{2} \log 10 \\ &\mathrm{E}_{\text {cell }}^{\circ}=\frac{0.059}{2}=0.0295 \end{aligned}\)

Question 64. 
An aqueous solution of copper sulphate, CuSO₄ was electrodes using a current of 0.1287 A for 50 min. [Given, atomic mass of Cu = 3.5 g mol^-1] 
(i) Write the cathodic reaction 
(ii) Calculate 
(a) Electric charge passed during electrolysis. 
(b) Mass of copper deposited at the cathode. [Given, 1F = 96500 C mol^-1] 
Answer:
(i) Cathode is the site of reduction. 
(ii) Use Q = It to find the amount of charge passed and 
\(m=\mathrm{Zl} \mathrm{l}=\frac{\text { Equivalent weight } \times \mathrm{I} t}{96500}\)
to find the mass of copper deposited. 
Given that, t = 50 × 60 = 3000 s, I = 0.1287 A 
(i) Cu²⁺ + 2e^- → Cu (s) 
(ii) (a) Q = It = 0.1287 x 3000 = 386.1 C 
Equivalent weight 
= \(\frac{\text { Equivalent weight }}{96500} \times \mathrm{Q}\)

= \(\frac{63.5}{2 \times 96500} \times 386.1\) = 0.127 g

Long Answer Questions:
 
Question 1. 
Calculate the emf and AG for the following cell 
Mg(s) | Mg²⁺ (0.001M) | | Cu²⁺ (0.0001M) | Cu(s) 
E°(Mg²⁺/Mg) = -2.37V, E°(Cu²⁺ /Cu) = 0.34V 
Answer:
At anode Mg(s) → Mg²⁺ (aq) + 2e 
At cathode Cu²⁺ (aq) + 2e^- → Cu(s) 
Overall reaction 
Mg(s) + Cu²⁺ (aq) → Mg²⁺ (aq) + Cu(s) 
E°cell = 0.34 - (-2.37) = + 2.71 V 
(i) ∵ n = 2 
∴ \(E_{\text {cell }}=E_{\text {cell }}^{\circ}-\frac{0.0591}{2} \log \frac{0.001}{0.0001}\)
Ecell 2.71 - 0.0295 log 10 
Ecell = 2.71 - 0.0295 × 1 
Ecell 2.68 ≈ 2.70 V 

(ii) ∆G = nFEcell 
∆G = 2 × 96500 × 2.70 ( 1F96500 C mol^-1) 
∆G = 521.10 kJ mol^-1 

Question 2. 
Calculate the ∆G° and emf (E) that can be obtained from the following cell under the standard condi- tions at 25°C. 
Zn(s) | Zn²⁺ (aq) || Sn²⁺ (aq) | Sn (s) 
[Given, E°(zn²⁺/Zn) = -0.76 V; E°(Sn²⁺/Sn) = -0.14V
and F = 96500 C mol^-1] 
Answer: 
At anode Zn(s) → Zn²⁺ (aq) + 2e^- 
At cathode Sn²⁺ (aq) + 2e^-  → Sn(s) 
Overall reaction 
Zn(s) + Sn²⁺ (aq) → Zn²⁺(aq) + Sn(s) 
E°cell = E°sn²⁺/Sn - (- E°zn²⁺/Zn) 
= - 0.14 + 0.76 = 0.62 V 
∆G° = -nFE° 
= 2 × 96500 × 0.62 
∆G° = -119660 J mol^-1 

Question 3. 
(i) Write the formulation for the galvanic cell in which the reaction Cu(s) + 2Ag⁺(aq) → Cu²⁺ (aq) + 2Ag(s) takes place. Identify the cathode and the anode reactions in it. 
(ii) Write the Nernst equation and calculate the emf of the following cell. 
Sn(s) | Sn²⁺ (0.04 M) | | H⁺(0.02 M) | H₂(g) Pt (s) (1 bar) 
[Given E°(sn²⁺/Sn) = -0.14 V] 
Answer:
(i) Calculate El by using the formula. 
E°cell = E°cathode - E°anode 

(ii) Calculate the number of electrons by writing the electrode reactions, then write Nernst equation and find E°cell.
(i) Refer to solution 9 (iii) 
(ii) At anode Sn(s) → Sn²⁺ (aq) + 2e^-
At cathode 2H⁺ (aq) + 2e → H₂ (g) 
Net reaction 
Sn(s) + 2H⁺ (aq) → Sn²⁺ (aq) + H₂(g) 

= +0.14 V - 0.0591 V = 0.0809 V 

Question 4. 
(i) The conductivity of 0.001 mol L^-1 solution CH₃COOH is 3.905 x 10^-5 S cm^-1. Calculate its mola conductivity and degree of dissociation (a). Give 2° (H⁺) = 349.6 Scm² mol^-1 and 2° (CH₃COO) = 40 Scm² mol^-1. 
(ii) Define electrochemical cell. What happens if external potential applied becomes greater than E of electrochemical cell? 
Answer:
(i) Given: Conductivity of CH₃COOH solution, 
K = 3.905 × 10^-5 S cm^-1 
Concentration of CH₃COOH solution, 
M = 0.001 mol L^-1 = 0.001M 
Molar conductivity, 
\(\begin{aligned} &\lambda_m=\kappa \times \frac{1000}{\mathrm{M}} \\ &=\frac{\left(3.905 \times 10^{-5} \mathrm{~S} \mathrm{~cm}^{-1}\right) \times(1000)}{0.001 \mathrm{M}} \end{aligned}\)
= 39.05 S cm² mol^-1 
Molar conductivity at infinite dilution (λ°m) for CH₃COOH, 
\(=\frac{39.05 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1}}{390.5 \mathrm{Scm}^2 \mathrm{~mol}^{-1}}=0.1\)
= 40.9 + 349.6 S cm² mol^-1 
= 390.5 S cm² mol^-1 
Degree of dissociation, a = \(\frac{\lambda_m}{\lambda_m^{\circ}}\)

(ii) A device used to convert the chemical energy produced in a spontaneous redoxreaction into electrical energy is called an electrochemical cell. When external potential applied becomes greater than E°cell = of electrochemical cell, electrons flow from cathode to anode, i.e. electrochemical cell behaves like an electrolytic cell. 

Question 5. 
(i) Define the term degree of dissociation. Write an expression that relates the molar conductivity of a weak electrolyte to its degree of dissociation. 
(ii) For the cell reaction, Ni(s) | Ni²⁺ (aq) | | Ag⁺ (aq) | Ag(s) 
Calculate the equilibrium constant at 25°C. 
How much maximum work would be obtained by operation of this cell? 
E°Ni²⁺ /Ni = 0.25 V and E°Ag⁺/Ag = 0.80 V 
Answer:
(i) Degree of dissociation The ratio of molar conductivity ( λm) at a specific concentration C to the molar conductivity at infinite dilution, i.e. limiting molar conductivity, A is known as degree dissociation. At any concentration C, if a is the degree of dissociation, then for a weak electrolyte, 
α = \(\frac{\Lambda_m}{\Lambda_m^{\circ}}\)
(ii) Given, E°Ni²⁺ /Ni = 0.25 V and E°Ag⁺/Ag = 0.80 V 
At cathode Sn²⁺(aq) + 2e^- → Sn(s)
Overall reaction
Zn(s) + Sn²⁺(aq) → Zn²⁺(aq) + Sn(s)
E°cell = E°Ag²⁺/Ag - E°Ni²⁺/Ni = 0.80 - 0.25
E°cell = 0.55
Equilibrium constant (K) =
Antilog \(\left(\frac{n \mathrm{E}^{\circ}}{0.0591}\right)\) = \(\operatorname{antilog}\left(2 \times \frac{0.55}{0.0591}\right)\)
K = 4 x 10⁸
Maximumwork (∆G°) = -nFE°
= - 2 x 96500 x 0.55 = 106150 J mol^-1

Question 6. 
(i) Define conductivity and molar conductivity for the solution of an electrolyte. Discuss their variation with concentration. 
(ii) Calculate the standard cell potential of the galvanic cell in which the following reaction takes place : Fe²⁺ (aq) +  Ag⁺(aq) → Fe³⁺ (aq) + Ag (s) Calculate the ∆G° and equilibrium constant of the reaction also.
EAg⁺/Ag = 0.80V; E Fe³⁺/Fe²⁺ = 0.77 V
Answer:
Mg(s) + Cu²⁺(0.001 M) → Mg²⁺(0.01 M) + Cu(s)
Given, E°cell = 2.71 M

 When Ecell < 2.71 V; the reactions are reversed and so, the polarity of the electrodes. Thus, current will flow from Mg to Cu.

(ii) Fe²⁺ (aq) + Ag⁺(aq) → Fe³⁺ (aq) + Ag(s) 
E°cell = E° Ag⁺/Ag − (E°Fe³⁺/Fe²⁺ ) 
= 0.80V - 0.77V = 0.03V 
∆rG°= -nFE = -1 × 96500 × 0.03 
= - 2895 J mol^-1 
Equilibrium constant (K) = antilog \(\left(\frac{n \mathrm{E}^{\circ}}{0.0591}\right)\)
K = 3.21

Question 7. 
(i) Define molar conductivity of a solution and explain how molar conductivity changes with change in concentration of solution for a weak and a strong electrolyte. 
(ii) The resistance of a conductivity cell containing 0.001 M KCl solution at 298 K is 1500 Q. What is the cell constant if the conductivity of 0.001 M KCl solution at 298 K is 0.146 × 10^-3 S cm^-1? 
Answer:
(i) Mg(s) + Cu²⁺(0.001 M) → Mg²⁺(0.01 M) + Cu(s)
Given, E°cell = 2.71 M

When Ecell < 2.71 V; the reactions are reversed and so, the polarity of the electrodes. Thus, current will flow from Mg to Cu.

(ii) Given, conductivity, 
K = 0.146 × 10^-3 S cm^-1 
Resistance, R = 1500 N 
∴ Cell constant, G* = к × R 
= 0.146 × 10^-3 × 1500 = 0.219 cm^-1 

Question 8. 
(i) Write the cell reaction and calculate the emf of the following cell at 298 K. Sn(s) | Sn²⁺ (0.004 M) | | H⁺(0.020 M) | H₂(g) (1 bar) | Pt(s) 
(Given: E°sn²⁺/Sn = -0.14 V)
(ii) Give reasons: 
(a) On the basis of E° values, O₂ gas should be liberated at anode, but it is Cl₂ gas which is liberated in the electrolysis of aqueous NaCl. 
(b) Conductivity of CH₃COOH decreases on dilution. 
Answer:
(i) Sn(s) | Sn²⁺ (0.004 M) || H⁺(0.020 M) | H₂(g) (1 bar) | Pt(s) Cell reaction is 
Sn + 2H⁺(0.020 M) → Sn²⁺(0.004 M) + H₂ (1 bar) 
E°cell = E°H⁺1/2H₂ - E°Sn²⁺/Sn
= 0 - (-0.14 V) = 0 + 0.14 V = 0.14 V 
For calculation of emf, apply Nernst equation; 

(ii) (a) From standard oxidation potential it is clear that oxygen gas should be liberated at anode, but its rate of production is very low. In order to increase that we increase the voltage of external battery. Because of which chloride ions get oxidised easily and Cl₂ and gas is liberated at anode.
 
(b) Conductivity of solution is conductance of ions present in unit volume of solution. On dilution number of CH₃COOH ions per unit volume decreases. Hence conductivity decreases. 

Question 9.
(i) For the reaction
2AgCl(s) + H₂(g) (1 atm) → 2Ag(s) + 2H⁺ (0.1 M) + 2Cl^- (0.1 M),
∆G° = - 43600 J at 25° C
Calculate the emf of the cell. [log 10^-n = -n]
(ii) Define fuel cell and write its two advantages.
Answer:
(i) Gibbs energy of reaction is
∆G° = -nFE°cell ................(i)
Given, ∆G° = - 43600 J, n = 2, E°cell = ?,
F = 96500 C moH
On putting the above values in Eq. (i), we get
- 43600 J = - 2 x 96500 x E°cell
E°cell = \(\left(\frac{43600}{2 \times 96500}\right)\)V = E° = 0 22 V
Now using Nemst equation,

(ii) It is galvanic cell in which chemical energy from combustion of fuels is converted into electrical energy. In this type of galvanic cells, reactants are continuously feed to the electrodes, which react to produce electricity and product thus formed are continuously removed. Fuel cells that are designed to corivert the energy of combustion of fuels like hydrogen, methane, methanol, etc. directly into electrical energy are highly efficient (70%) when compared to efficiency thermal power plants (40%).

Fuel cell using and produces electricity
Their two advantages are:
(a) fuel cells are pollution free.
(b) They never become deal due to continuous supply of fuel.
There have been tremendous progress in the develop-ment of new electrode materials, better catalyst and electrolytes for increasing the efficiency of fuel cells.

Question 10.
E°cell for the given redox reaction is 2.71 V
Mg(s) + Cu²⁺(0.001 M) → Mg²⁺(0.01 M) + Cu(s)
Calculate Ecell for the reaction, write the direction of flow of current when an external opposite potential applied is
(i) less than 2.71 V
(ii) greather than 2.71V
Answer:
Mg(s) + Cu²⁺(0.001 M) → Mg²⁺(0.01 M) + Cu(s)
Given, E°cell = 2.71 M

(i) When Ecell < 2.71 V; the reactions are reversed and so, the polarity of the electrodes. Thus, current will flow from Mg to Cu.

Question 11.
(a) A steady current of 2 amperes was passed through two electrolytic cells X and Y connected in series containing electrolytes FeSO₄ and ZnSO₄ until 2.8 g of Fe deposited at the cathode of cell X. How long did the current flow? Calculate the mass of Zn deposited at the cathode of cell Y.
(Molar mass: Fe = 56 g mol^-1 Zn = 65.3 g mol^-1, 1F = 96500 C mol^-1)
(b) In the plot of molar conductivity (Λm) vs square root of concentration (C₁/2), following curves are obtained for two electrolytes A and B.

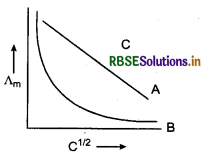
Answer the following
(i) Predict the nature of electrolytes A and B.
(ii) What happens on extrapolation of Λ_m to concentration approaching zero for electrolytes A and B?
Answer:
\(\mathrm{Fe}^{2+}+\underset{2 \mathrm{~F}}{2 e^{-}} \rightarrow \underset{56 \mathrm{~g}}{\mathrm{Fe}}\)
∵ 56 g of Fe is deposited by 2F or 2 x 96500 C charge
∴ 2.8 g of Fe will be deposited by
\(\frac{96500 \times 2 \times 2.8}{56}\)C charge = 9650 C
Now, Q = It
∴ Time, t = \(\frac{9650}{2}\) = 4825 s
Zn²⁺ + 2e^- → Zn
∵ 2 x 96500 C charge deposits Zn = 65.3 g
∴ 9650 C charge will deposit
Zn = \(\frac{65.3 \times 9650}{96500 \times 2}\) = 3.27 g
(b) (i) 'A' is a strong electrolyte since there is a small increase in Λm with increases sharply near high dilution.
(ii) For strong electrolyte (A) the plot becomes linear near high dilution and we can determine the value of Λ°m on extrapolation of Λm to C → 0. For weak electrolyte, Λm increases sharply near high dilution. Hence, an extrapolation of Λm to C → 0 is not possible.

Question 12.
(i) Calculate E°cell for the following reaction at 298 K:
2Al(s) + 3CU²⁺ (0.01 M) → 2Al³⁺ (0.01 M) + 3Cu (s)
Given, Ecell = 1.98 V
(ii) Using the E° values of A and B, predict which is better for coating the surface of iron [E° (Fe²⁺/Fe) = - 0.44 V] to prevent corrosion and why? Given: E° (A²⁺/A) = - 2.37 V, E°(B²⁺/B) = - 0.14 V
Answer:
(i) 2Al(s) + 3Cu²⁺ (0.01 M) → 2Al³⁺ (0.01 M) + 3Cu(s)
Ecell = 1.98 V
Applying Nemst equation for the given cell reaction,
\(\begin{aligned} &\mathrm{E}_{\text {cell }}=\mathrm{E}_{\text {cell }}^{\circ}-\frac{0.0591}{n} \log \frac{\left[\mathrm{Al}^{3+}\right]^2}{\left[\mathrm{Cu}^{2+}\right]^3} \\ &\mathrm{E}_{\text {cell }}^{\circ}=\mathrm{E}_{\text {cell }}-\frac{0.0591}{n} \log \frac{\left[\mathrm{Al}^{3+}\right]^2}{\left[\mathrm{Cu}^{2+}\right]^3} \end{aligned}\)
Here, n = 6 (n - number of electron transfered)
= \(1.98+\frac{0.0591}{6} \log \frac{(0.01)^2}{(0.01)^3}\)
= \(1.98+\frac{0.0591}{6} \log 100\)
[log 100 = log 10² = 2 log 10 = 2, as log 10 = 1]
= 1.9997 V = 2.0 V

(ii) Lower the reduction potential, more reactive is the metal. Coating the surface of iron with a more active metal prevents the iron from losing electrons and hence from corrosion. As reduction potential of A is Lower than that of iron, therefore A would be used for coating the surface of iron to prevent it from corrosion. This is because lower the reduction potential of an element, more reactive is the element. Therefore, A would be more reactive than iron as well as B and hence, A protects the iron metal from corrosion.

Question 13.
(i) Define the following terms:
(a) Molar conductivity (Λm)
(b) Secondary batteries
(ii) State the following laws
(a) Faraday's first law of electrolysis
(b) Kohlrausch's law of independent migration of ions.
Answer:
(i) (a) Molar conductivity, Λm of a solution at a dilution V is defined as the conductance of all the ions produced from one gram mole of the electrolyte dissolved in Vcm³ of the solution when the electrodes are one centimeter apart and the area of the electrodes is so large that the whole of the solution is contained between them.
Λm = k x V or Λm =  \(\frac{\mathrm{k} \times 1000}{\text { Molarity }}\)
Molarity where k is the conductivity and V is the volume of the solution containing 1 mole of the electrolyte.

(b) Secondary batteries After use, they can be re-charged by passing current through it in the opposite direction so that it can be used again. Secondary cell undergo a large number of discharging and charging cycles. The most important secondary cell is the lead storage battery. Other example includes nickel-cadmium cell.

(ii) (a) Faraday's first law of electrolysis The amont of substance deposited during electrolysis is directly proportional to quantity of electricity passed. m ∝ Q, m ∝ It, m = ZIt,
where, Z is electrochemical equivalent, I is current in ampere, t is time in seconds and Q is charge in coulomb.
Electrochemical equivalent (Z) It is amount of substance deposited in grams when I ampere current is passed for 1 second, i.e. when 1 coulomb of charge 5 of passed. Its unit is g C^-1.

(b) Kohlrausch's law of independent migration of ions Kohlrausch's law of independent migration of ions states that equivalent conductivity of an electrolyte is equal to the sum of conductance of anions and cations at infinite dilution.

Question 14.
(i) Predict the products of electrolysis in each of the following:
(a) An aqueous solution of AgNO₃ with platinum electrodes.
(b) An aqueous solution of H₂SO₄ with platinum electrodes.
(ii) Estimate the minimum potential difference needed to reduce Al₂O₃ at 500°C. The Gibbs energy change for the decomposition reaction.
\(\frac{2}{3}Al2O3 → \frac{4}{3}\)Al + O₂ is -960 kJ. (F = 96500 C mol^-1)
Answer:
(i) (a) Electrolysis of AgNO₃(aq) using Pt electrodes
AgNO₃(aq) → Ag⁺(aq) + NO^-₃(aq)
At cathode, Ag⁺ (aq) + e^- → Ag(s)
At anode, 2H₂O(l) → O₂(g) + 4H⁺ (aq) + 4e^-

(b) Electrolysis of H₂SO₄(aq) using Pt electrodes.
2H₂O(l) → 2H₂(g) + O₂(g)
At cathode, H₂O + e^- → \(\frac{1}{2}\)H₂ + OH^-
At anode, 2H₂O + e^- → O₂ + 4H⁺ + 4e^-

(ii) Reaction involved, \(\frac{2}{3}\)Al₂O₃ →  4/3Al + O₂
Here, n = 4
Given, ∆G = - 960 kJ ⇒ ∆G = nFE°
-960000 J = -4 x 96500 x E°
E° =  = 2.48 V ≈ 2.5 V

Question 15.
(i) Define the following terms:
(a) Limiting molar conductivity
(b) Fuel cell
(ii) Resistance of a conductivity cell filled with 0.1 mol L^-1 KCl solution is 100 Ω. If the resistance of the same cell when filled with 0.02 mol L^-1 KCl solution is 520 Ω, calculate the conductivity and molar conductivity of 0.02 mol L^-1 KCl solution. The conductivity of 0.1 mol L^-1 KCl solution is 1.29 x 10^-2 Ω^-1 cm^-1.
Answer:
(i) (a) Limiting molar conductivity The molar conductivity of a solution at infinite dilution is called limiting molar conductivity and is represented by the symbol Λ°m.

(b) Fuel cell Fuel cells require a continuous input of fuel and an oxidizing agent (generally oxygen) in order to sustain the reactions that generate the electricity. Therefore, these cells can constantly generate electricity until the supply of fuel and oxygen is cut off. Despite being invented in the year 1838, fuel cells began commercial use only a century later when they were used by NASA to power space capsules and satellites. Today, these devices are used as the primary or secondary source of power for many facilities including industries, commercial buildings, and residential buildings. A fuel cell is similar to electrochemical cells, which consists of a cathode, an anode, and an electrolyte. In these cells, the electrolyte enables the movement of the protons.

(ii) (a) First calculate the cell constant using relation.
l/A (cell constant) = R x k then, find

(b) Find molar conductivity of solution by the formula,
Λm = \(\frac{\kappa \times 1000}{\text { Molarity }}\)
(a) Cell constant,
G° = conductivity x resistance
= 1.29 S m^-1 x 100Ω = 129 m^-1 = 1.29 cm^-1
(b) Conductivity of 0.02 M KCl solution,
k = \(\frac{\text { Cell constant }}{\text { Resistance }}=\frac{1.29 \mathrm{~cm}^{-1}}{520 \Omega}\)
= 2.48 x 10^-1 S cm^-1
(c) Molar conductivity, Λm = \(\frac{\kappa \times 1000}{M}\)
= \(\frac{2.48 \times 10^{-3} \times 1000}{0.02}\) = 124 S cm² mol^-1

Question 16.
(i) State Faraday's first low of electrolysis. How much charge in terms of Faraday's is required for the reduction of 1 mole of Cu²⁺ to Cu.
(ii) Calculate emf of the following cell at 298 K.
Mg(s) | Mg²⁺(0.1M) | | Cu²⁺ (0.01) | Cu(s)
Given, E°cell = +2.71 V,
1F = 96500 C mol^-1
Answer:
(i) Faraday's first law of electrolysis: The amount of chemical reaction and hence the mass of any substance deposited or liberated at any electrode is directly proportional to the quantity of electricity passed through the electrolyte (solution or melt).
Cu²⁺ + 2e^- → Cu
So, two Faraday of charge is required
Charge required for the reduction of 1 mole of Cu₂+ to Cu = 2F

(ii) Cu²⁺ + Mg → Mg²⁺ + Cu
Given, E°cell =+2.71 V
By using Nemst equation,
Ecell = E°cell - \(\frac{0.059}{n} \log \frac{\left[\mathrm{Mg}^{2+}\right]}{\left[\mathrm{Cu}^{2+}\right]}\)
Here, n = 2 and E°cell = + 2.71 V
∴ Ecell = 2.71 - \(\frac{0.059}{2} \log \frac{(0.1)}{(0.01)}\)
= 2.71 - \(\frac{0.059}{2}\)log 10
= 2.71 - 0.0295 = 2.68 V [∵ log 10 = 1]

COMPETITION CORNER: 

Question 1.
The number of electrons deposited at cathode during electrolysis by 1 A current in 60 s (Charge of electron = 1.60 x 10^-19 C):
(a) 7.48 x 10²³
(b) 6 x 10²³
(c) 6 x 10²⁰
(d) 3.75 x 10²⁰
Answer:
(d) 3.75 x 10²⁰

Question 2.
How much time is required for the formation of 0.10 mol chlorine gas from 3A current during the electrolysis of molten sodium chloride?
(a) 330 min
(b) 55 min
(c) 110 min
(d) 220 min
Answer:
(c) 110 min

Question 3.
Which aqueous solution of following compounds is best conductor of electric current?
(a) acetic acid
(b) hydrochloric acid
(c) ammonia
(d) fructose
Answer:
(b) hydrochloric acid

Question 4.
The ratio of equivalent conductivity and specific conductivity of 0.01 N NaCl solution at a certain temperature is:
(a) 10⁵ cm³
(b) 10³ cm3
(c) 10 cm³
(d) 10_⁸ cm³
Answer:
(a) 10⁵ cm³

 

Question 5.
How much weight of copper will be deposited by passing 2 F electric charge from cupric salt solution? (Atomic weight of Cu = 63.5)
(a) 2.0 g
(b) 3.175 g
(c) 63.5 g
(d) 127.0 g
Answer:
(c) 63.5 g

Question 6.
Some half-cell reactions are given below:
Mn₂ + 2e^- → Mn; E° = -1.18 V
2 (Mn²⁺ + e^- → Mn); E° = +1.51 V
E° for 3 Mn²⁺ → Mn + 2Mn³⁺ will be:
(a) - 2.69 V; reaction will not occur
(b) -2.69 V; reaction will occur
(c) -0.33 V; reaction will not occur
(d) -0.33 V; reaction will occur
Answer:
(a) - 2.69 V; reaction will not occur

Question 7.
Button cell in watches acts as following method
Zn(s) + Ag₂O(s) + H₂O(l)  ⇌ 2Ag(s) + Zn(aq) + 2OH^-(aq)
If half cell potential is:
Zn²⁺(aq) + 2e^- → Zn(s); E° = - 0.76 V
Ag₂O(s) + H₂O(l) + 2e^- → 2Ag(S) + 2OH^-(aq); E° = 0.34 V
then cell potential will be:
(a) 1.34 V
(b) 1.10 V
(c) 0.42 V
(d) 0.84 V
Answer:
(b) 1.10 V

Question 8.    
A hydrogen gas electrode is formed by dipping it in 10 pH solution of hydrochloric acid and by passing hydrogen gas at 1 atm. Which of the following is its oxidation potential?
(a) 1.81V
(b)0.059 V
(c) 0.59 V
(d) 0.118 V
Answer:
(c) 0.59 V

Question 9.
The equivalent conductivity of potassium oxalate at infinite dilution will be (Given: the molar conductivities of oxalate in K⁺ and Na⁺ ions at infinite dilution are 148.2,50.1,73.5 cm² mol^-1 respectively):
(a) 271.8 S cm² eq^-1
(b) 67.95 S cm² eq^-1
(c) 543.6 S cm² eq^-1
(d) 135.9 S cm² eq^-1
Answer:
(d) 135.9 S cm² eq-1

Question 10.
The molar conductivity of 0.1 molar ammonium hy-droxide at 25°C is 9.54 ohm^-1 cm² mol^-1 and its molar conductivity at infinite dilution is 238 ohm^-1 cm₂ mol^-1. The degree of ionization of ammonium hydroxide at that concentration and temperature is:
(a) 40.800%
(b) 2.080%
(c) 20.800%
(d) 4.008%
Answer:
(d) 4.008%

Question 11.
The values of of following reactions are given below:
Fe³⁺(aq) + e- → Fe²⁺(aq); E°= 0.771 V
Fe²⁺(aq) + 2e- → Fe(s); E° = 0.447 V
What will be the charge in free energy for the reaction Fe³⁺(aq) + 3e^- → Fe(s)?
(a) +18.51 kJ mol^-1
(b) +11.87 kJ mol^-1
(c) -8.10 kJ mol^-1
(d) -10.41 kJ mol^-1
Answer:
(b) +11.87 kJ mol^-1

Question 12.
Four consecutive members of first series of transition metals are given below. For which member, the value of standard potential (E° M²⁺/M) is of positive sign?
(a) CO (Z = 27)
(b) Ni (Z = 28)
(c) Cu (Z = 29)
(d) Fe (Z = 26)
Answer:
(c) Cu (Z = 29)