RBSE Class 12 Chemistry Important Questions Chapter 1 The Solid State

Rajasthan Board RBSE Class 12 Chemistry Important Questions Chapter 1 The Solid State Important Questions and Answers.

RBSE Class 12 Chemistry Chapter 1 Important Questions The Solid State

Multiple Choice Questions (MCQ):

Question 1. 
The value of coordination number in hexagonal close packing (hcp) is:
(a) 12 
(b) 8
(c) 6
(d) 4
Answer:
(a) 12 

Question 2. 
What will be the edge length of unit cell of a face-centred cubic lattice if radius of sphere present in it is 500 pm?
(a) 1414 pm
(c) 500 pm
(b) 1000 pm
(d) 250 pm
Answer:
(a) 1414 pm

 

Question 3. 
Solid AB has NaCl type of structure, if radius is 100 pm then radius of B will be:
(a) 241 pm
(b) 100 pm
(c) 50 pm
(d) 200 pm
Answer:
(a) 241 pm

Question 4. 
The example of 8 : 8 coordination is:
(a) CsCl
(b) ZnS
(c) Ka
(d) CaF₂
Answer:
(a) CsCl

Question 5. 
The number of octahedral voids for each sphere in face centred cubic structure will be:
(a) 8
(c) 2
(b) 4
(d) 1
Answer:
(d) 1

Question 6. 
A metal is crystallised in face-centred cubic arrange- ment. If edge length of unit cell iso and radius of metal atom is r, then:

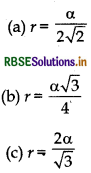
(d) None of these
Answer:
\(\text { (a) } r=\frac{\alpha}{2 \sqrt{2}}\)

Question 7. 
The density of cubic unit cell can be given by following formula: 

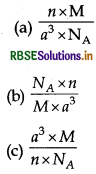
(d) None of these
Answer:
\(\text { (a) } \frac{n \times \mathrm{M}}{a^3 \times \mathrm{N}_{\mathrm{A}}}\)

Question 8. 
In a solid lattice structure, atoms W are present at corners of cube, atoms O at centre of edges and atoms Na at centre of cube. The formula of solid will be: 
(a) NaWO₂
(b) Na₂WO₃ 
(c) NaWO₃
(d) NaWO₄ 
Answer:
(c) NaWO₃

Question 9. 
A substane is crystallized in face-centred cubic structure. Atom A is present at each corner and atom Bat centre of each face. The correct composition of A_xB_y will be. 
(a) AB₃
(b) A₄B₃ 
(c) A₃B
(d) None of these 
Answer:
(a) AB₃

Question 10. 
If parameters of unit cell of crystal system of a compound is as follow: -0.387, b=0.387,c=0.505 nm and a = B = 90°, y = 120°. What will be the crystal system? 
(a) Cubic
(b) Hexagonal 
(c) Orthrhombic 
(d) Rhombohedral 
Answer:
(b) Hexagonal 

Question 11. 
The total volume of atoms present in face-centred cubic unit cell is:

Answer:
\(\text { (c) } \frac{16}{3} \pi r^3\)

Question 12. 
If CsBr is crystallized in bec lattice and edge length of unit cell is 436.6 pm. If atomic masses of Cs and Br are 133 g/mol and 80 g/mol and Avogadro number is 6.022 x 10² then density of CsBr will be: 
(a) 0.425 g cm^-3 
(b) 8.25 g cm^-3
(c) 4.25 g cm^-3 
(d) 42.5 g cm^-3
Answer:
(c) 4.25 g cm^-3 

Very Short Answer Questions:

Question 1. 
Which point defect in crystals not alter the density of the relevant solid? 
Answer:
Frenkel defect.

Question 2. 
Which point defect in its crystal units alters the density of a solid? 
Answer:
Schottky defect.

Question 3. 
Which point defect in its crystal units increases the density of a solid? 
Answer: 
Metal excess defect increases the density of a solid. It is due to presence of extra cations in the interstitial sites.

Question 4. 
How do metallic and ionic substances differ in conducting electricity? 
Answer:
The electrical conductivity in metallic substances is due to free electrons while in ionic substances the conductivity is due to presence of ions.

 
Question 5. 
Which point defect of its crystals decreases the density of a solid? 
Answer:
Schottky defect.

Question  6. 
What is the number of atoms in a unit cell of a facecentred cubic crystal? 
Answer: 
The number of atoms in a unit cell of fcc-crystal is 4 atoms.

Question 7. 
Write a feature which will distinguish metallic solid from an ionic solid. 
Answer: 
The electrical conductivity in metallic solid is due to free electrons while in ionic solid the conductivity is due to presence of ions.

Question 8. 
Which point defect in crystals of a solid does not change the density of the solid? 
Answer: 
Frenkel defect.

Question 9. 
Which point defect in crystals of a solid decreases the density of the solid? 
Answer: 
Schottly defect.

Question 10. 
What type of interactions hold the molecules together in a polar molecular solid? 
Answer: 
Dipole-dipole forces of attractions hold the molecules together in a polar molecular solid.

Question 11. 
What type of semiconductor is obtained when silicon is doped with arsenic?
Answer: 
n-type semiconductor.

Question 12. 
Write a distinguishing feature of metallic solids.
Answer: 
Metallic solids possess high electrical and thermal conductivity due to presence of free electrons.

Question 13. 
Crystalline solids are anisotropic in nature. What does this statement mean?
Answer: 
It means that crystalline solids show different values of their some properties like electrical conductivity, refractive index, thermal expansion etc. in different directions. 

Question 14. 
Which stoichiometric defect in crystals increases the density of a solid?
Answer: 
Interstitial defect in crystals increases the density of a solid.

Question 15. 
What is meant by 'doping'in a semiconductor?
Answer: 
Addition of a suitable impurity to a semiconductor to increases its conductivity is called doping. 

Question 16. 
Write a point of distinction between a metallic solid and an ionic solid other than metallic lustre.
Answer:
Metallic solid conducts electricity in solid state but ionic solids do so only in molten state or in solution or metals conduct electricity through electrons and ionic substances through ions. Metallic solids are malleable and ductile while ionic solids are hard and brittle. 

Question 17. 
How may the conductivity of an intrinsic semiconductor be increased?
Answer: 
The conductivity is increased by adding an appropriate amount of suitable impurtiy. This process is called as intrinsic doping. 

Question 18. 
Which stoichiometric defect increases the density of a solid?
Answer:
Interstitial defect increases the density of a solid.

Question 19. 
What are n-type semiconductors?
Answer: 
n-type semiconductor: They are obtained by doping silicon with an element of group 15, like P, As etc. 

Question 20. 
What type of stoichmetric defect is shown by AgBr and Agl?
Answer: 
AgBr shows both Frenkel defect and Schottky defect whereas Agl shows Frenkel defect. 

Question 21. 
What type of defect can arise when a solid is heated?
Answer: 
Vancancy defects can arise when a solid is heated. 

Question 22. 
Why does LiCl acquire pink colour when heated in Li vapours?
Answer: 
This is due to metal excess defect due to anionic vacancies in which the anionic sites are occupied by unpaired electrons (F-centres). 

Question 23. 
How many atoms constitute one unit cell of a face centred cubic crystal?
Answer: 
4 atoms constitute one unit cell of a foc crystal. 

Question 24. 
What type of stoichiometric defect is shown by AgCl?
Answer: 
Frenkel defect is shown by AgCl. 

Question 25. 
What type of substances would make better Permanent Magnets : Ferromagnetic or Ferrimagnetic?
Answer: 
Ferromagnetic substances would make better permanent magnets
Example: Fe, Co, Ni etc. 

Question 26. 
Calculate the number of atoms in a face centred cubic unit cell.
Answer: 
In face centred cubic arrangement, number of lattice points are: 8 + 6.
Lattice points per unit cell = 8 + 6 x 5 = 4 

Question 27. 
On heating a crystal of Clin potassium vapour, the crystal starts exhibiting a violet colour. What is this due to?
Answer: 
The Clions diffuse to the surface and combine with atoms which get ionized by losing electrons. These electrons are trapped in anions vacancies and act as F-centre which imparts violet colour to the crystal. 

Question 28. 
Which type of ionic substances show Schottky defect in solids?
Answer: 
Highly ionic compounds with high coordination number and small difference in size of cations and anions show schottky defect. 

Question 29. 
How many atoms per unit cell (z) are present in bcc unit cell?
Answer: 
Number of atoms in a unit cell of a body centred cubic structure: Contribution by 8 atoms on the corners
= 1/8 x 8 = 1
Contribution by the atom presents within the body = 1  
Total number of atoms present in the unit cell = 1 + 1 = 2 atoms 

Question 30. 
What type of stoichiometric defect is shown by NaCl?
Answer: 
Schottky defect is shown by Nacl. 

Question 31. 
Write a distinguishing feature between a metallic solid and an ionic solid.
Answer: 
The electrical conductivity in metallic substances is due to free electrons while in ionic substances the conductivity is due to presence of ions. 

Question 32. 
Why are crystalline solids anisotropic? 
Answer: 
Crystalline solids show different values of their some properties like electrical conductivity, refractive index, thermal expansion etc. in different direction.

Question 33. 
What is meant by "antiferromagnetism"?
Answer: 
Antiferromagnetism: These substances possess zero nét magnetic moment because of presence of equal number of electrons with opposite spins.

Question 34. 
Write a distinguishing feature of a metallic solid com- pared to an ionic solid.
Answer:
Metallic solid conducts electricity in solid state but ionic solids do so only in molten state or in solution or metals conduct electricity through electrons and ionic substances through ions. Metallic solids are malleable and ductile while ionic solids are hard and brittle. 

Question 35. 
What is the formula of a compound in which the element Y forms ccp lattice and atoms of X occupy 1/ 3rd of tetrahedral voids? 
Answer: 
Formula is X₂Y₃.

Question 36. 
What is the formula of a compound in which the element Y forms ccp lattice and atoms of X occupy 2/ 3rd of tetrahedral voids?
Answer:  
Y atoms are N (No. of tetrahedral voids are 2N), No. of tetrahedral voids occupied by X are
\(\frac{2}{3} \times 2 \mathrm{~N}=\frac{4 \mathrm{~N}}{3}\)
X : Y = 4N : 3N

Question 37. 
What is the no. of atoms per unit cell (Z) in a body- centred cubic structure?
Answer:  
Contribution by the atoms present at eight corners
= 8 x 1/8 = 1
Contribution by the atoms present at centre = 1 
Total number of atoms present in unit cell = 1+1 = 2 

Question 38. 
What type of stoichiometric defect is shown by AgCl? 
Answer:  
AgCl shows Frenkel defect.

Question 39. 
What type of magnetism is shown by a substance if magnetic moments of domains are arranged in same. 
Answer:  
Ferromagnetism is shown by a substance if magnetic moments of domains are arranged in same direction.

Question 40. 
Give an example each of a molecular solid and an ionic solid.
Answer:  
Molecular solid → Iodine (12)
Ionic solid → Sodium chloride (NaCl)

Question 41. 
A metallic element crystallises into a lattice having a pattern of AB AB... and packing of spheres leaves out voids in the lattice. What type of structure is formed by this arrangement? 
Answer: 
Tetrahedral void is formed in AB AB... pattern. The hexagonal close packing (hcp) is formed in this ar- rangement.

Question 42. 
A metallic element crystallises into a lattice having a ABC ABC... pattern and packing of spheres leaves out voids in the lattice. What type of structure is formed by this arrangement?
Answer:  
Octahedral voids are formed in ABC ABC... pattern. The cubic close packing (ccp) is formed in this arrangement. 

Question 43. 
What type of Stoichiometric defect is shown by AgCl?
Answer:  
Frenkel defect.

Question 44. 
What type of stoichiometric defect is shown by NaCl?
Answer:  
Schottky defect is shown by Nacl. 

Question 45. 
Which ionic compound shows both Frenkel and Schottky defects?
Answer:  
Silver bromide (AgBr) shows both Schottky and Frenkel defect. 

Short Answer Type Questions:

Question  1. 
Explain how you can determine the atomic mass of an unknown metal if you know its mass density and the dimensions of unit cell of its crystal. 
Answer:
Suppose edge of the unit cell = 4 pm
Number of atoms present per unit cell = Z 
∴ Volume of unit cell = (a pm)³ 
= (a x 10^-10 cm)³ = a³ x 10^-30 cm³

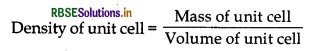
Mass of unit cell = Number of atoms in the unit cell x mass of each atom
= Z X m

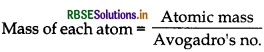
= \(\frac{\mathrm{M}}{\mathrm{N}_{\mathrm{A}}}\)
Substituting these values in equation (i), we get
Density of unit cell = \(\frac{\mathrm{Z} \times \mathrm{M}}{a^3 \times 10^{-30} \times \mathrm{N}_{\mathrm{A}}}\)
If a is in cm, d = \(\frac{\mathrm{Z} \times \mathrm{M}}{a^3 \times \mathrm{N}_{\mathrm{A}}} \mathrm{g} / \mathrm{cm}^3\)
∴ Molar mass can be calculated as
\(\mathrm{M}=\frac{d \times a^3 \times \mathrm{N}_{\mathrm{A}}}{\mathrm{Z}}\)

Question 2. 
Calculate the packing efficiency of a metal crystal for a simple cubic lattice.
Answer:
Percentage efficiency of packing of simple cubic lattice = 52.4%. 

Question 3. 
Define the following terms in relation to crystalline solids: 
(i) Unit cell 
(ii) Coordination number Give one example in each case. 
Answer:
(i) Unit cell: The smallest three dimensional portion of a complete space latice which when repeated over and again in different directions produces the complete space lattice is called the unit cell. 

(ii) Coordination number: The number of nearest spheres with which a particular sphere is in contact is called co-ordination number. Example: Co-ordination number of hexagonal (hcp) structures is 12. 

Question 4. 
The unit cell of an element of atomic mass 108 u and density 10.5 gcmis a cube with edge length, 409 pm. Find the type of unit cell of the crystal. (Given: Avogadro's constant 6.023 x10² mol^-1]
Answer:
We know that 

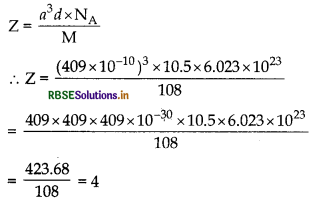
So it forms cubic closed packed (ccp) lattice or foc structure. 

Question 5. 
Explain the following terms with suitable examples: Ferromagnetism and Ferrimagnetism 
Answer:
Ferromagnetic solids: The solids which are strongly attracted by external magnetic field and do not lose their magnetism when the external field is removed are called ferromagnetic solids. The property, thus exhibited, is termed as ferromagnetism. Example: Fe, Co and Ni show ferromagnetism at room temperature. Ferrimagnetic solids: The solids which are expected to show large magnetism due to the presence of unpaired electrons but in fact have small net magnetic moment, are called ferrimagnetic solids. Example: Fe₂O, and ferrites.

Question 6. 
An element X crystalizes in f.c.c. structure, 208 g of it has 4.2832 X 10²⁴ atoms. Calculate the edge of the unit cell, if density of X is 7.2 g cm^-3 
Answer:
Z = 4(fcc) 
d = 7.2 g/cm³
a = ? 
4.2832 x 10²⁴ atoms have mass = 208 g 
6.022 x 10²³ atoms have mass
\(=\frac{208}{4.2832 \times 10^{24}} \times 6.022 \times 10^{23}\)
= 29.24 (at. mass)
\(a^3=\frac{\mathrm{Z} \times \mathrm{M}}{d \times \mathrm{N}_{\mathrm{A}}}=\frac{4 \times 29.24}{7.2 \times 6.022 \times 10^{23}}\)
= 269.6 x 10^-24 cm³
∴ a = 6.46 x 10^-8 cm = 646 A

Question 7. 
What is a semiconductor? Decribe the two main types of semiconductors.
Answer:
Semiconductor: The solid materials whose electrical conductivity lies between those of the typical metallic conductors and insulators are termed as seniconductors. The semiconductors possess conductivity in the range of 102 to 10-9 ohm-1 cm-1.
These are of two types: 
(a) n-type semiconductors: Doping of higher group element impurity forms n-type semiconductors, e.g. when 'As' is doped in 'Ge'. 
(b)p-type semiconductors: Impurity of lower groups forms election deficient bond in the structure. Electron deficiency develops to p-hole. 

Question 8. 
Account for the following:
1. Schottky defects lower the density of related solids. 
2. Conductivity of silicon increase on doping it with phosphorous.
Answer:

1. Schottky defect produced due to missing of equal number of cation and anion from lattice as a result of which the density of the lattice solid decreases.
2. The conductivity of silicon increases due to negatively charged extra electron of doped pentavalent phosphorus. 

Question 9. 
Aluminium crystallizes in an foc structure. Atomic radius of the metal is 125 pm. What is the length of the side of the unit cell of the metal? 
Answer:
For fcc, Formula: \(r=\frac{a}{2 \sqrt{2}}\)
r = 125 pm 
∴ a = \(2 \sqrt{2} r\) or a = \(2 \sqrt{2} \times 125\)
a = 2 x 1.414 x 125 = 353.5 pm 

Question 10. 
(a) Why does presence of excess of lithium makes LiCi crystals pink? 
(b) A solid with cubic crystal is made of two elements P and Q. Atoms of Q are at the corners of the cube and P at the body-centre. What is the formula of the compound?
Answer:
(a) This is due to metal excess defect due to anionic sites are occupied by unpaired electrons (F-centres). 
(b) As atoms of Q are present at the 8 centres of the cube, therefore number of atoms of Q in the unit cell
= 1/8 x 8 = 1
The atom Pis at the body centre 
∴ Number of atoms = 1 
Ratio of atoms P : Q = 1 : 1
Hence, the formula of the compound is PQ. 

Question 11. 
(a) What change occurs when AgCl is doped with CdCl₂? at type of semiconductor is produced silicon is doped with boron?
Answer:
(a) Impurity defect of ionic solids is produced when AgCl is doped with CdCl₂. Due to this defect vacancies are created that result in higher electrical conductivity of the solid. 
(b) p-type semi-conductor is obtained when silicon is doped with boron. 

Question 12. 
If NaCl is doped with 10^-3 mol percent SrCl₂, what will be the concentration of cation vacancies? (N_A = 6.02 x 10²³ mol^-1)
Answer:
10^-3 mol percent means 100 moles of NaCl are doped with 10^-3 moles of SrCl₂
∴ 1 mole of NaCl is doped with SrCl₂
\(=\frac{10^{-3}}{100}\)
= 10^-5 mol
Since each Sr?+ ion introduces one cation vacancy 
∴ Concentration of cation vacancies
= 10^-5 mol/mol of NaCl 
= 10^-5 X 6.02 x 10²³ mol^-1
= 6.02 x 10¹⁸ mol^-1 

Question 13. 
What is a semiconductor? Describe the two main types of semiconductors and contrast their conduction mechanism.
Answer:
Semiconductor: The solids which have intermediate conductivities between metals and non-metals i.e. between 10-6 to 104 m-1 are called semiconductors. Example: Germanium and Silicon. 
Main types of semiconductors are of two types: 

1. Intrinsic semiconductor: These are insulators at room temperature and become semiconductors when temperature is raised. 
2. Extrinsic semiconductor: p-type semiconductor ntype semiconductor These are formed by dopping impurity of lower or higher group. 

These are subdivided into two types: 

1. p-type semiconductor : When a silicon crystal is doped with atom of group-13 elements like B, Al, Ga etc, the atom forms only 3 covalent bonds with the Si atom and 4th missing electron creates a hole which conducts electricity.
2.  n-type semiconductor : When a silicon crystal is doped with atoms of group-15 elements like P, As etc, then only four of the five valence electrons of each impurity atom participate in 4 covalent bond forma- tion and 5th e conducts electricity.

Question 14. 
A compound forms hcp structure. What is the total number of voids in 0.5 mol of it? How many of these are tetrahedral voids?
Answer:
No. of atoms in the hep
= 0.5 x 6.022 x 10^-23
= 3.011 × 10²³
No. of octahedral voids
No. of atoms in packing
= 3.011 × 10²³
= 2 x  No. of atoms in packing 
= 2 x 3.011 × 10²³
= 6.022 x 10²³
∴ Total no. of voids
= 3.011 × 10²³ + 6.022 × 10²³ 
= 9.033 x 10²³

Question 15. 
An element crystallizes in a structure haing fcc unit cell of an edge 200 pm. Calculate the density if 200 g of this element contains 24 x 10²³ atoms.
Answer:
24 x 10²³ atoms of an element have mass = 200 g
∴ 6.022 × 10²³ atoms of an element have mass
= \(\frac{200}{24 \times 10^{23}}\) x 6.022 x 10²³ = 50.18 g
Given: a = 200 pm = 200 x 10^-12 cm, 
Z = 4 (For fcc), 
M = 50.18 g
Using the formula: 

Question 16. 
An element with density 11.2 g cm³ forms a f.c.c. lattice with edge length of 4 × 10^-8 cm. Calculate the atomic mass of the element.
(Given: N_A = 6.022 × 10²³ mol^-1)
Answer:
Given:
d = 11.2gcm^-3, a
For fcc lattice, Z = 4
= 4 × 10^-8 cm
Using formula, 

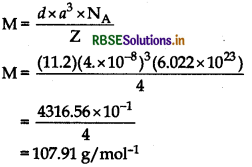
Question 17. 
Examine the given defective crystal

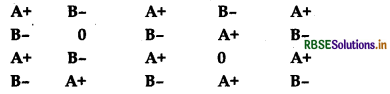
Answer the following questions: 
1. What type of stoichiometric defect is shown by the crystal? 
2. How is the density of the crystal affected by this defect? 
3. What type of ionic substances show such defect?
Answer:

1. Schottky defect
2. Density of the crystal decreases 
3. NaCl (lonic solids having approximate equal size of cations and anions) 

Question 18. 
An element with density 2.8 gcm forms af.c.c. unit cell with edge 4 x 10 cm. Calculate the molar mass of the element.
(Given: NA = 6.022 x 10²³ mol^-1) 
Answer:
Using formula: 
\(d=\frac{\mathrm{Z} \times \mathrm{M}}{a^3 \times \mathrm{N}_0}\)
for fcc Z = 4

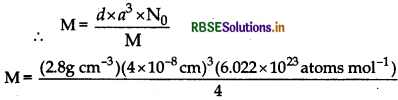
∴ Molar mass,
\(\mathrm{M}=\frac{1079.1424}{40}\)
= 26.978 g/mol 

Question 19. 
1. What type of non-stoichiometric point defect is responsible for the pink colour of LICl? 
2. What type of stoichiometric defect is shown by NaCl?
Answer:

1. This is due to metal excess defect due to anionic vacancies in which the anionic sites are occupied by unpaired electrons (F-centres).
2. Schottky defect is shown by NaCl. 

Question 20. 
How will you distinguish between the following pairs of terms: 
(i) Tetrahedral and octahedral voids
(ii) Crystal lattice and unit cell 
Answer:
(i) 

Tetrahedral voids	Octahedral voids
It is much smaller than the size of spheres in the packing.	Size is much larger than tetrahedral voids.
Each tetrahedral void is surrounded by 4 spheres. Hence, coordination no. is 4	Each octahedral void is surrounded by 6 spheres. Hence, its coordination no. is 6 .

(ii) A reuglar arrangement of the constituent particles of a crystal in a three dimensional space is called crystal lattice. The smallest three dimensional portion of a complete crystal lattice, which when repeated over and again in different directions produces the complete crystal lattice is called the unit cell. 

Question 21. 
1. Write the type of magnetism observed when the magnetic moments are oppositively aligned and cancel out each other. 
2. Which stoichiometric defect does not change the density of the crystal?
Answer:

1. Diamagnetism is observed when the magnetic moments are oppositively aligned and cancel out each other. 
2. Frenkel defect does not change the density of the crystal. 

Question 22. 
1. Write the type of magnetism observed when the magnetic moments are aligned in parallel and antiparallel directions in unequal numbers. 
2. Which stoichiometric defect decreases the density of the crystal?
Answer:

1. Ferrimagnetism is observed.
2. Schottky defect decreases the density of the crystal.

Question 23. 
Define the following terms: 
1. n-type semiconductor
2. Ferrimagnetism 
Answer:

1. n-type semiconducor: When Si/Ge is doped with group 15 element 
2. Ferrimagnetism: When magnetic domains are aligned in parallel and anti-parallel directions in un equal numbers. 

Question 24. 
Explain the following terms with suitable examples:
1. Frenkel defect 
2. F-centres 
Answer:

1. Frenkel defect : The defect in which the smaller ion/cation is dislocated to a nearby interstitial site. Example: Silver halides, ZnS. 
2. F-centres : The anion vacancy occupied by an electron is called F-centre in Alkali metal halides. Examples: NaCl, KCl, LICl. 

Question 25. 
Calculate the number of unit cells in 8.1 g of aluminium if it crystalizes in a face-centred cubic (f.c.c.) structure. (Atomic mass of Al = 27 g mol^-1)
Answer:
1 mole of Aluminium = 27 g 6.022 x 10²³ 
Hence, No. of atoms present in 27 g of Al
\(=\frac{6.022 \times 10^{23}}{27}\)
As f.c.c. unit cell contains 4 atoms 
∴ No. of f.c.c. unit cells present
\(=\frac{6.022 \times 10^{23} \times 8.1}{27 \times 4}\)
= 0.45165 x 10²³
= 4.5165 x 10²² 

Question 26. 
Iron has a body centred cubic unti cell with a cell edge of 286.65 pm. The density of iron is 7.87 gcm Use this information to calculate Avogadro's num
ber (At. mass of Fe = 56 g mol^-1). 
Answer:

 ∴ Avogadro's number
NA = 6.022 x 10²³ 

Question 27. 
Silver crystallises with face-centred cubic unit cells. Each side of the unit cell has a length of 409 pm. What is the radius of an atom of silver? (Assume that each face atom is touching the four corner atoms.)
Answer:
Given: a = 409 pm r = ?
For foc unit cell, the formula is
\(r=\frac{a}{2 \sqrt{2}}\)
or
\(r=\frac{409}{2 \sqrt{2}}=\frac{409}{2 \times 1.414}=\frac{409}{2.828}\)
∴ r = 144.62 
∴ Radious of an atom of silver = 144.62 pm

Question 28. 
The well known mineral fluorite is chemically calcium fluoride. It is known that in one unit cell of this mineral there are 4 Ca²⁺ ions and 8 Fions and that Ca²⁺ ions are arranged in a foc lattice. The Fions fill all the tetrahedral holes in the face centred cubic lattice of Ca²⁺ ions. The edge of the unit cell is 5.46 x 10^-8 cm in length. The density of the solid is 3.18 g cm-3 . Use this information to calculate Avogadro's number (Molar mass of CaF2 = 78.08 g mol-?).
Answer:
Given: Edge of the unit cell (a) = 5.46 x 10^-8 cm
Density (d) = 3.18 gcm^-3 
According to the formula:

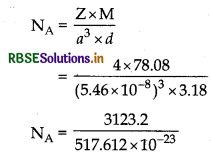
= 6.033 x 10²³ 

Question 29. 
The density of copper metal is 8.95 g cm^-3 . If the radius of copper atom is 127.8 pm, is the copper unit cell a simple cubic, a body-centred cubic or a face centred cubic structure? (Given: At mass of Cu = 63.54 g mol^-1 and NA = 6.02 x 10²³ mol-¹)
Answer:
If copper atom were simple cubic:
a = 2 x r = 2 x 127.8 pm
= 255.6 pm = 255.6 x 10^-10 cm 
Z = 1
\(d=\frac{\mathrm{Z} \times \mathrm{M}}{a^3 \times \mathrm{N}_{\mathrm{A}}}\)
\(\frac{1 \times 63.54}{\left(255.6 \times 10^{-10}\right)^3 \times\left(6.02 \times 10^{23}\right)}\)
d = 6.34 g cm^-3 
Actual density = 8.95 g cm^-3 
Hence, copper atom is not body centred 
If copper atom were body-centred:
\(a=\frac{4 r}{\sqrt{3}}=\frac{4 \times 127.8}{1.732}\)
= 295.19 pm
Z = 2
\(\begin{aligned} d &=\frac{\mathrm{Z} \times \mathrm{M}}{a^3 \times \mathrm{N}_{\mathrm{A}}} \\ &=\frac{2 \times 63.54}{\left(295.15 \times 10^{-10}\right)^3 \times 6.02 \times 10^{23}} \end{aligned}\)
∴ d = 8.21 g cm^-3
Hence, copper atom is not body centred 
If copper atom were face-centred:
a = 2√2
or
a = 2 × 1.414 x 127.8 pm 
= 361.4 pm
= 361.4 × 10^-10 cm
\(d=\frac{\mathrm{Z} \times \mathrm{M}}{a^3 \times \mathrm{N}_{\mathrm{A}}}\)
= \(\frac{4 \times 63.54}{\left(361.4 \times 10^{-10}\right)^3 \times 6.02 \times 10^{23}}\)
d = 8.94 cm^-3.

Question 30. 
Silver crystallizes in face-centred cubic unit cell. Each side of this unit cell has a length of 400 pm. Calculate the radius of the silver atom. (Assume the atoms just touch each other on the diagonal across the face of the unit cell. That is each face atom is touching the four corner atoms.) 
Answer:
Given:
a = 400 pm, r = ?
For fcc unit cell:
\(r=\frac{a}{2 \sqrt{2}}\)
or
\(=\frac{400}{2 \times 1.4142}=\frac{400}{2.828}\)
∴ r = 141.4
∴ Radius of the silver, r = 141.4 pm

Question 31. 
The density of lead is 11.35 g cm³ and the metal crystallizes with fcc unit cell. Estimate the radius of lead atom. (At. Mass of lead = 207 g mol^-1  and NA = 6.02 × 10²³ mol^-1)
Answer:
Given: d = 11.35 g cm^-3
According to the formula
\(d=\frac{\mathrm{Z} \times \mathrm{M}}{a^3 \times \mathrm{N}_{\mathrm{A}}}\)
or
\(a^3=\frac{\mathrm{Z} \times \mathrm{M}}{d \times \mathrm{N}_{\mathrm{A}}}\)
For fcc lattice, Z = 4
\(a^3=\frac{4 \times 207 \mathrm{~g} \mathrm{~mol}^{-1}}{11.35 \mathrm{~g} \mathrm{~cm}^{-3} \times 6.02 \times 10^{23} \mathrm{~mol}^{-1}}\)
or
\(a^3=\frac{828}{68.327 \times 10^{23}}\)
= 12.118 x 10²³
or
\(a=\sqrt[3]{1.212 \times 10^{-22}} \mathrm{~cm}^3\)
∴ a = 4.95 x 10^-8 cm
For fcc unit cell,
\(r=\frac{a}{2 \sqrt{2}}\)
or
\(r=\frac{4.95 \times 10^{-8}}{2 \times 1.414}=\frac{4.95 \times 10^{-8}}{2.828}\)
∴ Radius,
r = 1.75 x 10^-8 cm = 175 pm.

Question 32. 
Tungsten crystallizes in body centred cubic unit cell. If the edge of the unit cell is 316.5 pm, what is the radius of tungsten atom?
Answer:
For bcc, unit cell: 
radius, \(r=\frac{\sqrt{3} a}{4}\)
(∵ a = 316.5 pm)
\(=\frac{\sqrt{3} \times 316.5 \mathrm{pm}}{4}\)
= \(\frac{1.732 \times 316.5 \mathrm{pm}}{4}\)
= 137 pm.

Question 33. 
Iron has a body centred cubic unit cell with a cell dimension of 286.65 pm. The density of iron is 7.874 gcm^-3. Use this information to calculate Avogadro's number. (At. mass of Fe = 55.845 u) 
Answer:
\(d=\frac{\mathrm{Z} \times \mathrm{M}}{a^3 \times \mathrm{N}_{\mathrm{A}}}\)
For bcc, latice z = 2
[bcc = body centred cubic]

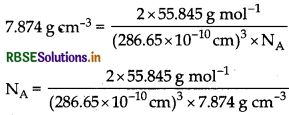
∴ Avogadro's number NA = 6.02 x 10²³ mol^-1

Question 34. 
Copper crystallises with face centred cubic unit cell. If the radius of copper atom is 127.8 pm, calculate the density of copper metal. (Atomic mass of Cu = 63.55 u and Avogadro's number NA = 6.02 x 10²³ mol^-1)
Answer:
In fcc, lattice, Z = 4 atoms [fcc = face centred cubic)
Formula: 
\(d=\frac{\mathrm{Z} \times \mathrm{M}}{a^3 \times \mathrm{N}_{\mathrm{A}}}\)
fcc latice for copper a = \(2 \sqrt{2} r\)
a³ = \(2 \sqrt{2} r\)
⇒ a³ = 8 x \(2 \sqrt{2} r\) (1.278 x 10⁸ cm)³
⇒ a³ = 4.723 x 10^-23 cm³

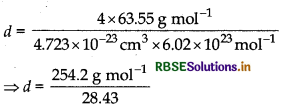
= 8.94 g cm^-3

Question 35. 
Iron has a body centred cubic unit cell with the cell dimension of 286.65 pm. Density of iron is 7.87 g cm. Use this information to calculate Avogadro's number. (Atomic mass of Fe = 56.0 u) 
Answer:
\(d=\frac{\mathrm{Z} \times \mathrm{M}}{a^3 \times \mathrm{N}_{\mathrm{A}}}\)
for bcc = 2
\(\mathrm{N}_{\mathrm{A}}=\frac{\mathrm{Z} \times \mathrm{M}}{a^3 \times d}=\frac{2 \times 56 \mathrm{~g} \mathrm{~mol}^{-1}}{\left(286.65 \times 10^{-10}\right)^3 \times 7.87 \mathrm{~cm}^{-3}}\)
= 6.043 x 10²³ mol^-1

Question 36. 
(a) Some of the glass objects recovered from ancient monuments look milky instead of being transparent. Why?
(b) Iron (II)oxide has a cubic structure and each side of the unit cell is 5 Å. If density of the oxide is 4gcm 3 calculate the number of Fe²⁺ and O^2- ions present in each unit cell. (Atomic mass : Fe = 56 u, O = 16 u; Avagadaro's number = 6.023 x 10²³ mol^-1] 
Answer:
(a) Some of the glass objects found from ancient monuments look to be milky in appearance because of crystallisation of glass. 
(b) Volume of unit cell 
a³ = (5A) = (5 x 10^-8)³
= 1.25 x 10^-22cm
Density of FeO = 4g cm^-3 
 Mass of unit cell= Volume x Density
= 1.25 x 10^-22 x 4g = 5 x 10^-22 g
Mass of FeO molecule per unit cell
= \(\frac{5 \times 10^{-22} \mathrm{~g}}{1.195 \times 10^{-22} \mathrm{~g}}\) = 4.19 = 4
Thus 4Fe⁺², 4O^-2 will be present in each unit cell. 

Question 37. 
(a) What are intrinsic semi-conductors? Give an example. 
(b) What is the distance between Na⁺ and Clions in NaCl crystal if its density is 2.165 g cm-? [Atomic Mass of Na = 23u, Cl = 35.5u; Avogadro's number = 6.023 x 10²³]
Answer:
(a) Intrinsic semi-conductors: These are insulators at room temperature and become semi-conductors when temperature is raised. Example: silicon and germanium.
(b) Applying the formula

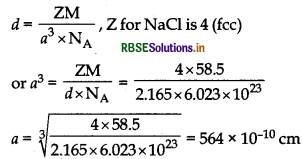
a = 2 x distance between Na⁺ and Cl^- ions 
∴ Distance between Na⁺ and Cl^- ion

= \(\frac{564 \times 10^{-10}}{2}\)
= 282 pm.

Question 38. 
(a) What type of semiconductor is obtained when silicon is doped with boron?
(b) What type of magnetism is shown in the following alignment of magnetic moments?

(c) What type of point defect is produced when AgCl is doped with CdCl₂?
Answer:
(a) p-type semi-conductor is obtained when silicon is doped with boron.
(b) Ferromagnetism is shown when the alignment of magnetic movements will be

(c) Impurity defect of inonic solids is produced when AgCl is doped with CdCl₂. Due to this defect vacancies are created that result in Higher electrical conductivity of the solid. 

Question 39. 
An element occurs in bcc structure. It has a cell edge length of 250 pm. Calculate the molar mass if its density is 8.0 g cm . Also calculate radius of an atom of this element.
Answer:
Given for bcc structure , Z = 2
Edge of the unit cell, a = 250 pm
Density of the element d = 8.0 g/cm3
M = ?
r = ?
Using the formula

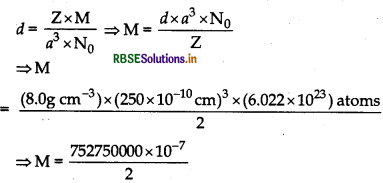
∴ M = 37.6 g mol^-1

For bcc, \(a=\frac{4 r}{\sqrt{3}} \Rightarrow 250=\frac{4 r}{\sqrt{3}}\)

∴ \(r=\frac{250 \times 1.73}{4}\) = 108.25 pm

Question 40. 
Iron (II)oxide has a cubic structure and each unit cell has a size of 5 A. If density of this oxide is 4 g em calculate the number of Fe²⁺ and O₂ ions present in each unit cell. (Atomic mass of Fe = 56, O = 16, NA = 6.023 x 10²³ and 1 A = 10^-8 cm) 
Answer:
Given p = 4 g cm^-3
a = 5A = 5 x 10^-8 cm M = 72 g / mol Z = ?

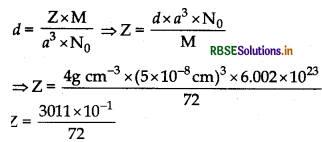
= 4.18 = 4
There are four formula units of FeO present per unit cell. Hence it has face-centred cubic lattice where each Fe²⁺ and O^2- are four in number.

Question 41.
Niobium crystalizes in body centred cubic structure, if its density is 8.55 g cm^-3, calculate atomic radius of niobium given its atomic mass 93 u.
Answer:
Given d = 8.55 gcm^-3
M = 93 g/mol^-1
Z = 2 (for bcc) a = ?
Using formula
\(a^3=\frac{\mathrm{M} \times \mathrm{Z}}{d \times \mathrm{N}_{\mathrm{A}} \times 10^{-30}}\)
x = (3.61)1/3
log x = 1/3 log 36.1 = 1/3 x 1.1575 = 0.519
⇒  x log 0.519 = 3.304

\(\Rightarrow a^3=\frac{93 \mathrm{~g} \mathrm{~mol}^{-1} \times 2}{8.55 \mathrm{~g} \mathrm{~cm}^{-3} \times 6.022 \times 10^{23} \mathrm{~mol}^{-1} \times 10^{-30}}\)
= 3.61 x 107 = 361 x 106
a = (36.1)1/3 x 102 pm 
∴ a = 3.304 x 102 pm = 33.04 pm
for bcc r₁ = \(\frac{\sqrt{3}}{4} a=\frac{\sqrt{3}}{4} \times 330.4\) = 143.1 pm

Question 42.
The density of copper is 8.95 g cm^-3 it has a face centred cubic structure. What is the radius of copper atom? (Atomic mass Cu = 63.5 g mol^-1, NA = 6.02 x 10²³ mol^-1)
Answer:
Using \(d=\frac{\mathrm{Z} \times \mathrm{M}}{a^3 \times \mathrm{N}_{\mathrm{A}}}\)

[Given d = 8.95 g cm^-3 , For fcc, Z = 4]

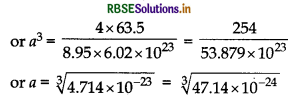
= 3.613 x 10^-8 cm.

Question 43.
Iron has a body centred cubic unit cell dimensions of 286.65 pm. The density of iron is 7.874 g cm^-3. Use this information to calculate Avogadro's number. (Atomic mass
of Fe = 55.84 g mol^-1)
Answer:
a = 286.65 pm = 286.65 x 10^-10
d = 7.87 g cm^-3 M = 56 g mol^-1
Z = 2 NA = ?
Using formula

∴ Avogadro's number NA = 6.022 × 10²³

Question 44. 
Iron has a body centred cubic unit cell with a cell dimension of 286.65 pm. The density of iron is 7.874 gcm³. Use this information to calculate Avogadro's number. (Gram atomic mass of Fe = 55.84 g mol^-1)
Answer:
a = 286.65 pm = 286.65 x 10^-10 cm
M = 55.84 g mol^-1
d = 7.874 gcm³

substuting the value in the expression


Question 45. 
An element with molar mass 27 g mol^-1 forms a cubic unit cell with edge length 4.05 x 10 cm. If its density is 2.7 g cm^-3, what is the nature of the cubic unit cell? 
Answer:

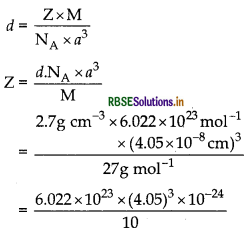
= 6.022 x 10^-22 x 66.43 = 4.0004 = 4
It has Face centred cubic cell/fcc.

Question 46. 
Examine the given defective crystal:

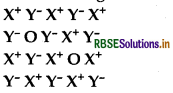
Answer the following questions:
1. Is the above defect stoichiometric or non-stoichio- metric?
2. Write the term used for this type of defect. Give an example of the compound which shows this type of defect.
3. How does this defect affect the density of the crystal?
Answer:

1. It is stoichiometric defect.
2. Schottky defect, e.g. NaCl.
3. Density of crystal decreases. 

Question 47. 
Define the following:
1. Schottky defect 
2. Frenkel defect 
3. F-centre
Answer:

1. Schottky defect: If in an ionic crystal of type A+ B - equal number of cations and anions are missing from their lattice sites so that the electrical neutrality is main- tained, it is called Schottky defect.
2. Frenkel defect: If an ion leaves its site from its lattice site and occupies the interstitial site and main- tains electrical neutrality, then it is called Frenkel de- fect.
3. F-centre: The centres which are created by trap- ping of electrons in anionic vacancies and which are responsible for imparting colour to the crystals are called F-centres. (F = Fabre)

Question 48. 
Silver crystallises in fcc lattice. If edge length of the unit cell is 4.077 x 10^-8 cm, then calculate the radius of silver atom.
Answer:
Given: a = 4.077 × 10^-8 cm r = ? for fcc lattice Using
formula,
Radius(r)

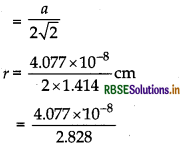
r = 1.441 x 10⁸ cm.

Question 49. 
An element crystallizes in a f.c.c. lattice with cell edge of 250 pm. Calculate the density if 300 g of this ele- ment contains 2 x 10²⁸ atoms.
Answer:
Given:
a = 250 pm = 250 × 10^-10 cm
Z = 4 (for fcc)
M = ? d = ?
Using formula:
\(d=\frac{\mathrm{Z} \times \mathrm{M}}{a^3 \mathrm{~N}_{\mathrm{A}}}\)
∵ 2 x 10²⁴ atoms of an element have mass = 300 g
∴  6.022 × 10²³ atoms of an element have mass
= \(\frac{300 \times 6.022 \times 10^{23}}{2 \times 10^{24}}\) = 90.33 g
Now
M = 90.33 g.

Question 50. 
An element crystallizes in a b.c.c. lattice with cell edge of 500 pm. The density of the element is 7.5g cm³. How many atoms are present in 300 g of the element? 
Answer:
Given: For b.c.c. structure, z = 2
Edge of the unit cell, a = 500 pm = 500 x 10^-10 cm 
Density d = 7.5 g cm^-1
Using the formula,

∵ 282.28 g of the element contains = 6.022 × 10²³ atoms
∵ 300 g of the element contains
\(\begin{aligned} &=\frac{6.022 \times 10^{23}}{282.28} \times 300 \\ &=\frac{1806.6}{282.28} \times 10^{23} \end{aligned}\)
= 6.40 x 10²³ atoms

Question 51. 
If NaCl is doped with 10^-3 mol % of SrCl₂, what is the concentration of cation vacancies?
Answer:
Concentration of SrCl₂ = 10^-3 mol %  = 10^-3/100 mol = 10^-5 mol
1 mol of NaCl on doping process = 6.022 × 10²³ cation vacancies
Therefore, 10-5 mol of NaCl.on dopping produces = 6.022 x 10²³ x 10^-5 = 6.022 x 10¹⁸ cation vacancies 

Question 52. 
Silver crystallises in f.c.c. lattice. If edge length of the cell is 4.07 × 10^-8 cm and density is 10.5 g cm³, calcu- late the atomic mass of silver. 
Answer:

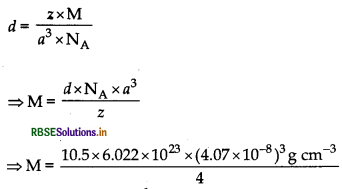
⇒ M = 106.6 g mol^-1

Question 53. 
(a) Based on the nature of intermolecular forces, clas- sify the following solids: Silicon carbide, Argon 
(b) ZnO turns yellow on heating. Why?
(c) What is meant by groups compounds? Give an example. 
Answer:
(a) Silicon carbide is a covalent or network solid while Argon is a non-polar molecular solid.
(b) ZnO shows metal excess defect due to presence of extra cations, i.e. Zn²⁺ ions in interstitial sites which on heating changes into yellow due to loss of oxygen.

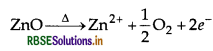
(c) Group 12 - 16 compounds are imperfect covalent compounds in which the ionic character depends on the electronegativities of the two elements, e.g. ZnS, CdS, etc.

Question 54. 
(a) Based on the nature of intermolecular forces, clas- sify the following solids: Benzene, Silver.
(b) AgCl shows Frenkel defect while NaCl does not. Give reason.
(c) What type of semiconductor is formed when Ge is doped with Al? 
Answer:
(a) Benzene-Molecular solid (non-polar)
Silver - Metallic solid
(b) Due to intermediate radius of AgCl, the size of Ag⁺ is smaller than larger Na⁺ ion of NaCl so it can easily occupy interstitial spaces and shows Frenkel defect. 
(c) p-type semiconductor is formed when Ge is doped with Al.

Question 55. 
(a) Based on the nature of intermolecular forces, classify the following solids: Sodium sulphate, Hydrogen.
(b) What happens when CdCl, is doped with AgCI? 
(c) Why do ferrimagnetic substances show better magnetism than antiferromagnetic substances? 
Answer:
(a) Sodium sulphate - Ionic solid
Hydrogen - Molecular solid (non-polar)
(b) Cd²⁺ ion is dipositive and therefore addition of one Cd²⁺ ion results in the loss of two Ag⁺ ions from the lattice. But out of 2 holes obtained, one is occupied by Cd²⁺ ion and one left empty. Hence, addition of CdCl₂ results in an impurity defect with cation vacancy. 
(c) Inferrimagnetism domains/magnetic moments are aligned in opposite direction in unequal numbers while in antiferromagnetic substances, the domains align in opposite direction in equal numbers so they cancel magnetic moments completely, i.e., net magne- tism is zero.

Question 56. 
An element crystallises in b.c.c. lattice with cell edge of 400 pm. Calculate its density if 500 g of this ele- ment contains 2.5 x 10²⁴ atoms. 
Answer:
Given: a 400 pm = 400 x 10^-10 cm
Z = 2 (for bcc)
M = ? d = ?
Using formula,
\(d=\frac{\mathrm{Z} \times \mathrm{M}}{a^3 \times \mathrm{N}_{\mathrm{A}}}\)
∵ 2.5 x 10²⁴ atoms of an element have mass = 500 g
∴ 6.022 × 2023 atoms of an element have mass
\(=\frac{500 \times 6.022 \times 10^{23}}{2.5 \times 10^{24}}\)
∴ M = 120.44 g
Substituting all values in the formula:

d = 6.25 g cm^-3

Question 57. 
An element crystallises in fcc lattice with cell edge of 400 pm. Calculate its density if 250 g of this element contain 2.5 x 10²⁴ atoms.
Answer:
Given: a = 400 pm = 400 x 10^-10 cm
Z = 4 (for fcc), M = ? d = ?
Using formula,
\(d=\frac{\mathrm{Z} \times \mathrm{M}}{a^3 \times \mathrm{N}_{\mathrm{A}}}\)
∵ 2.5 x 10²⁴ atoms of an element have mass = 250 g 
∴ 6.022 x 10²³ atoms of an element have mass
\(=\frac{250 \times 6.022 \times 10^{23}}{2.5 \times 10^{24}}\)
M = 60.22 g
Substituting all values in formula:
\(\begin{aligned} d &=\frac{4 \times 60.22}{\left(400 \times 10^{-10}\right)^3 \times 6.022 \times 10^{23}} \\ &=\frac{240.88}{38.5408} \end{aligned}\)
d = 6.25 g cm^-3.

Question 58. 
An element crystallises in bcc lattice with cell edge of 400 pm. Calculate its density if 250 g of this element contains 2.5 x 1024 atoms.
Answer:
Given:
a = 400 pm = 400 × 10^-10 cm 
Z = 2(for bcc), M = ?,d = ?
Using formula,
\(d=\frac{\mathrm{Z} \times \mathrm{M}}{a^3 \times \mathrm{N}_{\mathrm{A}}}\)
∵ 25 x 10²⁴ atoms of an element have mass = 250 g 
\(=\frac{250 \times 6.022 \times 10^{23}}{2.5 \times 10^{24}}\)
∴ M = 60.22 g
Substituting all values in formula:
\(d=\frac{2 \times 60.22}{\left(400 \times 10^{-10}\right)^3 \times 6.022 \times 10^{23}}\)
= \(\frac{120.44}{38.5408}\)
∴ d = 3.125 g cm^-3.

Question 59. 
An element exists in bec lattice with a cell edge of 288 pm. Calculate its molar mass if its density is 7.2 g/cm³.
Answer:
Given: Cell edge, a = 288 pm = 288 x 10^-10 cm
Density, d = 7.2g/cm³
For bec formula, units per cell Z = 2, M = ?
Using formula and substituting values.

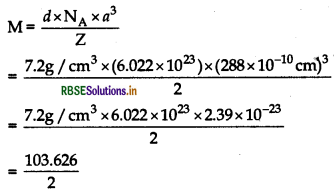
∴M = 51.8 g mol^-1

Long Answer Type Questions:

Question 1. 
(a) An element has an atomic mass 93 g mol^-1 and density 11.5 g cm^-3 If the edge length of its unit cell is 300 pm, identify the type of unit cell.
(b) Write any two differences between amorphous solids and crystalline solids.
Answer:
(a) Given:
Using formula,
M = 93 g mol^-1; p = 11.5 g cm^-3; a = 300 pm = 300 x 10^-10 cm
= 3 x 10^-8 cm
Using formula

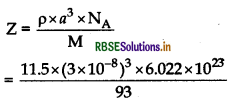
As the number of atoms present in given unit cells are coming nearly equal to 2, hence the given units cell is body centred cubic unit cell (BCC).

Amorphous solids	Crystaline solids
1. They are isotropic, i.e. they will show same value of all physical properties in all directions.	1. They are anisotropic, i.e value of physical properties will be different when measựred along different directions.
2. They have short range order.	2. They have long range order.

Question 2. 
(a) Calculate the number of unit cells in 8.1 g of aluminium if it crystallizes in a f.c.c. structure. (Atomic mass of A1 = 27 g mol^-1)
(b) Give reasons:
(i) In stoichiometric defects, NaCl exhibits Schottky defect and not Frenkel defect.
(ii) Silicon on dopping with Phosphorous form n-type semiconductor.
(iii) Ferrimagnetic substances show better magne- tism than antiferromagnetic substances.
Answer:
(a) Given:
Mass of A₁ = 8.1,
Atomic mass of A₁ = 27 g mol^-1 
No. of atoms = n x 6.022 × 10²³
= \(\frac{8.1}{27}\) x 6.022 × 10²³ 
= 0.3 × 6.022 × 10²³ 
= 1.8066 × 10²³
Since one f.c.c. unit cell has 4 atoms
∴ No of unit cells = \(\frac{1.8066 \times 10^{23}}{4}\)
= 4.5 × 10²² unit cells

(b) (i) Schottky defect is shown by the ionic solids having very small difference in their cathonic and anionic radius whereas Frenkel defect is shown by ionic sol- ids having large difference in their cationic and an- ionic radius. NaCl exhibits Schottky defect because radius of both Na⁺ and Cl^- have very small difference. 

(ii) Phosphorous is pentavalent that is it has 5 valence electrons, an extra electron results in the formation of n-type semi conductors on doping with Silicon. The conductivity is due to presence of extra electrons.

(iii) In antiferromagnetic substance the magnetic mo- ments of domains are half aligned in one direction and remaining half in opposite direction in the pres- ence of magnetic field so magnetic moment will be zero while in ferrimagnetic substances the magnetic moments of domains are aligned in parallel and anti- parallel directions in unequal numbers, hence shows some value of magnetic moment.

COMPETITION CORNER:

Question 1. 
The ionic rodii of A and B ions are 0.98 × 10^-10 m and 1.81 x 10^-10 m respectively. The coordination number of each ion in AB is:
(a) 6
(b) 4
(c) 8
(d) 2
Answer:
(a) 6

Question 2. 
Which of the following metal is crystallised in simple cubic structure?
(a) Po
(c) Ni
(b) Cu
(d) Fe
Answer:
(a) Po

Question 3. 
The correct statement in relation to defect in crystal line solids is:
(a) The density of crystalline solids is not affected by Schottky defect.
(b) Frenkel defect decreases the density of crystalline solid.
(c) Frenkel defect is dislocation defect.
(d) Frenkel defect is found in halides of alkali metals. 
Answer:
(c) Frenkel defect is dislocation defect.

Question 4. 
If pressure increases on NaCl structure then its co- ordination number will:
(a) increases
(c) remains same
(b) decreases
(d) (b) or (c)
Answer:
(a) increases

Question 5. 
Copper is crystallised in fcc structure with edge length of unit cell 361 pm, the atomic radius of copper is:
(a) 108 pm
(b) 127 pm
(c) 157 pm
(d) 181 pm
Answer:
(b) 127 pm

Question 6. 
Empty space in lattice unit cell is:
(a) 26%
(b) 48%
(c) 23%
(d) 32%
Answer:
(d) 32%

Question 7. 
The arrangement of X" ions on A ions in a solid AX is given in figure. If radius of X is 250 pm, then radius of A will be:
(a) 104 pm
(c) 183 pm
(b) 125 pm 
(d) 57 pm
Answer:
(a) 104 pm

Question 8. 
The number of carbon atoms in per unit cell of diamond will be:
(a) 1
(b) 4
(c) 8
(d) 6
Answer:
(c) 8