RBSE Class 10 Science Important Questions Chapter 10 प्रकाश - परावर्तन तथा अपवर्तन

Rajasthan Board RBSE Class 10 Science Important Questions Chapter 10 प्रकाश - परावर्तन तथा अपवर्तन Important Questions and Answers.

RBSE Class 10 Science Chapter 10 Important Questions प्रकाश - परावर्तन तथा अपवर्तन

वस्तुनिष्ठ प्रश्न

प्रश्न 1. 
प्रकाश का वेग सर्वाधिक होता है:
(क) काँच में
(ख) पानी में 
(ग) हवा में
(घ) निर्वात में 
उत्तर:
(घ) निर्वात में 

प्रश्न 2. 
प्रकाश के अपवर्तन की क्रिया में कौनसी भौतिक राशि अपरिवर्तित रहती है:
(क) आवृत्ति
(ख) वेग 
(ग) तरंगदैर्घ्य
(घ) इनमें से कोई नहीं 
उत्तर:
(क) आवृत्ति

प्रश्न 3. 
किसी समतल दर्पण पर प्रकाश की किरण अभिलम्बवत् आपतित होती है तो परावर्तन कोण का मान होता है:
(क) 90°
(ख) 180° 
(ग) 0°
(घ) 45° 
उत्तर:
(ग) 0°

प्रश्न 4. 
अवतल लैंस के सामने रखी वस्तु का प्रतिबिम्ब सदैव होता है:
(क) आभासी व सीधा
(ख) वास्तविक एवं सीधा 
(ग) काल्पनिक एवं उल्टा 
(घ) वास्तविक एवं उल्टा 
उत्तर:
(क) आभासी व सीधा

प्रश्न 5. 
डायप्टर मात्रक है:
(क) फोकस दूरी का
(ख) आवर्धन का 
(ग) लैंस की शक्ति का 
(घ) विभेदन क्षमता का 
उत्तर:
(ग) लैंस की शक्ति का 

प्रश्न 6. 
एक जरा दृष्टि दोष वाला मनुष्य दो लैंसों वाला चश्मा लगाता है, इनमें -
(क) ऊपर वाला उत्तल लैंस एवं नीचे वाला अवतल लैंस होगा। 
(ख) नीचे वाला उत्तल लैंस एवं ऊपर वाला अवतल लैंस होगा। 
(ग) दोनों उत्तल लैंस लेकिन भिन्न - भिन्न फोकस दूरी के।
(घ) दोनों अवतल लैंस लेकिन भिन्न - भिन्न फोकस दूरी के। 
उत्तर:
(ख) नीचे वाला उत्तल लैंस एवं ऊपर वाला अवतल लैंस होगा। 

प्रश्न 7. 
धुएँ के आर - पार किसी दूर स्थित प्रकाश स्रोत को देखने पर उसके झिलमिल करते हुए दिखाई देने का कारण है:
(क) परावर्तन 
(ख)अपवर्तन
(ग) विवर्तन
(घ) वर्ण विक्षेपण 
उत्तर:
(ख)अपवर्तन

प्रश्न 8. 
पतले लैंसों में से आपतित किरण अपने मार्ग से विचलित हुये बिना सीधे उसी दिशा में निकल जाती है। मुख्य अक्ष पर ऐसे बिन्दु को कहते हैं:
(क) फोकस 
(ख) प्रकाश केन्द्र 
(ग) प्रतिबिम्ब
(घ) वक्रता केन्द्र 
उत्तर:
(ख) प्रकाश केन्द्र 

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1. 
निम्नलिखित आरेख को अपनी उत्तर - पुस्तिका में खींचकर लैंस के पार किरण पथ की पूर्ति कीजिए

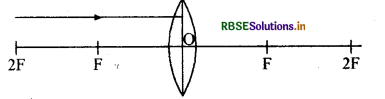
उत्तर:

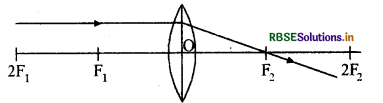
प्रश्न 2. 
फोकस दूरी को परिभाषित कीजिए। 
उत्तर:
किसी लैंस के मुख्य फोकस बिन्दु एवं प्रकाशीय केन्द्र के बीच की दूरी को फोकस दूरी कहते हैं। 

प्रश्न 3. 
एक गोलीय दर्पण की वक्रता त्रिज्या 30 सेमी. है। इसकी फोकस दूरी क्या होगी? 
उत्तर: 
∵ R = 2f  
∴ f = R =\( \frac{R}{2}=\frac{30}{2}\) सेमी 
अतः दर्पण की फोकस दूरी 15 सेमी. होगी। 

प्रश्न 4. 
'विवर्तन' किसे कहते हैं?
उत्तर:
यदि प्रकाश के पथ में रखी अपारदर्शी वस्तु अत्यंत छोटी हो तो प्रकाश सरल रेखा में चलने की बजाय इसके किनारों पर मुड़ने की प्रवृत्ति दर्शाता है - इस प्रभाव को प्रकाश का विवर्तन कहते हैं।

प्रश्न 5. 
'विवर्तन' प्रभाव की व्याख्या प्रकाश की किस प्रकृति द्वारा की जा सकती है? 
उत्तर:
विवर्तन प्रभाव की व्याख्या प्रकाश की तरंग प्रकृति के आधार पर की जा सकती है। 

प्रश्न 6. 
प्रकाश का आधुनिक क्वांटम सिद्धान्त क्या है?
उत्तर:
प्रकाश का आधुनिक क्वांटम सिद्धान्त प्रकाश के कण संबंधी गुणों तथा तरंग प्रकृति के बीच सामंजस्य स्थापित करता है।

प्रश्न 7. 
एक शेविंग दर्पण में हमें अपना प्रतिबिंब कैसा दिखता है? 
उत्तर:
आभासी, बड़ा एवं सीधा प्रतिबिंब। 

प्रश्न 8. 
नीचे दिए गए आरेख को अपनी उत्तर - पुस्तिका में खींचकर किरण पथ की पूर्ति कीजिए - 

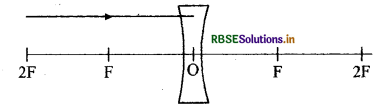
उत्तर:

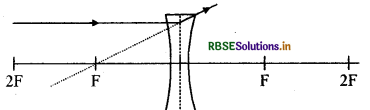
प्रश्न 9. 
यदि प्रकाश की किरण काँच की पट्टिका पर लम्बवत् आपतित होती है तो अपवर्तन कोण का मान कितना होगा? 
उत्तर:
अपवर्तन कोण का मान शून्य होगा। 

प्रश्न 10. 
सरल सूक्ष्मदर्शी में कैसा लैंस प्रयुक्त करते हैं ? 
उत्तर:
इसमें कम फोकस दूरी का एक उत्तल लैंस होता है।

प्रश्न 11. 
प्रकाश की किरणों को फैलाने वाले लैंस का नाम बताओ। 
उत्तर:
अवतल लैंस। 

प्रश्न 12. 
लैंस की फोकस दूरी किन कारकों पर निर्भर करती है ? 
उत्तर:
किसी लैंस की फोकस दूरी निम्नलिखित कारकों पर निर्भर करती है:

1. लैंस के पदार्थ के अपवर्तनांक पर।  
2. लैंस के दोनों वक्र पृष्ठों की वक्रता त्रिज्याओं R₁ व R₂ पर।
3. प्रकाश के वर्ण (तरंगदैर्घ्य) पर। 

प्रश्न 13. 
किसी अवतल दर्पण की वक्रता त्रिज्या 10 cm है तब उस अवतल दर्पण की फोकस दूरी कितनी होगी? 
उत्तर: 
∵ f = \( \frac{R}{2} \)
∵ f = \(\frac{-10}{2} \) = -5 cm  
अतः फोकस दूरी 5 cm होगी। 

प्रश्न 14. 
'अवतल दर्पण' क्या होता है?
उत्तर:
वह गोलीय दर्पण जिसका परावर्तक पृष्ठ अन्दर की ओर अर्थात् गोले के केन्द्र की ओर वक्रित है अवतल दर्पण कहलाता है।

प्रश्न 15. 
'दर्पण का ध्रुव' किसे कहते हैं? 
उत्तर:
गोलीय दर्पण के परावर्तक पृष्ठ के केन्द्र को 'दर्पण का ध्रुव' कहते हैं। 

प्रश्न 16. 
गोलीय दर्पण की वक्रता त्रिज्या (R) तथा फोकस दूरी (f) के बीच क्या संबंध है? 
उत्तर:
छोटे द्वारक के गोलीय दर्पणों के लिए वक्रता त्रिज्या फोकस दूरी से दोगुनी होती है अर्थात् R = 2f 

प्रश्न 17. 
आगरा किले की एक दीवार में किस प्रकार का दर्पण ताजमहल की ओर लगा हुआ है? 
उत्तर:
उत्तल दर्पण 

प्रश्न 18. 
बिंब दूरी तथा प्रतिबिंब दूरी से क्या तात्पर्य है?
उत्तर:
ध्रुव से बिंब की दूरी को बिंब दूरी (u) कहते हैं जबकि ध्रुव से प्रतिबिंब की दूरी को प्रतिबिंब दूरी (v) कहते हैं।

प्रश्न 19. 
'लेंस' किसे कहते है? 
उत्तर:
दो पृष्ठों से घिरा हुआ कोई पारदर्शी माध्यम, जिसका एक या दोनों पृष्ठ गोलीय हों, लैंस कहलाता है। 

प्रश्न 20. 
उस दर्पण का नाम लिखिये जो वस्तु का बड़ा एवं कल्पित प्रतिबिम्ब बनाता है। 
उत्तर:
अवतल दर्पण। 

प्रश्न 21. 
यदि कोई वस्तु उत्तल दर्पण के ध्रुव तथा अनन्त के मध्य रखी जाये तब उसका प्रतिबिम्ब कहाँ बनेगा? 
उत्तर:
दर्पण के फोकस तथा ध्रुव के मध्य तथा दर्पण के पीछे। 

प्रश्न 22. 
उस दर्पण का क्या नाम है जिसका प्रयोग दन्त चिकित्सक अपने रोगी के दाँत देखने के लिए करता है? 
उत्तर:
अवतल दर्पण।

प्रश्न 23. 
अवतल दर्पण के मुख्य अक्ष पर कोई वस्तु किस स्थान पर रखी जाये जिससे इस वस्तु का वास्तविक प्रतिबिम्ब प्राप्त हो सके, जिसकी माप वस्तु की लम्बाई के बराबर है?
उत्तर:
वस्तु को अवतल दर्पण के वक्रता केन्द्र पर रखना चाहिये।

प्रश्न 24. 
दर्पण के रैखिक आवर्धन को परिभाषित कीजिये।
उत्तर:
दर्पण के रैखिक आवर्धन को प्रतिबिम्ब की ऊँचाई तथा वस्तु की ऊँचाई के अनुपात रूप में परिभाषित किया जाता है।

प्रश्न 25. 
किसी लैंस की दोनों फोकस दूरियाँ कब बराबर होती हैं? 
उत्तर:
लैंस के दोनों ओर एकसमान माध्यम तथा दोनों वक्रता त्रिज्यायें समान होने पर लैंस की दोनों फोकस दूरियाँ समान होंगी।

प्रश्न 26. 
अपवर्तन का प्रथम नियम लिखो। 
उत्तर:
आपतित किरण, अपवर्तित किरण एवं अभिलम्ब तीनों एक ही तल में होते हैं। यह अपवर्तन का प्रथम नियम है। 

प्रश्न 27. 
प्रकाश की किरणों को केन्द्रित करने के लिए कौनसा लैंस प्रयुक्त किया जाता है? 
उत्तर:
अभिसारी या उत्तल लैंस। 

प्रश्न 28. 
प्रकाश की किरण का सघन से विरल माध्यम में प्रवेश करने पर उसके वेग पर क्या प्रभाव पड़ेगा? 
उत्तर:
प्रकाश किरण का वेग बढ़ जाता है।

प्रश्न 29. 
जब प्रकाश की किरण विरल माध्यम से सघन माध्यम में जाती है तब आपतन और अपवर्तन कोण में से किस कोण का मान अधिक होता है?
उत्तर:
आपतन कोण का। 

प्रश्न 30. 
सघन व विरल माध्यम में क्या अन्तर है? 
उत्तर:
सघन माध्यम में प्रकाश वेग, निर्वात की अपेक्षा कम जबकि विरल माध्यम में, सघन की अपेक्षा अधिक होता है। 

प्रश्न 31. 
अपवर्तन किसे कहते हैं?
उत्तर:
प्रकाश की किरण का एक माध्यम से दूसरे माध्यम में प्रवेश करते समय पृथक्कारी तल पर इसकी दिशा में विचलन की क्रिया को अपवर्तन कहते हैं।

प्रश्न 32. 
एक उत्तल लैंस किसी वस्तु का वास्तविक तथा बहुत बड़ा प्रतिबिम्ब बनाता है। मुख्य अक्ष पर वस्तु की क्या स्थिति होनी चाहिये?
उत्तर:
वस्तु लैंस के फोकस पर स्थित होनी चाहिये। 

प्रश्न 33. 
'उत्तल दर्पण' किसे कहते हैं? 
उत्तर:
वह गोलीय दर्पण जिसका परावर्तक पृष्ठ बाहर की ओर वक्रित होता है, उत्तल दर्पण कहलाता है। 

प्रश्न 34. 
दर्पण तथा लेंस की फोकस दूरी (f) में अन्तर कीजिए। 
उत्तर:

दर्पण की फोकस दूरी	लेंस की फोकस दूरी
गोलीय दर्पण के ध्रुव तथा मुख्य फोकस के बीच दूरी	लेंस के प्रकाशिक केन्द्र से मुख्य फोकस की दूरी

प्रश्न 35. 
आवर्धन के मान में ऋणात्मक चिह्न से क्या ज्ञात होता है? 
उत्तर:
आवर्धन के मान में ऋणात्मक चिह्न से ज्ञात होता है कि प्रतिबिंब वास्तविक है। 

प्रश्न 36. 
प्रकाश का अपवर्तन क्यों होता है?
उत्तर:
अपवर्तन प्रकाश के एक पारदर्शी माध्यम से दूसरे में प्रवेश करने पर प्रकाश की चाल में परिवर्तन के कारण होता है। 

प्रश्न 37. 
किसी लेंस की प्रकाश किरणों को अभिसरित अथवा अपसरित करने की क्षमता किस पर निर्भर करती है?
उत्तर:
किसी लेंस की प्रकाश किरणों को अभिसरित अथवा अपसरित करने की क्षमता उसकी फोकस दूरी पर निर्भर करती है।

प्रश्न 38. 
लैंस के प्रकाशिक केन्द्र का क्या अभिप्राय है?
उत्तर:
लैंस में स्थित वह बिन्दु जिससे होकर जाने वाली प्रकाश की किरण, बिना अपने मार्ग से विचलित हुये, लैंस से बाहर निकल जाती है।

प्रश्न 39. 
एक उत्तल लैंस के द्वारा कल्पित एवं बड़ा प्रतिबिम्ब बनता है। मुख्य अक्ष पर वस्तु की स्थिति क्या होनी चाहिये?
उत्तर:
वस्तु लैंस के फोकस एवं प्रकाशिक केन्द्र के मध्य स्थित होनी चाहिये।

प्रश्न 40. 
लैंस के मुख्य अक्ष के समानान्तर किरण पुंज लैंस में से अपवर्तित होने के पश्चात् मुख्य अक्ष पर स्थित एक बिन्दु पर केन्द्रित हो जाता है, उस बिन्दु को कहते हैं।
उत्तर:
फोकस।

प्रश्न 41. 
एक से अधिक लैंसों का प्रयोग किस - किस में किया जाता है?
उत्तर:
एक से अधिक लैंसों का प्रयोग कैमरे की रचना, दूरदर्शी तथा सूक्ष्मदर्शी के वस्तु लैंस में किया जाता है। 

लघूत्तरात्मक प्रश्न

प्रश्न 1. 
लैंस की क्षमता को परिभाषित कीजिये। इसकी इकाई और सूत्र को लिखिये।
उत्त:
लैंस की क्षमता - किसी लैंस द्वारा प्रकाश किरणों को अभिसरण या अपसरण करने की मात्रा (Degree) को उसकी क्षमता के रूप में व्यक्त किया जाता है। इसे P से व्यक्त करते हैं। किसी f फोकस दूरी के लैंस की क्षमता,
P = \(\frac{1}{f}\)
लैंस की क्षमता का SI मात्रक ‘डाइऑप्टर' (Dioptre) है। इसे D से व्यक्त करते हैं। यदि को मीटर में व्यक्त करें तो क्षमता को डाइऑप्टर में व्यक्त किया जाता है। इस प्रकार 1 डाइऑप्टर उस लैंस की क्षमता है, जिसकी फोकस दूरी 1 मीटर हो। अतः
ID = 1m^-1 
उत्तल लैंस की क्षमता धनात्मक तथा अवतल लैंस की क्षमता ऋणात्मक होती है। 

प्रश्न 2. 
प्रकाश की प्रकृति को स्पष्ट कीजिए।
उत्तर:
अपने चारों ओर कुछ सामान्य प्रकाशिक परिघटनाओं को देखकर निष्कर्ष निकाल सकते हैं कि प्रकाश सरल रेखाओं में गमन करता प्रतीत होता है। परन्तु प्रकाश के पथ में रखी आपारदर्शी वस्तु अत्यंत छोटी हो तो प्रकाश सरल रेखा में चलने की बजाय इसके किनारों पर मुड़ने की प्रवृत्ति दर्शाता है। इस प्रभाव को प्रकाश का विवर्तन कहते हैं। तब वह प्रकाशिकी जिसमें सरलरेखीय व्यवहार के आधार पर किरणों का उपयोग करते हैं असफल होने लगती है।

विवर्तन जैसी परिघटनाओं की व्याख्या करने के लिए प्रकाश को तरंग के रूप में माना जाता है। लेकिन प्रकाश की द्रव्य के साथ अन्योन्य क्रिया के विवेचन में प्रकाश का तरंग सिद्धान्त अपर्याप्त है तथा प्रकाश प्रायः कणों के प्रवाह की भाँति व्यवहार करता है। प्रकाश के आधुनिक क्वांटम सिद्धान्त में प्रकाश को न तो 'तरंग' माना गया न ही 'कण' । यह सिद्धान्त प्रकाश के कण संबंधी गुणों तथा तरंग प्रकृति के बीच सामंजस्य स्थापित करता है।

प्रश्न 3. 
(A) प्रकाश के परावर्तन से क्या तात्पर्य है? 
(B) प्रकाश के परावर्तन के नियम चित्र की सहायता से लिखिए।
उत्तर:
(A) प्रकाश का परावर्तन - जब कोई प्रकाश की किरण एक माध्यम से चलकर दूसरे माध्यम की सतह से टकराकर वापस उसी माध्यम में लौट जाती है, तो इस घटना को प्रकाश का परावर्तन कहते हैं।

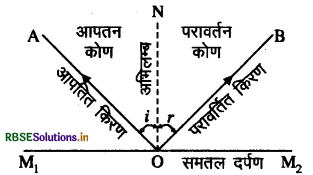
(B) प्रकाश के परावर्तन के नियम निम्न प्रकार से हैं:

1. आपतित किरण, परावर्तित किरण तथा दर्पण के आपतन बिन्दु पर अभिलम्ब एक ही तल में होते हैं। 
2. आपतन कोण ∠i, परावर्तन कोण ∠r के बराबर होता है। 
3. परावर्तित किरण की आवृत्ति एवं चाल अपरिवर्तित रहती है।

प्रश्न 4. 
समतल दर्पण द्वारा बने प्रतिबिंब की क्या विशेषताएँ होती हैं?
उत्तर:
समतल दर्पण द्वारा बना प्रतिबिंब सदैव आभासी तथा सीधा होता है। प्रतिबिंब का साइज बिंब (वस्तु) के साइज के बराबर होता है। प्रतिबिंब दर्पण के पीछे उतनी ही दूरी पर बनता है, जितनी दूरी पर दर्पण के सामने बिंब रखा होता है। इसके अतिरिक्त प्रतिबिंब पार्श्व परिवर्तित होता है।

प्रश्न 5. 
(A) किसी एक माध्यम से दूसरे माध्यम में जाने पर प्रकाश की किरण क्यों मुड़ जाती है? 
(B) एक लैंस की शक्ति - 4.0D है। इस लैंस की प्रकृति क्या होगी? 
उत्तर:
(A) एक माध्यम से दूसरे माध्यम में जाने पर प्रकाश की किरण अपवर्तन के कारण मुड़ जाती है।
(B) लैंस की क्षमता/शक्ति ऋणात्मक है। अतः इस लैंस की फोकस दूरी भी ऋणात्मक होगी, इस कारण लैंस की प्रकृति अवतल होगी।

प्रश्न 6. 
कोई 4.00 सेमी. आकार का बिम्ब किसी 15.0 सेमी. फोकस दूरी के अवतल दर्पण से 30 सेमी. की दूरी पर रखा है। दर्पण से कितनी दूरी पर किसी पर्दे को रखा जाए कि स्पष्ट प्रतिबिम्ब प्राप्त हो? प्रतिबिम्ब की प्रकृति तथा आकार ज्ञात कीजिए। 
उत्तर:
बिम्ब का आकार h = 4 सेमी.
फोकस दूरी f = -15 सेमी. 
दर्पण से बिम्ब की दूरी u = - 30 सेमी. 
दर्पण से प्रतिबिम्ब की दूरी v = ? 
दर्पण का सूत्र: 
\(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}\)
\(\frac{1}{v}=-\frac{1}{15}-\frac{1}{-30} \Rightarrow \frac{-2+1}{30} \Rightarrow \frac{1}{-30} \)  सेमी
v = – 30 सेमी. अतः पर्दे को दर्पण से 30 सेमी. दूर रखना चाहिए। 
दर्पण में उत्पन्न आवर्धन
m=\(\frac{h^{\prime}}{h}=\frac{-v}{u}\)
\(h^{\prime}=-\left(\frac{v}{u}\right) \times h\)
\(h^{\prime}=-\left(\frac{-30}{-30}\right) \times 4\)
\(=-\frac{120}{30} \Rightarrow-4 \) सेमी. 
अतः प्रतिबिम्ब की ऊँचाई h' = - 4 सेमी.
अतः प्रतिबिम्ब वास्तविक, उल्टा तथा आवर्धित बनेगा। 

प्रश्न 7. 
दर्पण व लेंस में अन्तर कीजिए।
उत्तर:
दर्पण व लेंस के अन्तर: 

दर्पण	लेंस
1. किसी काँच की पट्टिका के किसी एक ओर परावर्तक पदार्थ की पॉलिश करने पर दर्पण बनता है।	यह पूर्ण रूप से पारदर्शी माध्यम होता है जो दो पृष्ठों से घिरा होता है।
2. यह दो प्रकार के होते हैं- समतल दर्पण अवतल लेंस	यह भी दो प्रकार के होते हैं- उत्तल लेंस गोलीय दर्पण
3. इसमें एक ही गोलीय पृष्ठ पाया जाता है।	इसमें दो गोलीय पृष्ठ पाये जाते हैं।
4. उपयोग - टॉर्च, सर्चलाइट वाहनों के अग्रदीपों में, शेविंग दर्पणों में, सौर भट्टियों में, वाहनों के पश्च - दृश्य दर्पणों में।	उपयोग - कैमरा, सूक्ष्मदर्शी एवं दूरदर्शी में।

प्रश्न 8. 
15 सेमी. फोकस दूरी वाले अवतल दर्पण से 20 सेमी. की दूरी पर एक वस्तु रखी है। प्रतिबिम्ब की स्थिति एवं प्रकार बताइए। 
उत्तर:
वस्तु की दर्पण से दूरी u = - 20 सेमी. 
दर्पण की फोकस दूरी f = - 15 सेमी. (: दर्पण अवतल है) 
प्रतिबिम्ब की दूरी v = ? 
दर्पण सूत्र से -
\(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}\)

मान रखने पर-
\(\frac{1}{v}=\left(\frac{1}{-15}\right)-\left(\frac{1}{-20}\right)\)
=\(-\frac{1}{15}+\frac{1}{20} \Rightarrow \frac{-4+3}{60} \Rightarrow-\frac{1}{60}\)
∴ v = - 60 सेमी. 
∵ ऋणात्मक है, अतः प्रतिबिम्ब दर्पण के सामने 60 सेमी. की दूरी पर वास्तविक तथा उल्टा बनेगा।

प्रश्न 9. 
रेखाचित्र की सहायता से अवतल दर्पण के सम्मुख निम्नलिखित स्थितियों में रखी वस्तु के प्रतिबिम्ब की स्थिति तथा प्रकार बताइए
(क) जब वस्तु F तथा C के बीच हो। 
(ख) जब वस्तु F तथा P के बीच हो। 
उत्तर:
(क) जब वस्तु F तथा C के बीच हो -

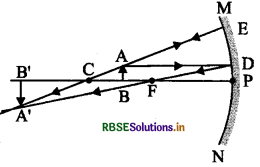
रेखाचित्र से स्पष्ट है कि वस्तु का प्रतिबिम्ब C तथा अनन्त (∝) के बीच वास्तविक, उल्टा तथा बड़ा बनेगा। 

(ख) जब वस्तु F तथा P के बीच स्थित हो -

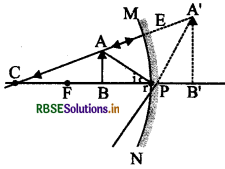
रेखाचित्र से स्पष्ट है कि वस्तु का प्रतिबिम्ब दर्पण के पीछे आभासी, सीधा एवं बड़ा बनेगा।

प्रश्न 10. 
प्रकाश हवा से जल में प्रवेश करता है, जिसका अपवर्तनांक 1.33 है। जल में प्रकाश की चाल ज्ञात कीजिए। यदि हवा में प्रकाश की चाल 3 x 108 मी./से. है। 
उत्तर:
दिया है - 
प्रकाश का हवा में वेग c = 3 x 10⁸ मी./से.  
जल का अपवर्तनांक n = 1.33 
जल में प्रकाश का वेग v = ?
अपवर्तनांक n =\( \frac{\mathcal{C}}{v}\)
v = \(\frac{c}{n}\)
मान रखने पर -    
v = \(\frac{3 \times 10^{8}}{1.33}\) = 2.25x10⁸ 
अतः जल में प्रकाश का वेग 2.25 x 10⁸ मी./से. होगा।

प्रश्न 11. 
नीचे दिए गए आरेख को उसके आगे दी गई जगह में खींचकर उपयुक्त किरणों की सहायता से बिम्ब AB का प्रतिबिम्ब बनना दिखाइए।

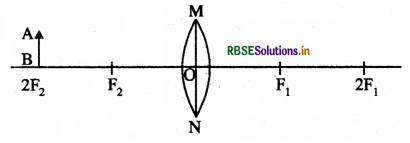
उत्तर:

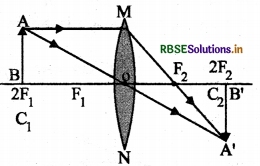
प्रश्न 12. 
कोई वस्तु किसी अवतल दर्पण के वक्रता केन्द्र पर रखी गई है। बनने वाले प्रतिबिम्ब का किरण आरेख खींचिए।
उत्तर:
अवतल दर्पण के वक्रता केन्द्र से गुजरने वाली किरण परावर्तन के बाद उसी पथ के अनुदिश वापस परावर्तित हो जाती है।

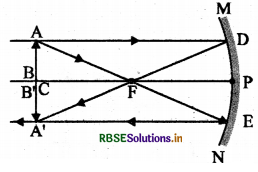
प्रश्न 13. 
एक उत्तल लैंस की फोकस दूरी 20 सेमी. है। लैंस की क्षमता कितनी होगी? 
उत्तर:
दिया गया है - 
उत्तल लैंस की फोकस दूरी f = 20 सेमी.
\(\frac{20}{100} = \frac{1}{5}\) मी. 
लैंस की क्षमता P = \(\frac{1}{f}\)
∴ P = \(\frac{1}{1 / 5}\) मी.
P = +5D

प्रश्न 14. 
लैंस सूत्र क्या होता है? समझाइए।
उत्तर:
गोलीय लैंसों के लिए बिंब दूरी (u), प्रतिबिंब दूरी (v) तथा फोकस दूरी (f) के बीच संबंध को एक सूत्र द्वारा व्यक्त किया जा सकता है, जिसे लेंस सूत्र कहते हैं।
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
उपरोक्त लेंस सूत्र व्यापक है तथा किसी भी गोलीय लेंस के लिए, सभी स्थितियों में मान्य है। 

प्रश्न 15. 
निम्न की परिभाषायें लिखिये:
(i) समतल दर्पण 
(ii) गोलीय दर्पण।
उत्तर:
(i) समतल दर्पण: जब समतल काँच की प्लेट के किसी एक पृष्ठ पर परावर्तक पॉलिश कर देते हैं तो उसे समतल दर्पण कहते हैं।
(ii) गोलीय दर्पण: ऐसे दर्पण जिनका परावर्तक पृष्ठ गोलीय होता है, गोलीय दर्पण कहलाते हैं। ये दो प्रकार के होते हैं- 
(क) उत्तल दर्पण 
(ख) अवतल दर्पण।

(क) उत्तल दर्पण: वह गोलीय दर्पण, जिसका परावर्तक पृष्ठ बाहर की ओर वक्रित होता है, उत्तल दर्पण कहलाता है।

(ख) अवतल दर्पण: वह गोलीय दर्पण, जिसका परावर्तक पृष्ठ अंदर की ओर अर्थात् गोले के केन्द्र की ओर वक्रित होता है, अवतल दर्पण कहलाता है।

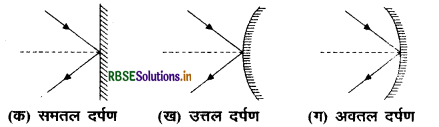
प्रश्न 16. 
गोलीय दर्पण द्वारा परावर्तन के नियमों का उल्लेख कीजिए। 
उत्तर:
गोलीय दर्पण द्वारा परावर्तन के नियम: 

1. मुख्य अक्ष के समान्तर कोई भी प्रकाश किरण गोलीय दर्पण पर आपतित होती है तो परावर्तन के पश्चात् मुख्य फोकस से जाती है या जाती हुई प्रतीत होती है।
2. गोलीय दर्पण पर कोई किरण वक्रता केन्द्र से गुजरती हुई आपतित होती है तो परावर्तन के बाद अपने ही मार्ग में लौट आती है।
3. गोलीय दर्पण में फोकस में से होती हुई कोई किरण आपतित होती है तो परावर्तन के पश्चात् वह मुख्य अक्ष के समान्तर हो जाती है।
4. इन नियमों के आधार पर किरणें खींच कर दर्पण द्वारा किसी वस्तु का प्रतिबिम्ब बनाया जाता है | 

प्रश्न 17. 
अभिसारी लेंस व अपसारी लेंस में अन्तर कीजिए।
उत्तर: 

अभिसारी लेंस	अपसारी लेंस
1. यह प्रकाश किरणों को अभिसरित करता है।	यह प्रकाश किरणों को अपसरित करता है।
2. इसमें बाहर की ओर उभरे दो गोलीय पृष्ठ हो सकते हैं।	इसमें अंदर की ओर वक्रित दो गोलीय पृष्ठ हो सकते हैं।
3. यह किनारों की अपेक्षा बीच से मोटा होता है।	यह बीच की अपेक्षा किनारों से मोटा होता है।
4. दूर दृष्टि दोष को दूर करने में प्रयुक्त ।	निकष्ट दृष्टि दोष को दूर करने में प्रयुक्त।

प्रश्न 18.
वास्तविक तथा कल्पित (आभासी) प्रतिबिम्ब में अन्तर लिखिये। 
उत्तर:

वास्तविक प्रतिबिम्ब	कल्पित (आभासी) प्रतिबिम्ब
1. प्रकाश की किरणें परावर्तन के बाद जब किसी बिन्दु पर मिलती हैं तब वास्तविक प्रतिबिम्ब बनता है।	प्रकाश की किरणें यदि परावर्तन के बाद किसी बिन्दु पर नहीं मिलतीं परन्तु उस बिन्दु पर मिलती हुई दिखायी देती हैं तब कल्पित प्रतिबिम्ब बनता है।
2. वास्तविक प्रतिबिम्ब को पर्दे पर उतारा जा सकता है।	कल्पित प्रतिबिम्ब को पर्दे पर नहीं उतारा जा सकता।
3. वास्तविक प्रतिबिम्ब दर्पण के सम्मुख बनते हैं।	कल्पित प्रतिबिम्ब दर्पण के पीछे बनते हैं।
4. वास्तविक प्रतिबिम्ब सदैव उल्टे बनते हैं।	कल्पित प्रतिबिम्ब सदैव सीधे बनते हैं।

प्रश्न 19. 
गोलीय दर्पणों से संबंधित निम्न को परिभाषित कीजिये - (कोई तीन) 
(i) ध्रुव 
(ii) मुख्य अक्ष 
(iii) मुख्य अक्ष 
(iv) मुख्य फोकस 
(v) फोकस दूरी। 
उत्तर:
(i) ध्रुव: गोलीय दर्पण के परावर्तक तल का मध्य बिन्दु गोलीय दर्पण का ध्रुव (Pole) कहलाता है। 

(ii) मुख्य अक्ष: गोलीय दर्पण के वक्रता केन्द्र C तथा ध्रुव P को मिलाने वाली रेखा, मुख्य अक्ष कहलाती है।

(iii) मुख्य फोकस: मुख्य अक्ष पर स्थित वह बिन्दु जहाँ पर मुख्य अक्ष के समानान्तर चलने वाला किरण पुंज दर्पण से परावर्तन के उपरान्त मिलता है या मिलता हुआ प्रतीत होता है, उसे मुख्य फोकस कहते हैं। इसे F के द्वारा निरूपित किया जाता है।

(iv) फोकस दूरी: किसी गोलीय दर्पण के ध्रुव P तथा फोकस F के बीच की दूरी दर्पण की फोकस दूरी कहलाती है। इसे f से निरूपित करते हैं। 

प्रश्न 20. 
किसी गोलीय दर्पण की वक्रता केन्द्र और वक्रता त्रिज्या तथा द्वारक को परिभाषित कीजिये।
उत्तर:
वक्रता केन्द्र: गोलीय दर्पण का परावर्तक पृष्ठ एक गोले का भाग है, इस गोले का केन्द्र गोलीय दर्पण का वक्रता केन्द्र कहलाता है। इसको C से निरूपित किया जाता है। वक्रता केन्द्र दर्पण का भाग नहीं होता है। यह तो परावर्तक पृष्ठ के बाहर स्थित होता है । अवतल दर्पण का वक्रता केन्द्र परावर्तक पृष्ठ के सामने स्थित होता है जबकि उत्तल दर्पण की स्थिति में यह परावर्तक पृष्ठ के पीछे स्थित होता है। 

वक्रता त्रिज्या: गोलीय दर्पण का परावर्तक पृष्ठ जिस गोले का भाग है उसकी त्रिज्या दर्पण की वक्रता त्रिज्या कहलाती है। इसे अक्षर R से प्रदर्शित करते हैं।

द्वारक: गोलीय दर्पण का परावर्तक पृष्ठ अधिकांशतः गोलीय ही होता है। इस पृष्ठ की एक वृत्ताकार सीमा रेखा होती है। गोलीय दर्पण के परावर्तक पृष्ठ की इस वृत्ताकार सीमा रेखा का व्यास दर्पण का द्वारक कहलाता है।

प्रश्न 21. 
किसी उत्तल लेंस द्वारा सूर्य के प्रकाश को कागज की शीट पर फोकसित करने पर कागज जलने क्यों लगता है?
उत्तर:
सूर्य से आने वाली प्रकाश की किरणें समानान्तर होती हैं। उत्तल लेंस द्वारा यह किरणें एक तीक्ष्ण चमकदार बिंदु के रूप में कागज पर अभिकेन्द्रित कर दी जाती हैं। वास्तव में, कागज की शीट पर यह चमकदार बिंदु सूर्य का प्रतिबिंब है। एक बिंदु पर सूर्य के प्रकाश का संकेद्रण ऊष्मा उत्पन्न करता है। इसके कारण कागज जलने लगता है। 

प्रश्न 22. 
किसी अवतल दर्पण द्वारा वस्तु की विभिन्न स्थितियों के लिये बने हुये प्रतिबिम्ब की जानकारी दीजिये।
उत्तर:
किसी अवतल दर्पण द्वारा बिम्ब की विभिन्न स्थितियों के लिए बने प्रतिबिम्ब:  

वस्तु की स्थिति	प्रतिबिम्ब की स्थिति	प्रतिबिम्ब का आकार	प्रतिबिम्ब की प्रकृति
1. अनंत पर स्थित हो	फोकस F पर	अत्यधिक छोटा, बिंदु साइज	वास्तविक एवं उल्टा
2. C से दूर हो	F तथा C के बीच	छोटा	वास्तविक एवं उल्टा
3. C पर स्थित हो	C पर	समान साइज	वास्तविक एवं उल्टा
4. C तथा F के बीच स्थित हो	C से परे	विवर्धित (बड़ा)	वास्तविक एवं उल्टा
5. F पर स्थित हो	अनंत पर	अत्यधिक विवर्धित	वास्तविक एवं उल्टा
6. P तथा F के बीच दर्पण के पीछे स्थित हो	दर्पण के पीछे	विवर्धित (बड़ा)	आभासी तथा सीधा

प्रश्न 23. 
किसी अवतल दर्पण द्वारा प्रतिबिम्ब का किरण आरेख खींचिये जबकि वस्तु की स्थिति निम्न पर स्थित हो:
(i) अनन्त पर 
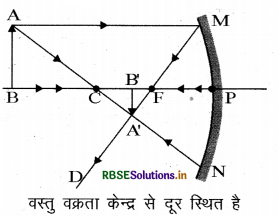
(ii) वक्रता केन्द्र से दूर। 
उत्तर:
(i) अनन्त पर:

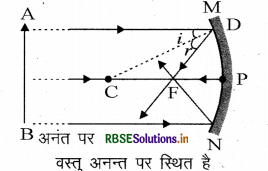
(ii) वक्रता केन्द्र से दूर:

प्रश्न 24. 
गोलीय दर्पणों तथा गोलीय लेंसों के लिए चिह्न परिपाटी में क्या अंतर है?
उत्तर: 

गोलीय दर्पण चिह्न परिपाटी	गोलीय लेंस चिह्न परिपाटी
1. इस परिपाटी में दर्पण के ध्रुव (P) को मूल बिन्दु मानते हैं।	इस परिपाटी में लेंस के प्रकाशिक केन्द्र (O) को मूल बिन्दु मानते हैं।
2. दर्पणों में सभी दरियाँ उनके ध्रुवों से मापी जाती हैं।	लेंसों में सभी माप उनके प्रकाशिक केन्द्रों से लिए जाते हैं।
3. मूल बिन्दु के दाईं ओर मापी गई सभी दूरियाँ धनात्मक तथा बाईं ओर मापी गई दूरियाँ ऋणात्मक मानी जाती हैं।	इस परिपाटी के अनुसार उत्तल लेंस की फोकस दूरी धनात्मक जबकि अवतल लेंस की फोकस दूरी ऋणात्मक होती है।

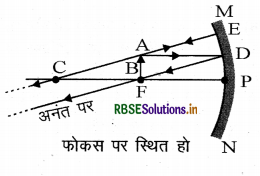
प्रश्न 25. 
किसी अवतल दर्पण द्वारा प्रतिबिम्ब का किरण आरेख खींचिये जबकि वस्तु फोकस F पर स्थित हो। 
उत्तर:

प्रश्न 26. 
अवतल दर्पणों के उपयोग लिखिये।
उत्तर:

1. इनका उपयोग सामान्यतः टॉर्च, सर्चलाइट तथा वाहनों के अग्रदीपों (Headlights) में प्रकाश का शक्तिशाली समान्तर किरण पुंज प्राप्त करने के लिये किया जाता है।
2. दंत विशेषज्ञ इनका उपयोग मरीजों के दाँतों का बड़ा प्रतिबिम्ब देखने के लिये करते हैं। 
3. सौर भट्टियों में इनका उपयोग सूर्य के प्रकाश को केन्द्रित करने में किया जाता है। 
4. चेहरे का बड़ा प्रतिबिम्ब देखने के लिये शेविंग दर्पणों के रूप में भी इनका उपयोग करते हैं।

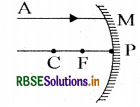
प्रश्न 27. 
प्रकाश की किरण AM गोलीय दर्पण पर पड़ती है, जैसा चित्र में दिखाया गया है। इस चित्र को दोबारा बनायें और परावर्तित किरण दिखायें। आपतन कोण और परावर्तित कोण भी चिन्हित करें।

उत्तर:
किरण AM मुख्य अक्ष के समानान्तर है, अतः यह किरण परावर्तन के पश्चात् दर्पण के फोकस बिन्दु से गुजरेगी, जैसा चित्र में दिखाया गया है।

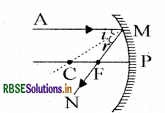
चित्र में:
(क) आपतन कोण = AMC
(ख) परावर्तन कोण = NMC

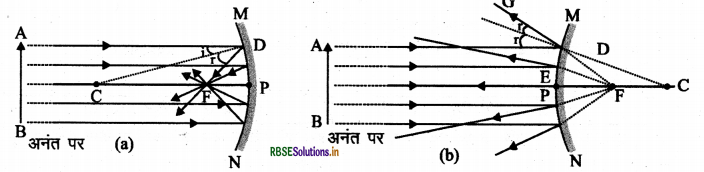
प्रश्न 28. 
समांतर प्रकाश किरणों द्वारा अवतल दर्पण एवं उत्तल दर्पण के मुख्य फोकस (F) को निर्धारित करने के लिए किरण आरेख बनाइए।
उत्तर:

प्रश्न 29. 
दर्पण सूत्र तथा आवर्धन (अथवा रैखिक आवर्धन) से आप क्या समझते हैं?
उत्तर:
1. दर्पण सूत्र:
गोलीय दर्पण में ध्रुव से वस्तु की दूरी, बिंब दूरी (u) कहलाती है। दर्पण के ध्रुव से प्रतिबिंब की दूरी, प्रतिबिंब दूरी (v) कहलाती है तथा ध्रुव से मुख्य फोकस की दूरी, फोकस दूरी (f) कहलाती है। इन तीनों राशियों के बीच एक सम्बन्ध होता है जिसे दर्पण सूत्र कहते हैं।
इस सूत्र को निम्न प्रकार से व्यक्त करते हैं:
\(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)

2. आवर्धन (अथवा रैखिक आवर्धन):
गोलीय दर्पण द्वारा उत्पन्न आवर्धन वह आपेक्षिक विस्तार है, जिससे ज्ञात होता है कि कोई प्रतिबिम्ब बिम्ब की अपेक्षा कितना गुना आवर्धित है। इसे प्रतिबिम्ब की ऊँचाई तथा बिम्ब की ऊँचाई के अनुपात के रूप में व्यक्त किया जाता है। यदि 'h बिम्ब की ऊँचाई एवं h' प्रतिबिम्ब की ऊँचाई हो तो गोलीय दर्पण द्वारा उत्पन्न आवर्धन (m) होगा:

m = \(\frac{h^{\prime}}{h}\)
आवर्धन m वस्तु की दूरी (u) तथा प्रतिबिम्ब दूरी (v) से भी संबंधित है। इसे निम्न प्रकार व्यक्त किया जाता है -
आवर्धन m = \(\frac{h^{\prime}}{h}=-\frac{v}{u}\)
रैखिक आवर्धन की कोई इकाई नहीं होती है। आवर्धन के मान में धनात्मक चिन्ह आभासी प्रतिबिम्ब को एवं ऋणात्मक चिन्ह वास्तविक प्रतिबिम्ब को बताता है। 

प्रश्न 30. 
नीचे दी गई सारणी में कुछ माध्यमों के अपवर्तनांक दिये गये हैं -

क्र.सं.	1	2	3	4	5	6
माध्यम	बर्फ	जल	मिट्टी का तेल	शीशा	रूबी	हीरा
अपवर्तनांक	1.31	1.33	1.44	1.66	1.71	2.42

उस माध्यम का नाम बताइये जिसका प्रकाशिक घनत्व अधिकतम है तथा उस माध्यम का नाम बताइये जिसका प्रकाशिक घनत्व न्यूनतम है।
उत्तर:
माध्यम का प्रकाशिक घनत्व उसके अपवर्तनांक के अनुक्रमानुपाती होता है। अतः हीरे का प्रकाशिक घनत्व अधिकतम तथा बर्फ का प्रकाशिक घनत्व न्यूनतम है। 

प्रश्न 31. 
माध्यम A, B, C तथा D के अपवर्तनांक नीचे दिये हुये हैं - 

माध्यम	अपवर्तनांक
A	1.33
B	1.44
C	1.52
D	1.65

उपरोक्त दिये गये चार माध्यमों में से किस माध्यम में प्रकाश की चाल 
(i) अधिकतम है, 
(ii) न्यूनतम है?
उत्तर:
माध्यम में प्रकाश की चाल = 
माध्यम A का अपवर्तनांक सबसे कम है। इसलिये माध्यम A में प्रकाश की चाल अधिकतम है तथा माध्यम D का अपवर्तनांक बाकी माध्यमों से ज्यादा है। इसलिए माध्यम D में प्रकाश की चाल न्यूनतम होगी।

प्रश्न 32. 
उस द्रव्य का अपवर्तनांक ज्ञात कीजिये यदि प्रकाश की किरण का आपतन कोण 45° तथा द्रव्य अपवर्तन कोण 30° है। 
उत्तर:
प्रश्नानुसार, किरण का आपतन कोण (i) = 45°
द्रव्य अपवर्तन कोण (r) = 30°
n = \( \frac{\sin i}{\sin r}\) से
n = \( \frac{\sin 45^{\circ}}{\sin 30^{\circ}}=\frac{\frac{1}{\sqrt{2}}}{\frac{1}{2}}=\frac{2}{\sqrt{2}}\)
n = \(\sqrt{2}\)  = 1.414  
अतः द्रव्य का अपवर्तनांक = 1.414 

प्रश्न 33. 
चश्मा बनाने वालों के लिए, लेंसों की फोकस दूरी के स्थान पर क्षमताओं का उपयोग करना अधिक सुविधाजनक क्यों है? समझाइए।
उत्तर:
नेक प्रकाशिक यंत्रों में कई लेंस लगे होते हैं। उन्हें प्रतिबिंब को अधिक आवर्धित तथा सुस्पष्ट बनाने के लिए संयोजित किया जाता है (जैसे नेत्र का qलेंस तथा चश्में का लेंस)। इस प्रकार संपर्क में रखे लेंसों की कुल क्षमता (P) उन लेंसों की पृथक् - पृथक् क्षमताओं (P₁, P₂, P₃+......... आदि) का बीजंगणितीय योग होती है।
 

जैसे- P = P₁ + P₂ +P₃ + ........ आँखें टैस्ट करते समय चश्मा बनाने वाला ज्ञात क्षमता वाले संशोधी लेंसों के अनेक अलग - अलग संयोजनों को संपर्क में रखकर चश्मों को टैस्ट करने वाले फ्रेम के अंदर रखता है। चश्मा बनाने वाला आवश्यक लेंस की क्षमता की गणना सरल बीजगणितीय योग के द्वारा कर लेता है। उदाहरण के लिए + 1.5 D तथा + 0.5 D क्षमता वाले दो लेंसों का संयोजन + 2.0 D क्षमता के एकल लेंस के तुल्य है। इसलिए चश्मा बनाने वालों के लिए, लेंसों की फोकस दूरी के स्थान पर क्षमताओं का उपयोग करना सुविधाजनक होता है।

प्रश्न 34. 
लैंस किसे कहते हैं? यह कितने प्रकार के होते हैं?
उत्तर:
लैंस - दो पृष्ठों से घिरा हुआ कोई पारदर्शी माध्यम, जिसका एक या दोनों पृष्ठ गोलीय हैं, लैंस कहलाता है। इसका अर्थ यह है कि लैंस का कम - से - कम एक पृष्ठ गोलीय होता है, ऐसे लैंसों में दूसरा पृष्ठ समतल हो सकता है।
लैंसों के प्रकार - लैंस निम्न दो प्रकार के होते हैं: 

1. उत्तल लैंस अथवा अभिसारी लैंस: वह लैंस जिसके दोनों तल गोलीय तल हों अथवा एक तल समतल तथा दूसरा तल गोलीय हो तथा जो किनारों पर पतला तथा मध्य से मोटा हो, उसे उत्तल लैंस कहते हैं। उत्तल लैंस अवर्धन लैंस के रूप में कार्य करता है।

2. अवतल लैंस अथवा अपसारी लैंस: वह लैंस जिसके दो पृष्ठ गोलीय हों अथवा एक पृष्ठ गोलीय तथा दूसरा पृष्ठ समतल हो तथा जो किनारे से मोटा तथा मध्य में पतला हो उसे अवतल लैंस कहते हैं। नीचे दिये गये चित्रों में उत्तल लैंस प्रकाश किरणों को अभिसरित और अवतल लैंस प्रकाश किरणों को अपसरित करता है।

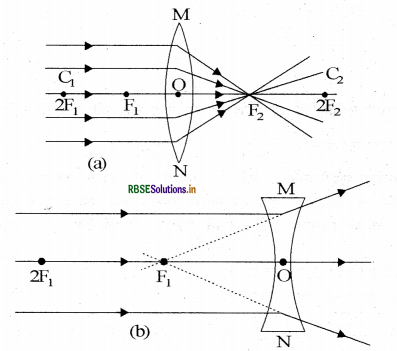
प्रश्न 35. 
लैंस से संबंधित निम्न को परिभाषित कीजिये:
(i) लैंस का वक्रता केन्द्र 
(ii) वक्रता त्रिज्या 
(iii) मुख्य अक्ष 
(iv) मुख्य फोकस 
(v) फोकस दूरी।
उत्तर:
(i) लैंस का वक्रता केन्द्र:  किसी लैंस में चाहे वह उत्तल हो अथवा अवतल, दो गोलीय पृष्ठ होते हैं। इनमें से प्रत्येक पृष्ठ एक गोले का भाग होता है। इन गोलों के केन्द्र लैंस के वक्रता केन्द्र कहलाते हैं। इसे प्रायः 'C' से दर्शाते हैं। चूँकि लैंस के दो वक्रता केन्द्र होते हैं, इसलिए इन्हें C₁ व C₂ द्वारा निरूपित किया जाता है।

(ii) वक्रता त्रिज्या: लैंस के वक्र पृष्ठों की त्रिज्याओं को लैंस की वक्रता त्रिज्या कहते हैं । जिस पृष्ठ से प्रकाश लैंस के भीतर प्रवेश करता है उसे प्रथम पृष्ठ एवं जिस पृष्ठ से वह लैंस के बाहर निकलता है, उसे द्वितीय पृष्ठ कहते हैं।

(iii) मुख्य अक्ष: किसी लैंस के दोनों वक्रता केन्द्रों C₁ एवं C₂ को मिलाने वाली काल्पनिक सीधी रेखा को लैंस की मुख्य अक्ष कहते हैं।

(iv) मुख्य फोकस: मुख्य अक्ष के समान्तर प्रकाश की किरणें लैंस पर आपतित होती हैं तो अपवर्तन के पश्चात् जिस बिन्दु पर जाकर मिलती हैं या मिलती हुई प्रतीत होती हैं, उसे मुख्य फोकस कहते हैं।मुख्य फोकस F लैंस के दोनों ओर मुख्य अक्ष पर होता है।

(v) फोकस दूरी: प्रकाश केन्द्र व मुख्य फोकस बिन्दु के मध्य की दूरी को फोकस दूरी कहते हैं। इसे f से व्यक्त करते हैं।

प्रश्न 36. 
एक सूक्ष्मदर्शी में + 0.5 D, + 1.0 D, + 2.0 D तथा + 2.5 D क्षमता के चार लैंसों का संयोजन किया गया है। सूक्ष्मदर्शी की संयुक्त क्षमता ज्ञा 
उत्तर:
किसी प्रकाशिक यंत्र में संपर्क में रखे लेंसों की कुल क्षमता (P) उन लेंसों की पृथक् - पृथक् क्षमताओं (P₁, P₂ + .......) का बीजगणितीय योग होती है: 
P = P₁  +  P₂ + P₃ + ......... 
अतः यहाँ दिया हुआ है:
P₁ = + 0.5D 
P₂ = + 1.0 D 
P₃ = + 2.0 D
P₄ = + 2.5D 
अतः सूक्ष्मदर्शी की संयुक्त क्षमता सूत्र से -
P = (+ 0.5) + (+1.0) + (+2.0) + (+2.5)
P = + 6D 

प्रश्न 37. 
वस्तु की निम्न स्थितियों के लिये अवतल लैंस द्वारा बने प्रतिबिम्ब की प्रकृति, स्थिति तथा आपेक्षिक आकार को बताइये: 
(i) वस्तु अनन्त पर स्थित हो। 
(ii) वस्तु अनन्त तथा लैंस के प्रकाशिक केन्द्र O के बीच स्थित हो।
उत्तर:
दी गई स्थितियों के लिये अवतल लैंस द्वारा बने प्रतिबिम्ब की प्रकृति, स्थिति तथा आपेक्षिक आकार निम्न प्रकार है:  

वस्तु की स्थिति	प्रतिबिम्ब की स्थिति	प्रतिबिम्ब का आपेक्षिक आकार	प्रतिबिम्ब की प्रकृति
अनंत पर	फोकस F1 पर	अत्यधिक छोटा, बिंदु आकार	आभासी तथा सीधा
अनंत तथा लैंस के प्रकाशिक केन्द्र O के बीच	फोकस F1 तथा प्रकाशिक केन्द्र O के बीच	छोटा	आभासी तथा सीधा

उपर्युक्त सारणी से स्पष्ट है कि अवतल लैंस सदैव एक आभासी, सीधा तथा छोटा प्रतिबिंब बनायेगा, चाहे वस्तु की स्थिति कहीं पर भी स्थित हो।

प्रश्न 38. 
गोलीय लैंस में कार्तीय चिन्ह परिपाटी क्या है? 
उत्तर:
गोलीय लैंस में चिन्ह परिपाटी - जब हम लैंसों की सहायता से प्रतिबिम्ब की रचना का अध्ययन करते हैं, तब हम कुछ कार्तीय चिन्ह परिपाटी का प्रयोग करते हैं, जो कि निम्न हैं:

1. समस्त दूरियाँ लैंस के प्रकाशिक केन्द्र से मापी जाती हैं।
2. आपतित किरण की दिशा में मापी गयी दूरियाँ धनात्मक मानी जाती हैं तथा जो दूरियाँ आपतित किरण की विपरीत दिशा में मापी जाती हैं, वे दूरियाँ ऋणात्मक दूरियाँ मानी जाती हैं।
3. मुख्य अक्ष से ऊर्ध्वाधरता ऊपर की ओर मापी जाने वाली दूरी धनात्मक मानी जाती है, जबकि मुख्य अक्ष के ऊर्ध्वाधरता नीचे की ओर मापी गई दूरियाँ ऋणात्मक मानी जाती हैं।

यह चिन्ह परिपाटी नीचे दिये गये चित्र से स्पष्ट है -

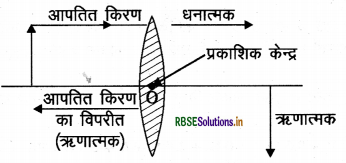
प्रश्न 39. 
आपको एक 20 सेमी. फोकस दूरी का उत्तल लैंस दिया हुआ है। आप वस्तु को कहाँ रखेंगे जिससे उसका वास्तविक, उल्टा और बहुत बड़ा प्रतिबिम्ब बने? चित्र खींचिये।
उत्तर:
वस्तु का प्रतिबिम्ब वास्तविक, उल्टा और बहुत बड़ा बनता है यदि वस्तु को उत्तल लैंस के फोकस पर रखें। अतः वस्तु को लैंस के सामने 20 सेमी. दूरी पर रखा जायेगा।

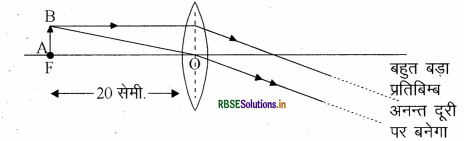
प्रश्न 40. 
दो लैंसों की संयुक्त क्षमता एवं फोकस दूरी को समझाइये।
उत्तर:
माना दो लैंसों की फोकस दूरी क्रमशः। तथा है। जब इन लैंसों को आपस में जोड़ कर रखा जाता है तब यह संयोजन एक लैंस के रूप में कार्य करने लगता है जिसकी फोकस दूरी F है। इस फोकस दूरी (F) को तुल्य फोकस दूरी कहते हैं, जो निम्नलिखित है - 
\(\frac{1}{\mathrm{~F}}=\frac{1}{f_{1}}+\frac{1}{f_{2}}\)
चूँकि \(\frac{1}{f}\)  = P जबकि P लैंस की क्षमता है। अतः दो लैंसों की संयोजन क्षमता निम्नवत् है -
P = P₁ + P₂
जबकि P = \(\frac{1}{\mathrm{~F}}\), P₁ =\(\frac{1}{f_{1}}\) तथा P₂ = \(\frac{1}{f_{2}} \)
यदि P₁, P₂, P₃, P₄....... क्षमताओं के लैंसों को एक - दूसरे से मिलाकर रख दिया जाये तब संयुक्त लैंस की क्षमता निम्नवत् होगी -
P = P₁ + P₂ + P₃ + P₄ + .......

प्रश्न 41. 
एक उत्तल लैंस को एक अवतल लैंस के साथ मिलाकर रखा जाता है और इस संयुक्त लैंस की क्षमता धनात्मक है तो बताइये कि संयुक्त लैंस किस लैंस की तरह से कार्य करेगा?
उत्तर:
चूँकि संयुक्त लैंस की क्षमता धनात्मक है अर्थात् संयुक्त लैंस की फोकस दूरी का मान धनात्मक है। अतः यह उत्तल लैंस की तरह से कार्य करेगा।

प्रश्न 42. 
यदि एक उत्तल लैंस को एक अवतल लैंस के साथ मिलाकर रखा जाये तथा इस संयुक्त लैंस की क्षमता ऋणात्मक हो, तब संयुक्त लैंस किस लैंस की तरह कार्य करेगा?
उत्तर:
चूँकि संयुक्त लैंस की क्षमता का मान ऋणात्मक है, अतः संयुक्त लैंस की फोकस दूरी का मान ऋणात्मक होगा। इस कारण से संयुक्त लैंस अवतल लैंस की तरह कार्य करेगा।

निबन्धात्मक प्रश्न

प्रश्न 1. 
विभिन्न किरणों के आधार पर गोलीय दर्पणों द्वारा बने प्रतिबिंबों के स्थान का निर्धारण किरण आरेख बनाकर कीजिए।
उत्तर:
गोलीय दर्पणों द्वारा किसी बिंब के बने प्रतिबिंब के स्थान निर्धारण के लिए बिंब के किसी बिंदु से निकलने वाली किरणों की विशाल संख्या में से सुविधानुसार कुछ को चुना जा सकता है। तथापि किरण आरेख की स्पष्टता के लिए दो किरणों पर विचार करना अधिक सुविधाजनक है। प्रतिबिंब के स्थान निर्धारण के लिए निम्न में से किन्हीं भी दो किरणों पर विचार किया जा सकता है:

1. दर्पण के मुख्य अक्ष के समांतर प्रकाश किरण, परावर्तन के पश्चात् अवतल दर्पण के मुख्य फोकस से गुजरेगी अथवा उत्तल दर्पण के मुख्य फोकस से अपसरित होती प्रतीत होगी।

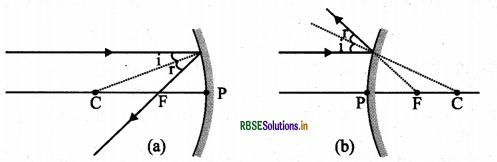
2. अवतल दर्पण के मुख्य फोकस से गुजरने वाली किरण अथवा उत्तल दर्पण के मुख्य फोकस की ओर निर्देशित किरण परावर्तन के पश्चात् मुख्य अक्ष के समांतर निकलेगी।

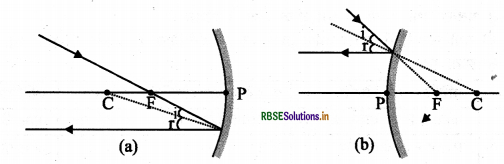
3. अवतल दर्पण के वक्रता केन्द्र से गुजरने वाली किरण अथवा उत्तल दर्पण के वक्रता केन्द्र की ओर निर्देशित किरण, परावर्तन के पश्चात् उसी पथ के अनुदिश वापस परावर्तित हो जाती है।

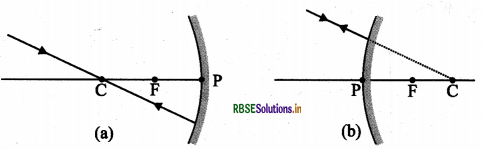
4. अवतल दर्पण अथवा उत्तल दर्पण के ध्रुव (P) की ओर मुख्य अक्ष से तिर्यक दिशा में आपतित किरण, तिर्यक दिशा में ही परावर्तित होती है।

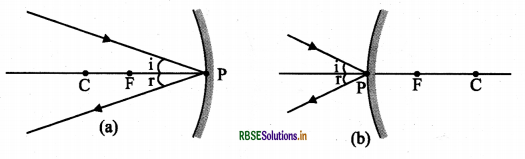
प्रश्न 4. 
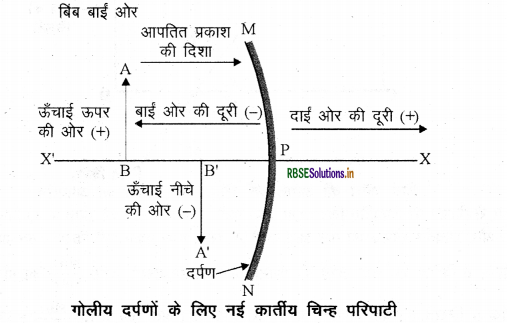
गोलीय दर्पणों के लिये नयी कार्तीय चिन्ह परिपाटी से आप क्या समझते हैं? चित्र बनाकर इसको विस्तार से समझाइये।
उत्तर:
गोलीय दर्पणों के द्वारा प्रकाश के परावर्तन के समय हम एक निश्चित चिन्ह परिपाटी का पालन करते हैं, जिसे नयी कार्तीय चिन्ह परिपाटी कहते हैं। इसमें दर्पण के ध्रुव P को मूलबिन्दु लेते हैं। दर्पण के मुख्य अक्ष को निर्देशांक पद्धति का x-अक्ष (xx') लिया जाता है। परिपाटी अग्र प्रकार है: 

1. वस्तु को दर्पण के बायीं ओर रखा जाता है। इसका अर्थ है कि दर्पण पर वस्तु से प्रकाश बायीं ओर से आपतित होता है। 
2. मुख्य अक्ष के समान्तर सभी दूरियाँ दर्पण के ध्रुव से मापी जाती हैं।
3. मूलबिन्दु के दायीं ओर (+x-अक्ष के अनुदिश) की दूरियाँ धनात्मक और बायीं ओर (-x-अक्ष के अनुदिश) की दूरियाँ ऋणात्मक लेते हैं। 
4. मुख्य अक्ष के लम्बवत् तथा ऊपर की ओर (+y-अक्ष के अनुदिश) मापी जाने वाली दूरियाँ धनात्मक मानी जाती हैं।
5. मुख्य अक्ष के लम्बवत् तथा नीचे की ओर (-y-अक्ष के अनुदिश) मापी जाने वाली दूरियाँ ऋणात्मक मानी जाती हैं।

नयी कार्तीय चिन्ह परिपाटी को नीचे चित्र में दर्शाया गया है:

प्रश्न 5. 
प्रकाश का अपवर्तन क्या है? अपवर्तन का कारण क्या है? किरण चित्र की सहायता से अपवर्तन के नियम समझाइये।
उत्तर:
अपवर्तन:
जब प्रकाश किरण एक माध्यम से दूसरे माध्यम में प्रवेश करती है तो दोनों माध्यमों को पृथक् करने वाले धरातल पर वह अपने मार्ग से विचलित हो जाती है। प्रकाश की इस क्रिया को अपवर्तन कहते हैं । अपवर्तन प्रकाश के एक माध्यम से दूसरे में प्रवेश करने पर प्रकाश की चाल में परिवर्तन के कारण होता है।
अपवर्तन का कारण: दोनों माध्यमों में प्रकाश का वेग अलग - अलग होने के कारण ही प्रकाश का अपवर्तन होता है।

अपवर्तन के नियम:
1.  प्रथम नियम: आपतित किरण, अपवर्तित किरण तथा दोनों माध्यमों को पृथक् करने वाले पृष्ठ के आपतन बिन्दु पर अभिलम्ब तीनों एक ही तल में होते हैं।
2. द्वितीय नियम (स्नेल का अपवर्तन नियम): प्रकाश के किसी निश्चित रंग तथा निश्चित माध्यमों के युग्म के लिए आपतन कोण की ज्या (sini) एवं अपवर्तन कोण की ज्या (sin r) का अनुपात निश्चित रहता है। अतः µ  =\( \frac{\sin i}{\sin r}\) µ एक स्थिरांक है। इस स्थिरांक के मान को दूसरे माध्यम का पहले माध्यम के सापेक्ष अपवर्तनांक (refractive index) कहते हैं।

अपवर्तन के नियमों का सत्यापन:
अपवर्तन के प्रथम नियम की पुष्टि के लिये चित्रानुसार काँच की एक आयताकार सिल्ली ABCD लेते हैं। सिल्ली को सफेद कागज पर रखते हैं। PQ प्रकाश की एक किरण है जो सिल्ली के एक फलक AB पर (कागज के तल को स्पर्श करती हुई) आपतित है। जब बिन्दु Q पर यह काँच में प्रवेश करती है तब अपनी मूल दिशा से विचलित होकर QR दिशा में अपवर्तित हो जाती है, तदुपरान्त RS दिशा में सिल्ली से बाहर निकल जाती है।

QR और RS को क्रमशः अपवर्तित एवं निर्गत किरण कहते हैं। हम देखते हैं कि आपतित किरण PQ, अपवर्तित किरण QR तथा अभिलम्ब QN तीनों विभिन्न तल में न होकर कागज के एक तल में ही हैं। अर्थात् आपतित किरण, अपवर्तित किरण तथा अभिलम्ब तीनों एक ही तल में होते हैं। यही अपवर्तन का पहला नियम है।

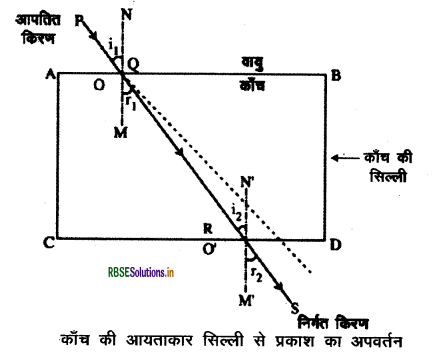
Q को R से मिलाने पर अपवर्तित किरण QR प्राप्त होती है। अब सिल्ली की सतह पर Q बिन्दु से अभिलम्ब खींचकर आपतन कोण । और अपवर्तन कोण r का मान ज्ञात करते हैं। सिल्ली पर प्रकाश की किरण अलग - अलग कोण पर आपतित करते हुए । और r के विभिन्न मान ज्ञात करते हैं। गणना करने पर हम देखते हैं कि \(\frac{\sin i}{\sin r}\) का मान सदैव निश्चित रहता है। इसे स्थिरांक " लिखते हैं। यही अपवर्तन का दूसरा नियम है। अतः ₁µ₂ या µ₁₂ \(\frac{\sin i}{\sin r}\) = एक नियतांक । 

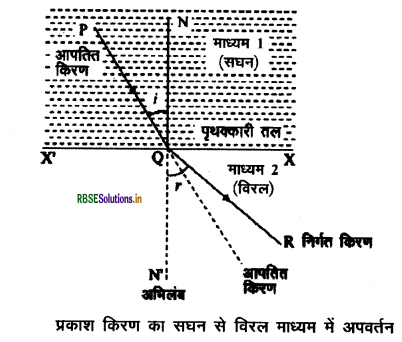
प्रश्न 6. 
प्रकाश के सघन माध्यम से विरल माध्यम में अपवर्तन का किरण आरेख बनाइए। 

प्रश्न 7. 
माध्यम के अपवर्तनांक को परिभाषित कीजिये। इसको प्रभावित करने वाले तीन कारक लिखिये।
उत्तर:
जब प्रकाश की किरण तिरछी गमन करती हुई एक पारदर्शी माध्यम से दूसरे में प्रवेश करती है तो यह दूसरे माध्यम में अपनी दिशा परिवर्तित कर लेती है। किन्हीं दिये हुए माध्यमों के युग्म के लिये होने वाले दिशा परिवर्तन के विस्तार को अपवर्तनांक के रूप में व्यक्त किया जाता है।

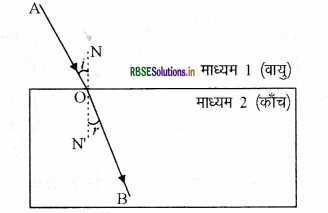
चित्रानुसार प्रकाश की एक किरण माध्यम 1 से माध्यम 2 में प्रवेश कर रही है। माना प्रकाश की चाल माध्यम 1 में तथा माध्यम 2 में v₂ है। माध्यम 2 का माध्यम 1 के सापेक्ष अपवर्तनांक, माध्यम 1 में प्रकाश की चाल तथा माध्यम 2 में प्रकाश की चाल के अनुपात द्वारा व्यक्त करते हैं। इसे प्रायः संकेत n₂₁ से निरूपित करते हैं। अतः
n₂₁ = =\(\frac{v_{1}}{v_{2}}\)

इसी तर्क से, माध्यम 1 का माध्यम 2 के सापेक्ष अपवर्तनांक n₁₂ से निरूपित करते हैं। इसे निम्न प्रकार व्यक्त किया जाता है: 
n₁₂ = =\(\frac{v_{2}}{v_{1}}\)

यदि माध्यम 1 निर्वात या वायु है, तब माध्यम 2 का अपवर्तनांक निर्वात के सापेक्ष माना जाता है। यह माध्यम का निरपेक्ष अपवर्तनांक कहलाता है। यह केवल n₂ से निरूपित किया जाता है। यदि वायु में प्रकाश की चाल c है तथा माध्यम में प्रकाश की चाल v है तब माध्यम का अपवर्तनांक nm होगा: 
n_m ==\(\frac{c}{v}\)

माध्यम का निरपेक्ष अपवर्तनांक केवल अपवर्तनांक कहलाता है। अपवर्तनांक को प्रभावित करने वाले कारक निम्न हैं:

1. माध्यम की प्रकृति, 
2. घनत्व तथा 
3. प्रकाश का रंग। 

प्रश्न 8. 
विभिन्न किरणों के आधार पर लैंसों द्वारा बने प्रतिबिंबों के स्थान का निर्धारण किरण आरेख बनाकर कीजिए। 
उत्तर:
लैंसों में किरण आरेख बनाने के लिए निम्न में से किन्हीं दो किरणों पर विचार कर सकते हैं:
1. बिंब से मुख्य अक्ष के समांतर आने वाली कोई प्रकाश किरण उत्तल लेंस से अपवर्तन के पश्चात् लेंस के दूसरी ओर मुख्य फोकस से गुजरेगी जबकि अवतल लेंस की स्थिति में लेंस के उसी ओर स्थित मुख्य फोकस से अपसरित होती प्रतीत होती है।

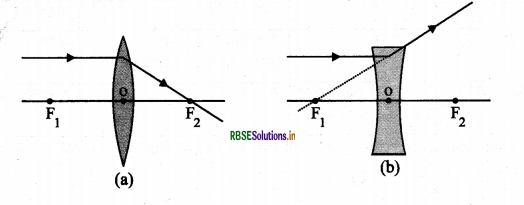
2. मुख्य फोकस से गुजरने वाली प्रकाश किरण, उत्तल लैंस से अपवर्तन के पश्चात् मुख्य अक्ष के समांतर निर्गत होगी। अवतल लेंस के मुख्य फोकस पर मिलती प्रतीत होने वाली प्रकाश किरण, अपवर्तन के पश्चात् मुख्य अक्ष के समांतर निर्गत होगी।

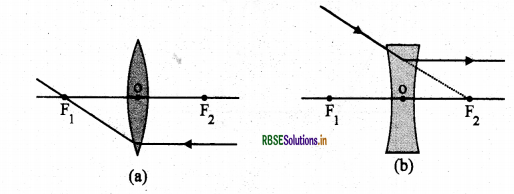
3. लेंस के प्रकाशिक केन्द्र से गुजरने वाली प्रकाश किरण अपवर्तन के पश्चात् बिना किसी विचलन के निर्गत होती है।

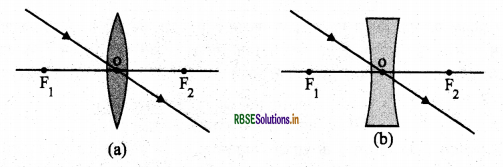
प्रश्न 9. 
विभिन्न स्थितियों में रखी वस्तु का उत्तल लैंस से प्रतिबिम्ब का बनना आरेखित कीजिये
1. अनन्त पर 
2.  2F₁ से परे 
3.  2F₁ पर 
4.  F₁ तथा 2F₁ के बीच 
5. फोकस F₁ पर 
6. फोकस F₁ तथा प्रकाशिक केन्द्र O के बीच।
उत्तर:
वस्तु की विभिन्न स्थितियों के लिये उत्तल लैंस द्वारा बने प्रतिबिम्ब की प्रकृति, स्थिति तथा आपेक्षिक आकार के बारे में नीचे दी गयी सारणी में बताया गया है: 

वस्तु की स्थिति	प्रतिबिम्ब की स्थिति	प्रतिबिम्ब का आपेक्षिक आकार	प्रतिबिम्ब की प्रकृति
1. अनंत पर	फोकस F2 पर	अत्यधिक छोटा, बिंदु आकार	वास्तविक तथा उल्टा
2. 2F1 से परे	F2 तथा 2F2 के बीच	छोटा	वास्तविक तथा उल्टा
3.  2F1 पर	2F2 पर	बड़ा (विवर्धित)	वास्तविक तथा उल्टा
4. F1 तथा 2F1 के बीच	2F2 से परे	बड़ा (विवर्धित)	वास्तविक तथा उल्टा
5.फोकस F1 पर	अनंत पर	असीमित रूप से बड़ा अथवा अत्यधिक विवर्धित	वास्तविक तथा उल्टा
6. फोकस F1 तथा प्रकाशिक  केन्द्र O के बीच	जिस ओर बिंब हैं लैंस के उसी ओर	बड़ा (विवर्धित)	आभासी तथा सीधा

नीचे दिये गये चित्रों में उत्तल लैंस द्वारा किसी वस्तु की विभिन्न स्थितियों में प्रतिबिम्ब बनने को किरण आरेखों द्वारा दर्शाया गया है -

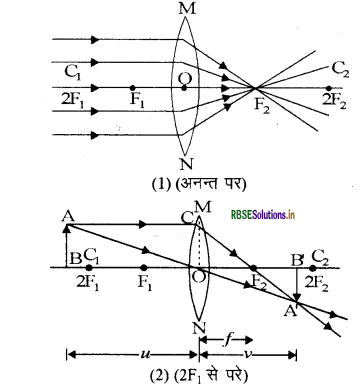
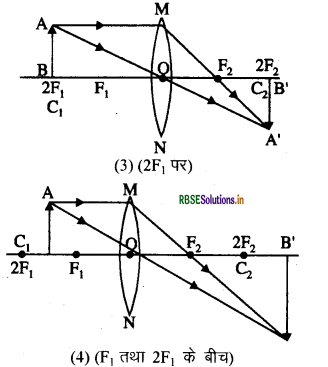
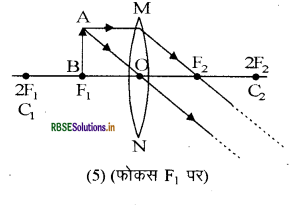
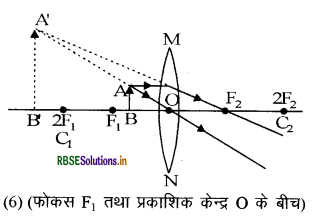
प्रश्न 10. 
प्रकाश के लिए 'सघन माध्यम' एवं 'विरल माध्यम' से क्या तात्पर्य है? समझाइए।
उत्तर:
किसी माध्यम की प्रकाश को अपवर्तित करने की क्षमता को इसके प्रकाशिक घनत्व के द्वारा भी व्यक्त किया जा सकता है। प्रकाशिक घनत्व का एक निश्चित संपृक्तार्थ होता है। यह द्रव्यमान घनत्व के समान नहीं है। इसलिए सघन माध्यम एवं विरल माध्यम से अर्थ 'प्रकाशिक सघन माध्यम' तथा 'प्रकाशिक विरल माध्यम' है। दो माध्यमों की तुलना करते समय, अधिक अपवर्तनांक वाला माध्यम दूसरे की अपेक्षा प्रकाशिक सघन माध्यम है।

दूसरा कम अपवर्तनांक वाला माध्यम प्रकाशिक विरल माध्यम है। विरल माध्यम में प्रकाश की चाल सघन माध्यम की अपेक्षा अधिक होती है। अतः विरल माध्यम से सघन माध्यम में गमन करने वाली प्रकाश की किरण धीमी हो जाती है तथा अभिलंब की ओर झुक जाती है। जब ये सघन माध्यम से विरल माध्यम में गमन करती है तो इसकी चाल बढ़ जाती है तथा यह अभिलंब से दूर हट जाती है।

प्रश्न 11. 
निम्न लैंसों के प्रकाशिक केन्द्र से 21 तथा दूरी के मध्य स्थित किसी बिन्दु पर स्थित बिम्ब का प्रतिबिम्ब बनाने के लिए किरण चित्र बनाइए तथा प्रतिबिम्बों की प्रकृति लिखिए:
(अ) उत्तल लैंस
(ब) अवतल लैंस 
यहाँ f₁ दिए गए लैंस की फोकस दूरी है। 
उत्तर:
उत्तल लैंस के प्रकाशिक केन्द्र 2F₁ तथा F₁ दूरी के मध्य स्थित किसी बिन्दु पर स्थित बिम्ब का प्रतिबिम्ब: 

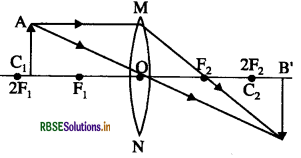
यह प्रतिबिम्ब वास्तविक, उल्टा तथा बड़ा बनता है। 

अवतल लैंस के प्रकाशिक केन्द्र 2F₁ तथा F₁ दूरी के मध्य स्थित किसी बिन्दु का प्रतिबिम्ब:

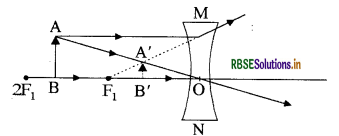
यह प्रतिबिम्ब आभासी, सीधा तथा छोटा बनेगा।

आंकिक प्रश्न
प्रश्न 1. 
एक अवतल लैंस की फोकस दूरी 40 सेमी है। इसकी क्षमता क्या होगी?
उत्तर:
लैंस की क्षमता P = \(\frac{1}{f}\) मीटर 
यहाँ
f = -40 सेमी 
P = \( -\frac{100}{40}\)
P = -2.5D 

प्रश्न 2. 
किसी ऑटोमोबाइल में पीछे का दृश्य देखने के लिये उपयोग होने वाले उत्तल दर्पण की वक्रता त्रिज्या 3.00 m है। यदि एक बस इस दर्पण से 5.00 m की दूरी पर स्थित है, तो प्रतिबिम्ब की स्थिति, प्रकृति तथा साइज ज्ञात कीजिये।
उत्तर:
दिया गया है:
उत्तल दर्पण की वक्रता त्रिज्या R = + 3.00 m 
(वस्तु की दूरी) बिंब की दूरी u =  -5.00 m (चिन्ह परिपाटी से) 
प्रतिबिंब की दूरी v  = ? 
प्रतिबिंब की ऊँचाई h' = ?
हम जानते हैं फोकस दूरी f = \(\frac{R}{2}\)
f = \(\frac{+3.00 m}{2}\) = +1.50m
दर्पण सूत्र
\(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
∴\(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}\)
मान रखने पर
\(\begin{aligned} \frac{1}{v} &=\frac{1}{1.50}-\left(-\frac{1}{5.00}\right) \\ \frac{1}{v} &=\frac{1}{1.50}+\frac{1}{5}=\frac{100}{150}+\frac{1}{5} \\ \frac{1}{v} &=\frac{2}{3}+\frac{1}{5}=\frac{10+3}{15}=\frac{13}{15} \\ v &=\frac{15}{13}=1.15 \mathrm{~m} \end{aligned}\)

अतः प्रतिबिम्ब दर्पण के पीछे 1.15 m की दूरी पर स्थित है।
आवर्धन (m) = \( \frac{h^{\prime}}{h}=-\frac{1}{u}\)
मान रखने पर
m = \( -\left(\frac{1.15 \mathrm{~m}}{-5.00 \mathrm{~m}}\right)\)
m = \( \frac{115}{500}\) = +0.23 
यहाँ पर आवर्धन का मान धनात्मक चिन्ह का है। अतः प्रतिबिम्ब आभासी, सीधा तथा साइज में बिंब से छोटा (0.23 गुना) है।

प्रश्न 3. 
यदि कोई नेत्र चिकित्सक + 2.5 D तथा –4.0 D क्षमता के संशोधक लैंस निर्धारित करता है तो लैंस की प्रकृति व फोकस दूरी ज्ञात कीजिए। 
उत्तर:
लैंस क्षमता P =\( \frac{1}{f}\) मीटर 

(i) जहाँ
P = +2.5D 
2.5 = \(\frac{1}{f}\)
∴ f = \(\frac{1}{2.5} \)मीटर
\(\frac{100}{2.5}\) सेमी.
= + 40 सेमी.
अतः धनात्मक चिह्न दर्शाता है कि लेंस उत्तल लेंस होगा जिसकी फोकस दूरी 40 सेमी है। 

(ii) जब
P = -4.0D
-4.0 = \( \frac{1}{f}\)
f = \(\frac{1}{-4.0}\)मीटर
   = \(-\frac{100}{4}\) सेमी.
f = -25 सेमी. 
अतः ऋणात्मक चिह्न दर्शाता है कि लेंस अवतल लेंस होगा जिसकी फोकस दूरी 25 सेमी है।

प्रश्न 4.
12 cm फोकस दूरी के एक अवतल दर्पण के सामने 4 cm लम्बाई की एक वस्तु (Object) उससे 6 cm की दूरी पर रखी गयी है। प्राप्त प्रतिबिम्ब की स्थिति, प्रकृति तथा उसका आकार ज्ञात कीजिये। 
उत्तर:
दिया गया है:
u = - 6 cm (चिन्ह परिपाटी)
f = - 12 cm (चिन्ह परिपाटी) 
वस्तु का आकार h' = 4 cm 
दर्पण सूत्र से:
\(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)
मान रखने पर
\(-\frac{1}{6}+\frac{1}{v}=-\frac{1}{12}\)
या\( \begin{aligned} &\frac{1}{v}=-\frac{1}{12}+\frac{1}{6}=\frac{-1+2}{12} \\ &\frac{1}{v}=\frac{1}{12} \end{aligned} \)
v = 12 cm 
अतः प्रतिबिम्ब दर्पण के पीछे, उससे 12 cm की दूरी पर बना है। यहाँ पर v का मान धनात्मक है। अतः प्रतिबिम्ब कल्पित प्रकृति का है।

आवर्धन क्षमता सूत्र:
m =\( \frac{h^{\prime}}{h}=-\frac{v}{u}\)
\(\begin{aligned} \frac{h^{\prime}}{h} &=-\frac{v}{u} \\ h^{\prime} &=-\left(\frac{v}{u}\right) \times h \end{aligned}\)

मान रखने पर:
\(-\left(\frac{12}{-6}\right) \times 4\)
= 8 cm 
अतः बिम्ब की लम्बाई 8 cm है। यहाँ पर चिन्ह धनात्मक है। अतः प्रतिबिम्ब सीधा है।

प्रश्न 5. 
अवतल दर्पण के सामने रखे एक बिम्ब का प्रतिबिंब दर्पण के सामने 100 सेमी पर बनता है। यदि दर्पण की फोकस दूरी 98 सेमी. हो तो बिम्ब की दूरी ज्ञात करो।
उत्तर:
दर्पण सूत्र:
\(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)
यहाँ
f= -98 सेमी 
 v = -100 सेमी 
 u = ?
मान रखने पर:
\(\begin{aligned} \frac{1}{-98} &=\frac{1}{u}+\frac{1}{-100} \\ \frac{1}{u} &=\frac{1}{100}-\frac{1}{98} \\ &=-\frac{1}{4900} \end{aligned}\)
u = - 4900 सेमी. 

प्रश्न 6. 
किसी गतिमान वाहन में प्रयुक्त उत्तल दर्पण की वक्रता त्रिज्या 2.0 m है। इस वाहन के पीछे 3.5 m की दूरी पर एक ट्रक आ रहा है। ज्ञात कीजिये 
(i) प्रतिबिम्ब की स्थिति 
(ii) ट्रक के सापेक्ष उसके प्रतिबिम्ब का आकार/प्रतिबिम्ब की प्रकृति (Nature) क्या होगी? 
उत्तर:
प्रश्नानुसार:
वक्रता त्रिज्या R = 2.0 m
∵ R = 2f
∴  f = \(\frac{\mathrm{R}}{2}=\frac{2.0}{2}=1\)m
u = -3.5 m (चिन्ह परिपाटी से)
दर्पण सूत्र: 
\(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)
\(\begin{aligned} \frac{1}{v} &=\frac{1}{f}-\frac{1}{u} \\ &=\frac{1}{1}-\left(-\frac{1}{3.5}\right)=1+\frac{1}{3.5} \\ &=1+\frac{10}{35}=1+\frac{2}{7}=\frac{7+2}{7}=\frac{9}{7} \end{aligned}\)
v=\(\frac{7}{9}=0.78 \mathrm{~m}\)
 
अतः उत्तल दर्पण में ट्रक 0.78 m की दूरी पर दिखाई देगा। प्रतिबिम्ब का आकार और प्रकृति का मान निम्न सूत्र से ज्ञात करते हैं: 
m = \(-\frac{v}{u}\)
= \(-\left(\frac{\frac{7}{9}}{-3.5}\right)=\frac{7}{9} \times \frac{1}{3.5}=\frac{2}{9}\)

अतः ट्रक के प्रतिबिम्ब का आकार उसके आकार\( \frac{2}{9}\) गुना है। यहाँ पर m का मान धनात्मक है। अतः प्रतिबिम्ब कल्पित एवं सीधा है।

प्रश्न 7. 
सघन फ्लिंट ग्लास का अपवर्तनांक 1.65 है तथा ऐल्कोहल का वायु के सापेक्ष अपवर्तनांक 1.36 है, तब फ्लिंट ग्लास का ऐल्कोहल के सापेक्ष अपवर्तनांक का मान ज्ञात कीजिये। 
उत्तर:
दिया गया है-
n_g = 1.65
तथा
n_al = 1.36
∴  \({ }^{a l} n_{g}=\frac{n_{g}}{n_{a l}}=\frac{1.65}{1.36}\) = 1.213

प्रश्न 8. 
एक अवतल दर्पण के सामने 15 सेमी. की दूरी पर कोई वस्तु रखी है। दर्पण द्वारा बने प्रतिबिम्ब की प्रकृति, स्थिति व आवर्धन ज्ञात करो। दर्पण की फोकस दूरी 10 सेमी. है।
उत्तर:
दर्पण सूत्र:
\(​​​​​​​ \frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)
u = -15 सेमी
f = -10 सेमी 
v = ?
\(\begin{aligned} \frac{1}{-10} &=\frac{1}{v}+\frac{1}{-15} \\ \frac{1}{v} &=\frac{1}{15}-\frac{1}{10} \\ &=-\frac{1}{30} \end{aligned}\)
v = -30 सेमी. 
अर्थात् प्रतिबिम्ब दर्पण की बायीं ओर बनेगा तथा वास्तविक एवं उल्टा होगा।

प्रश्न 9. 
प्रकाश वायु से काँच में प्रवेश करता है, जिसका अपवर्तनांक 1.5 है। 50 सेमी. मोटे काँच के गुटके को पार करने में प्रकाश का लगा समय ज्ञात करो। 
उत्तर:
दिया गया है:
प्रकाश का वायु में वेग c = 3 x 10⁸ m/s 
काँच का अपवर्तनांक n = 1.5
चूंकि अपवर्तनांक n = \( \frac{c}{v}\)
∴ v = \(\frac{c}{n}\)

मान रखने पर
v = \(\frac{3 \times 10^{8}}{1.5}\)  = 2x10⁸ m/s 
अतः प्रकाश का काँच में वेग = 2 x 10⁸ m/s

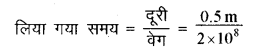
= 2.5 x 10^-9 से

प्रश्न 10. 
किसी अवतल लैंस की फोकस दूरी 15 cm है। बिंब को लैंस से कितनी दूरी पर रखें कि इसके द्वारा बिंब का लैंस से 10 cm दूरी पर प्रतिबिंब बने? लैंस द्वारा उत्पन्न आवर्धन भी ज्ञात कीजिए।
उत्तर:
हम जानते हैं कि अवतल लैंस में सदैव ही आभासी, सीधा प्रतिबिंब उसी ओर बनता है जिस तरफ बिंब रखा हुआ होता है। 
दिया गया है- 
प्रतिबिंब की दूरी v = - 10 cm
फोकस दूरी f = - 15 cm
बिंब की दूरी u = ? 
लैंस सूत्र से:
\(\begin{aligned} \frac{1}{v}-\frac{1}{u} &=\frac{1}{f} \\ \frac{1}{u} &=\frac{1}{v}-\frac{1}{f} \end{aligned}\)

मान रखने पर:
\(\begin{aligned} &\frac{1}{u}=-\frac{1}{10}-\left(-\frac{1}{15}\right)=\frac{-1}{10}+\frac{1}{15} \\ &\frac{1}{u}=\frac{-3+2}{30}=\frac{-1}{30} \end{aligned}\)
u = -30 cm
अतः बिंब की दूरी 30 cm है।

आवर्धन:
m = \( \frac{v}{u}\)
m = \(\frac{-10 \mathrm{~cm}}{-30 \mathrm{~cm}}=\frac{1}{3}\) = +0.33
यहाँ पर धनात्मक चिन्ह यह दर्शाता है कि प्रतिबिम्ब सीधा तथा आभासी है। प्रतिबिम्ब का आकार बिंब के आकार का एक - तिहाई है।

प्रश्न 11. 
एक अवतल दर्पण से बिम्ब का तीन गुना बड़ा आभासी प्रतिबिम्ब प्राप्त होता है। दर्पण की वक्रता त्रिज्या 36 सेमी है। वस्तु की स्थिति ज्ञात करो।
उत्तर:
माना कि वस्तु दर्पण से x दूरी पर स्थित है। अतः
आवर्धन सूत्र से:  
m = \(-\frac{v}{u}\)
m = + 3
u = -x सेमी.

मान रखने पर:
\(3=\frac{-v}{-x}\)
v = 3x

दर्पण सूत्र से:
\(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)
R = -36 सेमी.
\(f=\frac{R}{2}\)
\(\begin{aligned} f &=\frac{-36}{2}=-18 \\ \frac{1}{-18} &=\frac{1}{3 x}-1 \end{aligned}\)
x = 12 सेमी
u = -12 सेमी. 

प्रश्न 12. 
कोई 2.0 cm लंबा बिंब 10 cm फोकस दूरी के किसी उत्तल लैंस के मुख्य अक्ष के लंबवत रखा है। बिंब की लैंस से दूरी 15 cm है। प्रतिबिंब की प्रकृति, स्थिति तथा साइज ज्ञात कीजिए। इसका आवर्धन भी ज्ञात कीजिए। 
उत्तर:
बिंब की ऊँचाई h = + 2.0 cm
फोकस दूरी f = + 10 cm
बिंब-दूरी  u = – 15 cm
प्रतिबिंब-दूरी v = ?
प्रतिबिंब की ऊँचाई h' = ? 
लैंस के सूत्र से:
\(\begin{aligned} \frac{1}{v}-\frac{1}{u} &=\frac{1}{f} \\ \frac{1}{v} &=\frac{1}{u}+\frac{1}{f} \end{aligned}\)
मान रखने पर:
\(\begin{aligned} \frac{1}{v}-\frac{1}{u} &=\frac{1}{f} \\ \frac{1}{v} &=\frac{1}{u}+\frac{1}{f} \end{aligned}\)
v= + 30 cm 
v का धनात्मक मान यह बताता है कि प्रतिबिम्ब लैंस के प्रकाशिक केन्द्र के दायीं ओर 30 cm दूरी पर बनता है।अतः प्रतिबिम्ब वास्तविक तथा उल्टा है।
या
आवर्धन, m  =\(\frac{h^{\prime}}{h}=\frac{v}{u}\)
अथवा h'  =\(\left(\frac{v}{u}\right) \times h\)
मान रखने पर:
\(h^{\prime}=\left(\frac{+30}{-15}\right) \times 2.0\)
h' = -4.0 cm
प्रतिबिम्ब की ऊँचाई:
h' = -4.0 cm
आवर्धन, m = \(\frac{+30 \mathrm{~cm}}{-15 \mathrm{~cm}}\) = -2 
m तथा h' के ऋणात्मक चिन्ह यह बताते हैं कि प्रतिबिम्ब उल्टा तथा वास्तविक है। यह मुख्य अक्ष के नीचे बनता है। इस प्रकार एक वास्तविक, उल्टा तथा 4.0 cm लम्बा प्रतिबिम्ब लैंस के दायीं ओर लैंस से 30 cm दूरी पर बनता है। यह प्रतिबिम्ब दोगुना विवर्धित है।

प्रश्न 13.
5D क्षमता के अभिसारी लैंस को 3 D क्षमता के अपसारी लैंस से सटाकर रखा गया है। संयुक्त लैंस की फोकस दूरी का मान ज्ञात कीजिये। 
उत्तर:
अभिसारी लैंस या उत्तल लैंस की क्षमता
P₁  = 5 D 
अपसारी लैंस (अवतल लैंस) की क्षमता
P₂ = - 3 D 
संयुक्त लैंस की क्षमता P = P₁ + P₂  से
= 5 D -  3 D = 2 D 
लैंस की फोकस दूरी:
f =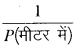=\(\frac{1}{2} \mathrm{~m}\)
f = \(\frac{1}{2}m \) = 50 cm 
संयुक्त लैंस उत्तल लैंस की तरह से कार्य करेगा।

प्रश्न 14. 
एक अवतल दर्पण के ध्रुव से 15 सेमी. दूरी पर रखे बिंब का दो गुना आवर्धित एवं वास्तविक प्रतिबिम्ब बनता है। दर्पण से प्रतिबिम्ब की दूरी एवं दर्पण की फोकस दूरी ज्ञात कीजिए। 
उत्तर:
यहाँ दिया गया है- 
u = - 15 cm
आवर्धन (m) = 2 = \( +\frac{v}{u}\) (प्रतिबिम्ब वास्तविक है)
अतः
2 = \(\frac{v}{-15}\)
अवतल दर्पण से प्रतिबिम्ब की दूरी v  = 2 x – 15 = -  30 cm उत्तर 
गोलीय दर्पण सूत्र: 
\(\begin{aligned} &\frac{1}{f}=\frac{1}{v}+\frac{1}{u} \\ &\frac{1}{f}=-\frac{1}{30}-\frac{1}{15} \\ &\frac{1}{f}=\frac{-1-2}{30}=\frac{-3}{30} \end{aligned}\)
f = - 10 cm 
अतः दर्पण की फोकस दूरी - 10 सेमी. होगी। 

प्रश्न 15. 
वायु के सापेक्ष काँच का अपवर्तनांक \(\frac{3}{2}\) है तथा वायु के सापेक्ष जल का अपवर्तनांक है। यदि वायु में प्रकाश की चाल 3x 10⁸ m/s है, तो 
(a) काँच में 
(b) जल में, प्रकाश की चाल ज्ञात कीजिए।
उत्तर:
दिया हुआ है-
n_g = \(\frac{3}{2} \)
तथा
n_w = \(\frac{4}{3} \)

(c) वायु में प्रकाश की चाल = 3 x 10⁸ m/s है। 
हम जानते हैं कि:
n_g= 

अतः v (काँच में प्रकाश की चाल) = \(\frac{c}{n_{g}}\)
=\(\begin{aligned} &=\frac{3 \times 10^{8}}{\frac{3}{2}} \\ &=\frac{3 \times 10^{8} \times 2}{3} \end{aligned}\)
= 2 x 10⁸ m/s 
वायु में प्रकाश की चाल पुनः 

n_w = =\(\frac{c}{v}\)
 अतः v  (जल में प्रकाश की चाल) = \(\frac{C}{n_{w}}\)
\( \begin{aligned} &=\frac{3 \times 10^{8} \times 3}{4} \\ &=\frac{9}{4} \times 10^{8} \end{aligned}\)
 = 2.25 x 10° m/s