RBSE Solutions for Class 9 Science Chapter 9 बल तथा गति के नियम

Rajasthan Board RBSE Solutions for Class 9 Science Chapter 9 बल तथा गति के नियम Textbook Exercise Questions and Answers.

RBSE Class 9 Science Solutions Chapter 9 बल तथा गति के नियम

RBSE Class 9 Science Chapter 9 बल तथा गति के नियम InText Questions and Answers

पृष्ठ 131.

प्रश्न 1. 
अग्र में किसका जड़त्व अधिक है।
(a) एक रबड़ की गेंद एवं उसी आकार का पत्थर 
(b) एक साइकिल एवं एक रेलगाड़ी 
(c) पाँच रुपए का एक सिक्का एवं एक रुपए का सिक्का। 
उत्तर:
चूँकि किसी वस्तु का द्रव्यमान ही उसके जड़त्व की माप होता है।
(a) चूँकि रबर की गेंद की तुलना में उसी के आकार के पत्थर का द्रव्यमान अधिक होगा, अत: गेंद के आकार के पत्थर का जड़त्व भी अधिक होगा।

(b) चूँकि रेलगाड़ी का द्रव्यमान, साइकिल के द्रव्यमान से अधिक है, अतः रेलगाड़ी का जड़त्व भी अधिक होगा।

(c) चूँकि एक रुपए के सिक्के की तुलना में पाँच रुपए के सिक्के का द्रव्यमान अधिक होगा, अतः पाँच रुपए के सिक्के का जड़त्व भी अधिक होगा।

 

प्रश्न 2. 
नीचे दिए गए उदाहरण में गेंद का वेग कितनी बार बदलता है, जानने का प्रयास करें।
"फुटबाल का एक खिलाड़ी गेंद पर किक लगाकर गेंद को अपनी टीम के दूसरे खिलाड़ी के पास पहुँचाता है। दूसरा खिलाड़ी उस गेंद को किक लगाकर गोल की ओर पहुँचाने का प्रयास करता है। विपक्षी टीम का गोलकीपर गेंद को पकड़ता है और अपनी टीम के खिलाड़ी की ओर किक लगाता है।"
इसके साथ ही उस कारक की भी पहचान करें जो प्रत्येक अवस्था में बल प्रदान करता है।
उत्तर:
बल की अवधारणा खींचने, धकेलने और ठोकर लगाने की क्रिया पर आधारित है और यही गति को प्रदान करता है। बल लगाने से वस्तु के वेग का परिमाण, उसकी दिशा में परिवर्तन और आकार में परिवर्तन होता है। ऊपर दिये गये उदाहरण में गेंद का वेग कुल तीन बार बदलता है।

1. पहली बार गेंद के वेग में परिवर्तन, पहले खिलाड़ी के द्वारा गेंद को लगाई गई किक से प्राप्त आवश्यक बल के कारण होता है।
2. दूसरी बार गेंद के वेग में परिवर्तन के लिए आवश्यक बल, दूसरे खिलाड़ी के गेंद को लगाई गई किक से प्राप्त होता है।
3. तीसरी बार गेंद के वेग में परिवर्तन के लिए आवश्यक बल, विपक्षी टीम के गोलकीपर द्वारा गेंद को लगाई गई किक से प्राप्त होता है।

प्रश्न 3. 
किसी पेड़ की शाखा को तीव्रता से हिलाने पर कुछ पत्तियाँ झड़ जाती हैं। क्यों?
उत्तर:
पेड़ की शाखा तथा पत्तियाँ विराम अवस्था में रहती हैं। जब पेड़ की शाखा को तीव्रता से हिलाते हैं, तब शाखा तो तुरन्त गति की स्थिति में आ जाती है परन्तु उससे जुड़ी पत्तियाँ जड़त्व के कारण विरामावस्था में ही बनी रहती हैं। जिस कारण शाखा को तीव्रता से हिलाने पर कुछ पत्तियाँ झड़ जाती हैं।

प्रश्न 4. 
जब कोई गतिशील बस अचानक रुकती है तो आप आगे की ओर झुक जाते हैं और जब विरामावस्था से गतिशील होती है तो पीछे की ओर हो जाते हैं, क्यों?
उत्तर:
ऐसा जड़त्व के कारण होता है। जब हम गतिशील बस में सफर कर रहे होते हैं, तब हमारा शरीर भी बस के साथ उसी वेग से गति कर रहा होता है। जब बस अचानक रुकती है, तब हमारे पैर, जो बस के फर्श के सम्पर्क में थे, तुरंन्त विरामावस्था में आ जाते हैं परन्तु हमारे शरीर का ऊपरी भाग गतिज जड़त्व के कारण इसका विरोध करता है और हम आगे की ओर झुक जाते हैं।

इसके विपरीत जब कोई बस विरामावस्था से गतिशील होती है, तब हमारे पैर, जो बस के फर्श के सम्पर्क में रहते हैं, बस के साथ ही गति में आ जाते हैं। परन्तु हमारे शरीर का ऊपरी भाग स्थिर जड़त्व के कारण इस गति का विरोध करता है, जिस कारण हम पीछे की ओर झुक जाते हैं। 

पृष्ठ 140.

प्रश्न 1. 
यदि क्रिया सदैव प्रतिक्रिया के बराबर है तो स्पष्ट कीजिए कि घोड़ा गाड़ी को कैसे खींच पाता है?
उत्तर:
न्यूटन के तीसरे नियम के अनुसार क्रिया सदैव प्रतिक्रिया के बराबर होती है। घोड़ा - गाड़ी चलते समय घोड़ा, गाड़ी को खींचने के लिए अपने पैरों से सड़क पर पीछे की ओर बल लगाता है अर्थात् घोड़ा नीचे पृथ्वी की सतह को अपने पैरों से पीछे धकेलता है। क्रिया - प्रतिक्रिया नियम के अनुसार सड़क भी घोड़े के पैरों पर उतना ही प्रतिक्रिया बल विपरीत दिशा में लगाती है, जिसके प्रभाव से घोड़ा - गाड़ी चलती है।

प्रश्न 2. 
एक अग्निशमन कर्मचारी को तीव्र गति से बहुतायत मात्रा में पानी फेंकने वाली रबड़ की नली को पकड़ने में कठिनाई क्यों होती है? स्पष्ट करें।
उत्तर:
चूँकि क्रिया और प्रतिक्रिया सदा समान और विपरीत दिशा में होती हैं। जब अग्निशमन कर्मचारी पानी फेंकने वाली रबड़ की नली को पकड़ता है तो उसे कठिनाई होती है क्योंकि पाइप से पानी की धारा उच्च वेग से निकलती है। क्रिया - प्रतिक्रिया नियम के अनुसार, उच्च वेग से निकलता पानी, उतने ही वेग से प्रतिक्रिया बल पाइप पर विपरीत दिशा में लगाता है, जिस कारण अग्निशमन कर्मचारी को पाइप को संभालने में कठिनाई होती है।

प्रश्न 3. 
एक 50g द्रव्यमान की गोली 4 kg द्रव्यमान की रायफल से 35m/s के प्रारंभिक वेग से छोड़ी जाती है। रायफल के प्रारंभिक प्रतिक्षेपित वेग की गणना कीजिए। उत्तर:
हल: दिया गया है, गोली का द्रव्यमान,
m₁ = 50g = \(\frac{50}{1000} \mathrm{~kg}\)
\(\frac{1}{20} \mathrm{~kg}\)
रायफल का द्रव्यमान, m₂ = 4kg 
गोली का प्रारंभिक वेग = U₁ = 0m/s
रायफल का प्रारंभिक वेग = U₂ = 0m/s
गोली का अंतिम वेग V₁ = 35 m/s
रायफल का प्रतिक्षेपित वेग V₂ = ?
∴ गोली से विस्फोट होने से पूर्व, गोली तथा रायफल, दोनों विरामावस्था में थीं,
अतः संवेग संरक्षण के नियम से, गोली छूटने से पहले कुल संवेग = गोली छूटने के बाद कुल संवेग
\(m_{1} u_{1}+m_{2} u_{2}=m_{1} v_{1}+m_{2} v_{2}\)

\(\begin{aligned} \frac{1}{20} \times 0+4 \times 0 &=\frac{1}{20} \times 35+4 \times v_{2} \\ 0+0 &=\frac{7}{4}+4 v_{2} \\ -\frac{7}{4} &=4 v_{2} \end{aligned}\)
\(\therefore v_{2}=\frac{-7}{4 \times 4}=-0.44 \mathrm{~m} / \mathrm{s}\)

ऋणात्मक चिह्न यह दर्शाता है कि रायफल गोली के विपरीत दिशा में प्रतिक्षेपित होगी। अतः रायफल का प्रतिक्षेपित वेग 0.44 मीटर / सेकण्ड पीछे की ओर होगा।

प्रश्न 4. 
100g और 200g द्रव्यमान की दो वस्तुएँ एक ही रेखा के अनुदिश एक ही दिशा में क्रमश: 2 m/s और 1 m/s के वेग से गति कर रही हैं। दोनों वस्तुएँ टकरा जाती हैं। टक्कर के पश्चात् प्रथम वस्तु का वेग 1.67 m/s हो जाता है, तो दूसरी वस्तु का वेग ज्ञात करो।
उत्तर:
दिया गया है, टकराने से पहले प्रथम वस्तु का द्रव्यमान m₁ = 100 g = \(\frac{100}{1000} \mathrm{~kg}\)
∴ m₁ = 0.1kg
टक्कर से पहले प्रथम वस्तु का वेग (u₁) = 2 m/s
टक्कर से पहले दूसरी वस्तु का द्रव्यमान (m₂) = 200 g = \(\frac{200}{1000} \mathrm{~kg}\)
∴ m₂ = 0.2 kg
टक्कर से पहले दूसरी वस्तु का वेग U₂ = 1 m/s
टकराने से पहले का कुल संवेग = m₁u₁ + m₂u₂
मान रखने पर = 0.1 x 2 + 0.2 x 1
= 0.4 kg m/s
टकराने के बाद टक्कर के पश्चात् प्रथम वस्तु का वेग 
V₁ = 1.67 m/s
दसरी वस्तु का वेग V₂ = ?
टकराने के बाद कुल संवेग = m₁V₁ + m₂V₂
= 0.1 x 1.67 + 0.2 x 12
संवेग संरक्षण के नियम से
टक्कर से पूर्व का संवेग = टक्कर के बाद का संवेग अर्थात्
0.4 = 0.1 x 1.67 + 0.2 x 2
0.4 = 0.167 + 0.2 V₂
0.4 - 0.167 = 0.2 V₂
0.233 = 0.2 2
\(v_{2}=\frac{0.233}{0.2}\)
V₂ = 1.165 मीटर/सेकण्ड
अतः टक्कर के बाद दूसरी वस्तु का वेग 1.165 मीटर/सेकण्ड होगा और दूसरी वस्तु, पहली वस्तु की दिशा में ही गति करेगी।

RBSE Class 9 Science Chapter 9 बल तथा गति के नियम Textbook Questions and Answers

प्रश्न 1. 
कोई वस्तु शून्य बाह्य असंतुलित बल अनुभव करती है। क्या किसी भी वस्तु के लिए अशून्य वेग से गति करना संभव है? यदि हाँ, तो वस्तु के वेग के परिमाण एवं दिशा पर लगने वाली शर्तों का उल्लेख करें। यदि नहीं, तो कारण स्पष्ट करें।
उत्तर:
पहली स्थिति में यदि किसी गतिमान वस्तु पर कार्यरत सभी बलों का परिणामी बल शून्य है, तो वस्तु का कुल प्रारम्भिक वेग होता है। इस स्थिति में प्रश्न का उत्तर हाँ सही है। दूसरी स्थिति - यदि वस्तु विराम स्थिति में है तो इस प्रश्न का उत्तर है 'नहीं' क्योंकि न्यूटन की गति के प्रथम नियम से असंतुलित बल की अनुपस्थिति में कोई वस्तु अपनी प्रारम्भिक स्थिति में ही रहती है।

प्रश्न 2. 
जब किसी छड़ से एक दरी (कार्पेट) को पीटा जाता है, तो धूल के कण बाहर आ जाते हैं। स्पष्ट करें।
उत्तर:
जब किसी छड़ से एक दरी को झाड़ा या पीटा जाता है, तब दरी आगे-पीछे गतिशील होती है पर उसमें विद्यमान धूल के कण जड़त्व के कारण अपनी स्थिति बनाये रखना चाहते हैं, जिस कारण वे बाहर आ जाते हैं और नीचे गिर जाते हैं।

प्रश्न 3. 
बस की छत पर रखे सामान को रस्सी से क्यों बाँधा जाता है?
उत्तर:
जब सामान को बस की छत पर रखते हैं तो ये बस के साथ जुड़े हुए नहीं होते हैं। इस स्थिति में, बस जब अचानक चलना शुरू करती है, तो कुछ हल्के सामान बस की छत से पीछे की ओर गिर भी सकते हैं। यदि चलती हुई बस अचानक रुके, तो सामान आगे की ओर गिर सकता है। इसलिए बस की छत के ऊपर सामान को बाँधा जाता है।

प्रश्न 4. 
किसी बल्लेबाज द्वारा क्रिकेट की गेंद को मारने पर गेंद जमीन पर लुढ़कती है। कुछ दूरी चलने के पश्चात् गेंद रुक जाती है। गेंद रुकने के लिए धीमी होती है, क्योंकि
(a) बल्लेबाज ने गेंद को पर्याप्त प्रयास से हिट नहीं किया है।
(b) वेग गेंद पर लगाए गए बल के समानुपाती है। 
(c) गेंद पर गति की दिशा के विपरीत एक बल कार्य कर रहा है। 
(d) गेंद पर कोई असंतुलित बल कार्यरत नहीं है। अतः गेंद विरामावस्था में आने के लिए प्रयासरत है। (सही विकल्प का चयन करें) 
उत्तर:
(c) गेंद पर गति की दिशा के विपरीत एक बल कार्य कर रहा है।

प्रश्न 5. 
एक ट्रक विरामावस्था से किसी पहाड़ी से नीचे की ओर नियत त्वरण से लुढ़कना शुरू करता है। यह 20s में 400m की दूरी तय करता है। इसका त्वरण ज्ञात करें। अगर इसका द्रव्यमान 7 टन है तो इस पर लगने वाले बल की गणना करें। (1 टन = 1000 kg) 
उत्तर:
हल: दिया गया है-ट्रक विरामावस्था में है।
ट्रक का प्रारम्भिक वेग u = 0 m/s
तय की गई दूरी s = 400 m
त्वरण (a) = ?
समय (t) = 20s
द्रव्यमान m = 7 टन = 7 x 1000 kg = 7000 kg
गति के दूसरे समीकरण से  \(s=u t+\frac{1}{2} a t^{2}\)
मान रखने पर 
\(\begin{aligned} &400=0 \times 20+\frac{1}{2} \times a \times(20)^{2} \\ &400=0+\frac{1}{2} \times a \times 400 \end{aligned}\)
\(a=\frac{400}{200}\)
a = 2 मीटर / सेकण्डर²
अत: ट्रक का त्वरण (a) = 2 मीटर / सेकण्ड होगा।
∵ त्वरण (a) = 2 m/s²
द्रव्यमान (m) = 7000 kg
तब सूत्र F = m x a से
F = 7000 x 2  = 14,000 किग्रा. मीटर / सेकण्ड²
F = 14,000 न्यूटन
अतः ट्रक पर लगा बल (F) = 14,000 न्यूटन। 

प्रश्न 6. 
6.1 kg द्रव्यमान के एक पत्थर को 20 ms^-1 के वेग से झील की जमी हुई सतह पर फेंका जाता है। पत्थर 50m की दूरी तय करने के बाद रुक जाता है। पत्थर और बर्फ के बीच लगने वाले घर्षण बल की गणना करें। 
उत्तर:
हल: दिया गया है
पत्थर का द्रव्यमान (m) = 1 kg
पत्थर का प्रारंभिक वेग u = 20 m/s
तय की गई दूरी s = 50 m
अंतिम वेग v = 0
त्वरण (a) = ?
बल (F) = ?
गति के तीसरे समीकरण से,
v_² = u² + 2as
मान रखने पर
(0)² = (20)² + 2 x a x 50
0 = 400 + 100 a
या
-400 = 100a
a = 400/100 = -4 m/s²
a = -4 m/s²
ऋणात्मक चिह्न मंदन को प्रकट करता है।
अतः पत्थर का मंदन 4 मीटर / सेकण्ड² है।
अब सूत्र F = m x a से
बर्फ द्वारा पत्थर पर लगाया गया बल
F = (1 kg) x (-4 m/s)
= -4 kg m/s²
या
F = -4 न्यूटन
अत: बर्फ तथा पत्थर के बीच 4 न्यूटन (N) का घर्षण बल लगता है। 

प्रश्न 7. 
एक 8000 kg द्रव्यमान का रेल इंजन प्रति 2000 kg द्रव्यमान वाले पाँच डिब्बों को सीधी पटरी पर खींचता है। यदि इंजन 40000 N का बल आरोपित करता है तथा यदि पटरी 5000 N का घर्षण बल लगाती है, तो ज्ञात करें
(a) नेट त्वरण बल तथा 
(b) रेल का त्वरण। 
उत्तर:
हल: दिया गया है
(a) रेल इंजन का द्रव्यमान (m) = 8000 kg
डिब्बों की संख्या = 5
प्रत्येक डिब्बे का द्रव्यमान = 2000 kg
इंजन पर बल आरोपित है F = 40000 N
पटरी द्वारा लगाया गया घर्षण बल = 5000 N
चूँकि घर्षण बल एक अवरोधी बल है।
अतः रेलगाड़ी पर नेट त्वरण बल = इंजन का बल – पटरी द्वारा लगाया गया घर्षण बल
= 40,000 N - 5,000 N
 = 35,000 N
अतः रेलगाड़ी का नेट त्वरण बल 35,000 N होगा।

(b) 5 डिब्बों का कुल द्रव्यमान m = 5 x 2000
= 10,000 kg
जबकि डिब्बों पर नेट त्वरण बल F = 35,000 N
सूत्र F = ma से
रेल का त्वरण a =  \(\frac{\mathrm{F}}{m}=\frac{35,000 \mathrm{~N}}{10,000 \mathrm{~kg}}\)
अतः रेल का त्वरण a = 3.5 m/s² 

प्रश्न 8. 
एक गाड़ी का द्रव्यमान 1500 kg है। यदि गाड़ी को 1.7 ms^-2 के ऋणात्मक त्वरण (अवमंदन) के साथ विरामावस्था में लाना है, तो गाड़ी तथा सड़क के बीच लगने वाला बल कितना होगा? 
उत्तर:
हल: दिया गया है।
गाड़ी का द्रव्यमान (m) = 1,500 kg
त्वरण (मंदन) = -1.7 m/s²
माना कि गाड़ी व सड़क के बीच F बल लगता है, तब यही बल गाड़ी में मंदन उत्पन्न करेगा।
अतः सूत्र F = ma से
F = 1500 x (-1.7)
= -2550.0 N
F = -2,550 N
अतः बल मंदन के कारण गाडी की गति के विपरीत दिशा में लगेगा। 

प्रश्न 9.
किसी m द्रव्यमान की वस्तु जिसका वेग v है, का संवेग क्या होगा? 
(a) (mv)² 
(b) mv² 
(c) (1/2)mv²
(d) mv
(उपर्युक्त में से सही विकल्प चुनें।) 
उत्तर:
(d) mv

प्रश्न 10. 
हम एक लकड़ी के बक्से को 200 N बल लगाकर उसे नियत वेग से फर्श पर धकेलते हैं। बक्से पर लगने वाला घर्षण बल क्या होगा?
उत्तर:
चूँकि लकड़ी के बक्से को 200 N बल लगाकर उसे नियत वेग से फर्श पर धकेलते हैं, इसलिए उस पर लगने वाला घर्षण बल भी 200 N होगा।

प्रश्न 11. 
दो वस्तुएँ, प्रत्येक का द्रव्यमान 1.5 kg है, एक ही सीधी रेखा में एक - दूसरे के विपरीत दिशा में गति कर रही हैं। टकराने के पहले प्रत्येक का वेग 2.5 ms^-1 है। टकराने के बाद यदि दोनों एक - दूसरे से जुड़ जाती हैं, तब उनका सम्मिलित वेग क्या होगा? 
उत्तर:
हल: चूँकि यहाँ पर पहली वस्तु L.H.S. से R.H.S. की तरफ जा रही है इसलिए इसकी दिशा धनात्मक होगी। पहली वस्तु के लिए
m₁ = 1.5g
u₁ = + 2.5 m/s
दूसरी वस्तु R.H.S. से L.H.S. की तरफ जा रही है इसलिए उसकी दिशा ऋणात्मक होगी। दूसरी वस्तु के लिए
m₂ = 1.5 g
u₂ = -2.5 m/s
टक्कर से पहले दोनों वस्तुओं का कुल संवेग
= m₁u₁ + m₂u₂
= 1.5 x (+ 2.5) + (1.5) x (- 2.5)
= 1.5 x 2.5 - 1.5 x 2.5
= 3.75 - 3.75
= 0
माना दोनों वस्तुओं का टकराने के बाद का सम्मिलित वेग = v है।
तब टक्कर के बाद कुल संवेग = m₁v + m₂v
= (m₁ + m₂) v 
= (1.5 + 1.5)
= 3v kg m/s
संवेग संरक्षण के नियम के अनुसार टक्कर से पूर्व का कुल संवेग = टक्कर के बाद का कुल संवेग
\(v=\frac{0}{3}=0\)
v = = 0
वस्तुओं का सम्मिलित वेग = 0 m/s
अतः टक्कर के बाद दोनों वस्तुओं का सम्मिलित वेग शून्य होगा अर्थात् ये विरामावस्था में आ जायेंगी।

प्रश्न 12. 
गति के तृतीय नियम के अनुसार जब हम किसी वस्तु को धक्का देते हैं, तो वस्तु उतने ही बल के साथ हमें भी विपरीत दिशा में धक्का देती है। यदि वह वस्तु एक ट्रक है जो सड़क के किनारे खड़ा है, संभवतः हमारे द्वारा बल आरोपित करने पर भी गतिशील नहीं हो पाएगा। एक विद्यार्थी इसे सही साबित करते हुए कहता है कि दोनों बल विपरीत एवं बराबर हैं जो एक-दूसरे को निरस्त कर देते हैं। इस तर्क पर अपने विचार दें और बताएँ कि ट्रक गतिशील क्यों नहीं हो पाता?
उत्तर:
विद्यार्थी का तर्क गलत है। वस्तुतः क्रिया और प्रतिक्रिया बल विपरीत एवं बराबर होते हैं, परन्तु ये बल कभी भी एक ही वस्तु पर कार्य नहीं करते। जैसा कि उपर्युक्त उदाहरण में, हमारे द्वारा आरोपित बल ट्रक पर लगता है और ट्रक का प्रतिक्रिया बल हम पर लगता है। ट्रक के गतिशील होने का सम्बन्ध केवल ट्रक पर लगने वाले बल से होता है न कि हमारे द्वारा लगे बल से। अतः क्रिया-प्रतिक्रिया बल निरस्त नहीं हो पाते।

हमारे द्वारा ट्रक पर बल आरोपित किए जाने पर ट्रक गतिशील नहीं होता है, क्योंकि ट्रक का द्रव्यमान अधिक होता है, जिस कारण इसका जड़त्व भी अधिक होता है। अत्यधिक जड़त्व के कारण यह विराम अवस्था में होता है। ट्रक पर हमारे द्वारा लगाये गये बल के अतिरिक्त पृथ्वी द्वारा आरोपित घर्षण बल भी लगा होता है, जो हमारे द्वारा लगाये बल को संतुलित कर देता है। जिस कारण ट्रक गतिशील नहीं हो पाता है।

प्रश्न 13. 
200g द्रव्यमान की एक हॉकी की गेंद 10 m/s से गति कर रही है। यह एक हॉकी स्टिक से इस प्रकार टकराती है कि यह 5 m/s के वेग से अपने प्रारम्भिक मार्ग पर वापस लौटती है। हॉकी स्टिक द्वारा आरोपित बल द्वारा हॉकी की गेंद में आये संवेग परिवर्तन के परिमाप का परिकलन कीजिए।
उत्तर:
हल: दिया गया है-  m = 200g
\(=\frac{200}{100} \mathrm{~kg}=\frac{1}{5} \mathrm{~kg}\)
\(\begin{aligned} &u=10 \mathrm{~m} / \mathrm{s} \\ &v=5 \mathrm{~m} / \mathrm{s} \end{aligned}\)
संवेग में परिवर्तन  = mu - (-mv)
∴ दिशा विपरीत है  = mu + mv
u = 10 m/s v = 5 m/s
= m(u + v)
= 1/5 (10 + 5)
= 15/5 = 3 kg m/s.

प्रश्न 14.
10g द्रव्यमान की एक गोली सीधी रेखा में 150 ms^-1 के वेग से चलकर एक लकड़ी के टुकड़े के गुटके से टकराती है और 0.03s के बाद रुक जाती है। गोली लकड़ी को कितनी दूरी तक भेदेगी? लकड़ी के गुटके द्वारा गोली पर लगाए गए बल के परिमाण की गणना करें।
उत्तर:
हल: दिया गया हैद्रव्यमान (m) = 10g  \(=\frac{10}{1000} \mathrm{~kg}\)
= 0.01 kg
प्रारम्भिक वेग, u = 150 m/s
अंतिम वेग, v = 0 m/s
समय, t = 0.03
त्वरण की परिभाषा से, 
\(\begin{aligned} &a=\frac{v-u}{t} \\ &a=\frac{0-150}{0.03}=\frac{-15000}{3} \end{aligned}\)
 a = - 5000 m/s²
[ऋणात्मक चिह्न मंदन को प्रकट करता है]
अब गति के दूसरे समीकरण से
\(\begin{aligned} &s=u t+\frac{1}{2} a t^{2} \\ &s=150 \times(0.03)+\frac{1}{2} \times(-5000) \times(0.03)^{2} \end{aligned}\)
S = 4.5 – 2500 x 0.0009
= 4.5 – 2.2500
 s = 2.25 m
अतः गोली लकड़ी को 2.25 मीटर तक भेदेगी।
सूत्र F = ma
मान रखने पर F = 0.01 x (-5000)
F = -50 N
अतः लकड़ी द्वारा गोली पर लगाया गया बल F = 50 न्यूटन

प्रश्न 15. 
एक वस्तु जिसका द्रव्यमान 1kg है, 10 ms^-1 के वेग से एक सीधी रेखा में चलते हुए विरामावस्था में रखे 5kg द्रव्यमान के एक लकड़ी के गुटके से टकराती है। उसके बाद दोनों साथ - साथ उसी सीधी - रेखा में गति करते हैं। संघट्ट के पहले तथा बाद के कुल संवेगों की गणना करें। आपस में जुड़े हुए संयोजन के वेग की भी गणना करें। 
उत्तर:
हल: दिया गया है
वस्तु का द्रव्यमान (m₁) = 1kg
वस्तु का वेग, u₁ = 10 m/s
लकड़ी के टुकड़े का द्रव्यमान, m₂ = 5kg
लकड़ी के टुकड़े का वेग u₂ = 0 m/s (विरामावस्था में)
तब टकराने से पहले का कुल संवेग = m₁u₁ + m₂u₂
= 1 x 10 + 5 x 0
= 10 + 0 = 10 kg m/s
टकराने के बाद दोनों पिण्ड (m₁ + m₂) साथ - साथ उसी सीधी रेखा में वेग v से गति करते हैं।
 टकराने के बाद संयुक्त पिण्ड का संवेग
= (m₁ + m₂) v
= (1 + 5) v
= 6 v kg m/s
संवेग संरक्षण के नियमानुसार
टक्कर के पहले का कुल संवेग = टक्कर के बाद का कुल संवेग
अर्थात् 10 = 6v
या
\(\begin{aligned} &v=\frac{10}{6} \\ &v=\frac{5}{3}=1.67 \mathrm{~m} / \mathrm{s} \end{aligned}\)
अतः टक्कर के पहले तथा बाद में कुल संवेग = 10 किग्रा  मीटर / सेकण्ड
टक्कर के बाद संयुक्त पिण्ड का वेग = 1.67 मीटर / सेकण्ड

प्रश्न 16. 
100 kg द्रव्यमान की एक वस्तु का वेग समान त्वरण से चलते हुए 6s में 5 ms^-1 से 8 ms^-1 हो जाता है। वस्तु के पहले और बाद के संवेगों की गणना करें। उस बल के परिमाण की गणना करें जो उस वस्तु पर आरोपित है।
उत्तर:
हल: दिया गया है  m = 100 kg
u = 5 m/s
v = 8 m/s
t = 6s
वस्तु का प्रारंभिक संवेग, p = mu
= 100 x 5 = 500 kg m/s
तथा वस्तु का अंतिम संवेग, p = mv
= 100 x 8 = 800 kg m/s
अब
\(\begin{aligned} &\mathrm{F}=\frac{m v-m u}{t}=\frac{m(v-u)}{t} \\ &\mathrm{~F}=\frac{100 \times(8-5)}{6}=\frac{100 \times 3}{6} \\ &\mathrm{~F}=\frac{300}{6} \end{aligned}\)
F = 50 किग्रा. मीटर / सेकण्ड
या 
F = 50 न्यूटन
अतः वस्तु पर आरोपित बल का परिमाण = 50 N

प्रश्न 17. 
अख्तर, किरण और राहुल किसी राजमार्ग पर बहुत तीव्र गति से चलती हुई कार में सवार हैं, अचानक उड़ता हुआ कोई कीड़ा, गाड़ी के सामने के शीशे से आ टकराया और वह शीशे से चिपक गया। अख्तर और किरण इस स्थिति पर विवाद करते हैं। किरण का मानना है कि कीड़े के संवेग परिवर्तन का परिमाण कार के संवेग परिवर्तन के परिमाण की अपेक्षा बहुत अधिक है। (क्योंकि कीड़े के वेग में परिवर्तन का मान कार के वेग में परिवर्तन के मान से बहुत अधिक है।) अख्तर ने कहा कि चूँकि कार का वेग बहुत अधिक था अतः कार ने कीड़े पर बहुत अधिक बल लगाया जिसके कारण कीड़े की मौत हो गई। राहुल ने एक नया तर्क देते हुए कहा कि कार तथा कीड़ा दोनों पर समान बल लगा और दोनों के संवेग में बराबर परिवर्तन हुआ। इन विचारों पर अपनी प्रतिक्रिया दें।
उत्तर:
राहुल का उत्तर सही था चूँकि संवेग संरक्षण के नियम से टक्कर के समय किसी निकाय का कुल संवेग संरक्षित रहता है। इसलिए दोनों ही में एकसमान बल लगेगा तथा दोनों के संवेग में भी समान परिवर्तन होगा। लेकिन यहाँ पर कीड़े का द्रव्यमान कम है, इस कारण से इसके वेग में अधिक परिवर्तन होगा एवं कार का द्रव्यमान अधिक होने के कारण, उसके वेग में अपेक्षाकृत कम परिवर्तन होगा।

प्रश्न 18. 
एक 10kg द्रव्यमान की घंटी 80cm की ऊँचाई से फर्श पर गिरी। इस अवस्था में घंटी द्वारा फर्श पर स्थानांतरित संवेग के मान की गणना करें। परिकलन में सरलता हेतु नीचे की ओर दिष्ट त्वरण का मान 10ms^-2 लें।
उत्तर:
हल- घंटी का द्रव्यमान, m = 10 kg
प्रारम्भिक ऊँचाई अथवा दूरी, s = 80 cm
या
= \(\frac{80}{100}=\frac{4}{5} m\)
घंटी का त्वरण (a) = 10 m/s²
गिरते समय प्रारम्भिक वेग u = 0 m/s
माना फर्श पर पहुँचकर घंटी v वेग से फर्श से टकराती है।
तब गति के तीसरे समीकरण से, v² = u² + 2as
मान रखने पर,
\(v^{2}=(0)^{2}+2 \times 10 \times \frac{4}{5}\)
v² = 0 + 2 x 2 x 4 = 0 + 16
= 16 मीटर / सेकण्ड
∴ घंटी का वेग  \(v=\sqrt{16}\)
= 4 मीटर / सेकण्ड
अतः संवेग में परिवर्तन = m x v - mu
= 10 x 4 - 10 x 0
= 40 - 0 = 40 kg m/s 

अतिरिक्त अभ्यास प्रश्न:

प्रश्न 1. 
एक वस्तु की गति की अवस्था में दूरी - समय सारणी निम्नवत् है

समय ( सेकंड )	दूरी (मीटर)
0	0
1	1
2	8
3	27
4	64
5	125
6	216
7	343

(a) त्वरण के बारे में आप क्या निष्कर्ष निकाल सकते हैं? क्या यह नियत है ? बढ़ रहा है ? घट रहा है? या शून्य है?
(b) आप वस्तु पर लगने वाले बल के बारे में क्या निष्कर्ष निकाल सकते हैं? 
उत्तर:
हल: दी गई सारणी से वेग और त्वरण के मान प्रत्येक समय और दरी के लिए अलग - अलग ज्ञात करेंगे। 

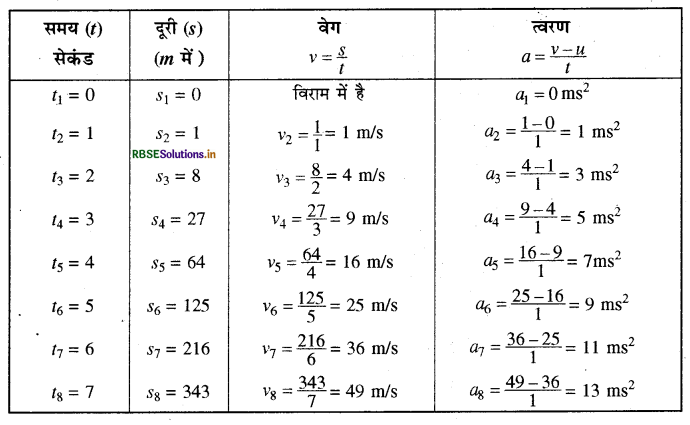
(a) चूँकि वस्तु का वेग प्रत्येक सेकण्ड में असमान रूप से बढ़ रहा है। यही कारण है कि वस्तु का त्वरण प्रत्येक सेकण्ड में बढ़ता जाता है जैसा कि ऊपरी सारणी में दिखाया गया है।

(b) यहाँ पर वस्तु का त्वरण बढ़ रहा है और बल जो कि द्रव्यमान और त्वरण के गुणनफल के बराबर होता है, अतः प्रति सेकण्ड वस्तु पर लगने वाला बल भी बढ़ रहा है।

प्रश्न 2. 
1200 kg द्रव्यमान की कार को एक समतल सड़क पर दो व्यक्ति समान वेग से धक्का देते हैं। उसी कार को तीन व्यक्तियों द्वारा धक्का देकर 0.2 ms^-2 का त्वरण उत्पन्न किया जाता है। कितने बल के साथ प्रत्येक व्यक्ति कार को धकेल पाते हैं। (मान लें कि सभी व्यक्ति समान पेशीय बल के साथ कार को धक्का देते हैं।)
उत्तर:
हल: स्थिति I :
दिया गया है
कार का द्रव्यमान m = 1200 kg
वेग  u = v (समान वेग से)
a = 0
बल = द्रव्यमान x त्वरण
F = m x a
= 1200 x 0 = 0 N
अतः प्रथम दो व्यक्तियों के धक्का देने का बल शून्य है।

स्थिति II: 
द्रव्यमान, m = 1200 kg
त्वरण, a = 0.2 m/s²
बल = m x a
= 1200 x 0.2
= 240 N.

प्रश्न 3. 
500g द्रव्यमान के एक हथौड़े द्वारा 50ms^-1 वेग से एक कील पर प्रहार किया जाता है। कील द्वारा हथौड़े को बहुत कम समय 0.01s में ही रोक दिया जाता है। कील के द्वारा हथौड़े पर लगाए गए बल का परिकलन करें। 
उत्तर:
हल: दिया गया है,
हथौड़े का द्रव्यमान, m = 500g
\(=\frac{500}{1000} \mathrm{~kg}=\frac{1}{2} \mathrm{~kg}\)
टकराते समय प्रारंभिक वेग, u = 50 m/s
अंतिम वेग, v = 0 m/s
समय, 1 = 0.01s
कील से टकराने पर हथौड़े का त्वरण
\(\begin{aligned} a &=\frac{v-u}{t} \\ &=\frac{0-50}{0.01}=-5,000 \\ a &=-5,000 \mathrm{~m} / \mathrm{s}^{2} \end{aligned}\)
ऋणात्मक चिह्न मंदन को प्रदर्शित करता है। . कील द्वारा हथौड़े पर लगाया गया बल
F = ma
\(F=\frac{1}{2} \times 5,000\)
F = 2,500 किग्रा मीटर / सेकण्ड
F = 2.500 न्यूटन

प्रश्न 4. 
एक 1200 kg द्रव्यमान की मोटरकार 90 km/h के वेग से एक सरल रेखा के अनुदिश चल रही है। उसका वेग बाहरी असंतुलित बल लगने के कारण 4s में घटकर 18 km/h हो जाता है। त्वरण और संवेग में परिवर्तन का परिकलन करें। लगने वाले बल के परिमाण का भी परिकलन करें। 
उत्तर:
दिया गया है,
द्रव्यमान (m) = 1200 kg
प्रारंभिक वेग (u) = 90 km/h
\(=90 \times \frac{5}{18} \mathrm{~m} / \mathrm{s}\)
= 25 m/s
अंतिम वेग (v) = 18 km/h = \(\frac{18 \times 5}{18} \mathrm{~m} / \mathrm{s}\)
= 5 m/s
t = 4s
त्वरण a = ?
संवेग में परिवर्तन = ?
बल F = ?
अतः कार का त्वरण 
\(\begin{aligned} &a=\frac{v-u}{t} \\ &a=\frac{5-25}{4} \\ &a=\frac{-20}{4} \end{aligned}\)
= - 5 मीटर / सेकण्ड²
ऋणात्मक चिह्न मंदन को प्रदर्शित करता है।
कार के संवेग में परिवर्तन = अंतिम संवेग – प्रारम्भिक संवेग
= mv - mu
या
m (v - u)
= 1200 (5 - 25)
= 1200 (- 20)
= – 24,000 किग्रा मीटर / सेकण्ड²
कार पर लगा बल F = ma
= 1200 x 5
= 6,000 न्यूटन
अतः कार का त्वरण = - 5 मीटर/सेकण्ड²
संवेग में परिवर्तन = 24,000 किग्रा मीटर/सेकण्ड की कमी
तथा कार पर लगा बल = 6,000 न्यूटन।