RBSE Class 9 Science Important Questions Chapter 8 Motion

Objective Type Questions

Question 1.
A particle is moving in a circular path of radius r. The displacement after half a circle would be :
(a) Zero
(b) πr
(c) 2r
(d) 2πr
Answer:
(c) 2r

Question 2.
A body is thrown vertically upward with velocity u, the greatest height h to which it will rise is :
(a) u/g
(b) u²/2g
(c) u²/g
(d) u/2g
Answer:
(b) u²/2g

Question 3.
The numerical ratio of displacement to distance for a moving object is :
(a) Always less than 1
(b) Always equal to 1
(c) Always more than 1
(d) Equal to or less than 1
Answer:
(d) Equal to or less than 1

Question 4.
If the displacement of an object is proportional to square of time, then the object moves with :
(a) Uniform velocity
(b) Uniform acceleration
(c) Increasing acceleration
(d) Decreasing acceleration
Answer:
(b) Uniform acceleration

Question 5.
From the given v - t graph figure, it can be inferred that the object is :

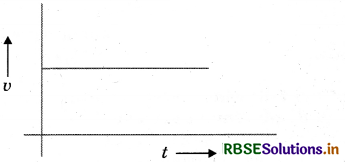
(a) In uniform motion
(b) At rest
(c) In non-uniform motion
(d) Moving with uniform acceleration
Answer:
(a) In uniform motion

Question 6.
Suppose a boy is enjoying a ride on a merry-go-round which is moving with a constant speed of 10 m s^-1. It implies that the boy is :
(a) At rest
(b) Moving with no acceleration
(c) In accelerated motion
(d) Moving with uniform velocity
Answer:
(c) In accelerated motion

Question 7.
Four cars A, B, C and D are moving on a levelled road. Their distance versus time graphs are shown in figure.

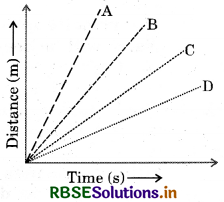
Choose the correct statement :
(a) Car A is faster than car D.
(b) Car B is the slowest.
(c) Car D is faster than car C.
(d) Car C is the slowest.
Answer:
(a) Car A is faster than car D.

Question 8.
Which of the following figure represents uniform motion of a moving object correctly?


Answer:

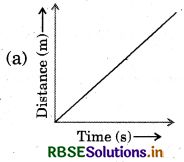
Question 9.
Area under a v - t graph represents a physical quantity which has the unit:
(a) m²
(b) m
(c) m³
(d) m s^-1
Answer:
(b) m

Question 10.
Slope of a velocity-time graph gives :
(a) distance
(b) displacement
(c) acceleration
(d) speed
Answer:
(c) acceleration

Question 11.
In which of the following cases of motions, the distance moved and the magnitude of displacement are equal?
(a) If the car is moving on straight road.
(b) If the car is moving in circular path.
(c) The pendulum is moving to and fro.
(d) The Earth is revolving around the Sun.
Answer:
(a) If the car is moving on straight road.

Question 12.
The rate of change in velocity is known as :
(a) force
(b) momentum
(c) acceleration
(d) distance
Answer:
(c) acceleration

Question 13.
If the graph of two quantities is a straight line then quantities are :
(a) constant
(b) equal
(c) proportional
(d) inversely proportional ‘
Answer:
(c) proportional

Question 14.
The velocity of a train changes from 20 m/s to 60 m/s in 10 seconds. Water will be acceleration of the train?
(a) 4 m/s²
(b) 12 m/s²
(c) 2 m/s²
(d) 6 m/s²
Answer:
(a) 4 m/s²

Question 15.
The instantaneous speed of an object can be measured by :
(a) Speedometer
(b) graph
(c) vector method
(d) None of these
Answer:
(a) Speedometer

Question 16.
Fill in the blanks :
(a) The shortest distance measured of an object from initial position to final position is known as ................
(b) We need a point to describe the location of an object, which is called ................ point.
(c) The motion of an object along a circular path around a fixed point with uniform speed is known as ................
(d) The area under the velocity-time graph gives the ................ covered in a given time interval.
(e) The graph between covered distance and time for uniform monitor is a ................
Answer:
(a) displacement
(b) reference
(c) uniform circular motion
(d) distance
(e) straight line

Question 17.
Match the column (A) with the column (B).

Column (A)	Column (B)
(1) Displacement	(a) Scalar quantity
(2) Speed	(b) Vector quantity
(3) Average velocity	(c) Same
(4) Unit of speed and velocity	(d) \(\frac{u+v}{2}\)
(5) v-t graph for uniformly accelerated motion	(e) Straight line

Answer:

Column (A)	Column (B)
(1) Displacement	(b) Vector quantity
(2) Speed	(a) Scalar quantity
(3) Average velocity	(d) \(\frac{u+v}{2}\)
(4) Unit of speed and velocity	(c) Same
(5) v-t graph for uniformly accelerated motion	(e) Straight line

Question 18.
Read the statements carefully and identify whether they are True or False-
1. Displacement and distance are always equal.
2. Area under velocity-time graph gives acceleration.
3. Distance-time graph is always a straight line for all types of motion.
4. If a vehicle is moving with a constant velocity, then its acceleration is constant.
5. In uniform circular motion, the velocity changes continuously.
Answer:
1. False
2. False
3. False
4. True
5. True

Very Short Answer Type Questions

Question 1.
Define the term velocity. What is its unit? Is it a scalar or vector quantity?
Answer:
Velocity is a physical quantity that gives the speed and direction of motion of the body.

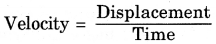
The SI unit of velocity is ms^-1. Velocity is a vector quantity because its description requires both magnitude and direction.

Question 2.
What is the relationship between distance travelled and the time elapsed for the motion with uniform velocity?
Answer:
Distance is directly proportional to time used.
In fact, distance travelled = Uniform velocity × Time used.

Question 3.
Define acceleration. Is it a scalar or a vector quantity?
Answer:
Acceleration is the measure of the change in the velocity of an object per unit time. It is seen in non-uniform motion. Acceleration is a vector quantity.

Question 4.
What is the SI unit of acceleration?
Answer:
The SI unit of acceleration is m/s².

Question 5.
What is the acceleration of a body moving uniform velocity?
Answer:
The acceleration of a body moving with uniform velocity is zero.

Question 6.
Differentiate acceleration from velocity.
Answer:
Velocity is the change in position of a body per unit time in a given direction and acceleration is the change in velocity of a body per unit time.

Question 7.
“The direction in which an object moves is given by the direction of velocity of the object and not the direction of acceleration.” Give an example to justify this statement.
Answer:
When an object is thrown upward, its velocity is directed upward while its acceleration is directed downwards. Thus, the velocity determines the direction of motion.

Question 8.
When is the acceleration of a body positive?
Answer:
The acceleration of a body is taken to be positive if it is in the direction of velocity.

Question 9.
Name the different types of graph.
Answer:
Bar graphs, straight line graphs, histograms, etc.

Question 10.
Which type of graph is used to describe motion?
Answer:
Line graph is used to describe the motion of an object.

Question 11.
Name the two types of physical quantities.
Answer:
The two types of physical quantities are scalar quantity and vector quantity.

Question 12.
What is magnitude?
Answer:
The numerical value of a physical quantity is called its magnitude.

Question 13.
Define a scalar quantity.
Answer:
A physical quantity which has only magnitude and no direction is called a scalar quantity.

Question 14.
Give two examples of a scalar quantity.
Answer:
Two examples of a scalar quantity are distance and speed.

Question 15.
Define vector quantity.
Answer:
A physical quantity which has both magnitude and direction is called a vector quantity.

Question 16.
Give the simplest type of motion.
Answer:
The simplest type of motion is the motion along a straight line.

Question 17.
Give two examples of a vector quantity.
Answer:
Two examples of a vector quantity are displacement and velocity.

Question 18.
When is the acceleration of a body is negative?
Answer:
The acceleration of a body is taken to be negative when it is opposite to the direction of velocity.

Question 19.
Define uniform acceleration. Give one example.
Answer:
Uniform acceleration: An object has a uniform acceleration if it travels in a straight line and its velocity increases or decreases by equal amounts in equal intervals of time.
For example: The motion of a freely falling body has uniform acceleration.

Question 20.
Define non-uniform acceleration. Give one example.
Answer:
Non-uniform acceleration: An object has non-uniform acceleration if it travels in a straight line and its velocity increases or decreases by unequal amounts in equal intervals of time.
For example: The movement of a car on a busy road has non-uniform acceleration.

Question 21.
How does the velocity change with time in uniform rectilinear motion of an object?
Answer:
In uniform rectilinear motion of an object, the velocity is constant with time, i.e. change in velocity of the object during any time interval is zero.

Question 22.
How does the velocity change with time in non-uniform rectilinear motion of an object?
Answer:
The velocity has different values at different instant of time and at different points of its path, i.e. change in velocity of the object during any time interval is not zero.

Question 23.
What do graphs provide?
Answer:
The graphs provide a convenient method to present pictorially the basic information about a variety of events such as motion.

Question 24.
Give an example of use of bar graph and straight graph.
Answer:
In telecast of one-day cricket match on T.V. vertical bar graphs show the run rate of a team in over.
Straight line graph helps in solving linear equation in two variables.

Question 25.
When do we say that the position of body has changed?
Answer:
If the distance or direction or both of a body relative to a reference point changes then we say that the position of the body has changed.

Question 26.
Which instrument is used to measure the distance covered by a vehicle?
Answer:
Odometer.

Question 27.
What can be determined using distance-time graph?
Answer:
Speed of an object.

Question 28.
What does the slope of a velocity-time graph represent?
Answer:
Acceleration.

Question 29.
Give two examples of non-uniform motion.
Answer:

1. Car moving on a road.
2. A person jogging in the park.

Question 30.
How many times an athlete has to change the direction of running to complete one round on a hexagonal path?
Answer:
Six times.

Question 31.
What is the S.I. unit of acceleration?
Answer:
m/s² or ms^-2.

Question 32.
In rainy season, raindrops fall-with uniform velocity or uniform acceleration?
Answer:
Uniform acceleration.

Question 33.
What does the speedometer of a bus measure, average speed or instantaneous speed?
Answer:
Instantaneous speed.

Question 34.
Does the value of instantaneous velocity and instantaneous speed always same?
Answer:
Yes.

Question 35.
What does the area covered under velocity-time graph represent?
Answer:
Displacement.

Question 36.
Can curve of displacement-time graph be perpendicular to its time axis?
Answer:
No, because the slope of curve cannot be infinity.

Short Answer Type Questions

Question 1.
Why is the motion in a circle at constant speed called accelerated motion?
Answer:
When a body moves along a circular path with a constant speed, its direction of motion at any point is along the tangent to the circle at that point, this motion called accelerated motion. The direction of motion changes as the body moves in a circle and causes a change in the velocity. Therefore, the motion of an object along a circular path is an accelerated motion.

Question 2.
A satellite revolves round the Earth with uniform speed. Is this motion accelerated? If so, in which direction does the acceleration act?
Answer:
The velocity of the satellite revolving around the Earth changes due to change in its direction of motion. So, the motion of satellite is an accelerated one. The acceleration is directed towards the centre of the Earth.

Question 3.
What is the difference between uniform linear motion and uniform circular motion?
Answer:

• When a body is moving with a uniform speed along a straight line, its motion is called linear uniform motion.
• The uniform linear motion is non accelerated motion.
• When a body is moving with a constant speed along a circular path, the direction of motion of body changes continuously with time.
• We know that a change in the direction of motion implies a change in velocity. Thus, uniform circular motion is an accelerated motion even though the speed of the body remains constant.

Question 4.
What is the meant by retardation? Give its SI unit.
Or
Give an example of negative acceleration.
Answer:
Retardation: When the velocity of a body decreases with time, its final velocity is less than the initial velocity, i.e. its acceleration is negative. This negative acceleration is called retardation. The SI unit of retardation is ms^-2.
Example: When brakes are applied to a moving car, its velocity gradually decreases. Under these conditions, the car is under retardation.

Question 5.
Classify the following as scalar and vector quantities :
Mass, weight, time, temperature, volume, velocity, speed, force, acceleration.
Answer:
Scalar quantity:
Mass, Time, Temperature, Volume, Speed

Vector quantity:
Weight, Velocity, Force, Acceleration

Question 6.
In a long distance race, the athletes were expected to take four rounds of the track such that the line of finish was same as the track was 200 m.
(i) What is the total distance to be covered by the athletes?
(ii) What is the displacement of the athletes when they touch the finish line?
(iii) Is the motion of the athletes uniform or non-uniform?
(iv) Is the distance moved by and displacement of athletes at the end of the race equal?
Answer:
(i) Total distance covered by the athletes = 4 × 200 = 800 m.
(ii) The line of start and the line of finish are the same so,
Displacement = 0
(iii) The motion of the athletes is non-uniform.
(iv) The distance and displacement of an athlete at the end of the race are not equal.

Question 7.
(i) Give an example of a body which may appear to be moving for one person and stationary for the other.
(ii) What can we tell about motion from the above example?
Answer:
(i) The man standing on the roadside observe that a bus along with its passenger is moving.
At the same time, a passenger sitting in the bus observes his fellow passenger to be at rest.
(ii) We can teU that motion is relative.

Question 8.
How many different binds of motion are there? Name them. Is there any motion which is a combination of two or more types of motion?
(i) There are three kinds of motion. These are:

• Linear or translatory motion.
• Circular or rotational motion.
• Vibratory or oscillatory motion

(ii) Complex motion means a combination of two or more types of motions.

Question 9.
What is motion? Give some examples of directly perceivable motion in daily life.
Answer:
(i) A body, is said to be in motion if it changes its position in relation to a reference point (origin).
(ii) Some examples of directly perceivable motion in daily life are:

• Birds and animals moving from one place to another.
• Cars moving on the roads.
• Aeroplanes flying in the sky.
• Blades of a moving fan.
• Fish swimming in water.

Question 10.
(i) Give an example of motion in human body which cannot be perceived directly.
(ii) Give an example of motion in nature which cannot be perceived directly.
(iii) Give an example of motion of the Earth which cannot be perceived directly.
Answer:
(i) The motion of blood through veins and arteries in human body cannot be perceived directly.
(ii) The motion of air is not perceived directly. We perceive it by observing the movement of dust or leaves of trees, etc.
(iii) The phenomena of sunrise, sunset and change of seasons is due to rotation and revolution of the Earth which can not be perceived directly.

Question 11.
Define the following:
(i) Translatory motion
(ii) Complex motion
Answer:
(i) When a body moves along a straight line, its motion is called rectilinear or translatory motion For example: A car moving on a straight road
(ii) When a body has two or more types of motion, it is said to possess complex motion For example : A ball rolling down on inclined planes has both rectilinear as well as circular motion

Question 12.
(i) Give some examples of erratic and uncontrolled motion.
(ii) Give an example of controlled motion which can be a service to human beings.
(iii) Is there a need to study about the erratic which of some objects and learn to control them?
Answer:
(i) Flooded river, a hurricane, a tsunami, etc.
(ii) Controlled motion of a river in a dam is useful to generate hydroelectric power.
(iii) Yes, we should study about the erratic motion of some objects because it will help us in disaster management.

Question 13.
Write the equations of motion.
Answer:
There are three equations of motion :
(i) v = u + at
(ii) s = ut + \(\frac{1}{2}\)at²
(iii) 2as = v² - u²

Question 14.
Define speed. How can we determine the value of average speed?
Answer:
The distance travelled by the body per unit time is the speed of a body. Its unit is m/s or ms^-1.
In most cases, objects make with non-uniform motion. So we describe the rate of motion of such objects in terms of their average speed.
The average speed of the body is the total distance travelled by the total time taken to cover this distance.

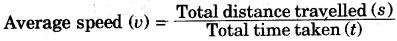
Long Answer Type Questions

Question 1.
From the study of velocity-time graph, what conclusion can be drawn for a particle moving in one-dimension? Explain.
Answer:
If velocity-time graph is a straight line parallel to time axis as shown in figure (a), then it shows the motion of constant velocity. In which the slope of velocity time is equal to the acceleration.

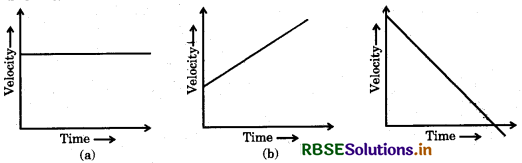
Figure (b) has positive slope which shows that the directions of acceleration and velocity are same. And velocity is increasing with the increase in time.
Figure (c) has negative slope which shows that velocity is decreasing. In this situation, the directions of acceleration and velocity are opposite.

The sum of different areas covered under the velocity-time graph between curve and time axis, is equal to the distance-covered by the particle, whereas algebraic sum of their areas is equal to the displacement.

Question 2.
How can we find the displacement using ν-t graph? Explain.
Answer:

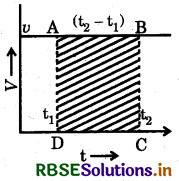
The area enclosed by velocity-time graph and time axis is equal to the magnitude of displacement in uniform motion. From graph, the area enclosed by rectangle is equal to the distance covered by particle.

The distance covered in the time interval (t₂ - t₁) is equal to the displacement. Since the motion is one-dimensional and direction is unchanged.
Therefore,
distance = velocity × time
s = AD × DC
S = ν (t₂ - t₁)
= Area of rectangle ABCD

Question 3.
Two stones are thrown vertically upwards simultaneously with their initial velocities u₁ and u₂ respectively. Prove that the heights reached by them would be in the ratio of u₁² : u₂² (assume upward acceleration is - g and downward acceleration to be + g).
Answer:
We know for upward motion, ν² = u² - 2gh
therefore, h = \(\frac{v^{2}-u^{2}}{2 g}\)
But at highest point v = 0
Therefore, h = \(\frac{u^{2}}{2 g}\)
For first ball, h₁ = \(\frac{u_{1}^{2}}{2 g}\)
For second ball, h₂ = \(\frac{u_{2}^{2}}{2 g}\)
Thus, \(\frac{h_{1}}{h_{2}}=\frac{u_{1}^{2} / 2 g}{u_{2}^{2} / 2 g}=\frac{u_{1}^{2}}{u_{2}^{2}}\)
or
h₁ : h₂ = \(u_{1}^{2}: u_{2}^{2}\)
Thus, proved.

Question 4.
Deduce the equations of motion for the uniformly accelerated one-dimensional motion.
Answer:
If a particle moving with velocity u changes to v in time t, then average acceleration will be
a = \(\frac{v-u}{t}\) .................(i)
or, v - u = at
or, v = u + at .............(ii)
It is the first equation of motion.
The average velocity of particle is = \(\frac{u+v}{2}\)
From equation (i), we have
average velocity = \(\frac{u+u+a t}{2}\)
= \(\frac{2 u+a t}{2}\)
= u + \(\frac{1}{2}\)at
∴ distance, s = average velocity × time
s = (u + \(\frac{1}{2}\)at) × t
or, s = ut + \(\frac{1}{2}\)at² .............(iii)
It is the second equation of motion,
From first equation of the motion,
ν = u + at
Taking squares of both the sides,
(ν)² = (u + at)²
ν² = u² + 2 uat + a²t²
= u² + 2a(ut + \(\frac{1}{2}\)at²)
ν² = u² + 2a s [from equation (iii)]
It is the third equation of motion.

Question 5.
Define uniform and non-uniform motion. Deduce the equation of motion with the help of velocity-time graph.
Answer:
Uniform motion : An object is said to be in uniform motion when it covers equal distance in equal time intervals.

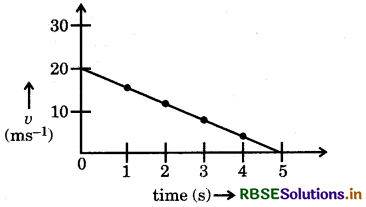
ν-t graph for an object moving with unifrom accelerated motion
Non-uniform motion : The motion is said to be non-uniform motion, when the body covers unequal distance in equal intervals of time.

ν-t graph for object moving with non-uniformly accelerated motion

Derivation of first equation of motion (velocity-time relation):
The rate of change in velocity is constant in uniform accelerated motion, therefore
\(\frac{1}{2}\) = a = constant
So the graph between velocity and time is a straight line, of which slope is equal to the acceleration.

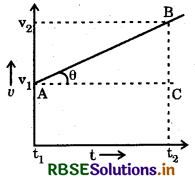
or, tanθ = a
from graph, \(\frac{B C}{C A}\) = tanθ = a
or, \(\frac{v_{2}-v_{1}}{t_{2}-t_{1}}\) = a
or, ν₂ - ν₁ = a (t₂ - t₁)
or, ν₂ = ν₁ + a (t₂ - t₁)
If t₁ = 0, ν₁ = u, t₂ = t and ν₂ = v
then ν = u + at ............(i)
This is the first equation of motion.

Derivation of second equation of motion (position-time relation) : Let us consider that the object has travelled a distance s in time t under uniform acceleration a. From graph, the distance travelled by the object is obtained by the area enclosed within OABC under the velocity-time graph AB.

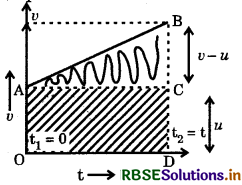
Thus, the distance s travelled by the object is given by
s = area of OABC trapezium
= area of rectangle OADC + area of triangle ABD
= OA × OC + \(\frac{1}{2}\) (AD × BD)
Substituting OA = u, OC = AD = t and BD = at,
We have s = ut + \(\frac{1}{2}\)(t × at)
s = ut + \(\frac{1}{2}\)at² ..............(ii)
This is the second equation of motion.

Derivation of third equation of motion (position-velocity relation) :
∵ s = ut + \(\frac{1}{2}\)at²
Substituting the value of t from equation (i),

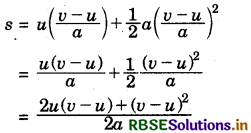
or, 2as = 2uv - 2a² + v² - 2uv + u²
or, 2as = v² - u² ..............(iii)

Question 6.
Obtain a relation for the distance travelled by an object moving with a uniform acceleration in the interval between 4th and 5th seconds.
(Hint : Use the equation of motion s = (ut + \(\frac{1}{2}\)at²)
Answer:
Distance travelled in 5 s,
s = u × 5 + \(\frac{1}{2}\) × a × (5)²
s = 5u + \(\frac{25}{2}\)a .........(i)
Similarly, distance travelled in 4 s,
s' = 4u + \(\frac{16}{2}\)a ........(ii)
Distance travelled in the interval between 4^th and 5^th seconds
=(s - s')= (u + \(\frac{9}{2}\)a)m

Question 7.
A bus covers s₁ distance with v₁ speed and s₂ distance with v₂ speed. What is the average speed of the bus? If distances are equal to each other then prove that the value of average speed will be \(\frac{2 v_{1} v_{2}}{v_{1}+v_{2}}\).
Answer:

Where t1 is the time to cover s1 distance and t2 is the time to cover s2 distance.

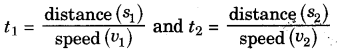
Hence, average speed \(v=\frac{s_{1}+s_{2}}{\left(\frac{s_{1}}{v_{1}}+\frac{s_{2}}{v_{2}}\right)}\)
If both distances are equal, i.e. s₁ = s₂, bus travels first half of its journey with v₁ speed and second half with v₂ speed,
thus, average speed = \(\frac{2 v_{1} v_{2}}{v_{1}+v_{2}}\)

Numerical Questions

Question 1.
A person moves along the boundary of a square field of side 10 m in 20 s. What will be the magnitude of displacement of that person at the end of 2 minutes 20 seconds?
Answer:
Side of square field = 10 m
So, perimeter = 10 m × 4 = 40 m
Person moves along the boundary in 20 sec.
Displacement after 2 m 20 sec = 2 × 60s + 20s = 140 s = ?
Since in 20 s person moves 40 m.
Therefore, in 1 sec distance covered = \(\frac{40}{20}\) = 2 m
Therefore, in 140 sec distance covered = 2 × 140 = 280 m
Now, number of rotation to cover 280 along the boundary =

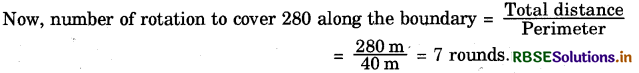
Hence, after 7 rounds the person will be at the starting point, so displacement will be zero.

Question 2.
Neha swims in a 90 m long pool. She covers 180 m in one minute by swimming from one end to the other and back along the same straight path. Find the average speed and average velocity of Neha.
Answer:
Total distance = 180 m
Total displacement = 0
Time taken t = 1 min = 60 s

Question 3.
The average speed of a bicycle, an athlete and car are 18 km/h, 7 m/s and 2 km/ min respectively. Which of the three is the fastest and which is the slowest?
Answer:

Thus, the average speeds of the bicycle, the athlete and the car are 5 m/s, 7 m/s and 33.3 m/s respectively. So, the car is the fastest and the bicycle is the slowest.

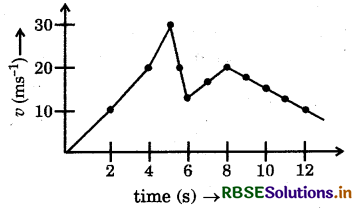
Question 4.
Figure represents the speed - time graph for a particle. Find the distance covered by the particle between t = 10 min and t = 30 min.

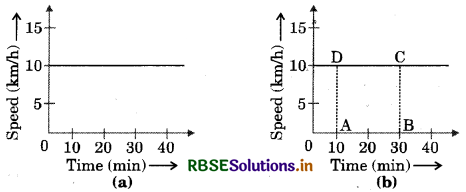
Answer:
We draw perpendicular lines from the 10-minute point and the 30-minute point to the time-axis (fig. b). The distance covered is equal to the area of the rectangle ABCD, its value is
ABCD = (30 min - 10 min) × (10 km/h)
= 20 min × 10 km/h
= \(\frac{20}{60}\)h × 10 km/h = \(\frac{10}{3}\)km

Question 5.
Find the distance covered by a particle during the time interval t = 0 to t = 20 s for which the speed-time graph is shown in figure.

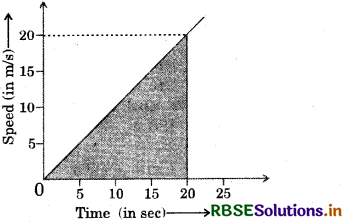
Answer:
The distance covered in the time interval 0 to 20 s is equal to the area of the shaded triangle. So,
Distance = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × (20 s) × (20 m/s) = 200 m.

Question 6.
A bus moves 30 km in 30 min and the next 30 km. in 40 min. Calculate the average speed for the entire journey.
Answer:
Given, the total time taken is 30 min + 40 min = 70 min and the total distance travelled is 30 km + 30 km = 60 km
The average speed is vav = \(\frac{60 \mathrm{~km}}{70 \mathrm{~min}}\) = \(\frac{60 \mathrm{~km}}{(70 / 60) \mathrm{h}}\) = \(\frac{3600}{70}\) km/hr = 51.4 km/h

Question 7.
A girl runs for 10 min at a uniform speed of 9 km/h. What should be the speed that she runs for the next 20 min, so that the average speed comes to 12 km/h?
Answer:
Total time = 10 min 20 min = 30 min
The average speed is 12 km/h using s = vt, the distance covered in 30 min is :
12 km/h × 30 min = \(\frac{12 \mathrm{~km}}{\mathrm{~h}}\) × \(\frac{1}{2}\)h = 6 km
The distance covered in the first 10 min is :
9 km/h × 10 min = \(\frac{9 \mathrm{~km}}{\mathrm{~h}}\) × \(\frac{1}{6}\)h = 1.5 km
Thus, he has to cover 6 km - 1.5 km = 4.5.km in the next 20 min.
The speed required is : \(\frac{4.5 \mathrm{~km}}{20 \mathrm{~min}}\) = \(\frac{4.5 \mathrm{~km}}{(20 / 60) \mathrm{h}}\) = 13.5 km/h.

Question 8.
It is estimated that the. radio signal takes 1.27 seconds to reach the Earth from the surface of the Moon. Calculate the distance of the Moon from the Earth. Speed of radio signal = 3 × 10s ms^-1 (speed of light in air).
Answer:
Here, time = 1.27 s
Speed = 3 × 10⁸ ms^-1
Distance = ?
Using distance = speed × time, we get
Distance = 3 × 10⁸ ms^-1 × 1.27 s
= 3.81 × 10⁸ m = 3.81 × 10⁵ km

Question 9.
A particle moves 3 m north, then 4 m east and finally 6 m south. Calculate the magnitude of displacement.
Answer:

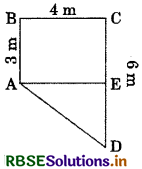
As shown in fig. let us consider east-west direction along x-axis and north-south direction along y-axis. Then AB, BC and CD represent the displacement of 3 m north, 4 m east and 6 m south respectively.
Obviously net displacement is represented by AB magnitude of net displacement s = AD
= \(\sqrt{(\mathrm{AE})^{2}+(\mathrm{ED})^{2}}\)
= \(\sqrt{(\mathrm{BC})^{2}+(\mathrm{CD}-\mathrm{AB})^{2}}\)
= \(\sqrt{(4)^{2}+(6-3)^{2}}\)
= \(\sqrt{(4)^{2}+(3)^{2}}\)
= \(\sqrt{16+9}\)
= \(\sqrt{25}\)
= 5m

Question 10.
A person moves a distance of 3 km towards east then 2 km towards north and then 3.5 km towards east. Find :
(a) the distance covered by the person, and
(b) the displacement of his motion.
Answer:

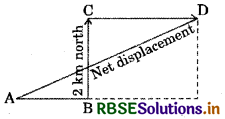
As shown AB, BC and CD represent the distance of 3 km east, 2 km north and 3.5 km east respectively.
(a) Net distance covered by a person = AB + BC + CD
= (3 + 2 + 3.5) km = 8.5 km
(b) Net displacement = AD = \(\sqrt{(\mathrm{AE})^{2}+(\mathrm{ED})^{2}}\)
= \(\sqrt{(\mathrm{AB}+\mathrm{CD})^{2}+(\mathrm{BC})^{2}}\)
= \(\sqrt{(3+3.5)^{2}+(2)^{2}}\)
= \(\sqrt{(6.5)^{2}+(2)^{2}}\)
= \(\sqrt{42.25+4}\)
= \(\sqrt{46.25}\)
= 6.8 km

Question 11.
An athlete completes one round of a circular track of diameter 49 m in 20 s. Calculate the distance covered and displacement at the end of 30 s.
Answer:
Here, diameter = 49 cm

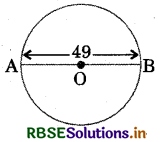
As an athlete completes one round of a circular track in a period T = 20 s, hence in time t = 30 s, he will complete n = [latex]\frac{30}{20}[/latex] = 1.5 rounds. Thus, he will beat point B diagonally opposite to initial position A
Displacement = AB = D = 49 m
Distance covered = n(2πr) = n(πD)
= 1.5 × \(\frac{22}{7}\) × 49 = 231 m

Question 12.
On a 120 km track, a train travels the first 30 km at uniform speed of 30 km/h. Calculate the speed with which the train should move rest of the track so as to get the average speed of 60 km/h for entire trip.
Answer:
As the average speed of a train for entire journey s = 120 km is v_av - 60 km/h
Hence, total time taken by train to cover the journey t = \(\frac{s}{v_{\mathrm{av}}}=\frac{120 \mathrm{~km}}{60 \mathrm{~km} / \mathrm{h}}\) = 2h
Time taken to travel first 30 km at uniform speed of 30 km/h
t₁ = \(\frac{30 \mathrm{~km}}{30 \mathrm{~km} / \mathrm{h}}\) = 1hr
Time for covering remaining distance [120 - 30] = 90 km should be
t₂ = t - t₁ = (2 - 1)h = 1 h
∴ Constant speed of train for this journey v₂
= \(\frac{s_{2}}{t_{2}}=\frac{90 \mathrm{~km}}{1 \mathrm{~h}}\) =90 km/h

Question 13.
A girl while riding a bicycle moves with the speed of 10 km/h for 2 hours and with the speed of 15 km/h in next 2 hours. Find the total distance moved by her and her average speed.
Answer:
Distance moved by girl in time (t₁) = 2h with a speed v₁ = 10 km/h is given as
s₁ = v₁t₁ = 10 × 2 = 20 km
and distance moved by girl in subsequent time t₂ = 3 h with speed v₂ = 15 km/h is given as :
s₂ = v₂t₂ = 15 × 3 = 45 km
Total distance moved by girl = 20 + 45 = 65
Her average speed for entire journey Vav

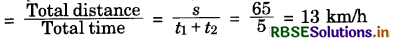
Question 14.
A cyclist completes 8 revolutions of a circular track of radius 98 m with a uniform speed in 40 minutes. Calculate the speed.
Answer:
Here no. of revolutions completed by the cyclist n = 8, radius of circular track r = 98 m and time, t = 40 min = 40 × 60 s = 2400 s

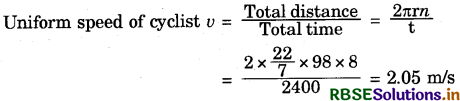
Question 15.
An object is dropped from rest at a height of 150 m and simultaneously another object is dropped from rest at a height of 100 m. What is the difference in their heights after 2 s if both the objects drop with same accelerations? How does the difference in heights vary with time?
Answer:
Initial difference in height, h = (150 - 100) m = 50 m
Both the objects are dropped simultaneously from rest (zero velocity),
Distance travelled by first object in 2 s = d₁ = ut + \(\frac{1}{2}\)at²
Initial speed = 0 (as the object was at rest), t = 2 s
Therefore, by substituting the values we get
= 0 + \(\frac{1}{2}\)g (2)² = 2 g = 2 × 9.8 = 19.6 m
Where, g = 9.8 m/s²
Distance travelled by another object in
2s = d² = 0 + \(\frac{1}{2}\)g (2)²
= 2 g = 19.6 m
After 2 s, height at which the first object will be h₁ = 150 - 19.6
After 2 s, height at which the second object will be h₂ = 100 - 19.6
Thus, after 2 s, difference in height = h₁ - h₂
= 150 - 19.6 - (100 - 19.6) = 50 m
After 2 s, the difference in height will be 50 m = Initial difference in height (h)
Thus, difference in height does not vary with time.

Question 16.
An object starting from rest travels 20 m in first 2 s and 160 m in next 4 s. What will be the velocity after 7 s from the start?
Answer:
Let’s acceleration of the body be ‘a’.
Therefore, in order to find the acceleration of the body, we use
s = ut + \(\frac{1}{2}\)at²
Where, u = 0, t = 2 s and s = 20 m, a = ?
Therefore, by substituting the values we get,
20 = 0 + \(\frac{1}{2}\) × a × (2)²
20 = \(\frac{1}{2}\) × 4a
a = 20 × \(\frac{2}{4}\) = 10m/s²
To find final velocity (v), we use
v = u + at
v = 0 + 10 × 7
v = 10 m/s

Question 17.
Using following data, draw time-displacement graph for a moving object:

Use this graph to find average velocity for first 4 s, for next 4 s and for last 6 s.
Answer:

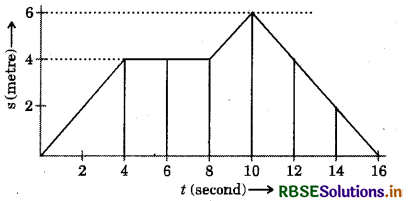
Average velocity for first 4s:

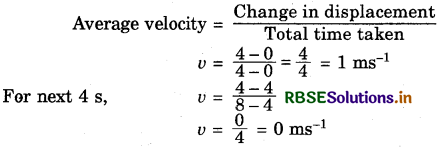
As s (metre) remains the same from 4 to 8 seconds, velocity is zero (refer the graph)
For last 6 s, v = \(\frac{0-6}{16-10}\) = -1 ms^-1

Question 18.
An electron moving with a velocity of 5 × 10⁴ m s^-1 enters into a uniform electric field and acquires a uniform acceleration of 10⁴ m s^-2 in the direction of its initial motion.
(i) Calculate the time in which the electron would acquire a velocity double of its initial velocity.
(ii) How much distance the electron would cover in this time?
Answer:
Given,
Initial velocity, u = 5 × 10⁴ ms^-1
and acceleration, a = 10⁴ m s^-2
(i) Final velocity = v = 2 u
v = 2 × (5 × 10⁴ ms^-1)
= 10 × 10⁴ m s^-1; t = ?
v = u + at or t = \(\frac{v-u}{a}\)
= \(\frac{\left(10 \times 10^{4}\right)-\left(5 \times 10^{4}\right)}{10^{4}}\)
= \(\frac{5 \times 10^{4}}{10^{4}}\)
= 5s

(ii) t = 5 s; a = 10⁴ m s^-2; u = 5 × 10⁴ m s^-1; s = ?
Now using the formula, s = ut + \(\frac{1}{2}\)at²
s = (5 × 10⁴) × 5 + \(\frac{1}{2}\)(10⁴) × (5)²
s = 25 × 10⁴ + \(\frac{25}{2}\) × (10⁴)
s = 25 × 10⁴ + 12.5 × (10⁴)
s = 37.5 × 10⁴ m