RBSE Solutions for Class 9 Science Chapter 8 गति

Rajasthan Board RBSE Solutions for Class 9 Science  Chapter 8 गति Textbook Exercise Questions and Answers.

RBSE Class 9 Science Solutions Chapter 8 गति

RBSE Class 9 Science Chapter 8 गति InText Questions and Answers

पृष्ठ 110.
 
प्रश्न 1. 
एक वस्तु के द्वारा कुछ दूरी तय की गई। क्या इसका विस्थापन शून्य हो सकता है? अगर हाँ, तो अपने उत्तर को उदाहरण के द्वारा समझाएँ।
उत्तर:
हाँ, इसका विस्थापन शून्य हो सकता है।

उदाहरण:
यदि कोई वस्तु एक वृत्ताकार पथ पर एक पूर्ण चक्कर के लिए गति करती है तो उसके लिए गति का प्रारम्भिक बिन्दु और अन्तिम बिन्दु एक ही प्राप्त होता है। इससे इसका विस्थापन शून्य होता है।

 

प्रश्न 2. 
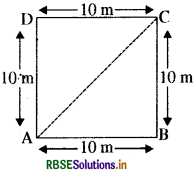
एक किसान 10m की भुजा वाले एक वर्गाकार खेत की सीमा पर 40s में चक्कर लगाता है। 2 मिनट 20 सेकण्ड के बाद किसान के विस्थापन का परिमाण क्या होगा? 
उत्तर:
हल: खेत की सीमा = AB + BC + CD + DA 
= 10 + 10 + 10 + 10
= 40 मीटर 

कुल समय = 2 मिनट 20 सेकण्ड
= 2 x 60 + 20
= 120 + 20 = 140 सेकण्ड 
प्रश्नानुसार, 40 सेकण्ड में तय की गई दूरी = 40 मीटर 
∴ 1 सेकण्ड में तय की गई दूरी = 1 मीटर
140 सेकण्ड में तय की गई दूरी = 1 x 140 = 140 मीटर 
यदि किसान मूल बिन्दु A से चलना प्रारम्भ करता है तो वह 140 मीटर की दूरी तय करने के बाद बिन्दु C पर होगा। 
अतः किसान का शुद्ध विस्थापन AC होगा। 
समकोण ∆ABC में
\(\begin{aligned} \mathrm{AC} &=\sqrt{(\mathrm{AB})^{2}+(\mathrm{BC})^{2}} \\ &=\sqrt{(10)^{2}+(10)^{2}}=\sqrt{100+100} \\ &=\sqrt{200}=\sqrt{100 \times 2} \\ &=10 \sqrt{2} \text { } \end{aligned}\)
या
= 10 x 1.414
= 14.14 मीटर 
अतः किसान के विस्थापन का परिणाम \(10 \sqrt{2}\)  मीटर या 14.14 मीटर है।

प्रश्न 3. 
विस्थापन के लिए निम्न में कौन सही है? 
(a) यह शून्य नहीं हो सकता है। 
(b) इसका परिमाण वस्तु के द्वारा तय की गई दूरी से अधिक है।
उत्तर:
(a) गलत 
(b) गलत

पृष्ठ 112.

प्रश्न 1. 
चाल एवं वेग में अंतर बताइए। 
उत्तर:
चाल एवं वेग में अन्तर:  

चाल	वेग
1. यह किसी भी दिशा में इकाई समय अन्तराल में तय की गई दूरी होती है।	1. यह एक निश्चित दिशा में किसी वस्तु के द्वारा इकाई समय अन्तराल में तय की गई दूरी है।
2. चाल एक अदिश राशि होती है जिसमें केवल परिमाण होता है।	2. यह एक सदिश राशि है जिसमें परिमाण के साथ - साथ दिशा का भी बोध होता है।
3. यह सदा धनात्मक होती है।	3. यह धनात्मक और ऋणात्मक दोनों हो सकता है।
4. गतिमान वस्तु की चाल शून्य नहीं होती है।	4. गतिमान वस्तु का वेग शून्य हो सकता है।
5. दूरी में परिवर्तन से चाल में परिवर्तन होता है।	5. वेग में परिवर्तन विस्थापन की मात्रा या दिशा परिवर्तन के कारण हो सकता है।

प्रश्न 2. 
किस अवस्था में किसी वस्तु के औसत वेग का परिमाण उसकी औसत चाल के बराबर होगा?
उत्तर:
यदि वस्तु द्वारा चली गई दूरी एवं विस्थापन का परिमाण एकसमान हो तो औसत वेग औसत चाल के बराबर होगा।

प्रश्न 3.
एक गाड़ी का ओडोमीटर क्या मापता है? 
उत्तर:
ओडोमीटर वाहनों द्वारा तय की गई दूरी को मापता है। 

प्रश्न 4. 
जब वस्तु एकसमान गति में होती है तब इसका मार्ग कैसा दिखाई पड़ता है? 
उत्तर:
जब वस्तु एकसमान गति में होती है तब वस्तु का पथ एक सरल रेखीय दिखाई पड़ता है।

प्रश्न 5. 
एक प्रयोग के दौरान, अंतरिक्षयान से एक सिग्नल को पृथ्वी पर पहुँचने में 5 मिनट का समय लगता है। पृथ्वी पर स्थित स्टेशन से उस अंतरिक्षयान की दूरी क्या है ? (सिग्नल की चाल = प्रकाश की चाल = 3 x 10⁸ms^-1)
उत्तर:
हल:
सिग्नल को पृथ्वी तक पहुँचाने में लगा समय = 5 मिनट 
अतः t = 5 x 60 = 300 सेकण्ड 
सिग्नल की चाल = 3 x 10⁸ m/s
दूरी (s) = चाल (v) x समय (t)
= 3 x 10⁸ x 300
= 9 x 10¹⁰ मीटर 

पृष्ठ 114.

प्रश्न 1. 
आप किसी वस्तु के बारे में कब कहेंगे कि।
(i) वह एकसमान त्वरण से गति में है? 
(ii) वह असमान त्वरण से गति में है?
उत्तर:

(i) यदि एक वस्तु सीधी रेखा में चलती है और इसका वेग समान समयांतराल में समान रूप से घटता या बढ़ता है, तो वस्तु का त्वरण 'एकसमान त्वरण' कहलाता है।
(ii) यदि किसी गतिमान वस्तु के वेग में परिवर्तन की दर समय के विभिन्न अंतरालों में भिन्न - भिन्न होती है तो वस्तु में उत्पन्न त्वरण असमान त्वरण कहलाता है।

प्रश्न 2. 
एक बस की गति 5s में 80 kmh^-1 से घटकर 60 kmh^-1 हो जाती है। बस का त्वरण ज्ञात कीजिए।
उत्तर:
हल:
दिया है - बस का प्रारंभिक वेग u = 80 किमी / घण्टा
u = 80 x \(\frac{5}{18}\) मीटर/सेकंड
= \(\frac{400}{18}\) मीटर/सेकंड
अंतिम वेग, v = 60 किमी / घण्टा 
\(=60 \times \frac{5}{18}=\frac{300}{18}\) मीटर / सेकंड [किमी. / घण्टा को मी. / से. में बदलने के लिए सीधा \(\frac{5}{18}\) से गुणा किया जा सकता है।]
त्वरण की परिभाषा से,
\(a=\frac{v-u}{t}=\frac{\frac{300}{18}-\frac{400}{18}}{5}\)
∵ t = 5 सेकण्ड दिया है।
\(\therefore a=-\frac{100}{18 \times 5}=\frac{-100}{90}\)

अत: बस का त्वरण (a)  \(=-\frac{10}{9}\)  मीटर / सेकण्ड²
यहाँ पर ऋणात्मक चिह्न मंदन को प्रकट कर रहा है।

प्रश्न 3. 
एक रेलगाड़ी स्टेशन से चलना प्रारंभ करती है और एकसमान त्वरण के साथ चलते हुए 10 मिनट में 40 kmh^-1 की चाल प्राप्त करती है। इसका त्वरण ज्ञात कीजिए। 
उत्तर:
हल:
दिया गया है।
प्रारंभिक वेग, u = 0
अंतिम वेग, v = 40 किमी / घण्टा
\(=\frac{40 \times 5}{18}=\frac{200}{18}\)  मीटर / सेकंड
\(=\frac{100}{9}\)  मीटर / सेकंड
t = 10 मिनट = 10 x 60 = 600 सेकंड
त्वरण की परिभाषा से, a = \(\frac{v-u}{t}\)
अत: रेलगाड़ी का त्वरण,
 \(a=\frac{\frac{100}{9}-0}{600}=\frac{100}{9 \times 600}\)
\(=\frac{1}{54}\) = 0.018 मीटर/सेकण्ड²

पृष्ठ 118.

प्रश्न 1. 
किसी वस्तु के एकसमान व असमान गति के लिए समय दूरी - ग्राफ की प्रकृति क्या होती है? 
उत्तर:
(1) समान गति के लिए: किसी वस्तु की एकसमान गति के लिए समय-दूरी ग्राफ एक सरल रेखा होती है।

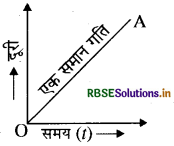
ग्राफ में OA भाग यह बतलाता है कि दूरी, समय के साथ एकसमान दर से बढ़ रही है।

(2) असमान गति के लिए: किसी वस्तु की असमान गति के लिए समय - दूरी ग्राफ एक वक्र रेखा में होता है।

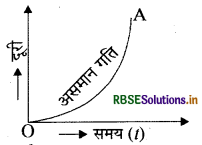
यहाँ पर ग्राफ OA असमान गति बतलाता है।
 

प्रश्न 2. 
किसी वस्तु की गति के विषय में आप क्या कह सकते हैं, जिसका दूरी - समय ग्राफ समय अक्ष के समानांतर एक सरल रेखा है?
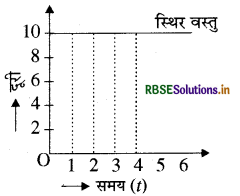
उत्तर:
दूरी: समय ग्राफ का समय अक्ष के समानान्तर एक सरल रेखां होना यह बताता है कि यह वस्तु विरामावस्था में है अर्थात् स्थिर है क्योंकि यह वस्तु समय के साथ स्थान में परिवर्तन नहीं कर रही है।

प्रश्न 3. 
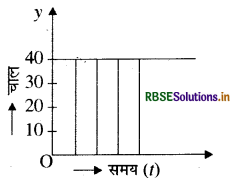
किसी वस्तु की गति के विषय में आप क्या कह सकते हैं, जिसका चाल - समय ग्राफ समय अक्ष के समानांतर एक सरल रेखा है?
उत्तर:
चाल: समय ग्राफ का समय अक्ष के समानान्तर एक सरल रेखा होना यह बताता है कि वस्तु की चाल स्थिर है, वह समय के साथ परिवर्तित नहीं हो रही है। अत: वस्तु एक समान चाल से गतिशील है।

प्रश्न 4. 
वेग - समय ग्राफ के नीचे के क्षेत्र से मापी गई राशि क्या होती है?
उत्तर:
यह क्षेत्रफल वस्तु द्वारा दिए गए समय अंतराल में कुल चली गई दूरी के बराबर होता है। 

पृष्ठ 121.

प्रश्न 1. 
कोई बस विरामावस्था से चलना प्रारंभ करती है तथा 2 मिनट तक 0.1 ms^-2 के एकसमान त्वरण से चलती है। परिकलन कीजिए
(a) प्राप्त की गई चाल तथा 
(b) तय की गई दूरी। 
उत्तर:
हल: दिया गया है, 
‘बस का प्रारंभिक वेग u = 0
त्वरण (a) = 0.1 मीटर / से.²
समय (t) = 2 मिनट
= 2 x 60 = 120 सेकंड 
अन्तिम वेग (v) = ?
तय की गई दूरी (s) = ?

(a) गति के प्रथम समीकरण से
v = u + at
y = 0 + 0.1 x 120
अतः प्राप्त की गई चाल = 12.0 = 12 मीटर / सेकण्ड

(b) गति के द्वितीय समीकरण से
\(\begin{aligned} s &=u t+\frac{1}{2} a t^{2} \\ s &=0 \times 120+\frac{1}{2} \times 0.1 \times(120)^{2} \\ &=0+\frac{1}{2} \times 0.1 \times 120 \times 120 \end{aligned}\)

अत: तय की गई दूरी = 720 मीटर. 

प्रश्न 2. 
कोई रेलगाड़ी 90 kmh-1 की चाल से चल रही है। ब्रेक लगाए जाने पर वह -0.5 ms^-2 का एकसमान त्वरण उत्पन्न करती है। रेलगाड़ी विरामावस्था में आने के पहले कितनी दूरी तय करेगी?
उत्तर:
हल-दिया गया है, रेलगाड़ी का प्रारंभिक वेग,
u = 90 किमी / घण्टा
u = 90 x 2 मी / से
u = 5 x 5 = 25 मी / से
त्वरण (a) = - 0.5 मी. / से²
अंतिम वेग (v) = 0
तय की गई दूरी (s) = ?
गति के तीसरे समीकरण से v² = u² + 2as
मान रखने पर (0) = (25) + 2 x (-0.5) x s
⇒ 0 = 625 - 1.0 s
⇒ s = 625 मीटर
अत: रेलगाड़ी विरामावस्था में आने से पहले 625 मीटर दूरी तय करेगी।

प्रश्न 3. 
एक ट्रॉली एक आनत तल पर 2 ms^-2 के त्वरण से नीचे जा रही है। गति प्रारंभ करने के 3s के पश्चात् उसका वेग क्या होगा?
उत्तर:
हल: दिया गया है,
ट्रॉली का प्रारंभिक वेग, u = 0
समान त्वरण, a = 2 मीटर / से.²
अन्तिम वेग, v = ?
समय, t = 3 सेकंड
गति के प्रथम समीकरण से, v = u + at
मान रखने पर, v = 0 + 2 x 3
y = 0 + 6 = 6 मीटर / सेकंड
अतः ट्रॉली का 3s बाद वेग 6 मीटर / सेकंड होगा।

प्रश्न 4.
एक रेसिंग कार का एकसमान त्वरण 4ms^-2 है। गति प्रारंभ करने के 10s पश्चात् वह कितनी दूरी तय करेगी?
उत्तर:
हल: दिया गया है,
त्वरण, a = 4 मीटर / सेकण्ड
प्रारम्भिक वेग, u = 0
समय, t = 10 सेकंड
दूरी, s = ?
गति के दूसरे समीकरण से,
\(s=u t+\frac{1}{2} a t^{2}\) 
मान रखने पर,
\(\begin{aligned} s &=0 \times 10+\frac{1}{2} \times 4 \times(10)^{2} \\ &=0+\frac{1}{2} \times 4 \times 10 \times 10 \end{aligned}\)
= 0 + 2 x 10 x 10 = 0 + 200
= 200 मीटर
s = 200 मीटर
अत: मति प्रारम्भ करने के 10 सेकण्ड पश्चात् वह 200 मीटर की दूरी तय करेगी।

प्रश्न 5. 
किसी पत्थर को ऊर्ध्वाधर ऊपर की ओर 5ms^-1 के वेग से फेंका जाता है। यदि गति के दौरान पत्थर का नीचे की ओर दिष्ट त्वरण 10ms^-2 है, तो पत्थर के द्वारा कितनी ऊँचाई प्राप्त की गई तथा उसे वहाँ पहुँचने में कितना समय लगा? 
उत्तर:
हल: दिया गया है,
u = 5 मीटर / से.
अन्तिम वेग, v = 0 (पत्थर की अधिकतम ऊँचाई पर वेग शून्य होगा)
त्वरण, a = -10 मीटर / से² (∴ त्वरण नीचे की ओर है, इसलिए ऋणात्मक लिया गया है।)
चलित दूरी, s = ?
समय, t = ?
गति के तीसरे समीकरण से
v² = u² + 2as
0 = (5)² + 2 x (- 10) x s
0 = 25 - 20s
20s = 25
∴ चलित दूरी s = 25/20 = 1.25 मीटर
अतः पत्थर के द्वारा प्राप्त की गई ऊँचाई = 1.25 मीटर
समय, \(t=\frac{v-u}{a}=\frac{0-5}{-10}=\frac{1}{2}\)
ऊँचाई प्राप्त करने में लगा समय t = 0.5 सेकंड

RBSE Class 9 Science Chapter 8 गति Textbook Questions and Answers

प्रश्न 1. 
एक एथलीट वृसीय रास्ते, जिसका व्यास 200m है, का एक चक्कर 40s में लगाता है। amin 20s के बाद यह कितनी दूरी तय करेगी और उसका बिस्थापन क्या होगा?
उत्तर:
दिया गया है,
वृत्त को ध्यास (Ar) = 200 मीटर
∴ त्रिज्या = \(\frac{200}{2}\) = 100 मीटर
समय = 40 सेकण्ड
वृत्ताकार रास्ते की परिधि = 2πr
= 2πr x 100 = 200π मीटर
एथलीट वृत्ताकार रास्ते पर कुल चलता है = 2 मिनट 20 सेकण्ड
अर्थात् = 2 x 60 + 20
= 120 + 20 = 140 सेकण्ड
∵ 40 सेकण्ड में एथलीट वृत्तीय रास्ते पर चलता है = 200π
∴ 1 सेकण्ड में चलेगा = \(\frac{200 \pi}{40}\) = 5π
∴ 140 सेकण्ड में चलेगा = 140 x 5π
= 700π मीटर
\(=700 \times \frac{22}{7}=2200\) मीटर
अतः 140 सेकंड में एथलीट 2200 मीटर चलेगा।

\(\begin{aligned} &=\frac{2200}{200 \pi} \\ &=\frac{2200 \times 7}{200 \times 22} \end{aligned}\)
= 3.5 चक्कर
3 चक्कर में विस्थापन का मान = शून्य
चूँकि प्रारम्भिक बिन्दु और अन्तिम बिन्दु एक ही हैं, अतः 0.5 चक्कर में विस्थापन = व्यास
= 200 मीटर
अतः एथलीट का विस्थापन 200 मीटर होगा।

प्रश्न 2. 
300m सीधे रास्ते पर जोसेफ जॉगिंग करता हुआ 2min 50s में एक सिरे A से दूसरे सिरे B पर पहुँचता है और घूमकर 1min. में 100m पीछे बिंदु C पर पहुँचता है। जोसेफ की औसत चाल और औसत वेग क्या होंगे?
(a) सिरे A से सिरे B तक तथा
(b) सिरे A से सिरे C तक। 
उत्तर:
A से B तक की दूरी
 AB = 300 मीटर

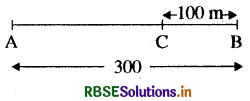
(a) सिरे A से सिरे B तक औसत चाल
कुल दूरी AB = 300 मीटर
कुल समय = 2 मिनट 50 सेकण्ड
= 2 x 60 सेकण्ड + 50 सेकण्ड
= 120 सेकण्ड + 50 सेकण्ड
= 170 सेकण्ड

\(=\frac{300}{170}=1.76\) मीटर / सेकण्ड
 पुन: विस्थापन = प्रारम्भिक बिन्दु A  से अन्तिम बिन्दु B  तक सीधे रास्ते दूरी 
AB =300 मीटर 
 लगा समय t = 170 सेकंड 

(b) सिरे A से सिरे C तक औसत चाल और वेग
कुल दूरी AB + BC = 300 + 100 = 400 मीटर
कुल लगा समय = 2 मिनट 50 सेकण्ड + 1.00 मिनट
= 3 मिनट 50 सेकण्ड
= 3 x 60 सेकण्ड + 50
सेकण्ड = 180 सेकण्ड + 50
सेकण्ड = 230 सेकण्ड

 = 1.74 मीटर / सेकण्ड

= 0.87 मीटर / सेकण्ड 

प्रश्न 3. 
अब्दुल गाड़ी से स्कूल जाने के क्रम में औसत चाल को 20 kmh^-1 पाता है। उसी रास्ते से लौटने के समय वहाँ भीड़ कम है और औसत चाल 40 kmh^-1 है। अब्दुल की इस पूरी यात्रा में उसकी औसत चाल क्या है?
उत्तर:
माना अब्दुल की आरम्भ बिन्दु और स्कूल के बीच की दूरी = x है। 
जाते समय औसत चाल = 20 km / h
माना जाने का समय = t₁ है।

माना वापस आते हुए समय लगता है = t₂
वापस आने की औसत चाल = 40 km / h

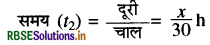
यात्रा का कुल समय = t₁ + t₂
\(=\frac{x}{20}+\frac{x}{40}=\frac{2 x+x}{40}=\frac{3 x}{40}\)
और कुल दूरी = x + x = 2x

\(=\frac{2 x}{\frac{3 x}{40}}\)

\(=\frac{2 x \times 40}{3 x}=\frac{80}{3}\)

= 26.66 km उत्तर 

प्रश्न 4. 
कोई मोटरबोट झील में विरामावस्था से सरल रेखीय पथ पर 3.0ms^-2 के नियत त्वरण से 8.0s तक चलती है। इस समय अंतराल में मोटरबोट कितनी दूरी तय करती है? 
उत्तर:
हल: दिया गया है, प्रारम्भिक वेग u = 0
त्वरण a = 3.0 m/s²
समय t = 8.0s
तय दूरी s = ?
गति के दूसरे समीकरण से,
\(s=u t+\frac{1}{2} a t^{2}\) 
मान रखने पर, 
\(\begin{aligned} s &=0 \times 8+\frac{1}{2} \times 3.0 \times(8.0)^{2} \\ &=0+\frac{1}{2} \times 3 \times 64=0+3 \times 32 \end{aligned}\)
= 0 + 96 = 96 m
अत: मोटरबोट द्वारा तय की गई दूरी = 96 मीटर

प्रश्न 5. 
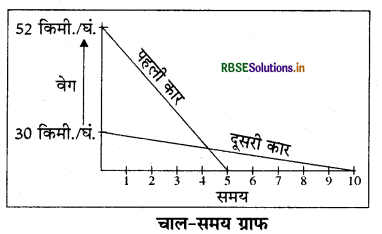
किसी गाड़ी का चालक 52 km/h^-1 की गति से चल रही कार में ब्रेक लगाता है तथा कार विपरीत दिशा में एकसमान दर से त्वरित होती है। कार 5 सेकण्ड में रुक जाती है। दूसरा चालक 30 km/h^-1 की गति से चलती हुई दूसरी कार पर धीमे - धीमे ब्रेक लगाता है तथा 10 सेकण्ड में रुक जाता है। एक ही ग्राफ पेपर पर दोनों कारों के लिए चाल - समय आलेखित करें। ब्रेक लगाने के पश्चात् दोनों में से कौन - सी कार अधिक दूर तक जाएगी? 
उत्तर:
पहली अवस्था में, कार का प्रारम्भिक वेग u = 52 km/h
\(\begin{aligned} &=52 \times \frac{5}{18} \mathrm{~m} / \mathrm{s} \\ &=\frac{130}{9} \mathrm{~m} / \mathrm{s} \end{aligned}\)
v= 0, t = 5 सेकण्ड

गति के प्रथम समीकरण से,
\(\begin{aligned} a=\frac{v-u}{t} &=\frac{\frac{0-130}{9}}{5}=\frac{\frac{-130}{9}}{5} \\ &=-\frac{130}{9 \times 5}=-\frac{26}{9} \mathrm{~m} / \mathrm{s}^{2} \end{aligned}\)
गति के दूसरे समीकरण से,
\(\begin{aligned} s &=u t+\frac{1}{2} a t^{2} \\ &=\frac{130}{9} \times 5+\frac{1}{2} \times \frac{26}{9} \times(5)^{2} \\ &=\frac{650}{9}+\frac{325}{9}=\frac{975}{9}=\frac{325}{3} \text { } \end{aligned}\)

दूसरी अवस्था में
कार का प्रारम्भिक वेग = 30 km
\(=\frac{30 \times 5}{18}=\frac{25}{3} \mathrm{~m} / \mathrm{s}\)

v = 0
समय t = 10 सेकण्ड
प्रश्नानुसार,  \(\begin{aligned} a &=\frac{v-u}{t}=\frac{0-\frac{25}{3}}{10} \\ &=\frac{-25}{3 \times 10}=\frac{-5}{3 \times 2}=\frac{-5}{6} \mathrm{~m} / \mathrm{s}^{2} \end{aligned}\)

दोनों कारों की दूरी का तुलनात्मक अध्ययन करने पर
\(\frac{375}{3} m, \frac{325}{3}\) से अधिक है।
अत: रुकने से पूर्व दूसरी कार अधिक दूरी तय करेगी।

प्रश्न 6.
चित्र में तीन वस्तुओं A, B और C के दूरी - समय ग्राफ प्रदर्शित हैं। ग्राफ का अध्ययन करके निम्न प्रश्नों के उत्तर दीजिए
(a) तीनों में से कौन सबसे तीव्र गति से गतिमान है?
(b) क्या ये तीनों किसी भी समय सड़क के एक ही बिंदु पर होंगे?
(c) जिस समय B, A से गुजरती है उस समय तक C कितनी दूरी तय कर लेती है?
(d) जिस समय B, C से गुजरती है उस समय तक यह कितनी दूरी तय कर लेती है?
उत्तर:

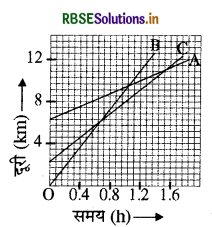
(a) B सबसे तेज गतिमान है चूँकि B समय अक्ष के साथ सबसे बड़ा कोण बनाता है, अर्थात् उस रेखा का ढाल A और C की अपेक्षा अधिक है।

(b) यदि तीनों व्यक्ति किसी विशेष समय में एक ही स्थान पर मिलते हैं, तो ये तीनों रेखाएँ किसी एक बिन्दु पर आकर मिलनी चाहिए। लेकिन ये तीन सीधी रेखाएँ किसी भी बिन्दु पर नहीं मिल सकतीं, अतः हम कह सकते हैं कि तीनों व्यक्ति एक ही बिन्दु पर समान रूप से कभी नहीं मिल सकेंगे।

(c) जब B तथा A एक-दूसरे को मिलते हैं, उस समय C मूल बिन्दु से लगभग 8 km. दूर है। चूंकि B तथा A जिस बिन्दु पर काटते या गुजरते हैं उस बिन्दु से सीधे लम्ब डालने पर वह C को काटता है जो कि मूल बिन्दु से लगभग 8 km दूर है।

(d) जहाँ B तथा C काटते या गुजरते हैं, वहाँ से y अक्ष पर लम्ब डालने पर मूल बिन्दु से लगभग 6 km दूरी है।

प्रश्न 7. 
20 मीटर की ऊँचाई से एक गेंद को गिराया जाता है। यदि उसका वेग 10 मीटर/से.²  के एकसमान त्वरण की दर से बढ़ता है तो यह किस वेग से धरातल से टकराएगी? कितने समय पश्चात् वह धरातल से टकराएगी? 
उत्तर:
दिया गया है, ऊँचाई (h) = 20 मीटर
u = 0 a = 10 m/s^-2
t = ?  v = ?
गति के तीसरे समीकरण से, \(v^{2}=u^{2}+2 a s\)
v² = (0)² + 2 x 10 x 20
v² = 400
^{\(v=\sqrt{400}\)}  = 20 मीटर/सेकण्ड
अत: गेंद धरातल से 20 मीटर/सेकंड के वेग से टकरायेगी।
गति के प्रथम समीकरण से,
v = u + at
20 = 0 + 10 x t
20 = 10t 
\(t=\frac{20}{10}\)
t = 2 सेकण्ड
अत: गेंद धरातल से 2 सेकंड बाद टकराएगी। 

प्रश्न 8. 
किसी कार का चाल-समय ग्राफ चित्र में दर्शाया गया है।

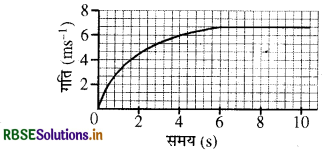
(a) पहले 4 सेकण्ड में कार कितनी दूरी तय करती है ? इस अवधि में कार द्वारा तय की गई दूरी को ग्राफ में छायांकित क्षेत्र द्वारा दर्शाइए।
(b) ग्राफ का कौन - सा भाग कार की एकसमान गति को दर्शाता है। 
उत्तर:
(a) पहले 4 सेकंड में कार 6 मीटर की दूरी तय करती है।

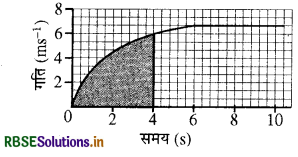
(b) प्रथम 6 सेकंड के बाद का ग्राफ एक सीधी रेखा है। अतः ग्राफ का यह भाग कार की एक समान गति को प्रदर्शित करता है।

प्रश्न 9.
निम्नलिखित में से कौन - सी अवस्थाएँ संभव हैं तथा प्रत्येक के लिए एक उदाहरण दें
(a) कोई वस्तु जिसका त्वरण नियत हो परन्तु वेग शून्य हो। 
(b) कोई त्वरित वस्तु एक समान चाल से गति कर रही हो। 
(c) कोई वस्तु किसी निश्चित दिशा में गति कर रही हो तथा त्वरण उसके लंबवत् हो।
उत्तर:
(a) यह स्थिति तभी सम्भव होती है जब किसी वस्तु को पृथ्वी तल से ऊपर की ओर फेंका जाता है तो अधिकतम ऊँचाई पर वस्तु का वेग शून्य होता है परन्तु त्वरण स्थिर (नियत) 9.8 m/s² या 10 m/s² ही रहता है।

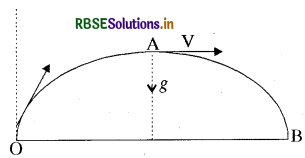
(b) यह असम्भव है, क्योंकि कोई भी वस्तु बिना चाल (वेग) परिवर्तन के त्वरित नहीं हो सकती है।

(c) यह असम्भव है, क्योंकि यदि त्वरण गति की दिशा के लम्बवत् होगा, तो दिशा निश्चित नहीं रह पायेगी, वह समय के साथ बदल जायेगी।
उदाहरण के लिए, जब हम किसी गेंद को छत से क्षैतिज दिशा में फेंकते हैं तो गेंद पर गुरुत्वीय त्वरण गति की दिशा के लम्ब दिशा में कार्य करता है, जिससे उसकी गति की दिशा बदलती जाती है।



प्रश्न 10. 
एक कृत्रिम उपग्रह 42250 km त्रिज्या की वृत्ताकार कक्षा में घूम रहा है। यदि वह 24 घंटे में पृथ्वी की एक परिक्रमा करता है तो उसकी चाल का परिकलन कीजिए।
उत्तर:
दिया गया है।
वृत्ताकार पथ की त्रिज्या (r) = 42,250 km 
एक चक्कर लगाने में लगा समय (1)= 24 
घंटे = 24 x 60 x 60 सेकण्ड 
∴ एक चक्कर में तय की गई दूरी = परिधि = 2πr
\(=2 \times \frac{22}{7} \times 42,250\)

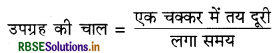
\(=2 \times \frac{22}{7} \times \frac{42250}{24 \times 60 \times 60}\)
 = 3.07 km/s