RBSE Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.9

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.9 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.9

प्रश्न 1.
एक लकड़ी के बुकशेल्फ (book-shelf) की बाहरी विमाएँ निम्न हैं. ऊँचाई = 110 cm, गहराई = 25 cm, चौड़ाई = 85 cm ( देखिए आकृति)। प्रत्येक स्थान पर तख्तों की मोटाई 5 cm है। इसके बाहरी फलकों पर पालिश कराई जानी है और आन्तरिक फलकों पर पेंट किया जाना है। यदि पालिश कराने की दर 20 पैसे प्रति cm है और पेंट कराने की दर 10 पैसे प्रति cm है, तो इस बुक-शैल्फ पर पालिश और पेंट कराने का कुल व्यय ज्ञात कीजिए।

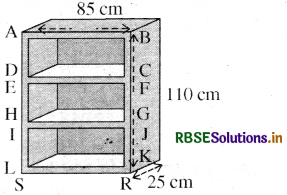
हल:
इस बुक-शैल्फ में प्रत्येक स्थान पर तख्तों की मोटाई 5 cm है।
∴ AB = 85 - 5 - 5 = 75 cm
तथा AD = [110 - 5 - 5 - 5 - 5]
= [110 - 20] cm
= 1 × 90
= 30 cm

पालिश होने योग्य बाहरी फलक = घनाभाकार बुक - शैल्फ के छः फलकों का क्षेत्रफल - 3 (खुले भाग ABCD का क्षेत्रफल)
= 2(110 × 25 + 25 × 85 + 85 × 110) - 3[75 × 30] cm
= 2[2750 + 2125 + 9350] - 3[2250] cm
= 2(14225) - 6750 cm
= 28450 - 6750 cm
= 21700 cm

लकड़ी के बुक-शैल्फ के बाहरी फलकों पर पालिश कराने का व्यय = 20 पैसे प्रति cm² = \(\frac{1}{5}\) रु. प्रति cm²
= (\(\frac{1}{5}\) × 21700) रु.
= 4340 रु.

क्योंकि यहाँ तीन बराबर भुजाओं वाले पाँच फलक हैं अतः कुल पृष्ठीय क्षेत्रफल
= 3[2(30 + 75) × 20 + 30 × 75] (∵ आन्तरिक गहराई = 25 - 5 = 20 cm)
= 3[2 × 105 × 20 + 2250]
= 3[4200 + 2250] = 3 × 6450
= 19350 रु.

अब आन्तरिक फलकों पर पेन्ट कराने का व्यय = 10 पैसे प्रति cm²
= 1 रु. प्रति cm = (10 × 19350) रु.
= 1935 रु. इस प्रकार पेन्ट कराने पर कुल व्यय
= 4340 रु. + 1935 रु.
= 6275 रु.

प्रश्न 2.
किसी घर के कम्पाउण्ड की सामने की दीवार को 21 cm व्यास वाले लकड़ी के गोलों को छोटे आधारों पर टिका कर सजाया जाता है, जैसा कि आकति में दिखाया गया है। इस प्रकार के आठ गोलों का प्रयोग इस कार्य के लिए किया जाना है और इन गोलों को चाँदी वाले रंग में पेंट करवाना है। प्रत्येक आधार 1.5 cm त्रिज्या और ऊँचाई 7 cm का एक

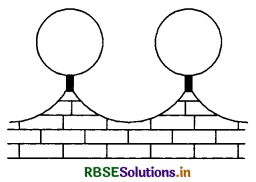
बेलन है तथा इन्हें काले रंग से पेंट करवाना है। यदि चाँदी के रंग का पेंट करवाने की दर 25 पैसे प्रति cm- है तथा काले रंग के पेंट करवाने की दर 5 पैसे प्रति cm- हो, तो पेंट करवाने का कुल व्यय ज्ञात कीजिए।
हल:
माना कि लकड़ी के गोलों की त्रिज्या R है
अतः व्यास (2R) = 21 cm
या R = 21 cm
इसी प्रकार माना कि बेलन के वृत्ताकार भाग की त्रिज्या r है। अत:
r = 1.5 cm

पेन्ट कराने योग्य गोले का पृष्ठीय क्षेत्रफल = गोले का पृष्ठीय क्षेत्रफल - बेलन के ऊपरी वृत्तीय भाग का क्षेत्रफल जिन पर गोले टिके हैं।

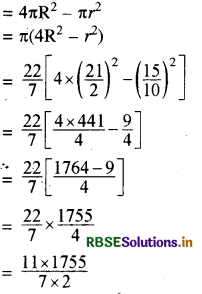
= 1378.928 cm²

ऐसे ही आठ गोलों का पृष्ठीय क्षेत्रफल
= 8x 1378.928 cm²
= 11031.424 cm

इस क्षेत्रफल पर चाँदी वाले रंग का पेन्ट कराने का व्यय
= (\(\frac{1}{4}\) × 11031.424) रु.
= 2757.85 रु.

अब बेलनाकार आधार का वक्रपृष्ठीय क्षेत्रफल
= 2πrh
= 2 × \(\frac{22}{7} \times \frac{15}{10}\) × 7
= 66 cm

ऐसे ही 8 बेलनाकार आधारों का पृष्ठीय क्षेत्रफल
= 8 × 66 cm
= 528 cm

इन पर काला पेन्ट कराने का व्यय
= (\(\frac{1}{20}\) × 528) रु.
= 26.4 रु.

इस प्रकार पेन्ट कराने का कुल व्यय
= 2757.85 रु. + 26.4 रु.
= 2784.25 रु.

प्रश्न 3.
एक गोले के व्यास में 25% की कमी हो जाती है। उसका वक्र पृष्ठीय क्षेत्रफल कितने प्रतिशत कम हो गया है?
हल:
माना कि गोले की त्रिज्या r है अत: व्यास d = 2r होगा।
या r = \(\frac{d}{2}\)
∴ गोले का पृष्ठीय क्षेत्रफल = 4πr²
= 4π\(\left(\frac{d}{2}\right)^{2}\)
= 4π.\(\frac{d^{2}}{4}\) = πd²

प्रश्नानुसार गोले के व्यास में कमी = 25% अर्थात्
= \(\frac{25}{100}\) × d = \(\frac{d}{4}\)
अब इस नए गोले का व्यास = d - \(\frac{d}{4}=\frac{3 d}{4}\)

माना इस नए गोले की त्रिज्या = r₁
व्यास (2r₁) = \(\frac{3 d}{4}\)
अब नए गोले का पृष्ठीय क्षेत्रफल = 4πr₁²
= 4π\(\left(\frac{3}{8} d\right)^{2}\)
= 4π\(\left(\frac{9}{64} d^{2}\right)=\frac{9 \pi}{16}\)d²

∴ वक्रपृष्ठ के क्षेत्रफल में परिवर्तन = मूल गोले का वक्रपृष्ठीय क्षेत्रफल - नए गोले का वक्रपृष्ठीय क्षेत्रफल
= πd² - \(\frac{9 \pi}{16}\)d²
= \(\frac{7}{16}\)πd²

∴ प्रतिशत परिवर्तन वक्र पृष्ठीय क्षेत्रफल में परिवर्तन