RBSE Solutions for Class 12 Physics Chapter 9 Ray Optics and Optical Instruments

Rajasthan Board RBSE Solutions for Class 12 Physics Chapter 9 Ray Optics and Optical Instruments Textbook Exercise Questions and Answers.

RBSE Class 12 Physics Solutions Chapter 9 Ray Optics and Optical Instruments

RBSE Class 12 Physics Ray Optics and Optical Instruments Textbook Questions and Answers

Question 9.1.
A small candle 2.5 cm in size is placed 27 cm in front of a concave mirror of radius of curvature 36 cm. At what distance from the mirror should a screen be placed in order to receive a sharp image? Describe the nature and size of the image. If the candle is moved closer to the mirror, how would the screen have to be moved?
Answer:
u = - 27 cm
R = - 36 cm
f = - 18 cm

The screen should be placed 54 cm from the mirror. The image is real, inverted and magnified.
m = \(\frac{\mathrm{I}}{\mathrm{O}}=\frac{v}{u}\)
\(\frac{1}{2.5}=\frac{54}{27}\)
∴ I = 5 cm
If the candle is moved closer, the screen would have moved farther and farther. Closer than 18 cm from the mirror, the image gets virtual and cannot be collected on the screen.

Question 9.2.
A 4.5 cm needle is placed 12 cm away from a convex mirror of focal length 15 cm. Give the location of the image and the magnification. Describe what happens as the needle is moved farther from the mirror?
Answer:
O = 4.5 cm
u = -12 cm, f = 15 cm

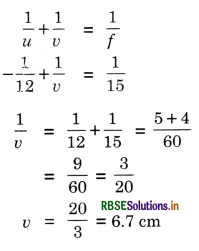
Image is virtual and erect and is formed behind the mirror

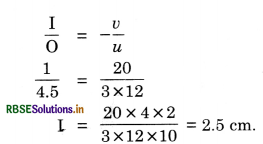
As the needle is moved farther from the mirror, the image moves towards the focus (but never beyond) and gets progressively diminished in size.

Question 9.3.
A tank is filled with water to a height of 12.5 cm. The apparent depth of a needle lying at the bottom of the tank is measured by a microscope to be 9.4 cm. What is the refractive index of water? If water is replaced by a liquid of refractive index 1.63 upto the same height, by what distance would the microscope have to be moved to focus on the needle again?
Answer:

= 7.7 cm nearly
Distance by which image becomes raised = 9.4 - 7.7 = 1.7 cm
The microscope will be moved up by 1.7 cm to focus on the needle again.

Question 9.4.
Fig. TBQ 9.4 (a) and (b) show refraction of a ray in air incident at 60° with the normal to glass in air and water-air interface respectively. Predict the angle of refraction in glass when the angle of incidence in water at 45° with the normal to a water-glass interface in Fig. TBQ 9.4 (c).

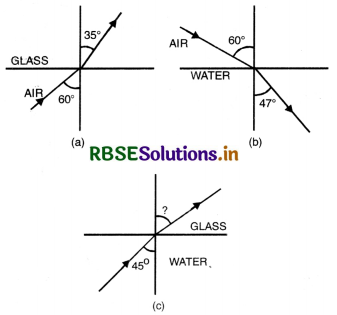
Answer:
First case,
Angle of incidence i = 60°
Angle of refraction r = 35°

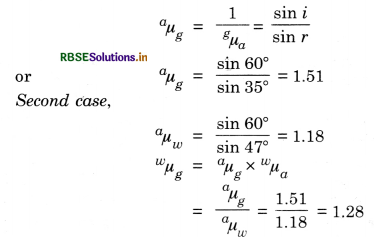
Third case,
Angle of incidence i = 45°
Angle of refraction r =?

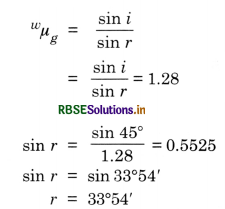
Question 9.5.
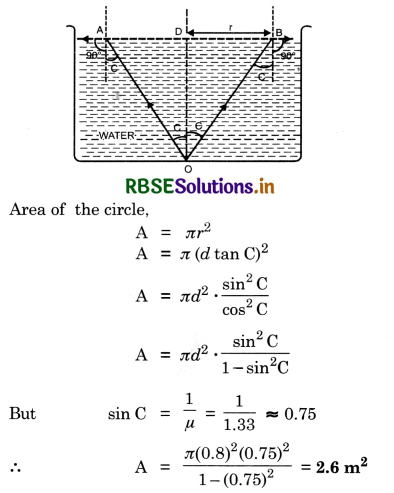
A small bulb is placed at the bottom of a tank containing water to a depth of 80 cm. Which is the area of the surface of water through which light from the bulb can emerge out? Refractive index of water is 1.33.
[Consider the bulb to be a point source]
Answer:
If r the radius (in m) of the large circle from which light comes out C is the critical angle for water-air interface, then
tan C = \(\frac{\mathrm{DB}}{\mathrm{DO}}=\frac{r}{d}\)
r = d tan C

Question 9.6.
A prism is made of glass of unknown refractive index. A parallel beam of light is incident on a face of the prism. The angle of minimum deviation of measured to be 40°. What is the refractive index of the material of the prism? The reflective angle of the prism is 60°. If the prism is placed in water (refractive index 1.33) predict the new angle of minimum deviation a parallel beam of light.
Answer:
µ = \(\frac{\sin \left(\frac{\mathrm{A}+\delta_m}{2}\right)}{\sin \left(\frac{\mathrm{A}}{2}\right)}\)
A = 60°, δ_m = 40°
µ = \(\frac{\sin 50^{\circ}}{\sin 30^{\circ}}\) = 2 x 0.766
= 1.532 ≈ 1.53
Now ^wµ_g = \(\frac{{ }^a \mu_g}{{ }^a \mu_w}=\frac{1.53}{1.33}\)
= 1.15
1.15 = \(\frac{\sin \left(\frac{60^{\circ}+\delta_m}{\sin 30^{\circ}}\right)}{\sin 30^{\circ}}\)
\(\sin \left(\frac{60^{\circ}+\delta_m}{2}\right)\) = 1.15 x sin 30°
\(\frac{60^{\circ}+\delta_m}{2}\) = 35.17°
δ_m = 10.34° = 10'20°

Question 9.7.
Double convex lenses are to be manufactured from a glass of refractive index 1.55, with both faces of the same radius of curvature. What is the radius of curvature required if the focal length of the lens is to be 20 cm?
Answer:
\(\frac{\mu_2}{\mu_1}\) = µ = 1.55
R₁ = R₁, R₂ = -R
f = 20

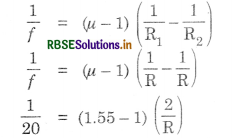
R = 0.55 x 2 x 20 = 22 cm

Question 9.8.
A beam of light converges at a point P. Now a lens is placed in the path of the convergent beam 12 cm from P. At what point does the beam converge if the lens is
(a) a convex lens of focal length 20 cm, and
(b) a concave lens of focal length 16 cm?

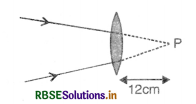
Answer:
Here the object is virtual and the image is real.
u = +12 cm (object on right and virtual)

(a) f = +20 cm

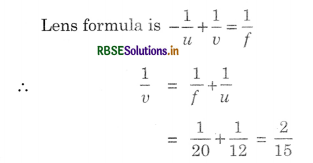
i.e, u = 7.5 cm (image on right and real.) It is located 7.5 cm from the lens.

(b) f = -16 cm

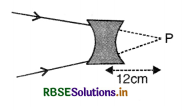
\(\frac{1}{v}=-\frac{1}{16}+\frac{1}{12}\)
i.e. v = 48 cm (image on right and real)
Image will be located 48 cm from the lens.

Question 9.9.
An object of size 3.0 cm is placed 14 cm in front of a concave lens of focal length 21 cm. Describe the image produced by the lens. What happens if the object is moved farther from the lens?
Answer:
o = 3.0 cm
u = -14 cm, f = -21 cm

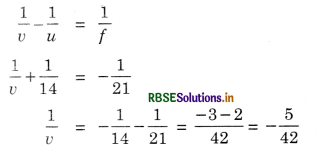
or v = -\(\frac{42}{5}\) = -8.4 cm
Image is erect, virtual and located 8.4 cm from the lens on the same side as the object. Using the relation,
\(\frac{\mathrm{I}}{\mathrm{O}}=\frac{v}{u}\)
v = \(\frac{8.4}{15}\) x 5 = 1.8 cm
As the object is moved away from the lens, the virtual image moves towards the focus of the lens and progressively diminishes in size. (When u = 21 cm, v = -10.5 cm and when u = ∝ , v = -21 cm.)

Question 9.10.
What is the focal length to a convex lens of focal length 30 cm in contact with a concave lens of focal length 20 cm? Is the system a converging or a diverging lens? Ignore the thickness of the lenses.
Answer:
Given f₁ = 30 cm, f₂ = - 20 cm, f = ?
Since f = \(\frac{f_1 f_2}{f_1+f_2}\)
∴ f = \(\frac{30 \times(-20)}{30-20}\)
or f = -60 cm.
Thus the system is a diverging lens of focal length 60 cm.

Question 9.11.
A compound microscope consists of an objective lens of focal length 2.0 cm and an eyepiece of focal length 6.25 cm separated by a distance of 15 cm. How far from the objective should an object be placed in order to obtain the final image at (a) the least distance of distinct vision (25 cm) and (b) at infinity? What is the magnifying power of the microscope in each case?
Answer:
(a) v_e = -25 cm
f_e = 6.25 cm
Using lens formula,
\(-\frac{1}{25}-\frac{1}{u_e}=\frac{1}{6.25}\)
\(\frac{1}{u_e}=-\frac{1}{25}-\frac{1}{6.25}\)
Now u_e = -5 cm
v₀ = 15 - 5 = 10 cm
f₀ = 2.0 cm

= 4 [1 + 4] = 20

(b) u₀ = -6.25 cm
v₀ = 15 - 6.25 = 8.75 cm
f₀ = 2.0 cm

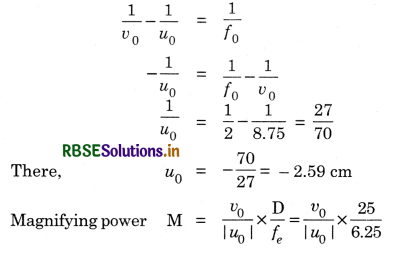
or M = \(\frac{8.75 \times 27}{8} \times \frac{25}{6.25}\) = 13.5 cm

Question 9.12.
A person with a normal near point (25 cm) using a compound microscope with objective of focal length 8.0 mm and eye piece of focal length 2.5 cm can bring an object placed 9.0 mm from the objective in sharp focus. What is the separation between the two lenses? Calculate the magnifying power of the microscope.
Answer:
Angular magnification of the eye piece for image at 25 cm
= \(\left(1+\frac{\mathrm{D}}{f}\right)=1+\frac{25}{2.5}\) = 11
For objective, u = -0.9 cm, f = 0.8 cm
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{v}=\frac{1}{0.8}-\frac{1}{0.9}=\frac{9-8}{7.2}=\frac{1}{7.2}\)
v = 7.2 cm
∴ Objective makes real image 7.2 cm from it on other side.
For eye piece, v = -25 cm, f₀ = 2.5 cm

∴ Eye piece lies ahead by 2.27 cm from the real image formed by the objective.
Distance between objective and eye piece
= 7.2 + 2.27 = 9.47 cm
Magnifying power of microscope
M = \(\frac{7.2}{0.9} \times \frac{-25}{-\frac{25}{11}}\) = 88

Question 9.13.
A small telescope has an objective lens of focal length 144 cm eyepiece of focal length 6.0 cm. What is the magnifying power of the telescope? What is the separation between the objective and the eye-piece?
Answer:
(a) For normal adjustment.
M.P. of telescope = \(\frac{f_0}{f_e}=\frac{144}{6}\) = 24

(b) The length of the telescope in normal adjustment
L = f₀ + f_e = 144 + 6
= 150 cm.

Question 9.14.
(a) A giant refracting telescope at an observatory has an objective lens of focal length 15 m. If an eyepiece of focal length 1.0 cm is used, what is the angular magnification of the telescope?
(b) If this telescope is used to view the moon, what is the diameter of the image of the moon formed by the objective lens? The diameter of the moon is 3.48 x 10⁶ m and the radius of lunar orbit is 3.8 x 10⁸.
Answer:
(a) Angular magnification
= \(\frac{f_0}{f_e}=\frac{15}{0.01}\) = 1500

(b) If d is the diameter of the image (in cm).
\(\frac{d}{1500}=\frac{3.48 \times 10^6}{3.8 \times 10^8}\)
i.e. d = 13.7

Question 9.15.
Use the mirror equation to deduce that:
(a) an object placed between f and 2f of a concave mirror produces a real image beyond 2f.
(b) a convex mirror always produces a virtual image independent of the location of the object.
(c) the virtual image produced by a convex mirror is always diminished in size and is located between the focus and the pole.
(d) an object placed between the pole and focus of a concave mirror produces a virtual and enlarged image.
Note. This exercise helps you to deduce algebraic properties of images that one obtains from explicit ray diagrams.
Answer:

and v = f (m + 1)

(a) When u > f < 2f, we get

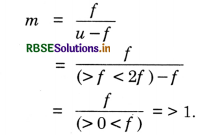
Hence v = f (m + 1) = f (>1 + 1)
or v > 2f
Since for concave mirror, f is negative, v becomes negative.
It means image is produced is real and beyond 2f.

(b) From mirror formula,
v = \(\frac{u f}{u-f}\)
Since for a convex mirror, f is positive and u is always negative, v will be always positive image will always be formed behind the mirror and will be virtual.

(c) From relation, m = \(\frac{f}{u-f} \) and f being, positive for convex mirror, m will always be negative and less than one. Hence virtual image formed will always be diminished.    
From relation, m = \(\frac{v-f}{f}\) and m being negative, v will always be less than f. Hence image will be formed between pole and focus.

(d) When u > 0 < f, we get
m = \(\frac{f}{u-f}=\frac{f}{(>0<f)-f}\)
= \(\frac{f}{(>-f<0)}\) = >-1
(∵ m is negative, image is virtual and enlarged because is numerical > 1).    

Question 9.16.
A small pin fixed on a tabletop is viewed from above from a distance of 50 cm. By what distance would the pin appear to be raised if it is viewed from the same point through a 15 cm thick glass slab held parallel to the table? Refractive index of glass = 1.5. Does the answer depend on the location of the slab?
Answer:
µ = 1.5; real thickness = 15 cm
µ = \(\frac{\text { Real Depth }}{\text { Apparent depth }}\)
1.5 = \(\frac{15}{\text { Apparent depth }}\)
∴ Apparent depth
= \(\frac{15}{1.5}\) = 10 cm
∴ Pin appears raised by 15 - 10 = 5 cm
The result is independent of the location of the slab.

Question 9.17.
(a) The figure TBQ 9.17 shows a cross-section a ‘light-pipe’ made of a glass fiber of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for which total reflections inside the pipe take place as shown in the figure?
(b) What is the answer if there is no outer covering of the pipe?

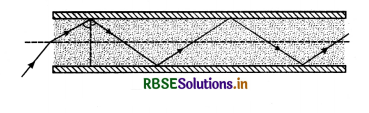
Answer:
(a) µ = \(\frac{1.68}{1.44}=\frac{1}{\sin \mathrm{C}}\)
or sin C = \(\frac{1.44}{1.68}\) = 0.8571
∴ C = 59°
Total internal reflection takes place when i > 59° or angle r may have values between 0 to 31°
∴ r_max = 31°
Now \(\frac{\sin i_{\max }}{\sin r_{\max }}\) =1.68
\(\frac{\sin i_{\max }}{\sin 31^{\circ}}\) = 1.68
sin i_max = 0.8652, i_max ≈ 60°
Thus all incident rays of angles in the range 0 < i < 60° will suffer total internal reflections in the pipe.

(b) If there is no outer coating pipe,
sin C = \(\frac{1}{\mu}\)
sin C = \(\frac{1}{1.68}\) = 0.5962
or sin C = sin 36.5°
or C = 36.5°
Now i = 90° will have r = 36.5° and i = 53.5° which is greater than C. Thus all incident rays (in the range 0 < i < 90°) will suffer internal reflections.

Question 9.18.
Answer the following questions:
(а) You have learned that plane and convex mirrors produce virtual images of objects. Can they produce real images under some circumstances? Explain.
(b) A virtual image, we always say, cannot be caught on a screen. Yet when we ‘see’ a virtual image, we are obviously bringing it onto the ‘screen’ (i.e. the retina) of our eye. Is there a contradiction?
(c) A diver under water, looks obliquely at a fisherman standing on the bank of a lake. Would the fisherman look taller or shorter to the diver than what he actually is?
(d) Does the apparent depth of a tank of water change if viewed obliquely? If so, does the apparent depth increase or decrease?
(e) The refractive index of diamond is much greater than that of ordinary glass, Is this fact of some use to a diamond cutter?
Answer:
(a) Rays converging to a point ‘behind’ a plane or convex mirror are reflected to a point in front of the mirror on the screen. In other words, a plane or convex mirror can produce a real image if the object is virtual.

(b) When the reflected or refracted rays are divergent, the image is virtual. The divergent rays can be converged onto a screen by means of an appropriate coverging lens. The convex lens of the eye does just that. The virtual image here serves as a (virtual) object for the lens to produce a real image. The screen here is not located at the position of the virtual image. There is no contradiction

(c) The rays starting from the head of the fisherman and incident on water become bent towards normal and appear to come from a higher point.
AF is real height of fisherman. Rays starting from A, bend towards normal. For divers they appear to come from A₁, A₁ F becomes apparent height of fisherman, which is more than real height.

(d) The apparent depth for oblique viewing decreases from its value for near-normal viewing.

(e) Refractive index of diamond is about 2.42, much larger than that of ordinary glass (about 1.5). The critical angle for diamond is above 24°, much less than that of glass. A skilled diamond cutter exploits the large range of angles of incidence (in the diamond), 24° to 90° to ensure that light entering the diamond is totally reflected from many faces before getting out thus producing a sparkling effect.

Question 9.19.
The image of a small electric bulb fixed on the wall of a room is to be obtained on the opposite wall 3 m away by means of a large convex lens. What is the maximum possible focal length of the lens required for the purpose?
Answer:
Let, v = +v ∴ u = -(3 - v), f_max = ?

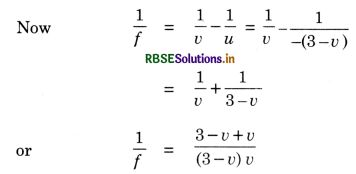
or 3v - v² = 3f
For f to be maximum d(f) = 0
i.e., d(3v - v²) = 0
i.e. 3 - 2v = 0
v = \(\frac{3}{2}\) = 1.5 m
Hence, u = -(3 - 1.5) = -1.5 m

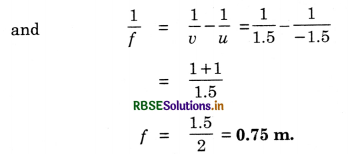
Question 9.20.
A screen is placed 90 cm from an object. The image of the object on the screen is formed by a convex lens at two different locations separated by 20 cm. Determine the focal length of the lens.
Answer:
Distance between object and image
D = 90 cm = u + v
Distance between two positions of lens
d = 20 = u - v
∴ u = 55 cm and v = 35 cm
From lens formula,
\(\frac{1}{f}=\frac{1}{55}+\frac{1}{35}=\frac{18}{385}\)
f = \(\frac{385}{18}\) = 21.4

Question 9.21.
(a) Determine the ‘effective focal length of the combination of the two lenses in Exercise 9.10 if they are placed 8.0 cm apart with their principal axes coincident. Does the answer depend on which side of the combination a beam of parallel light is incident? Is the notion of effective focal length of the system useful at all?
(b) An object 1.5 cm in size is placed on the side of the convex lens in the arrangement (a) above. The distance between the object and convex lens is 40 cm. Determine the magnification produced by the two-lens system and the size of the image.
Answer:
(a) (i) Let a parallel beam be incident from the left on the convex lens first.
f₁ = 30 cm, u₁ = -∞
Applying the formula, we have
\(\frac{1}{v_1}-\frac{1}{u_1}=\frac{1}{f_1}\)
\(\frac{1}{v_1}-\frac{1}{\infty}=\frac{1}{30}\)
v₁ = 30 cm (∵\(\frac{1}{\infty}\) = 0)
The image becomes a virtual object for the lens. Again
f₂ = -20 cm
u₂ = + (30 - 8) = +22 cm.
Therefore, \(\frac{1}{v_2}=-\frac{1}{20}+\frac{1}{22}\)
which gives v₂ = -220 cm.
The parallel incident beam appears to diverge from a point 220 - 4 = 216 cm from the center of the two-lens system.

(ii) Let the parallel beam be incident from the left on the concave lens first:
f₁ = -20 cm, u₁ = -∞
gives v₁ = - 20 cm. This image becomes a real object for the second lens:
f₂ = +30 cm,
u₂ = - (20 + 8) = - 28 cm.
Therefore, \(\frac{1}{v_2}=\frac{1}{30}-\frac{1}{28}\)
i.e. v₂ = -420 cm
The parallel incident beam appears to diverge from a point (420 - 416) cm on the left of the center of the two-lens system.
Clearly, the answer depends on which side of the lens system the parallel beam is incident. Further, we do not have a simple lens equation true for all u (and v) in terms of a definite constant of the system (the constant being determined by L and f₂ and the separation between the lenses). The notion of effective focal length, therefore, does not seem to be meaningful for this system.

(b) u₁ = - 40 cm, f₂ = 30 cm
For a lens, \(\frac{1}{v_1}+\frac{1}{u_1}=\frac{1}{f_1}\)
\(\frac{1}{v_1}+\frac{1}{40}=\frac{1}{30}\)
i.e. v₁ = 120
Magnitude of magnification due to the first (convex) lens = \(\frac{120}{40}\) = 3,
u = + (120 - 8)
=    +112 cm (object virtual);
f₂ = - 20 cm which gives
\(\frac{1}{\mathrm{v}_2}=-\frac{1}{20}+\frac{1}{112}\)
i.e. v₂ = \(\left(-\frac{112 \times 20}{92} \mathrm{~cm}\right)\)
Magnitude of magnification due to the second (concave) lens
= \(\frac{112 \times 20}{90 \times 112}=\frac{20}{92}\)
Net magnitude of magnification = \(\frac{3 \times 20}{92}\) = 0.98 cm.

Question 9.22.
At what angle should a ray of light be incident on the face of prism of refracting angle 60° so that it just suffers total internal reflection at the other face? The refractive index of the prism is 1.524.
Answer:
µ = \(\frac{1}{\sin C}\)
sin C = \(\frac{1}{\mu}=\frac{1}{1.524}\)
sin C = 0.6561 = sin 41°
C = 41°
A = r₁ + r₂
A = r + C
r = A - C
r = 60° - C = 60° - 41°
= 19°
\(\frac{\sin i}{\sin r}\) = 1.524
sin i = sin 19° x 1.524
= sin 29.7°
i = 29.7° ≈ 30°

Question 9.23.
You are given prisms made of crown glass and flint glass with a wide variety of angles. Suggest a combination of prisms that will
(а) deviate a pencil of white light without much dispersion.
(b) disperse (and displace) a pencil of white light without much deviation.
Answer:
Two identical prisms made of the same material placed with their bases on opposite sides (of the incident white light) and faces touching (or parallel) will neither deviate nor disperse, but will merely produce a parallel displacement of the beam.

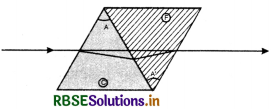
To deviate without dispersion, choose say the first prism to be of the crown glass, and take second prism a flint of suitably chosen refracting angle (smaller than that of crown glass prism because the flint prism disperses more) so that dispersion due to the first is nullified by the second.
For crown glass prism
Mean deviation, δ = (µ - 1)A
For Flint glass prism
δ' = (µ'- 1) A
Angular dispersion,
δ_v - δ_r = (µ_v - µ_r) A
And δ_v' - δ_r' = (µ'_v - µ'_r) A
For no dispersion
δ_v - δ_r = δ_v' - δ_r'
∴ (µ_v - µ_r) A = (µ_v' - µ_r') A
\(\left(\frac{\mu_v-\mu_r}{\mu-1}\right)\) (µ - 1) A = \(\left(\frac{\mu_v^{\prime}-\mu_r^{\prime}}{\mu^{\prime}-1}\right)\) (µ' - 1) A'
ω.δ = ω'δ'.
∴ \(\frac{\omega}{w^{\prime}}=\frac{\delta^{\prime}}{\delta}\)
It is the required condition.
For no deviation
δ = δ'
(µ - 1) A = (µ' - 1) A'
A' = \(\frac{(\mu-1)}{\left(\mu^{\prime}-1\right)}\) A
This is the required condition.

(b) To disperse without deviation, increase the angle of the flint glass prism so that deviations due to the two prisms are equal and opposite. (The flint glass prism angle will still be smaller than that of crown glass because flint glass has higher refractive index than that of crown glass). Because of the adjustments involved for so many colors, these are not meant to be precise arrangements for the purposes required.

Question 9.24.
For a normal eye, the far point is at infinity and the near point of distinct vision is about 25 cm in front of the eye. The corner of the eye provides a converging power of about 40 dioptres, and the least converging power of the eye lens behind the cornea is about 20 dioptres. From this rough data estimate the range of accommodation (i.e. the range of converging power of the eye lens) of a normal eye.
Answer:
To see objects at infinity, the eye uses its least converging power = (40 + 20) dioptres = 60 dioptres. This gives a rough idea of the distance between the retina and cornea-eye lens.
So focal length,
f = \(\frac{1}{\mathrm{P}}\)
or f = \(\frac{1}{60}\) m = \(\frac{5}{3}\) cm.
To focus an object at the near point (u = -25 cm), and the retina (v = 5/3 cm.) the focal length should be

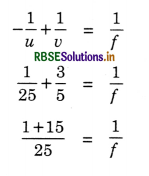
or f = \(\frac{25}{16}\) cm
∴ Converging power = \(\frac{1}{f}=\frac{1600}{25}\) = 64 D
∴ Power of the eye lens = 64 - 40 = 24 D
∴ The range of accommodation of the eye lens is roughly 20 to 24 D.

Question 9.25.
Does short-sightedness (myopia) or long-sightedness (hypermetropia) imply necessarily that the eye has partially lost its ability of accommodate? If not, what might cause these defects of vision?
Answer:
No, a person may have normal ability of accommodation of the eye lens and yet may be myopic or hypermetropic. Myopia arises when the eyeball from front to back gets too short. In practice, in addition, the eye lens may also lose some of its ability of accommodation. When the eyeball has the normal length but the eye lens loses partially its ability of accommodation (as happens with increasing age for any normal eye) the ‘defect’ is called presbyopia and is corrected in the same manner as hypermetropia.

Question 9.26.
A myopic person has been using spectacles of power -1.0 dioptre for distant vision. During old age he also needs to use separate reading glasses of power +2.0 dioptres. Explain what may have happened.
Answer:
Given P = - 1.0 dioptre
∴ f = \(\frac{100}{1}\) = - 100 cm
Another lens had power P₁ = +2.0 dioptre
∴ f₁ = \(\frac{100}{2}\) = 50 cm
Thus the far point of the person is 100 cm, while his near point may have normal (about 25 cm). Object at infinity produces virtual image at 100 cm (using spectacles). To view closer objects i.e., those which are (or whose images using the spectacles are) between 100 cm and 25, the person uses the ability of accommodation of his eye lens. This ability usually gets partially lost in old age (presbyopia). The near point of the person recedes to 50 cm To view objects at 25 cm clearly, the person needs converging lens of power +2 dioptre.

Question 9.27.
A person looking at a person wearing a shirt with a pattern comprising vertical and horizontal lines is able to see the vertical lines more distinctly than the horizontal lines. What is the defect due to? How is such a defect of vision corrected?
Answer:
The defect (called astigmatism) arises because the curvature of the cornea plus eye lens refracting system is not the same in different planes. [The eye lens is usually spherical i.e., has the same curvature on different planes but the cornea is not spherical in case of an astigmatic eye]. In the present case, the curvature in the vertical plane is enough, so sharp images of vertical lines can be formed on the retina. But the curvature is insufficient in the horizontal plane, so horizontal lines appear blurred. The defect can be corrected by using a cylindrical lens with its axis along the vertical. Clearly parallel rays in the vertical plane will suffer no extra refraction, but those in the horizontal can get the required extra convergence due to refraction by the curved surface of the cylindrical lens if the curvature of the cylindrical surface is chosen appropriately.

Question 9.28.
A man with near normal point (25 cm) reads a book with small print using a magnifying glass: a thin convex lens of focal length 5 cm
(а) What is the closest and farthest distance at which he should keep the lens from the page so that he can read the book when viewing through the magnifying glass?
(b) What is the maximum and the minimum angular magnification (magnifying power) possible using the above simple microscope?
Answer:
Given v = -25 cm, f = 5 cm
(a) Closest distance, u =?
Since \(-\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)
∴ u = \(\frac{v f}{f-u}=\frac{(-25) \times 5}{5+25}=\frac{-125}{30}=\frac{-25}{6}\) = 4.2 cm
Farther distance u₁ =?
Here v₁ = ∞
So \(-\frac{1}{u_1}+\frac{1}{v_1}=\frac{1}{f}\)
or f = u₁ = -5 cm

(b) Maximum angular magnification = \(\frac{f}{u_1}=\frac{25}{25 / 6}\) = 6
Minimum angular magnification = \(\frac{f}{u_1}=\frac{25}{5}\) = 5

Question 9.29.
A card sheet divided into squares each of size 1 mm² is being viewed at a distance of 9 cm through a magnifying glass (a converging lens of focal length 9 cm) held close to the eye.
(a) What is the magnification produced by the lens? How much is the area of each square in the virtual image?
(b) What is the angular magnification (magnifying power) of the lens?
(c) Is the magnification in (a) equal to the magnifying power in (b)? Explain.
Answer:
(a) Given u = - 9 cm, v = ?, f = 10 cm

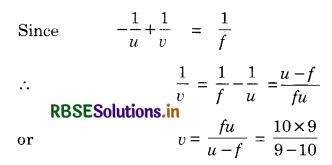
= -90 cm
∴ Magnitude of magnification
\(\frac{90}{9}\) = 10 cm
Each square in the virtual image has an area
= (10 x 10) mm²
= 100 mm² = 1 cm²
(b) Magnifying power = 25/9 = 2.8.

(c) No, magnification of image by a lens and angular magnification (or magnifying power) of an optical instrument are two separate things. The latter is the ratio of the angular size of the object (which is equal to the angular size of the image even if the image is magnified) to the angular size of the object if placed at the near point (25 cm). Thus, magnification magnitude is | (v/u) | and magnifying power is (25/|u |). Only when the image is located at the near point | v | = 25 cm are the two quantities equal.

Question 9.30.
(i) At what distance should the lens be held from the card sheet in Q. 9.29 in order to view the square distinctly with the maximum possible magnifying power?
(ii) What is the magnification in this case?
(iii) Is the magnification equal to magnifying power in this case? Explain.
Answer:
(i) Maximum magnifying power is obtained when the image is the near point (25 cm).
∴ v    = -25 cm
f = 10cm

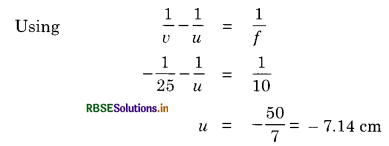
(ii) Magnitude of magnification
m = \(\frac{25}{u}=\frac{25}{7.14}\) = 35

(iii) Magnifying power = \(\left(1+\frac{D}{f}\right)=\left(1+\frac{25}{10}\right)\) = 3.5
Yes, the magnifying power (when the image is produced at 25 cm) is equal to the magnitude of magnification.
 
Question 9.31.
What should be the distance between the object in Q. 9.30 and the magnifying glass if the virtual image of each square is to have an area of 6.25 mm²? Would you be able to see the squares distinctly with your eyes close to the magnifier.
Note. Exercises 9.29 to 9.31 will help you clearly understand the difference between magnification in absolute size and the angular magnification (or magnifying power) of an instrument.
Answer:
Linear magnification,
m = \(\frac{\sqrt{6.25}}{1}\) = 2.5
∴ \(\frac{v}{u}\) = 2.5
v = +2.5 u
Using the relation,
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
\(+\frac{1}{2.5 u}-\frac{1}{u}=\frac{1}{10}\)
u = -6 cm
|v| = 2.5 x 6 = 15 cm
The virtual image is closer than the normal near point (25 cm) and cannot be seen by the eye distinctly.

Question 9.32.
Answer the following questions:
(a) The angle subtended at the eye by an object is equal to the angle subtended at the eye by the virtual image produced by a magnifying glass, In what sense then does a magnifying glass provide angular magnification?
(b) In viewing through a magnifying glass, one usually positions one’s eyes very close to the lens. Does angular magnification change if the eye is moved back?
(c) Magnifying power of a simple microscope is inversely proportional to the focal length of the lens. What then stops us from using a convex lens of smaller and smaller focal lengths and achieving greater and greater magnifying power?
(d) Why must both the objective and the eyepiece of a compound microscope have short focal lengths?
(e) When viewing through a compound microscope, our eyes should be positioned not on the eyepiece but a short distance away from it for best viewing. Why? How much should be that short distance between the eye and eyepiece?
Answer:
(a) Even though the absolute image size is bigger than object size, the angular size of the image is equal to the angular size of the object. The magnifier helps in the following way: Without it the object would be placed not closer than 25 cm; with it the object can be placed much closer. The closer object can be placed much closer. The closer object has large angular size than the same object at 25 cm. It is in this sense that angular magnification is achieved.

(b) Yes, it decreases a little because the angle subtended at the eye is then slightly less than the angle subtended at the lens. The effect is negligible if the image is at very large distance away.

(c) First, grinding lenses of very small focal lengths is not easy. More important, if you decrease focal length, aberrations (both spherical and chromatic) become more pronounced.

(d) Angular magnification of eyepiece is \(\frac{25}{f_e}\) +1 (f_e in cm) which increase if f_e is smaller. Further, magnification of the objective is given by \(\frac{v_0}{u}=\frac{1}{\frac{u}{f}-1}\) which is large when u₀ is slightly small than f₀. Now the microscope is used for viewing very close objects. So u is small, and so is f₀.

(e) If we place our eyes too close to the eyepiece, we shall not collect much of the light and also reduce our field of view. If we position our eyes on the eye ring and the area of the pupil of our eye is greater or equal to the area of the eye ring, our eyes will collect the light refracted by the objective.

Question 9.33.
An angular magnification (magnifying power) of 30 X is desired using an objective of focal length 1.25 cm and an eyepiece of focal length 5 cm. How will you set up the compound microscope?
Answer:
Assume microscope in normal use i.e. image at 25 cm
Angular magnification of the eyepiece
= \(\left(1+\frac{\mathrm{D}}{f}\right)\)
= 1 + \(\frac{25}{5}\) = 6
Magnification of the objective = \(\frac{30}{6}\) = 5
m = \(\frac{v}{u}\) = 5 (∵ v = 5u)
-\(\frac{1}{5 u}-\frac{1}{u}=\frac{1}{1.25}\)
u = -1.5 m
|v | = 5 x 1.5 = 7.5 cm
|u| = \(\frac{25}{6}\) = 4.17 cm
The separation between the objective and eyepiece should be 
|v| + |u| = 7.5 + 4.17 = 11.67 cm
Further, the object should be placed 1.5 cm from the objective to obtain the desired magnification.

Question 9.34.
A small telescope has an objective lens of focal length 140 cm and eyepiece of focal length 5.0 cm. What is the magnifying power of the telescope for viewing distant objects when:
(a) the telescope is in normal adjustment (i.e. when the final image is at infinity)?
(b) the final image is formed at the least distance of the distinct vision (25 cm)?
Answer:
(a) For normal adjustment
M.P. of telescope = \(\frac{f_0}{f_e}=\frac{140}{5}\) = 28

(b) When image is at the least distance of distinct vision
M.P. = \(\frac{f_0}{f_e}\left(1+\frac{f_e}{25}\right)\)
= 28\(\left(1+\frac{5}{25}\right)\)
= 28 x 1.2 = 33.6.

Question 9.35.
(a) For the telescope described in Q. 9.34 (a), what is the separation between the objective lens and eyepiece?
b) If this telescope is used to view a 100 m tall tower 3 km away, what is the height of the image of the tower formed by the objective lens?
(c) What is the height of the final image on the tower if it is formed at 25 cm?
Answer:
(a) f₀ + f_e = 140 + 5 = 145 cm

(b) Angle subtended by the tower
= \(\frac{100}{3000}=\frac{1}{30}\) rad ..................(i)
Angle subtended by the image produced by the objective
= \(\frac{h}{f_0}=\frac{h}{140}\) ....................(ii)
Equating (i) and (ii), we get
\(\frac{h}{140}=\frac{1}{30}\)
h = \(\frac{14}{3}\) cm = 4.7 cm

(c) Magnification (magnitude) of the eyepiece
= 1 + \(\frac{\mathrm{D}}{f}\) = 1 + \(\frac{\mathrm{25}}{5}\) = 6
Height of the final image (magnitude)
= \(\frac{14}{3}\) x 6 = 28 cm

Question 9.36.
A Cassegrain telescope uses two mirrors as shown in figure TBQ 9.36. Such a telescope is built with mirrors, 20 mm apart. If the radius of curvature of the large mirror is 220 mm and the small mirror is 140 mm, where will the final image of an object at infinity be?

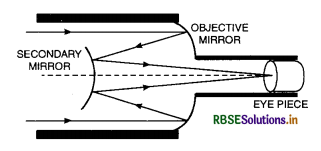
Answer:
The image formed by the large (concave) mirror acts as virtual object for the smaller (convex) mirror. Parallel rays coming from the object at infinity will focus at a distance of 110 mm from the large mirror.
The distance of virtual object for the smaller mirror.
= 110 - 20 = 90 mm
The focal length of smaller mirror = 70 mm

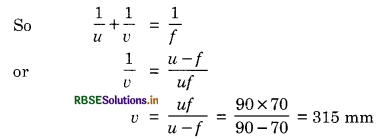
from the smaller mirror.

Question 9.37.
Light incident normally on a plane attached to a galvanometer coil retraces backward as shown in Fig. TBQ 9.37. A current in the coil produces a deflection of 3.5° of the mirror. What is the displacement of the reflected spot of light on a screen placed 1.5 m away?

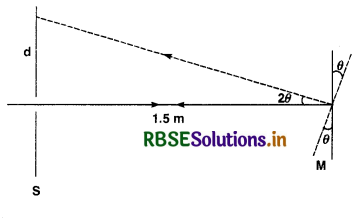
Answer:
In Fig. 9.12 the ray gets reflected by twice the angle of rotation of the mirror.
\(\frac{d}{15}\) = tan 2θ
\(\frac{d}{1.5}\) = tan 7° = 0.1228
d = 1.5 x 0.1228
= 0.1842 m.
= 18.42

Question 9.38.
Figure TBQ 9.38 shows an equiconvex lens (of refractive index 1.50) in contact with a liquid layer on top of a plane mirror. A small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be 45.0 cm. The liquid is removed and the experiment is repeated. The new distance is measured to be 30.0 cm. What is the refractive index of the liquid?

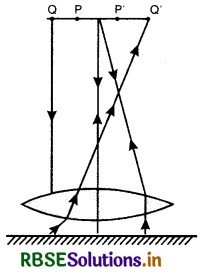
Answer:
Here µ = 1.5 and 45 cm in focal length f of the combination of convex lens and piano concave liquid lens.
When liquid is removed, then f₁ = 30 cm is focal length of convex lens only. If f₂ is focal length of piano concave liquid lens, then from

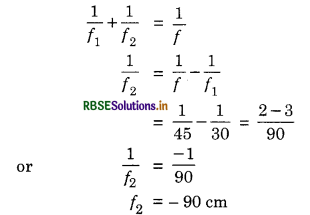
Using lens maker’s formula for equiconvex lens where in
R₁ = R₂ = R

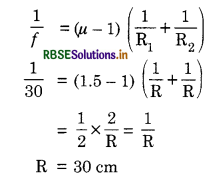
For plano-concave lens of liquid.
f₂ = -90 cm, µ = ?
R₁ = ∞ (for plane surface)
R₂ = R = -30 cm
As \(\frac{1}{f_2}=(\mu-1)\left(\frac{1}{R_1}+\frac{1}{R_2}\right)\)

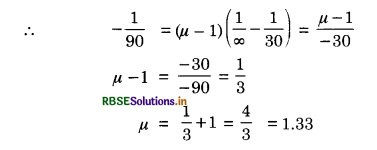
SELECTED EXEMPLAR PROBLEMS

MCQ I [with one correct option]

Question 9.1.
A ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5° and the prism is made of a material of refractive index 1.5, the angle of incidence is:
(a) 7.5°
(b) 5°
(c) 15°
(d) 2.5°.
Answer:
(a) Given i₂ = 0° so r₂ = 0°
Also r₁ + r₂ = A
So r₁ = A - r₂ = 5 - 0 = 5°
As µ = \(\frac{\sin i_1}{\sin r_1}\)
⇒ sini = µ sin r₁
= 1.5 x sin 5° = 1.5 x 0.087
or i₁ = sin^-1 (0.1305) = 7.5°

Question 9.2.
A short pulse of white light is incident from air to a glass slab at normal incidence. After traveling through the slab, the first color to emerge is:
(a) blue
(b) green
(c) violet
(d) red.
Answer:
(d) As velocity v ∝ λ. Red color has the highest wavelength, so its speed will also be highest.

Question 9.3.
An object approaches a convergent lens from the left of the lens with a uniform speed 5m/s and stops at the focus. The image
(а) moves away from the lens with a uniform speed 5m/s
(b) moves away from the lens with a uniform acceleration.
(c) moves away from the lens with a non-uniform acceleration.
(d) moves towards the lens with a non-uniform acceleration.
Answer:
(c) The image moves away from the lens with non-uniform acceleration.

Question 9.4.
A passenger in an airplane shall 
(a) never see a rainbow.
(b) may see a primary and a secondary rainbow as concentric circles
(c) may see a primary and a secondary rainbow as concentric arcs. 
(d) shall never see a secondary rainbow.
Answer:
(b) In an airplane a passenger sees a primary and secondary rainbow as concentric circles as he can also see the lower arc of rainbow which a person the surface of earth cannot see.

Question 9.5.
The phenomena involved in the reflection of radiowaves by ionosphere is similar to
(а) reflection of light by a plane mirror.
(b) total internal reflection of light in air during a mirage.
(c) dispersion of light by water molecules during the formation of a rainbow
(d) scattering of light by the particles of air.
Answer:
(b) Total Internal reflection of light

Question 9.6.
The direction of ray of light incident on a concave mirror is shown by PQ while directions in which the ray would travel after reflection is shown by four rays marked 1, 2, 3 and 4 (Fig. EP 9.8). Which of the four rays correctly shows the direction of reflected ray?
(a) 1    
(b) 2
(c) 3
(d) 4.

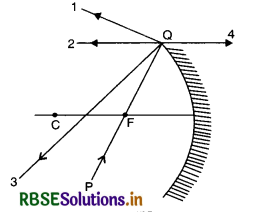
Answer:
(b) A ray of light incident on a concave mirror through F must go parallel to the principal axis.

Question 9.7.
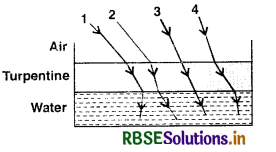
The optical density of turpentine is higher than that of water while its mass density is lower. Fig. EP 9.9 shows a layer of turpentine floating over water in a container. For which one of the four rays incident on turpentine in Fig. 9.15 the path shown is correct?
(a) 1
(b) 2
(c) 3
(d) 4.

Answer:
(b) When a ray goes from air to turpentine it bends towards the normal (rarer to denser) and from turpentine to water it bends away from the normal [denser to rarer].

Question 9.8.
A car is moving at a constant speed of 60 km h-1 on a straight road. Looking at the rear view mirror, the driver finds that the car following him is at a distance of 100 m and is approaching with a speed of 5 km h-1. In order to keep track of the car in the rear, the driver begins to glance’ alternatively at the rear and side mirror of his car after every 2 s till the other car overtakes. If the two cars were maintaining their speeds, which of the following statement(s) is/are correct?
(a) The speed of the car in the rear is 65 km h-1
(b) In the side mirror the car in the rear would appear to approach with a speed of 5 km h-1 to the driver of the leading car
(c) In the rearview mirror the speed of the approaching car would appear to decrease as the distance between the cars decreases.
(d) In the side mirror, the speed of the approaching car would appear to increase as the distance between the cars decreases.
Answer:
(d) In the side mirror, the speed of the approaching car would appear to increase as the distance between the cars decreases.

Question 9.9. 
A rectangular block of glass ABCD has a refractive index 1.6. A pin is placed midway on the face AB (Fig. EP 9.12). When observed from the face AD, the pin shall
(а) appear to be near A.
(b) appear to be near D.
(c) appear to be at the center of AD.
(d) not be seen at all.

Answer:
(d) Critical angle is given as
µ = \(\frac{1}{\sin C}\)
So sin C = \(\frac{1}{\mu}=\frac{1}{1.6}\) = 0.625
So C = 38.7°
When observed from face AD, if angle of incidence on AD will be more than critical angle there will be total internal reflection and the pin will not be seen at all.

MCQ II. (with more than one correct option)

Question 9.10.
Consider an extended object immersed in water contained in a plane trough. When seen from close to the edge of the trough the object looks distorted because
(а) the apparent depth of the points close to the edge are nearer the surface of the water compared to the points away from the edge.
(b) the angle subtended by the image of the object at the eye is smaller than the actual angle subtended by the object in air.
(c) some of the points of the object far away from the edge may not be visible because of total internal reflection
(d) water in a trough acts as a lens and magnifies the object.
Answer:
(a), (b) and (c).
Here option (d) is incorrect.

Question 9.11.
Between the primary and secondary rainbows, there is a dark band known as Alexandar’s dark band. This is because
(а) light scattered into this region interferes destructively.
(b) there is no light scattered into this region.
(c) light is absorbed in this region.
(d) angle made at the eye by the scattered rays with respect to the incident light of the sun lies between approximately 42° and 50°.
Answer:
(a), (d), options. (b) and (c) are incorrect.

Question 9.12.
A magnifying glass is used, as the object to be viewed can be brought closer to the eye than the normal near point. This results in
(а) a larger angle to be subtended by the object at the eye and hence viewed in greater detail.
(b) the formation of a virtual erect image
(c) increase in the field of view
(d) infinite magnification at the near point.
Answer:
(a), (b) options, (c) and (d) are incorrect. 

Question 9.13.
An astronomical refractive telescope has an objective of focal length 20 m and an eyepiece of focal length 2 cm.
(a) The length of the telescope tube is 20.02 m.
(b) The magnification is 1000.
(c) The image formed is inverted.
(d) An objective of a larger aperture will increase the brightness and reduce chromatic aberration of the image.
Answer:
(a), (b), (c)
Length of the telescope f₀ + f_e = 20 + 0.02 = 20.02 m
Magnification m = \(\frac{20}{0.02}\) = 1000
Also image is inverted.

Very Short Answer Type Questions

Question 9.14.
Will the focal length of a lens for red light be more, same or less than that for blue light?
Answer:
Since \(\frac{1}{f}=(\mu-1)\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right)\)
As µ_r < µ_b
f_r > f_b

Question 9.15.
The near vision of an average person is 25 cm. To view an object with an angular magnification of 10, what should be the power of the microscope?
Answer:
Angular magnification

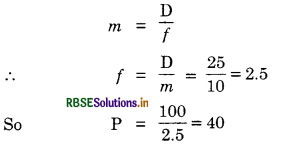
Question 9.16.
An unsymmetrical double convex thin lens forms the image of a point object on its axis. Will the position of the image change if the lens is reversed?
Answer:
No, because
\(\frac{1}{f} = (µ - 1) \left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)
= (µ - 1) \(\left(\frac{1}{R_2}-\frac{1}{R_1}\right)\)
So when the lens is reversed, R₁ and R₂ reversed and so their signs.

Question 9.17.
For a glass prism (µ = \(\sqrt{3}\)) the angle of minimum deviation is equal to the angle of the prism. Find the angle of the prism.
Answer:
We know that

Short Answer Type Questions

Question 9.18.
A thin convex lens of focal length 25 cm is cut into two pieces 0.5 cm above the principal axis. The top part is placed at (0, 0) and an object placed at (- 50 cm, 0). Find the coordinates of the image.
Answer:
OO' is principal axis when there was no cut

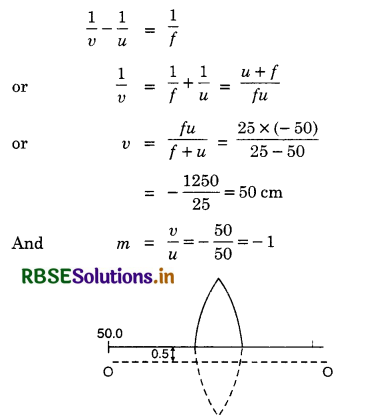
Thus the image would have been formed at 50 cm from the pole and 0.5 cm below the principal axis. Hence with respect to the x-axis passing through the edge of the cut lens, the coordinates of the image are (50 cm, -1 cm).

Question 9.19.
A jar of height h is filled with a transparent liquid of refractive index µ (Fig. EP 9.26). At the center of the jar on the bottom surface is a dot. Find the minimum diameter of a disc, such that when placed on the top surface symmetrically about the centre, the dot is invisible.

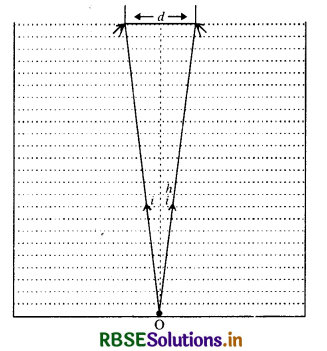
Answer:
Let d be diameter of the disc. The spot shall be invisible if the incident rays from the dot at O to the surface at \(\frac{d}{2}\) are at the critical angle.
Let angle of incidence be i.
Since sin i = \(\frac{1}{\mu}\)
From the figure

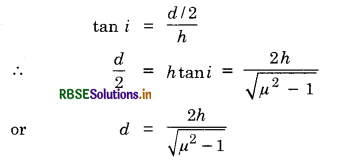
Question 9.20.
A myopic adult has a far point at 0.1 m. His power of accommodation is 4 dioptres, (i) What power lenses are required to see distant objects? (ii) What is his near point without glasses? (iii) What is his near point with glasses? (Take the image distance from the lens of the eye to the retina to be 2 cm.)
Answer:
(i) Let the power at the far point be P_f for normal relaxed eye of an average person. 
The required power. P_f = \(\frac{1}{v}-\frac{1}{u}=\frac{1}{0.02}+\frac{1}{0.1}\)
= 50 + 10 = 60 D
With the corrective lens, the object distance at the far point is ∞:
Required power, P'_f = \(\frac{1}{1.02}-\frac{1}{\infty}\) = 50D
Required power of glasses, P_g = P'_f - P_f = 50 - 60 = - 10D

(ii) Power of accommodation is 4D for the normal eye.
If Pn is the power of normal eye for near vision, then
u = P_n - P_f = P_n - 60
or P_n = 4 + 60 = 64D
Let the near point without glasses be X_n, then
\(\frac{1}{\mathrm{X}_n}+\frac{1}{0.02}\) = 64
or X_n = 0.07 m

(iii) With glasses, P_n = P'_f + 4 = 50 + 4 = 54 
54 = \(\frac{1}{\mathrm{X}_n^{\prime}}+\frac{1}{0.02}=\frac{1}{\mathrm{X}_n^{\prime}}\) + 50
or \(\frac{1}{\mathrm{X}_n^{\prime}}\) = 4 ⇒ X_n' = \(\frac{1}{4}\) = 0.25 m

Long Answer Type Questions

Question 9.21.
Show that for a material with refractive index µ ≥ \(\sqrt{2}\), light incident at any angle shall be guided along a length perpendicular to the incident face.
Ans. Any incident ray falling on AB face shall fall on AC if the angle made on face AC (i.e. Φ) is more than the critical angle as shown in the figure. EP 9.28.

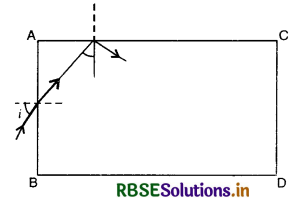
Then sin Φ ≥ \(\frac{1}{\mu}\)
or sin (90° - r) ≥ \(\frac{1}{\mu}\)

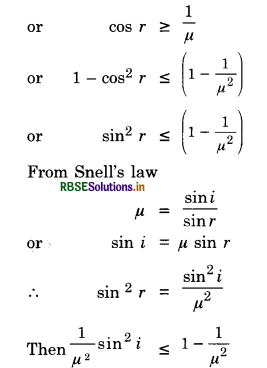
i.e. sin² i ≤ µ² - 1
Φ will be the smallest when i = 90°. If that is greater than the critical angle then all other angles then all other angles of incidence shall be more than critical angle.
Thus 1 ≤ µ² - 1
or µ² ≥ 2
or µ ≥ \(\sqrt{2}\)

Question 9.22.
The mixture a pure liquid and a solution in a long vertical column (i.e., horizontal dimensions << vertical dimensions) produces diffusion of solute particles and hence a refractive index gradient along the vertical dimension. A ray of light entering the column at right angles to the vertical is deviated from its original path. Find the deviation in traveling a horizontal distance d << h, the height of the column.
Answer:
Here ray of light at (x, y) enters at 90°. Consider a portion of the ray between x and x + dx inside the liquid. The ray deviates at angle dθ between x and x + dx, emerging at (x + dx, y + dy) at angle θ + dθ while entering at θ, at height ay and y + dy.
From Snell’s law
µ (y) sin θ ≃ µ (y + dy) sin (θ + dθ)
or µ (y) sin θ ≃ \(\left(\mu(y)+\frac{d \mu}{d y} d y\right)\) (sin θ cos dθ + cos θ sin dθ)
As dθ is small, cos dθ - 1 and sin dθ = dθ
∴ µ (y) sin θ = µ (y) sin θ + µ (y) cos θ dθ + \(\frac{d \mu}{d y}\) sin θ
(fourth term is negligibly small and hence neglected)

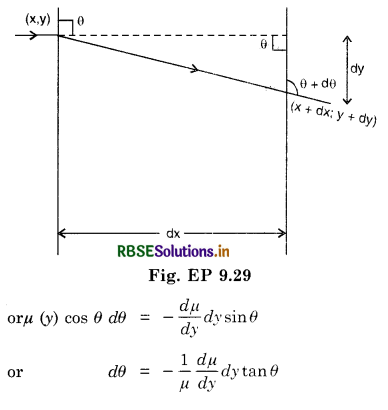
But from the figure, we find tan θ = \(\frac{d x}{d y}\)
⇒ dy tan θ = dx
So dθ = \(-\frac{1}{\mu} \frac{d \mu}{d y}\) d x
or θ = \(-\frac{1}{\mu} \frac{d \mu}{d y} \int_0^d d x=-\frac{1}{\mu} \frac{d \mu}{d y}(d)\)
This is the deviation in traveling a horizontal distance d.

Question 9.23.
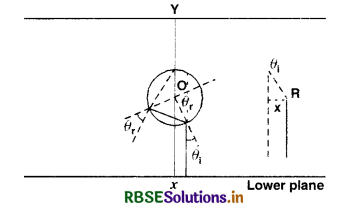
An infinitely long cylinder of radius R is made of an unusual exotic material with refractive index - 1 (Fig. EP 9.31). The cylinder is placed between two planes whose normals are along the y direction. The center of cylinder O lies along the y-axis. A narrow laser beam is directed along the y direction from the lower plate. The laser source is at a horizontal distance x from the diameter in the y direction. Find the range of x such that light emitted from the lower plane does not reach the upper plane.

Answer:
As the material is of refractive index -1,θ_r is negative and θ'_r positive.
|θ_i| = |θ_r| = |θ_r'|
The total deviation of the outcoming ray from the incoming ray is 4θi.
Rays shall not reach the receiving plate if
\(\frac{\pi}{2} \leq 4 \theta_i \leq \frac{3 \pi}{2}\)
(Angles measured clockwise from the y-axis) 
or \(\frac{\pi}{8} \leq 4 \theta_i \leq \frac{3 \pi}{8}\)
From the figure

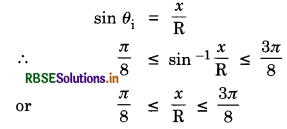
Thus for \(\frac{\mathrm{R} \pi}{8} \leq x \leq \frac{\mathrm{R} 3 \pi}{8}\) light emitted from the source shall not reach the receiving plate.