RBSE Solutions for Class 12 Physics Chapter 8 Electromagnetic Waves

Rajasthan Board RBSE Solutions for Class 12 Physics Chapter 8 Electromagnetic Waves Textbook Exercise Questions and Answers.

RBSE Class 12 Physics Solutions Chapter 8 Electromagnetic Waves

RBSE Class 12 Physics Electromagnetic Waves Textbook Questions and Answers

Question 8.1.
Fig. TBQ 8.1 shows a capacitor made of two circular plates each of radius 12 cm and separated by 5.0 cm. The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to 0.15 A.

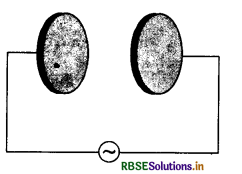
(a) Calculate the capacitance and rate of change of the potential difference between the plates.
(b) Obtain the displacement current across the plates.
(c) Is Kirchhoff's first rule (junction rule) valid at each plate of the capacitor? Explain.
Answer:
r = 0.12 m,
d = 5.0 cm = 5 x 10^-2 m,
I = 0.15 A

(a) Capacitance of the capacitor,

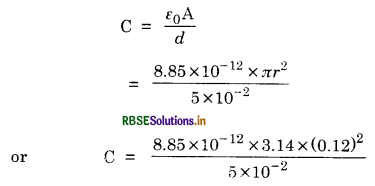
= 8 x 10^-12 F = 8 µF
Since I = \(\frac{d q}{d t}=\frac{d}{d t}\)(CV)
or I = C\(\frac{d \mathrm{~V}}{d t}\)
∴ \(\frac{d \mathrm{~V}}{d t} = \frac{\mathrm{I}}{\mathrm{C}}=\frac{0.15}{8 \times 10^{-12}}\)
= 1.87 x 10¹⁰ Vs^-1

(b) Displacement current (I_d) = conduction current (I) = 0.15 A.

(c) Yes, Kirchhoff's first law holds good at each plate if we take both conduction and displacement current. The conduction current arriving at a plate is equal to the displacement current leaving that plate.

Question 8.2.
A parallel plate capacitor (Fig. TBQ 8.2) made of circular plates each of radius R = 6.0 cm has a capacitance C = 100 pF. The capacitor is connected to a 230 V a.c. supply with an (angular) frequency of 300 rad^-1 s.
(a) What is r.m.s. value of conduction current?
(b) Is the conduction current equal to the displacement current?
(c) Determine the amplitude of B at a point 3.0 cm from the axis between the plates.

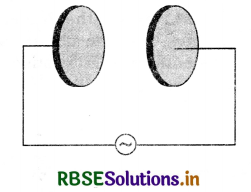
Answer:
R = 6.0 cm = 6 x 10^-2 m,
C = 100 pF = 10^-10 F,
Ev = 230 V.
ω = 300 rad s^-1, Area of the plate A = πR²

(a) I_v = \(\frac{\mathrm{E}_v}{\mathrm{X}_{\mathrm{C}}}\) = E_vωC
= 230 x 300 x 10^-10
= 6.9 x 10^-6  = 6.9 µF

(b) Displacement current is always equal to conduction current as shown below:
I_d = ε₀ \(\frac{d \phi}{d t} = \frac{\varepsilon d}{d t}\)(EA)
= ε₀ \(\frac{d}{d t}\left(\frac{q}{\varepsilon_0 \mathrm{~A}} \mathrm{~A}\right)\)
or I_d = ε₀ \(\frac{1}{\varepsilon_0} \frac{d q}{d t}=\frac{d q}{d t}\)
= I (conduction current)

(c) Consider a loop of radius r between the two circular plates.
The area of the loop A' = πr²
By symmetry, magnetic field induction  \(\vec{B}\)  is equal in magnitude and is tangential to the circle at every point. Here only displacement current will cross the loop.
For r < R, using Maxwell-Ampere’s law, we get
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{dl}}\) = µ₀I
or B x 2πr = µ₀I_d (through area A')
= µ₀I_d\(\frac{\pi r^2}{\pi R^2}\)
or B = \(\frac{\mu_0 I_d r}{2 \pi R^2}=\frac{\mu_0 \mathrm{Ir}}{2 \pi \mathrm{R}^2}\) [∴ I_d = I]
Since the capacitor is connected to the alternating voltage, so the magnetic field within the capacitor plates is alternating.
Let B = B₀ cos ωt
∴ Amplitude of B = B₀ = maximum value of B

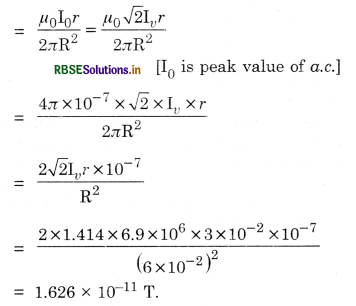
Question 8.3.
What physical quantity is the same for X-rays of wavelength 10^-10 m, red light of wavelength 6800 A and radio waves of wavelength 500 m?
Answer:
The speed in vacuum is the same for all.
c = 3 x 10⁸ ms^-1.

Question 8.4.
A plane electromagnetic wave travels in vacuum along z-direction. What can you say about the direction of its electric and magnetic field vectors? If the frequency of the wave is 30 MHz, what is its wavelength?
Answer:
\(\overrightarrow{\mathrm{E}}\) and \(\overrightarrow{\mathrm{B}}\) are in x-y plane and are mutually perpendicular.
Given v = 30 MHz = 30 x 10⁶ Hz
c = 3 x 10⁸ ms^-1
∴ λ = \(\frac{c}{v}=\frac{3 \times 10^8}{30 \times 10^6}\) = 10 m.

Question 8.5.
A radio can tune in to any station in the 7.5 MHz to 12 MHz bands. What is the corresponding wavelength band?
Answer:
For v₁ = 7.5 MHz = 7.5 x 10⁶ Hz
λ₁ = \(\frac{c}{v_1}=\frac{3 \times 10^8}{7.5 \times 10^6}\) = 40 m
For v₂ = 12 MHz = 12 x 10⁶ Hz
λ₂ = \(\frac{c}{v_2}=\frac{3 \times 10^8}{12 \times 10^6}\) = 25 m
So the wavelength band: 40 m to 25 m.

Question 8.6.
A charged particle oscillates about its mean equilibrium position with a frequency of 10⁹ Hz. What is the frequency of the electromagnetic waves produced by the oscillator?
Answer:
The frequency of e.m. waves produced by the oscillator is equal to the frequency of oscillation of the charged particle about its mean position i.e. 10⁹ Hz.

Question 8.7.
The amplitude of the magnetic field part of a harmonic electromagnetic wave in vacuum is B₀ = 510 nT. What is the amplitude of the electric field part of the wave?
Answer:
Given B₀ = 510 nT = 510 x 10^-9 T
∴ E₀ = B₀c = 510 x 10^-9 x 3 x 10⁸
= 153 NC^-1.

Question 8.8.
Suppose that the electric field amplitude of an electromagnetic wave is E₀ = 120 NC^-1 and that its frequency is n = 50.0 MHz. (a) Determine, \(\vec{B}_0\),ω, k and λ.
(b) Find expressions for E and B.
Answer:
Given E₀ = 120 NC^-1
v = 50.0 MHz = 50 x 10⁶ Hz

(a) B₀ = \(\frac{E_0}{c}=\frac{120}{3 \times 10^8}\)
= 40 x 10^-8 T
or B₀ = 400 nT
ω = 2πv = 2 x 3.14 x 50 x 10⁶
= 3.14 x 10⁸ rad s^-1
λ = \(\frac{c}{v}=\frac{3 \times 10^8}{50 \times 10^6}\)
or λ = 6.00 m
And k = \(\frac{2 \pi}{\lambda}=\frac{2 \times 3.142}{6}\)
= 0.05 rad m^-1

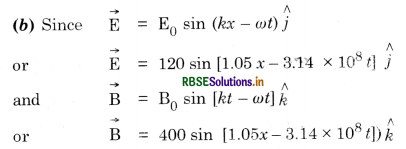
Question 8.9.
The terminology for different parts of the electromagnetic spectrum is given in the text, use the formula E = hv (for energy of a quantum of radiation: photon) and obtain the photon energy in units of eV for different parts of the e.m. spectrum. In what way are the different scales of photon energies that you obtain related to the sources of electromagnetic radiation?
Answer:
Photon energy for λ = 1m is,
E = \(\frac{h c}{\lambda} \)
E = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{1.6 \times 10^{19}}\) eV
= 1.24 x 10^-6 eV
Photon energy for other wavelengths in the figure for e.m. spectrum can be obtained by multiplying appropriate powers of ten. Energy of a photon that a source produces indicates the spacing of the relevant energy levels of the sources. For example λ = 1.0-12 m corresponds to photon energy = 1.24 x 10⁶ eV = 1.24 MeV. This indicates that nuclear energy levels (transition between which cause γ-ray emission) are typically spaced by 1 MeV or so. Similarly, a visible wavelength λ = 2 x 10^-7 m corresponds to photon energy = 2.5 eV. This implies that energy levels (transitions between which give visible radiation) are typically spaced by a few eV.

Question 8.10.
In a plane e.m. wave, the electric field oscillates sinusoidally at a frequency of 2.0 x 10¹⁰ Hz and amplitude 48 Vm^-1.
(a) What is the wavelength of the wave?
(b) What is the amplitude of the oscillating magnetic field?
(c) Show that the average energy density of the E field equals to the average energy density of the B field, [c = 3.0 x 10⁸ ms^-1]
Answer:
(a) λ = \(\frac{c}{v}=\frac{3 \times 10^8}{2.0 \times 10^{10}}\)
= 1.5 x 10^-2 m
E = 48 Vm^-1

(b) B₀ = \(\frac{\mathrm{E}_0}{c}=\frac{48}{3 \times 10^8}\)
or B₀ = 1.6 x 10^-7 T

(c) Energy density in \(\vec{E}\) field,
U_E = \(\frac{1}{2}\)ε₀E²
Energy density in B field, U_B = \(\frac{1}{2 \mu_0}\)B²
Using E = cB and c = \(\frac{1}{\sqrt{\mu_0 \varepsilon_0}}\),
We find that U_E = U_B.

ADDITIONAL EXERCISES

Question 8.11.
Suppose that the electric field part of an electromagnetic wave in vacuum is
\(\overrightarrow{\mathbf{E}}\) = {(3.1 N/C) cos [(1.8 rad/m) y + (5.4 x 106 rad-s^-1t)]}\( \hat{i}\).
(а) What is the direction of propagation?
(b) What is the wavelength λ?
(c) What is the frequency v?
(d) What is the amplitude of the magnetic field part of the wave?
(e) Write an expression for the magnetic field part of the wave.
Answer:
(a) - \(\hat{j}\)

(b) λ = \(\frac{2 \pi}{k}=\frac{2 \times 3.14}{1.8}\) = 3.48
= 3.5 m

(c) v = c/λ = \(\frac{3 \times 10^8}{3.5}\)
= 85.7 x 10⁶ = 86 MHz

(d) B₀ = \(\frac{\mathrm{E}_0}{c}=\frac{31}{3 \times 10^8}\)
= 10.3 x 10^-8 T = 100.3 nT

(e) (100 nT) cos [(1.8 rad/m) y + (5.4 x 10⁶ rad/s)t] \(\hat{k}\).

Question 8.12.
About 5% of the power of a 100 W light bulb is converted to visible radiation. What is the average intensity of visible radiation?
(а) At a distance of 1 m from the bulb?
(b) At a distance of 10 m?
Assume that the radiation is emitted isotropically and neglects reflection.
Answer:
(a) At a distance of 1m, the surface area of the surrounding sphere 
A = 4πr² = 4 x 3.14 x 12
= 12.56 m²
∴ Intensity at this distance
I = \(\frac{\text { Power }}{\text { Area }}=\frac{100 \mathrm{~W} \times 5 \%}{12.56}\)
= 0.39
or I = 0.4 Wm^-2

(b) At a distance 10 m A₁ = 4πr₁² = 4 x 3.14 x 100
= 1256 m²
∴ I₁ = \(\frac{\text { Power }}{\text { Area }}=\frac{100 \mathrm{~W} \times 5 \%}{1256}\)
= 0.004 Wm^-2

Question 8.13.
Use the formula λ_m T = 0.29 cm K to obtain the characteristic temperature range for different parts of the e.m. spectrum. What do the numbers that you obtain tell you?
Answer:
Here λ_mT = 0.29 cm K
∴ T = \(\frac{0.29}{\lambda_m}\)
If λ_m = 10^-6 m = 10^-4 cm, then
T = \(\frac{0.29}{10^{-4}}\) = 2900 K
Similarly, temperature for other wavelengths can be found. These numbers provide the temperature ranges required for obtaining radiations in the various parts of e.m. spectrum. If we consider visible radiation of wavelength λ = 5 x 10^-5 m.
Then T = \(\frac{0.29}{5 \times 10^{-5}}\) ≅ 5800 K.

Question 8.14.
Magnetic field lines can neither emanate from a point nor end on a point. Yet the field lines outside a bar magnet do seem to start from the North pole and end on the South pole. Does the second fact contradict the first? Explain.
Answer:
There is no contradiction. Field lines inside the bar go away from S towards N. The next flux of B over any surface fully enclosing N or S must be identically zero.

Question 8.15.
Given below are some famous numbers associated with electromagnetic radiations in different contexts in physics. State the part of the e.m. spectrum to which each belongs.
(a) 21 cm (wavelength emitted by atomic hydrogen in interstellar space).
(b) 1057 MHz (frequency of radiation arising from two close energy levels in hydrogen; known as Lamb shift).
(c) 2.7 K (temperature associated with the isotropic radiation filling all space-thought to be a relic of ‘big-bang’ origin of the universe).
(d) 5890 Å - 5896 Å [double lines of radius]
(e) 14.4 keV [energy of a particular transition in 57 Fe nucleus associated with a famous high-resolution spectroscopic method (Mossbauer spectroscopy)]
Answer:
(a) 21 cm wavelength belongs to radio waves region of e.m. spectrum.
(b) v = 1057 MHz belongs to radio waves region of e.m. spectrum because
λ = \(\frac{c}{v}=\frac{3 \times 10^8}{1.057 \times 10^9}\)
= 28.3 cm

(c) From Wien’s displacement law,
λ_m = \(\frac{0.29}{\mathrm{~T}}=\frac{0.29}{2.7}\) = 0.11 cm.
So 0.11 cm wavelength belongs to microwave region of e.m. spectrum.
(d) 5890 Å - 5896 Å belongs to visible region of e.m. spectrum.
(e) E = 14.4 keV = 14.4 x 10³ eV
So λ = \(\frac{12400}{\mathrm{E}(\text { in } e \mathrm{~V})}=\frac{12400}{14.4 \times 10^3}\)
= 0.7 A.
This wavelength belongs to X-ray region of e.m. spectrum.

Question 8.16.
Answer the following questions:
(a) Long-distance radio broadcasts use short-wave bands. Why?
(b) It is necessary to use satellites for long-distance TV transmission. Why?
(c) Optical and radio telescopes are built on the ground but X-ray astronomy is possible only from satellites orbiting the earth. Why?
(d) The small ozone layer on top of the stratosphere is crucial for human survival. Why?
(e) If the earth did not have an atmosphere, would its average surface temperature be higher or lower than what it is now?
(f) Some scientists have predicted that a global nuclear war on the earth would be followed by severe nuclear winter with a devastating effect on life on earth. What might be the basis of this prediction?
Answer:
(a) Short waves having range 1500 kHz to 30 mHz are easily reflected by ionosphere, hence long distance radio broadcasts use short wave bands.

(b) Because T.V. signals being of high frequency are not reflected by ionosphere so they are superimposed on microwaves and are sent towards the satellite and are transmitted in various directions from the satellite.

(c) Our atmosphere is more or less transparent to optical and radio frequencies hence ground telescopes are optical and radio telescopes. But X-rays emitted from astronomical objects are absorbed in the atmosphere around the earth and cannot reach the earth, so X-ray astronomical objects are absorbed in the atmosphere around the earth and cannot reach the earth’s, so X-ray astronomical telescopes must be used on the satellite orbiting above the earth’s atmosphere.

(d) Because ultraviolet radiation (which is very harmful for living cells and plants and hence human life) coming from the sun gets absorbed by the ozone layer.

(e) The temperature of the earth would be lower because the greenhouse effect of the atmosphere would be absent.

(f) Due to global nuclear war on the earth, the atmosphere will be covered or clouded with ‘nuclear dust’. In the peculiar situation, solar radiation will be completely prevented from reaching the earth. Hence the temperature of earth will sufficiently fall down. Scientists call this situation a ‘nuclear winter’ on earth. 

SELECTED EXEMPLAR PROBLEMS

MCQ I [with one correct option]

Question 8.1.
One requires 11 eV of energy to dissociate a carbon monoxide molecule into carbon and oxygen atom. The minimum frequency of the appropriate electromagnetic radiation to achieve the dissociation lies in
(a) visible region
(b) infrared region
(c) ultraviolet region
(d) microwave region.
Answer:
(c) E = 11eV = 11 x 1.6 x 10^-19 J
and v = \(\frac{\mathrm{E}}{h}=\frac{11 \times 1.6 \times 10^{-19}}{6.62 \times 10^{-34}}\) = 2.65 x 10¹⁵ Hz
This frequency radiation belongs to ultraviolet region.

Question 8.2.
Light with an energy flux of 20 W/cm² falls on a non-reflecting surface at normal incidence. If the surface has an area of 30 cm², the total momentum delivered (for complete absorption) during 30 minutes is:
(а) 36 x 10^-5 kg m/s
(b) 36 x 10^-4 kg m/s
(c) 108 x 10⁴ kg m/s
(d) 1.08 x 10⁷ kg m/s.
Answer:
(b). Total energy falling on the surface in time t.
U = φ At = 20 x 30 x 30 x 60 J
Momentum of incident light pi = \(\frac{\mathrm{U}}{\mathrm{c}}\)
or pi = \(\frac{20 \times 30 \times 30 \times 60}{3 \times 10^6}\) = 36 x 10^-4 kg ms^-1
Momentum of reflected light pr = 0
Momentum delivered to the surface = 36 x 10^-4 - 0 = 36 x 10^-4 kg ms^-1.

Question 8.3.
If E and B represent electric and magnetic field vectors of the electromagnetic wave the direction of propagation of electromagnetic wave is along
(a) \(\overrightarrow{\mathbf{E}}\)
(b) \(\overrightarrow{\mathbf{B}}\)
(c) \(\overrightarrow{\mathbf{B}}\) x \(\overrightarrow{\mathbf{E}}\)
(d) \(\overrightarrow{\mathbf{E}}\) x \(\overrightarrow{\mathbf{B}}\).
Answer:
(d). The direction of propagation of e.m. wave is perpendicular to both \(\overrightarrow{\mathbf{E}}\) x \(\overrightarrow{\mathbf{B}}\).

Question 8.4.
The ratio of contributions made by the electric field and magnetic field components to the intensity of an EM wave is:
(a) c : 1
(b) c² : 1
(c) 1 : 1
(d) \(\sqrt{c}\) : 1
Answer:
(c) The energy in electromagnetic waves is divided equally between electric field vectors and magnetic field vectors.

Question 8.5. 
An EM wave radiates out waves from a dipole antenna, with E₀ as the amplitude of its electric field vector. The electric field E0 which transports significant energy from the source falls off as:
(a) \(\frac{1}{r^3}\)
(b) \(\frac{1}{r^2}\)
(c) \(\frac{1}{r}\)
(d) remains constant.
Answer:
(c) E₀ ∝ \(\frac{1}{r}\).

MCQ II. [with more than one correct option]

Question 8.6.
An electromagnetic wave travels in vacuum along z direction : \(\overrightarrow{\mathbf{E}}=\left(\mathbf{E}_1 \hat{i}+\mathbf{E}_2 \hat{j}\right)\) cos (kz - ωt). Choose the correct options from the following:
(a) The associated magnetic field is given as
\(\overrightarrow{\mathrm{B}}=\frac{1}{c}\left(\mathrm{E}_1 \hat{i}-\mathrm{E}_2 \hat{j}\right) \cos (k z-\omega t)\)
(b) The associated magnetic field is given as
\(\overrightarrow{\mathbf{B}}=\frac{1}{c} \quad\left(\mathbf{E}_1 \hat{i}-E_2 \hat{j}\right) \cos (k z-\omega t)\)
(c) The given electromagnetic field is circularly polarised.
(d) The given electromagnetic wave is plane polarised.
Answer:
(a), (d)
E = \( \left(\mathrm{E}_1 \hat{i}-\mathrm{E}_2 \hat{j}\right) \cos (k z-\omega t)\)
And B = \(\frac{\mathrm{E}}{c}=\frac{1}{c}\left(\mathrm{E}_1 \hat{i}+\mathrm{E}_2 \hat{j}\right) \cos (k z+\omega t)\)
\(\overrightarrow{\mathbf{E}}\) and \(\overrightarrow{\mathbf{B}}\) are perpendicular to each other and direction of motion of e.m. wave is to ⊥ both \(\overrightarrow{\mathbf{E}}\) and \(\overrightarrow{\mathbf{B}}\).

Question 8.7.
An electromagnetic wave traveling along z-axis is given as E = E₀ cos (kz - ωt). Choose the correct options from the following:
(a) The associated magnetic field is given as
\(\overrightarrow{\mathbf{B}}=\frac{1}{\mathrm{c}} \hat{\boldsymbol{k}} \times \overrightarrow{\mathrm{E}}=\frac{1}{\omega}(\hat{\boldsymbol{k}} \times \overrightarrow{\mathrm{E}})\)
(b) The electromagnetic field can be written in terms of the associated magnetic field as
\(\overrightarrow{\mathbf{E}}=\mathrm{c}(\overrightarrow{\mathrm{B}} \times \hat{k})\)
(c) \(\hat{k} \cdot \overrightarrow{\mathrm{E}}=0 \hat{k} \cdot \overrightarrow{\mathrm{B}}=0\)
(d) \(\hat{k} \times \overrightarrow{\mathrm{E}}=0, \hat{k} \times \overrightarrow{\mathrm{B}}=0.\) 
Answer:
(a), (b), (c)
In e.m. wave, B₀ = \(\frac{\mathrm{E}_0}{\mathrm{c}}\)
Associated electric field can be written in terms of magnetic field

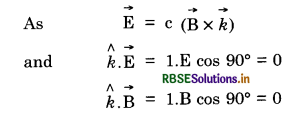
Question 8.8.
A plane electromagnetic wave propagating along x direction can have the following pairs of E and B:
(a) E_x.B_y
(b) E_y.B_z
(c) B_x.E_y
(d) E_z.B_y
Answer:
(b), (d), Because electric and magnetic field vectors \(\overrightarrow{\mathrm{E}}\) and \(\overrightarrow{\mathrm{B}}\) all ⊥ to each other and also ⊥ to the direction of propagation of the wave.

Question 8.9.
A charged particle oscillates about its mean equilibrium position with a frequency of 10⁹ Hz. The electromagnetic waves produced:
(a) will have a frequency of 10⁹ Hz
(b) will have a frequency of 2 x 10⁹ Hz
(c) will have a wavelength of 0.3 m
(d) fall in the region of radiowaves.
Answer:
(a), (c), (d)
Given v = 10⁹ Hz
So λ =\( \frac{c}{v}=\frac{3 \times 10^8}{10^9}\) = 0.3 m
Frequency 10⁹ Hz belongs to radiowaves region.

Question 8.10.
The source of electromagnetic waves can be a charge
(a) moving with a constant velocity
(b) moving in a circular orbit
(c) at rest
(d) falling in an electric field.
Answer:
(b), (d) electromagnetic waves can be produced by accelerating charged particles which may be moving in a circular orbit or falling in an electric field.

Question 8.11.
An EM wave of intensity I falls on a surface kept in a vacuum and exerts radiation pressure p on it. Which of the following is true?
(a) Radiation pressure is I/c if the wave is totally absorbed
(b) Radiation pressure is I/c if the wave is totally reflected
(c) Radiation pressure is 2I/p if the wave is totally reflected
(d) Radiation pressure is in the range I/c < p < 2I/c for real surfaces.
Answer:
(a), (c), (d)
Radiation pressure is force exerted per unit area by em wave i.e. rate of change of momentum.
Momentum per unit time per unit area = \(\frac{\mathrm{I}}{c}\)
Radiation pressure (p) = change in momentum per unit time per unit area = \(\frac{\Delta \mathrm{I}}{c}\)
When wave is totally absorbed
Radiation pressure p = \(\frac{\Delta \mathrm{I}}{c}=\frac{\mathrm{I}}{c}-0=\frac{\mathrm{I}}{c}\)
When wave is totally reflected
p =\(\frac{\Delta \mathrm{I}}{c}=\frac{\mathrm{I}}{c}-\left(-\frac{\mathrm{I}}{c}\right)=\frac{2 \mathrm{I}}{c}\)
Here p, lies between \(\frac{\mathrm{I}}{c} and \frac{\mathrm{2I}}{c}\).

Very Short Answer Type Questions

Question 8.12.
Why is the orientation of the portable radio with respect to broadcasting stations important?
Answer:
Transmitted e.m. waves are plane polarised, so the receiving antenna should be parallel to the electric or magnetic field of the wave. 

Question 8.13.
Why does a microwave oven heat up a food item containing water molecules most efficiently?
Answer:
Frequency of microwaves matches the resonant frequency of water molecules.

Question 8.14.
The charge on a parallel plate capacitor varies as q = q₀ cos 2πvt. The plates are very large and close together (area = A, separation = d). Neglecting the edge effects, find the displacement current through the capacitor?
Answer:
Displacement current
I_D = I_C = \(\frac{d q}{d t}=\frac{d}{d t}\)(q₀ cos 2πvt) = -q₀ 2πv sin 2πvt

Question 8.15.
A variable frequency a.c. source is connected to a capacitor. How will the displacement current change with decrease in frequency?
Answer:
I = \(\frac{\mathrm{E}}{\mathrm{X}_{\mathrm{C}}}=\frac{\mathrm{E}}{\frac{1}{2 \pi v \mathrm{C}}}\)
or I ∝ v
As v decreases, the conduction current also decreases, So, the displacement current also decreases.

Question 8.16.
The magnetic field of a beam emerging from a filter facing a floodlight is given by
B₀ = 12 x 10^-8 sin (1.20 x 10⁷ z - 3.60 x 10¹⁵ t) T.
What is the average intensity of the beam?
Answer:
I_av = \(\frac{c}{2} \frac{\mathrm{B}_0^2}{\mu_0^2}=\frac{3 \times 10^8 \times\left(12 \times 10^{-8}\right)^2}{2 \times 4 \pi \times 10^{-7}}\) = 1.7 Wm^-2

Question 8.17.
Poynting vector S is defined as a vector whose magnitude is equal to the wave intensity and whose direction is along the direction of wave propagation. Mathematically, it is given by \(\overrightarrow{\mathrm{S}}=\frac{1}{\mu_0} \overrightarrow{\mathbf{E}} \times \overrightarrow{\mathbf{B}}\). Show the nature of S vs t graph.
Answer:
An e.m. wave moving along X-axis has \(\overrightarrow{\mathrm{E}}\) along y-axis and \(\overrightarrow{\mathrm{B}}\) along z-axis.
Let \(\overrightarrow{\mathrm{E}}\) = E₀ sin (ωt - kx) \(\hat{j}\)
\(\overrightarrow{\mathrm{B}}\) = B₀ sin (ωt - kx) \hat{k}
So \(\overrightarrow{\mathrm{S}}=\overrightarrow{\mathrm{E}} \times \overrightarrow{\mathrm{B}}\)= E₀B₀ sin² (ωt - kx) (\(\hat{j}\) x \(\hat{k}\))
or \(\overrightarrow{\mathrm{S}}=\mathrm{E}_0 \mathrm{~B}_0 \sin ^2(\omega \mathrm{t}-k x) \hat{i}\)

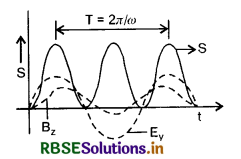
Variation of S with time is shown in Fig. EP 8.3.

Question 8.18.
Professor C. V. Raman surprised his students by suspending freely a tiny light ball in a transparent vacuum chamber by shining a laser beam on it. Which property of EM waves was he exhibiting? Give one more example of this property.
Answer:
Electromagnetic waves exert radiation pressure. The tails of comets are due to radiation pressure.

Short Answer Type Questions

Question 8.19.
Show that the magnetic field B at a point in between the plates of a parallel-plate capacitor during charging is \(\frac{\varepsilon_0 \mu_{\mathbf{r}}}{2} \frac{\mathbf{d E}}{\mathbf{d t}}\) (symbols having usual meanings.)
Answer:
Magnetic field between the plates of a parallel (-) plate capacitor at a distance r from the axis of the plates is given by

Question 8.20.
Electromagnetic waves with wave-length
(i) λ₁ is used in satellite communication.
(ii) λ₂ is used to kill germs in water purifiers.
(iii) λ₃ is used to detect leakage of oil in underground pipelines.
(iv) λ₄ is used to improve visibility in runways during fog and mist conditions.
(a) Identify and name the part of electromagnetic spectrum to which these radiations belong.
(b) Arrange these wavelengths in ascending order of their magnitude.
(c) Write one more application of each.
Answer:
(a) λ₁ → Microwave, λ₂ → UV, λ₃ → X-rays, λ₄ → Infrared
(b) λ₃ < λ₂ < λ₄ < λ₁
(c) Microwaves → Radar, UV → LASIK eye surgery, X-rays → Bone fracture identification (bone scanning), I.R. → optical communication.

Question 8.21.
You are given a 2 µF parallel capacitor. How would you establish an instantaneous displacement current of 1mA in the space between its plates?
Answer:
Since q = CV
∴ I_D dt = C dV
or \(\frac{d \mathrm{~V}}{d t}=\frac{\mathrm{I}_{\mathrm{D}}}{\mathrm{C}}=\frac{10^{-3}}{2 \times 10^{-6}}\) = 500 Vs^-1
So when a varying potential difference of 500 Vs^-1 is applied the desired displacement current is produced.

Question 8.22.
Show that the radiation pressure exerted by an EM wave of intensity I on a surface kept in vaccum is I/c.
Answer:
Pressure, P = \(\frac{\mathrm{F}}{\mathrm{A}}=\frac{1}{\mathrm{~A}} \frac{\Delta p}{\Delta t}\) ...................(i)
[\(\frac{\Delta p}{\Delta t}\) is rate of change of momentum]
Since energy imparted by wave in time ∆t is given to by
∆U = ∆p c
or ∆p = \(\frac{\Delta \mathrm{U}}{\mathrm{c}}\)
So eqn. (i) becomes
p = \(\frac{1}{\mathrm{~A}} \frac{\mathrm{U}}{\Delta t \cdot \mathrm{c}}\)
or p = \(\frac{\mathrm{I}}{\mathrm{c}}\) [∵ I = \(\frac{\mathrm{U}}{\mathrm{A} \Delta t}\)]

Question 8.23.
What happens to the intensity of light from a bulb if the distance from the bulb is doubled? As a laser beam travels across the length of a room, its intensity essentially remains constant.
What geometrical characteristic of LASER beam is responsible for the constant intensity which is missing in the case of light from the bulb?
Answer:
Intensity is reduced to one-fourth. This is because the light beam spreads, as it propagates into a spherical region of area 4πr² i.e. I ∝ \(\frac{1}{r^2}\). But LASER does not spread and hence its intensity remains constant.

Question 8.24.
Even though an electric field E exerts a force qE on a charged particle yet the electric field of an EM wave does not contribute to the radiation pressure (but transfers energy). Explain.
Answer:
Since electric field of an e.m. wave is oscillating, so electric force on e.m. wave is also oscillating. The average value of electric force over a complete cycle is zero. Hence electric field is not responsible for radiation pressure.

Long Answer Type Questions

Question 8.25.
An infinitely long thin wire carrying a uniform linear static charge density λ is placed along the z-axis [Fig. EP 8.28]. The wire is set into motion along its length with a uniform velocity \(\vec{v}=v \hat{\boldsymbol{k}_z}\). Calculate the poynting vector \(\overrightarrow{\mathrm{S}}=\frac{1}{\mu_0}(\overrightarrow{\mathrm{E}} \times \overrightarrow{\mathrm{B}})\).

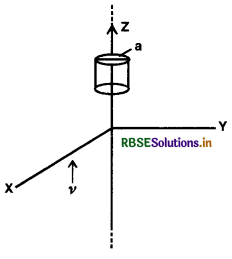
Answer:
Electric field due to wire at a distance a is \(\overrightarrow{\mathrm{E}}=\frac{1}{2 \pi \varepsilon_0} \frac{\lambda}{a} \hat{j}\)
Magnetic field at distance a from an infinitely long current-carrying wire is

Question 8.26.
Sea water at frequency v = 4 x 10⁸ Hz has permittivity ε ≈ 80 ε₀, permeability µ = µ₀ and resistivity p = 0.25 Ω-m. Imagine a parallel plate capacitor immersed in seawater and driven by an alternating voltage source V(t) = V₀ sin (2πvt). What fraction of the conduction current density is the displacement current density?
Answer:
Let d be the distance between the plates of the capacitor.
Applied electric field E = \(\frac{\mathrm{V}(t)}{d}=\frac{\mathrm{V}_0}{d}\) sin (2πvt)
The current density 
J_C = \(\frac{E}{\rho}=\frac{V_0}{\rho d}\)sin 2πλt = J_OC sin 2πvt
where J_OC = \(\frac{\mathrm{V}_0}{\rho d}\) is max. condition current density. The displacement current
J_D = \(\frac{\mathrm{I}_{\mathrm{D}}}{\mathrm{A}}=\frac{\varepsilon_0 \varepsilon_r}{\mathrm{~A}} \frac{d \phi_e}{d t}=\varepsilon_0 \varepsilon_r \frac{d \mathrm{E}}{d t}\) [∵ Φ_e = AE]
= ε₀ ε_r \(\frac{d}{d t}\left[\frac{\mathrm{V}_0}{d} \sin (2 \pi v t)\right]\)
= ε₀ ε_r \(\frac{\mathrm{V}_0}{d}\) 2πr cos 2πvt
= J_OD cos 2πvt
where J_OD = \(\frac{2 \pi v \varepsilon_0 \varepsilon_r \mathrm{~V}_0}{d}\) is max. displacement current density

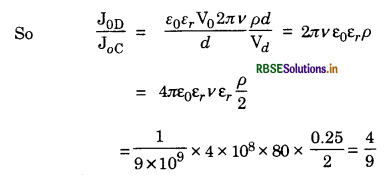
Question 8.27.
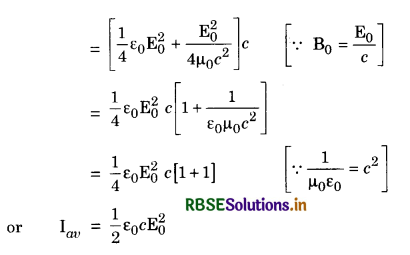
A plane EM wave traveling along z direction is described by\( \overrightarrow{\mathbf{E}}\) = E₀ sin (kz - ωt) \(\overrightarrow{\mathbf{i}}\) and \(\overrightarrow{\mathbf{B}}\) = B₀ sin (kz - ωt) \(\overrightarrow{\mathbf{j}}\). Show that
(i) The average energy density of the wave is given by
U_av = \(\frac{1}{4} \varepsilon_0 \mathrm{E}_0^2+\frac{1}{4} \frac{\mathrm{B}_0^2}{\mu_0}\).
(ii) The time-averaged intensity of the wave is given by
I_av = \(\frac{1}{2}\)cε₀E₀².
Answer:
(i) We know that Electric energy density
U_E = \(\frac{1}{2}\)ε₀E².
and magnetic energy density
U_B = \(\frac{1}{2}\frac{\mathrm{B}^2}{\mu_0}.\)
Total average energy density
U_av = U_E + U_B = \(\frac{1}{2}\)ε₀E² + \(\frac{1}{2}\frac{\mathrm{B}^2}{\mu_0}\) ....................(i)
Given E = E₀ sin (kz - ωt)
B = B₀ sin (kz - ωt)
Time average value of E² over complete cycle = \(\frac{\mathrm{E}_0^2}{2}\)
and time average value of B² over complete cycle = \(\frac{\mathrm{B}_0^2}{2}\)
∴ U_av = \(\frac{1}{2} \varepsilon_0 \frac{\mathrm{E}_0^2}{2}+\frac{1}{2} \mu_0 \frac{\mathrm{B}_0^2}{2}=\frac{1}{4} \varepsilon_0 \mathrm{E}_0^2+\frac{\mathrm{B}_0^2}{4 \mu_0}\)

(ii) Average intensity
I_av = U_av c = \(\left[\frac{1}{4} \varepsilon_0 \mathrm{E}_0^2+\frac{\mathrm{B}_0^2}{4 \mu_0}\right]\) c