RBSE Solutions for Class 12 Physics Chapter 7 प्रत्यावर्ती धारा

Rajasthan Board RBSE Solutions for Class 12 Physics Chapter 7 प्रत्यावर्ती धारा Textbook Exercise Questions and Answers.

RBSE Class 12 Physics Solutions Chapter 7 प्रत्यावर्ती धारा

RBSE Class 12 Physics प्रत्यावर्ती धारा Textbook Questions and Answers

प्रश्न 1.
एक 100Ω का प्रतिरोधक 200 V, 50 Hz  आपूर्ति से संयोजित है।
(a) परिपथ में धारा का rms मान कितना है?
(b) एक पूरे चक्र में कितनी नेट शक्ति व्यय (power consumed) होती है? 
हल: 
(a) दिया है: R = 100Ω; V_rms = 200 V; f = 50 Hz, I_rms = ?
∴ परिपथ में धारा का वर्ग माध्य मूल मान
\(I_{r m s}=\frac{V_{r m s}}{R}=\frac{200}{100}=2.0 \mathrm{~A}\)

(b) ∵ परिपथ में केवल शुद्ध प्रतिरोध है अत:
\(\phi=0 \therefore \cos \phi=1 \)
अतः शक्ति व्यय
P = V_rms .I_rms.cosΦ
= V_rms.I_rms
= 200 x 2.0
= 400 वाट 

प्रश्न 2. 
(a) AC आपूर्ति (a.c. supply) का शिखर मान (peak value) 300 V है; rms वोल्टता कितनी होगी?
(b) AC - परिपथ में धारा का rms मान 10 A है; शिखर धारा कितनी होगी? 
हल: 
(a) दिया है: V_m = 300 V;V_rms = ?
I_rms = 10 A; I₀ = ?
\(\begin{aligned} &\because \quad \mathrm{V}_{r m s}=\frac{\mathrm{V}_m}{\sqrt{2}}\\ &\therefore \quad \mathrm{V}_{m s}=\frac{300}{\sqrt{2}}=\frac{300}{1.414}\\ &=212.16 \mathrm{~V}=\mathbf{2 1 2 \cdot 1} \mathrm{V} \end{aligned}\)

(b) \(\because \quad \mathrm{I}_{r m s}=\frac{I_m}{\sqrt{2}} \Rightarrow \mathrm{I}_m=\mathrm{I}_{r m s} \cdot \sqrt{2}\)
\(\therefore \quad \mathrm{I}_m=10 \times 1.414=\mathbf{1 4 . 1 4} \mathbf{A}\)

प्रश्न 3.
एक 44 mH का प्रेरक (induction) 220 V, 50 Hz आपूर्ति से जोड़ा गया है। परिपथ में धारा का rms मान ज्ञात कीजिए। 
हल: 
दिया है: L = 44 mH = 44 x 10^-3 H; V_rms = 220 V; f = 50 Hz; I_rms = ?
प्रेरक का प्रेरणिक प्रतिघात
X = 2πfL 
= 2 x 3.14 x 50 x 44 x 10^-3
= 13816 x 10^-3 = 13.816Ω
= 13.82Ω 
∴ धारा का वर्ग माध्य मूल मान
\(\begin{aligned} \mathrm{I}_{r m s} &=\frac{\mathrm{V}_{r m s}}{\mathrm{X}_{\mathrm{L}}}=\frac{220}{13.82} \\ &=15.918=15.92 \mathrm{~A} \end{aligned}\)

प्रश्न 4.
एक 60 µF का संधारित्र 110 V,60 Hz की AC आपूर्ति से जुड़ा है। परिपथ में धारा का rms मान ज्ञात कीजिए।
हल:
दिया है: C = 60 µF = 60 x 10^-6 F = 6 x 10^-5 F; V_rms = 110 V; f = 60 Hz; I_rms = ?
संधारित्र का धारितीय प्रतिघात

∴ परिपथ में धारा का वर्ग माध्य मूल मान
\(\begin{aligned} \mathrm{I}_{r m s} &=\frac{\mathrm{V}_{r m s}}{\mathrm{X}_{\mathrm{C}}}=\frac{110}{44.23} \\ &=2.4869=\mathbf{2 . 4 9 \mathrm { A }} \end{aligned}\)

प्रश्न 5. 
प्रश्न 3 व 4 में एक पूरे चक्र की अवधि में प्रत्येक परिपथ में कितनी नेट शक्ति अवशोषित (net power absorbed) होती है? अपने उत्तर का विवरण दीजिए।
हल: 
प्रश्न 3 व 4 दोनों में पूरे चक्र के लिए नेट अवशोषित शक्ति शून्य होगी। 
विवरण: ∵ P = V_rms .I_rms .cos\(\phi\)
और प्रेरकत्व तथा संधारित्र दोनों के लिए
\(\phi=\pi / 2 \therefore \cos \phi=0\)
अतः P = 0

प्रश्न 6. 
एक LCR परिपथ की, जिसमें L = 2.0 H, C = 32 µF एवं R = 10Ω; अनुनाद आवृत्ति (resonant frequency) \(\omega_r\) का परिकलन कीजिए। इस परिपथ के लिए Q - गुणक का मान क्या होगा?
हल: 
दिया है: L = 2.0 H; C = 32 µF = 32 x 10^-6 F; R = 10Ω;\( \omega_r\) = ?; Q = ?
परिपथ की अनुनादी कोणीय आवृत्ति (resonant angular frequency)

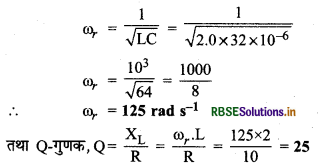
प्रश्न 7.
30 µF का आवेशित संधारित्र 27 mH के प्रेरिन से जोड़ा गया है। परिपथ के मुक्त दोलनों (free oscillation) की कोणीय आवृत्ति (angular frequency) कितनी है?
हल: 
दिया है: C = 30µF = 30 x 10^-6 F = 3 x 10^-5 F; L = 27 x 10^-3 H; \(\omega_r\) = ?

प्रश्न 8. 
कल्पना कीजिए कि प्रश्न 7 में संधारित्र पर प्रारम्भिक आवेश (Initial charge) 6 mC है। प्रारम्भ में परिपथ में कुल कितनी ऊर्जा संचित (stored) होती है। बाद में कुल ऊर्जा कितनी होगी?
हल: 
दिया है: C = 30 µF = 30 x 10^-6 F = 3 x 10^-5 F; Q0 = 6 x 10^-3 C 
∴ प्रारम्भ में परिपथ में संचित ऊर्जा
E =  संधारित्र की ऊर्जा + प्रेरित्र की ऊर्जा
\(=\frac{1}{2} \frac{\mathrm{Q}_0{ }^2}{\mathrm{C}}+\frac{1}{2} \mathrm{~L} i_0^2\)
प्रारम्भ में i₀ = 0
∴ E=\(\frac{1}{2} \frac{\mathrm{Q}_0^2}{\mathrm{C}}=\frac{1}{2} \times \frac{6 \times 10^{-3} \times 6 \times 10^{-3}}{3 \times 10^{-5}}\)
= 6 x 10^-1 = 0.6 J
∵ परिपथ में कोई प्रतिरोध नहीं जुड़ा है और शुद्ध प्रेरकत्व या शुद्ध संधारित्र के लिए P = 0, क्योंकि दोनों के लिए \(\phi=\pi / 2 \therefore \cos \phi=0\)
अत: बाद में भी परिपथ में ऊर्जा = प्रारम्भिक ऊर्जा = 0.6 J

प्रश्न 9. 
एक श्रेणीबद्ध LCR परिपथ को, जिसमें R = 20Ω,L = 1.5 H, तथा C = 35 µF, एक परिवर्ती आवृत्ति (variable frequency) की 200 V AC आपूर्ति से जोड़ा गया है। जब आपूर्ति की आवृत्ति परिपथ की मूल आवृत्ति (natural frequency) के बराबर होती है तो एक पूरे चक्र में परिपथ को स्थानान्तरित की गई माध्य शक्ति कितनी होगी?
हल: 
दिया है: R = 20Ω; L = 1.5 H; C = 35 µF = 35 x 10^-6 F; V_rms = 200 V,
जब परिपथ की मूल आवृत्ति आपूर्ति (supply) की आवृत्ति के बराबर होगी तो अनुनाद (resonance) की स्थिति होगी और अनुनाद की स्थिति में,
Z = R = 20Ω 
∴परिपथ में धारा
\(\mathrm{I}_{r m s}=\frac{\mathrm{V}_{r m s}}{\mathrm{Z}}=\frac{\mathrm{V}_{r m s}}{\mathrm{R}}=\frac{200}{20}=10 \mathrm{~A}\) 
अनुनाद की स्थिति में \(\phi=0\)
\(\therefore \quad \cos \phi=\cos 0^{\circ}=1\)
∴ पूरे चक्र में परिपथ को स्थानान्तरित शक्ति (transferred power)
\(\begin{aligned} \mathrm{P} &=\mathrm{V}_{r m s} \times \mathrm{I}_{r m s} \times \cos \phi \\ &=200 \times 10 \times 1 \end{aligned}\)
= 2000 वाट (broadcast band)

प्रश्न 10. 
एक रेडियो को MW प्रसारण बैण्ड के एक खण्ड (portion) के आवृत्ति परास के एक ओर से दूसरी ओर (800 KHz से 1200 KHz) तक समस्वरित (tune) किया जा सकता है। यदि इसके LC परिपथ का प्रभावकारी प्रेरकत्व 200 µH हो तो उसके परिवर्ती संधारित्र की परास कितनी होनी चाहिए। 
हल: 
दिया है: प्रसारण बैण्ड की आवृत्ति
f = 800 kHz - 1200kHz
∴ f_min = 800 kHz = 800 x 10³ = 8 x 10⁵ Hz
f_max = 1200 kHz = 1200 x 10³ = 12 x 10⁵ Hz
L = 200 µH = 200 x 10^-6 H = 2 x 10^-4 H
रेडियो को प्रसारण बैण्ड के साथ समस्वरित करने के लिए LC परिपथ की मूल आवृत्ति प्रसारण की आवृत्ति के बराबर होनी चाहिए। 
∵ LC परिपथ की मूल आवृत्ति अर्थात् अनुनादी आवृत्ति
\(f_0=\frac{1}{2 \pi \sqrt{\mathrm{LC}}}\) या \(f_0^2=\frac{1}{4 \pi^2 \mathrm{LC}}\)
∴ \(\mathrm{C}=\frac{1}{4 \pi^2 \mathrm{~L} \cdot f_0^2}\)
∴ जब f₀ = f_min = 8 x 10⁵ H
∴ जब आवृत्ति न्यूनतम होगी तो संधारित्र की धारिता अधिकतम होगी,

अतः परिवर्ती संधारित्र की परास 88 pF से 198 pF तक होनी चाहिए।

प्रश्न 11. 
चित्र में एक श्रेणीबद्ध LCR परिपथ दिखलाया गया है जिसे परिवी आवृत्ति के 230 V के स्रोत से जोड़ा गया है। L = 5.0 H; C = 80 µF, R = 40Ω.

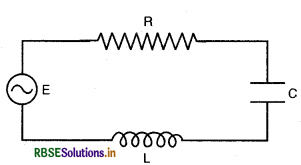
(a) स्रोत की आवृत्ति (source frequency) निकालिए जो परिपथ में अनुनाद (resonance) उत्पन्न करे।
(b) परिपथ की प्रतिबाधा तथा अनुनादी आवृत्ति पर धारा का आयाम निकालिए।
(c) परिपथ के तीनों अवयवों के सिरों पर विभवपात (potential drop) के rms मानों को निकालिए। दिखलाइए कि अनुनादी आवृत्ति पर LC संयोग के सिरों पर विभवपात शून्य है।
हल: 
दिया है: L = 5.0 H; C = 80 µF = 80 x 10^-6 F; R = 40Ω; V_rms = 230 V. 
(a) अनुनाद के लिए स्रोत की कोणीय आवृत्ति

(b) ∵ अनुनाद की स्थिति में,
X_L = X_C  ∴X = X_L ~ X_C = 0
∴ परिपथ की प्रतिबाधा 
\(\begin{aligned} Z &=\sqrt{\mathrm{R}^2+X^2} \\ &=\sqrt{\mathrm{R}^2+0}=\mathrm{R}=40 \Omega \end{aligned}\)
धारा का वर्ग माध्य मूल मान
\(I_{r m s}=\frac{V_{r m s}}{Z}=\frac{230}{40}=5.75 \mathbf{A}\)
\(\begin{aligned} \because & \mathrm{I}_{r m s} &=\frac{\mathrm{I}_0}{\sqrt{2}} \Rightarrow \mathrm{I}_0=\mathrm{I}_{r m s} \sqrt{2} \\ \therefore & \mathrm{I}_0 &=5.75 \times 1.414=\mathbf{8 . 1 3} \mathbf{A} \end{aligned}\)

(c)∵ X_L = \(\omega \mathrm{L}=\omega_r \mathrm{~L}=50 \times 5.0=250 \Omega\)
और \(X_C=X_L=250 \Omega\)
अतः प्रतिरोध के सिरों पर विभवान्तर का ms मान
(V_R)_rms = I_rms .R = 5.75 x 40 = 230 V 
प्रेरकत्व के लिए (V_L)_rms = I_rms x X_L
= 5.75 x 250 = 1437.5 V 
संधारित्र के लिए (V_C)_rms = I_rms x X_C
= 5.75 x 250 = 1437.5 V

प्रश्न 12.
किसी LC परिपथ में 20 mH का एक प्रेरकत्व (Inductor) तथा 50 µF का संधारित्र है जिस पर प्रारम्भिक आवेश 10 mC है। परिपथ का प्रतिरोध नगण्य है। मान लीजिए कि वह क्षण जिस पर परिपथ बन्द किया जाता है t = 0 है।
(a) प्रारम्भ में कुल कितनी ऊर्जा संचित (stored initially) है? क्या यह L.C दोलनों की अवधि में संरक्षित (conserved) है?
(b) परिपथ की मूल आवृत्ति क्या है?
(c) किस समय पर संचित ऊर्जा (stored energy) (i) पूर्णत: वैद्युत है (अर्थात् वह संधारित्र में संचित है)। (ii) पूर्णतः चुम्बकीय है (अर्थात् वह प्रेरक में संचित है)।
(d) किन समयों पर (at what times) कुल ऊर्जा प्रेरित तथा संधारित्र में समान रूप से विभाजित है।
(e) यदि एक प्रतिरोधक को परिपथ में लगाया जाये (Inserted), तो कितनी ऊर्जा अन्तत: ऊष्मा के रूप में क्षयित होगी (eventually dissipated as heat)?
हल: 
दिया है: L = 20 mH = 20 x 10^-3 H; C = 50 µF = 50 x 10^-6 F;q₀ = 10 mC = 10 x 10^-3 C.
(a) प्रारम्भ में कुल संचित ऊर्जा,
\(\mathrm{U}_i=\frac{q_0^2}{2 \mathrm{C}}=\frac{\left(10 \times 10^{-3}\right)^2}{2 \times 50 \times 10^{-6}}=\frac{100 \times 10^{-6}}{100 \times 10^{-6}}=\mathbf{1 . 0 J}\)
हाँ, कुल ऊर्जा L - C दोलनों की अवधि में संरक्षित (conserved) है (क्योंकि परिपथ ओमीय प्रतिरोध से मुक्त है।)

(b) परिपथ की मूल आवृत्ति अर्थात् अनुनादी कोणीय आवृत्ति 
\(\begin{aligned} \omega=\frac{1}{\sqrt{\mathrm{LC}}} &=\frac{1}{\sqrt{20 \times 10^{-3} \times 50 \times 10^{-6}}} \\ &=\frac{1}{10^{-3}}=10^3 \text { rad } \mathrm{s}^{-1} \end{aligned}\)

(c) जब परिपथ t = 0 पर बन्द किया जाता है, तो संधारित्र के आवेशन का समीकरण है,
\(q=q_0 \cos \omega t\)

(i) ऊर्जा पूर्णत: वैद्युत (completely electrical) है यदि q = q₀ अर्थात् \(cos \omega t = 1\)
या \(\omega t=0, \pi, 2 \pi, 3 \pi, 4 \pi, \ldots ., n \pi \)
अर्थात् \(\omega t=n \pi\)
यहाँ n = 0, 1, 2, 3, 4,........
∴ \(t=\frac{n \pi}{\omega}=\frac{n \pi}{\frac{2 \pi}{\mathrm{T}}}=\frac{n \mathrm{~T}}{2}\)
या t = 0, \(\frac{\mathrm{T}}{2}, \mathrm{~T}, \frac{3 \mathrm{~T}}{2}, 2 \mathrm{~T}, \).........

(ii) परिपथ की ऊर्जा पूर्णतः चुम्बकीय (completely magnetic) है, जब वैद्युत ऊर्जा शून्य है अर्थात्
q = 0 जो तभी सम्भव है जब 
\(\cos \omega t=0\)
या \(\omega t=\frac{\pi}{2}, \frac{3 \pi}{2}, \frac{5 \pi}{2}, \frac{7 \pi}{2}, \ldots \ldots \ldots\)
या \(\omega t=(2 n+1) \frac{\pi}{2}\) 
जहाँ n = 0, 1, 2, 3, 4, .........

(d) जब ऊर्जा प्रेरित्र तथा संधारित्र में समान रूप से वितरित होगी अर्थात वैद्युत् एवं चुम्बकीय ऊर्जा आधी - आधी होगी।
∴ पैद्युत ऊर्जा = \(\frac{1}{2} \times\) कुल ऊर्जा

(e) जब परिपथ में प्रतिरोध R प्रविष्ट कर दिया जाता है तो दोलन अवमंदित (damped) हो जाते हैं। प्रत्येक दोलन में कुछ ऊर्जा प्रतिरोध में ऊष्मा के रूप में क्षयित होती है, अत: कुछ समय पश्चात् सम्पूर्ण प्रारम्भिक ऊर्जा ऊष्या के रूप में क्षय (lost) हो जाती है।

प्रश्न 13. 
एक कुण्डली को जिसका प्रेरकत्व 0.50 H तथा प्रतिरोध 100Ω है, 240 V - 50 Hz की एक आपूर्ति (supply) से जोड़ा गया है।
(a) कुण्डली में अधिकतम धारा कितनी है? 
(b) वोल्टेज शीर्ष व धारा शीर्ष के बीच समय - पश्चता कितनी है?
हल: 
दिया है: L = 0.50 H; R = 100Ω; V_r = 240 V; f = 50 Hz; I_m = ? 
(a) कुण्डली का प्रेरणिक प्रतिघात 
X_L = 2πfL = 2 x 3.14 x 50 x 0.5
= 157Ω
∴ परिपथ की प्रतिबाधा

∴ परिपथ में अर्थात् कुण्डली में प्रवाहित अधिकतम धारा
\(\mathrm{I}_m=\frac{\mathrm{V}_m}{\mathrm{Z}}=\frac{339 \cdot 36}{186.14}=\mathbf{1 . 8 2} \mathbf{A}\)

(b) यदि वोल्टेज एवं धारा के मध्य कलान्तर के हो, तो
\(\begin{aligned} \tan \phi &=\frac{\mathrm{X}_{\mathrm{L}}}{\mathrm{R}}=\frac{157}{100}=1.57 \\ \therefore \quad \phi &=\tan ^{-1}(1.57)=57.5^{\circ} \end{aligned}\)
∴ समय - पश्चता (time - lag)
\(t=\frac{\mathrm{T}}{360} \times \phi=\frac{\mathrm{T}}{360} \times 57 \cdot 5^{\circ}\)
\(\therefore \quad t=\frac{1}{f} \times \frac{57.5}{360}\)
\(\begin{aligned} &=\frac{57.5}{50 \times 360} \\ &=0.00319 \\ &=3.19 \times 10^{-3} \mathrm{~s}=\mathbf{3 . 2} \mathrm{ms} \end{aligned}\)

प्रश्न 14. 
यदि परिपथ को उच्च आवृत्ति (high frequency) की आपूर्ति (240 V - 10 kHz) से जोड़ा जाता है, तो प्रश्न 13 (a) तथा (b) के उत्तर निकालिए। इससे इस कथन की व्याख्या (explain statement) कीजिए कि अति उच्च आवृत्ति (higher frequency) पर किसी परिपथ में प्रेरक लगभग खुले परिपथ के तुल्य होता है। स्थिर अवस्था (steady state) के पश्चात् किसी D.C. परिपथ में प्रेरक किस प्रकार का व्यवहार करता है?
हल: 
दिवा है: V_rms = 240 V; f = 10 kHz = 10 x 10³ Hz = 10⁴ Hz; L = 0.5 H; R = 100Ω
(a) X_L = 2πfL = 2 x 3.14 x 10⁴ x 0.5 = 31400Ω

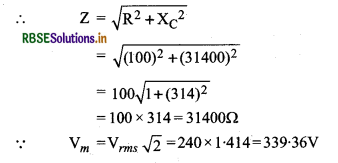
∴ I_m = \(\frac{\mathrm{V}_m}{\mathrm{Z}}=\frac{339.36}{31400}=0 \cdot 0108=\mathbf{0 . 0 1 1 \mathbf { A }}\)

(b) \(\tan \phi=\frac{\mathrm{X}_{\mathrm{L}}}{\mathrm{R}}=\frac{31400}{100}=314\)
\(\therefore \quad \phi=\tan ^{-1}(314)=89 \cdot 8 \approx 90^{\circ}\)
∴समय - पश्चता \(t=\frac{\phi}{\omega}=\frac{\phi}{2 \pi f}=\frac{90^{\circ}}{2 \times 180^{\circ} \times 10^4}\)
या \(t=\frac{1}{4} \times 10^{-4}\)
= 0.25 x 10^-4
= 2.5 x 10^-5 s
महत्तम धारा Im का मान अत्यन्त कम (0.011 A) है, इससे यह निष्कर्ष निकलता है कि अति उच्च आवृत्ति की धाराओं के लिए प्रेरक खुले परिपथ की भाँति व्यवहार करता है। 
∵दिष्ट धारा के लिए, f = 0
अतः X_L = 2πfL = 0
अत: दिष्ट धारा परिपथ में प्रेरक साधारण चालक की भाँति व्यवहार करता है।

प्रश्न 15. 
40Ω प्रतिरोध के श्रेणी क्रम में 100µF के संधारित्र को 110 V - 60 Hz की आपूर्ति से जोड़ा गया है।
(a) परिपथ में अधिकतम धारा कितनी है?
(b) थारा शीर्ष एवं वोल्टेज शीर्ष के बीच (between current maximum and voltage maximum) समय - पश्चता (time lag) कितनी है?
हल: 
दिया है: R = 40Ω; C = 100µF = 100 x 10^-6 F = 10^-4 F, Vr = 110 V; f = 60 Hz; I₀ = ?; t = ?
(a) धारितीय प्रतियात

(b) ∵ R - C परिपथ में विभवान्तर धारा से कला में पीछे होता है, 
अत: \(\tan \phi=-\frac{X_C}{R}=-\frac{26.54}{40}\) = -06635
\(\therefore \quad|\phi|=\tan ^{-1}(0.6635)=37.29=37.3^{\circ}\)
∴ समय - पश्चता
\(t=\frac{\phi}{\omega}=\frac{\phi}{\frac{2 \pi}{\mathrm{T}}}=\frac{\phi}{2 \pi} \times \mathrm{T}\)
या \(t=\frac{37 \cdot 3 \times \mathrm{T}}{2 \times 180^{\circ}}=\frac{37 \cdot 3}{360} \times \frac{1}{f}\)
या \(t=\frac{37.3}{360 \times 60}=0.0017268\)
\(\therefore \quad t=1.7268 \times 10^{-3} \mathrm{~s}=1.73 \mathrm{~ms}\)

प्रश्न 16. 
यदि परिपथ को 110 V - 12 kHz की आपूर्ति से जोड़ा जाये तो प्रश्न 15 (a) व (b) के उत्तर निकालिए। इससे इस कथन की व्याख्या कीजिए कि अति उच्च आवृत्तियों (at higher frequencies) पर एक संधारित्र चालक होता है। इसकी तुलना उस व्यवहार से कीजिए जो किसी D.C. परिपथ में एक संधारित्र प्रदर्शित करता है।
हल: 
दिया है: R = 40Ω,C = 100 µF = 100 x 10^-6 F = 10^-4 F; V_rms =110 V; f = 12 kHz = 12 x 10³ Hz; I_m = ?; t = ? 

∴ महत्तम धारा
\(I_m=\frac{V m}{Z}=\frac{V_{r m s} \cdot \sqrt{2}}{Z}\)
\(\therefore \quad \mathrm{I}_m=\frac{110 \times 1.414}{40}=\mathbf{3 . 8 8} \mathrm{A}\)

(b) \(\tan \phi=-\frac{X_C}{R}=-\frac{0.133}{40}=-0.00333\)
\(\therefore \quad|\phi|=\tan ^{-1}(0.00333)=0.21^{\circ}\)
∴ समय - पश्चता (time lag)
\(\begin{aligned} t &=\frac{\phi}{\omega}=\frac{\phi}{2 \pi f}=\frac{0.21^{\circ}}{2 \times 180 \times 12 \times 10^3} \\ \therefore \quad t &=0.000048 \times 10^{-3} \\ &=4.8 \times 10^{-8} \mathrm{~s} \end{aligned}\)
भाग (a) के उत्तर से यह निष्कर्ष निकलता है कि अति उच्च आवृत्ति के लिए संधारित्र का प्रतिघात (0.133Ω) नगण्य होता है अर्थात् संधारित्र एक शुद्ध चालक की भाँति व्यवहार करता है। स्थायी दिष्ट धारा (for steady d.c. current) हेतु
f = 0
अतः \(\mathrm{X}_{\mathrm{C}}=\frac{1}{2 \pi f \mathrm{C}}=\infty\)
इस प्रकार दिष्ट धारा के लिए संधारित्र खुले परिपथ की भाँति व्यवहार करता है।

प्रश्न 17. 
स्रोत की आवृत्ति एक श्रेणीबद्ध LCR परिपथ की अनुनादी आवृत्ति के बराबर रखते हुए तीन अवयवों L, C तथा R को समान्तर क्रम में लगाते हैं। यह दर्शाइए कि समान्तर LCR परिपथ में इस आवृत्ति पर कुल धारा न्यूनतम है। इस आवृत्ति के लिए प्रश्न 11 में निर्दिष्ट स्त्रोत तथा अवयवों के लिए परिपथ की हर शाखा में धारा के मान को परिकलित कीजिए।
हल: प्रश्न 11 से, L = 5.0H; C = 80 µF = 80 x 10^-6 F; R = 40Ω; V_rms = 230 V

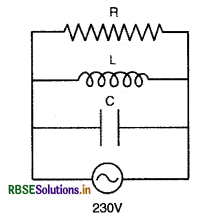
श्रेणी अनुनादी LCR परिपथ की कोणीय अनुनादी आवृत्ति
\(\begin{aligned} \omega_r=\frac{1}{\sqrt{\mathrm{LC}}} &=\frac{1}{\sqrt{5 \cdot 0 \times 80 \times 10^{-6}}} \\ &=\mathbf{5 0} \mathrm{rads}^{-1} \end{aligned}\)
L,C व R तीनों समान्तर क्रम में जुड़े हैं। परिपथ के ओमीय प्रतिरोध एवं परिपथ के प्रतिपात में π/2 का कलान्तर है। इसके साथ ही प्रेरणिक एवं धारितीय प्रतिघातों में π का कलान्तर है, अत: प्रतिघात का प्रभावी मान x दिया जाता है।
∴ समान्तर संयोजन (for parallel combination) के लिए
\(\frac{1}{\mathrm{X}}=\frac{1}{\mathrm{X}_{\mathrm{C}}}-\frac{1}{\mathrm{X}_{\mathrm{L}}}\)
क्योंकि X_L व X_C के मध्य का कलान्तर है। 
या \(\frac{1}{X}=\omega \mathrm{C}-\frac{1}{\omega \mathrm{L}}\)
यदि \(\hat{j}=\sqrt{-1}\) तो कॉम्प्लेक्स संख्या नोटेशन से 
\(\frac{1}{Z}=\frac{1}{\mathrm{R}}+\frac{1}{j \omega \mathrm{L}}+j \omega \mathrm{C}\)
या \(\frac{1}{\mathrm{Z}}=\frac{1}{\mathrm{R}}+j\left(\omega \mathrm{C}+\frac{1}{j^2 \omega \mathrm{L}}\right)\)
\(=\frac{1}{\mathrm{R}}+j\left(\omega \mathrm{C}-\frac{1}{\omega \mathrm{L}}\right)\), क्योंकि\( j^2=-1\)
अत: परिपथ की प्रतिबाधा, Z के लिए

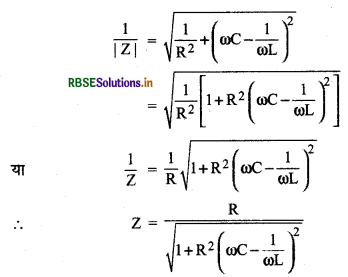
∵अनुनादी आवृत्ति पर,
\(\omega_r=\frac{1}{\sqrt{L C}} \quad \therefore \omega C-\frac{1}{\omega L}=0\)
\(\therefore \quad Z=\frac{\mathrm{R}}{\sqrt{1+0}}=\mathrm{R}\)
अनुनादी आवृत्ति पर प्रतिबाधा अधिकतम होगी जिसका मान
Z_max = R 
फलस्वरूप अनुनादी आवृत्ति पर धारा न्यूनतम होगी।
∴ कुल धारा \(I=\frac{V_{r m s}}{Z}=\frac{V_{r m s}}{R}=\frac{230}{40}=5.75 \mathrm{~A}\)

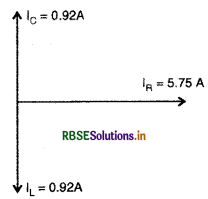
प्रतिरोध में धारा
\(\mathrm{I}_{\mathrm{R}}=\frac{\mathrm{V}_{r m s}}{\mathrm{R}}=\frac{230}{40}=5.75 \mathrm{~A}\)
संधारित्र में धारा
\(\begin{aligned} \mathrm{I}_{\mathrm{C}} &=\frac{\mathrm{V}_{r m s}}{\mathrm{X}_{\mathrm{C}}} \\ &=\mathrm{V}_{r m s} \times \omega \mathrm{C} \\ &=230 \times 50 \times 80 \times 10^{-6} \\ &=\mathbf{0 . 9 2} \mathbf{A} \end{aligned}\)
प्रेरकत्व में धारा
\(\mathrm{I}_{\mathrm{L}}=\frac{\mathrm{V}_{r m s}}{\mathrm{X}_{\mathrm{L}}}=\frac{\mathrm{V}_{r m s}}{\omega \mathrm{L}}=\frac{230}{50 \times 5}=0.92 \mathbf{A}\)
स्पष्ट है कि I = I_R + (I_L - I_C) क्योंकि I_L व I_C विपरीत कला में है।

प्रश्न 18. 
एक परिपथ में 80 mH का एक प्रेरक तथा 60µF का एक संधारित्र श्रेणीबद्ध है। इस परिपथ को 230V - 50 Hz की सप्लाई से जोड़ा जाता है। परिपथ का प्रतिरोध नगण्य है।
(a) धारा आयाम तथा धारा का rms मान ज्ञात कीजिए। 
(b) प्रत्येक अवयव के सिरों पर rms वोल्टेज ज्ञात कीजिए।
(c) प्रेरक को स्थानान्तरित माध्य शक्ति (average power transferred) कितनी है?
(d) संधारित्र को स्थानान्तरित यशक्ति कितनी है?
(e) परिपथ द्वारा अवशोषित माध्य शक्ति (total average power absorbed) कितनी है?
(माध्य शक्ति का अभिप्राय पूरे चक्र से है।)
हल: 
दिया है: L = 80 mH = 80 x 10^-3 H; C = 60 µF = 60x 10^-6 F;V = 230 V; f = 50Hz 
(a) प्रेरणिक प्रतिघात
\(\begin{aligned} \mathrm{X}_{\mathrm{L}} &=2 \pi f \mathrm{~L} \\ &=2 \times 3 \cdot 14 \times 50 \times 80 \times 10^{-3} \\ &=25 \cdot 13 \Omega \end{aligned}\)
धारितीय प्रतिघात
\(\begin{aligned} \mathrm{X}_{\mathrm{C}} &=\frac{1}{2 \pi f \mathrm{C}} \\ &=\frac{1}{2 \times 3 \cdot 14 \times 50 \times 60 \times 10^{-6}} \\ &=\frac{1000}{3 \cdot 14 \times 6}=53 \cdot 1 \Omega \end{aligned}\)
∴ प्रतिबाधा, अर्थात् नेट प्रतिघात
X = X_C - X_L
= 53.1 - 25.1 = 28.0 Ω
अतः धारा का आयाम
\(\mathrm{I}_m=\frac{\mathrm{V}_m}{\mathrm{Z}}=\frac{\mathrm{V}_{r m s} \cdot \sqrt{2}}{\mathrm{Z}}\)
\(\therefore \quad \mathrm{I}_m=\frac{230 \times 1 \cdot 414}{28 \cdot 0}=\mathbf{1 1 \cdot 6} \mathbf{A}\)
धारा का वर्ग माध्य मूल मान
\(I_{r m s}=\frac{I_m}{\sqrt{2}}=\frac{11 \cdot 6}{1.414}=8.24 \mathbf{A}\)

(b) प्रेरक के सिरों के मध्य ms वोल्टेज
V_L = X_L.I_rms = 25.13 x 8.24 = 207 V
संधारित्र की प्लेटों के मध्य ms वोल्टेज
V_C = X_C. I_rms = 53.1 x 8.2 = 437 V
नेट वोल्टेज V = V_C -V_L = 437 - 207
= 230 V 

(c) प्रेरकत्व के सिरों के मध्य विभवन्तर धारा से कला में π/2 आगे होता है
अर्थात् = \(\phi=\pi / 2 \therefore \cos \phi=0\)
∴ औसत शक्ति P = \(\mathrm{V}_{r m s} \mathrm{I}_{r m s} \cos \phi=\) 0 (शून्य)

(d) संधारित्र की प्लेटों के मध्य उत्पन्न भवान्तर धारा से π/2 पीछे होता है
अतः\(\phi=\pi / 2\)
∴ औसत शक्ति है P = 0 (शून्य)

(e) परिपथ द्वारा अवशोषित माध्य शक्ति (absorbed mean power) भी शून्य होगी।

प्रश्न 19. 
कल्पना कीजिए कि प्रश्न 18 में प्रतिरोध 15Ω है। परिपथ के हर अवयव को स्थानान्तरित माध्य शक्ति (average power transferred) तथा सम्पूर्ण अवशोषित शक्ति का परिकलन कीजिए।
हल: 
प्रश्न 18 से, L = 80 mH = 80 x 10^-3 H; C = 60µF = 60 x 10^-6 F; Vrms = 230 V; f = 50 Hz 
दिया है: R = 15Ω
प्रेरणिक प्रतिघात X_L = 25.1Ω(प्रश्न 18 से) 
धारितीय प्रतिघात X_C = 53.1Ω(प्रश्न 18 से) 
∴परिपथ का नेट प्रतियात
X = X_C - X_L = 53.1 - 25.1 = 28.0 Ω
परिपथ की प्रतिबाधा
\(\begin{aligned} Z &=\sqrt{\mathrm{R}^2+\mathrm{X}^2}=\sqrt{(15)^2+(28 \cdot 0)^2} \\ &=\sqrt{225+784}=\sqrt{1009} \\ &=31.76 \Omega=31.8 \Omega \end{aligned}\)
अतः धारा का ms मान
\(I_{r m s}=\frac{V_{r m s}}{Z}=\frac{230}{31.8}=7.23 \mathrm{~A}\)
धारा का आयाम अर्थात् शिखर मान
\(\begin{aligned} I_m &=I_{r m s} \cdot \sqrt{2} \\ &=7.23 \times 1.414=\mathbf{1 0 . 2 2} \mathbf{A} \end{aligned}\)
प्रतिरोध को स्थानान्तरित शक्ति
\(\begin{aligned} \mathrm{P}_{\mathrm{R}} &=\mathrm{I}_{r m s}^2 \cdot \mathrm{R} \\ &=(7 \cdot 23)^2 \times 15 \\ &=\mathbf{7 8 4 \cdot 0 9} \mathbf{W} \end{aligned}\)
प्रेरक व संधारित्र दोनों के लिए,
\(\phi=\pi / 2 \therefore \cos \phi=0 \)
अत: P_L = P_C = 0 
परिपथ द्वारा अवशोषित कुल शक्ति
P_T = P_R = 784.09 W

प्रश्न 20. 
एक श्रेणीबद्ध LCR परिपथ को, जिसमें L = 0.12 H, C = 480 nF; R = 23Ω, 230V की परिवर्ती आवृत्ति वाले स्रोत (variable frequency supply) से जोड़ा जाता है।
(a) स्त्रोत की किस आवृत्ति के लिए धारा आयाम अधिकतम है? इस अधिकतम मान को प्राप्त कीजिए।
(b) स्रोत की किस आवृत्ति के लिए परिपथ द्वारा अवशोषित माध्य शक्ति (average power absorbed) अधिकतम है?
(c) स्रोत की किस आवृत्ति के लिए परिपथ को स्थानान्तरित शक्ति आवृत्ति की शक्ति की आधी है?
(d) दिये गये परिपथ के लिए गुणता-कारक कितना है?
हल: 
दिया है: L = 0.12 H; C = 480 nF = 480 x 10^-9 F; R = 23Ω; V = 230 V
(a) धारा आयाम
\(\mathrm{I}_m=\frac{\mathrm{V}_m}{\mathrm{Z}}=\frac{\mathrm{V}_m}{\sqrt{\mathrm{R}^2+\left(\mathrm{X}_{\mathrm{C}}-\mathrm{X}_{\mathrm{L}}\right)^2}}\)
धारा आयाम अधिकतम तब होगा जब
\(\mathrm{X}_{\mathrm{C}}=\mathrm{X}_{\mathrm{L}}\)
\(\begin{aligned} \therefore \quad \mathrm{I}_m=\frac{\mathrm{V}_m}{\mathrm{R}}=\frac{\mathrm{V}_{r m s} \cdot \sqrt{2}}{\mathrm{R}} &=\frac{230 \times 1 \cdot 414}{23} \\ &=\mathbf{1 4 \cdot 1 4} \mathrm{A} \end{aligned}\)
अधिकतम धारा आयाम के (for maximum current amplitude) लिए
X_L = X_C \(\Rightarrow \omega_r L=\frac{1}{\omega_r C}\)


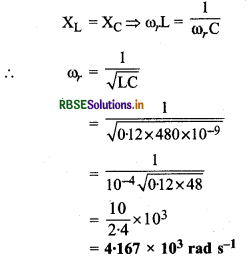
∴ अनुनादी आवृत्ति
\(\begin{aligned} f_0=\frac{\omega_r}{2 \pi} &=\frac{4.167 \times 10^3}{2 \times 3.14} \\ &=0.663 \times 10^3 \\ &=663 \mathrm{~Hz} \end{aligned}\)

(b) औसत शक्ति
P= V_rms I_rms. cos \(\phi\)
अधिकतम शक्ति के लिए
\(\cos \phi=+1\)
या \(\frac{\mathrm{R}}{\mathrm{Z}}=1 \Rightarrow \mathrm{Z}=\mathrm{R}\)
Z = R तभी होता है जब X = 0 अर्थात् X_L = X_C
स्पष्ट है कि अनुनादी आवृत्ति \(\omega_r\) पर ही औसत शक्ति अधिकतम होगी। 
∴ अधिकतम कोणीय आवृत्ति
\(\omega_0=\omega_r=4 \cdot 167 \times 10^3 \mathrm{rad} \mathrm{s}^{-1}\)
या \(f_0=663 \mathrm{~Hz}\)

(c) दिया है: अवशोषित शक्ति P =\( \frac{1}{2}\) x अधिकतम शक्ति

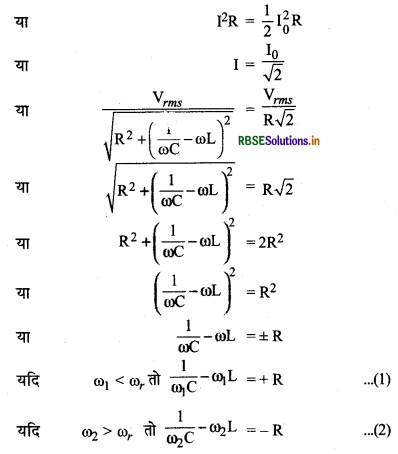
समी. (1) व (2) को जोड़ने पर,

समी. (2) को (1) में से पटाने पर,


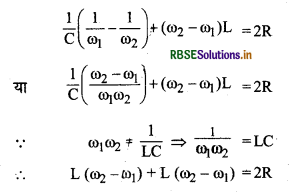
इस प्रकार अवशोषित शक्ति 647.8 Hz एवं 678.2 Hz आवृत्तियों पर अनुनादी आवृत्ति पर आरोपित शक्ति की आधी होगी। 

(d) दिये गये परिपथ का Q कारक
\(\begin{aligned} \mathrm{Q}=\frac{\omega_r \cdot L}{\mathrm{R}} &=\frac{4167 \times 10^3 \times 0.12}{23} \\ &=21.7 \end{aligned}\)

प्रश्न 21. 
एक श्रेणीबद्ध LCR परिपथ के लिए, जिसमें L = 30 H, C = 27 µF तथा R = 7.4 Ω, अनुनादी आवृत्ति तथा Q - कारक निकालिए। परिपथ के अनुनाद की तीक्ष्णता को सुधारने की इच्छा से (desired to improve thesharpness of resonance) अर्द्धबच्चिष्ठ पर पूर्ण चौड़ाई' (full width at half, maximum) को आधा कर दिया जाता है। इसके लिए उचित उपाय सुझाइए (suggest suitable way)।
हल: 
दिया है: L = 3.0 H; R = 7.4Ω; C = 27 µF = 27 x 10^-6 F

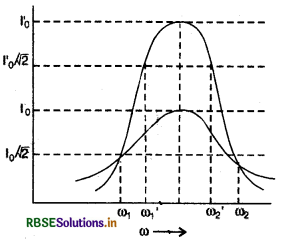
अनुनादी कोणीय आवृत्ति (resonand angular frequency)
\(\omega_r=\frac{1}{\sqrt{L C}}=\frac{1}{\sqrt{3 \cdot 0 \times 21 \times 10^{-6}}}\)
या \(\omega_r=\frac{1}{9 \times 10^{-3}}=\frac{1000}{9}=111 \mathrm{rad} \mathrm{s}\)
Q - कारक, Q = \(\begin{aligned} \frac{\omega_r}{\omega_2-\omega_1}=\frac{\omega_r \cdot \mathrm{L}}{\mathrm{R}} &=\frac{11 \times 3.0}{7 \cdot 4} \\ &=45 \end{aligned}\)
निश्चित\( \omega_r \)पूर्ण चौड़ाई \(\left(\omega_2-\omega_1\right)\) को घटाकर आधा कर दिया जाता है, जिससे Q - कारक दो गुना हो जाता है।
∵Q - कारक \(\propto \frac{1}{R}\), अत: Q - कारक प्रतिरोध को आधा करके दो गुना किया जा सकता है,
अर्थात् प्रतिरोध R = \(\frac{7.4}{2}=3.7 \Omega\)

प्रश्न 22. 
निम्नलिखित प्रश्नों के उत्तर दीजिए
(a) क्या किसी AC परिपथ में प्रयुक्त ताक्षणिक वोल्टता (applied instantaneous voltage) परिपथ में श्रेणी क्रम में जोड़े गये अवयवों के सिरों पर ताक्षणिक वोल्टताओं के बीजगणितीय योग के बराबर होती है? क्या यही बात rms वोल्टताओं में भी लागू होती है?
(b) प्रेरण कुण्डली के प्राथमिक परिपथ में एक संधारित्र का उपयोग करते हैं?
(c) एक प्रयुक्त वोल्टता संकेत एक DC  वोल्टता तथा उच्च आवृत्ति के एक AC वोल्टता के अध्यारोपण से निर्मित है। परिपथ एक श्रेणीबद्ध प्रेरक तथा संधारित्र से निर्मित है। दर्शाइए कि DC संकेत (signal) C तथा AC संकेत L के सिरे पर प्रकट होगा।
(d) एक लैम्प से श्रेणी क्रम में जुड़ी चोक को एक DC लाइन से जोड़ा गया है। लैम्प तेजी से चमकता (shine brightly) है। चोक में लोहे के कोड को प्रवेश कराने पर लैम्प की दीप्ति में कोई अन्तर नहीं पड़ता है। यदि एक AC लाइन से लैम्प का संयोजन किया जाये तो तद्नुसार प्रेक्षणों की प्रागुक्ति (prediet the corresponding observation) कीजिए।
(e) AC मेन्स के साथ कार्य करने वाली फ्लोरोसेन्ट ट्यूब (luoroscent tube) में प्रयुक्त चोक कुण्डली की आवश्यकता क्यों होती है? चोक कुण्डली के स्थान पर सामान्य प्रतिरोधक (normal resistor) का उपयोग क्यों नहीं होता?
उत्तर: 
(a) हाँ; परन्तु यह तथ्य rms वोल्टताओं के लिए सत्य नहीं है क्योंकि विभिन्न अवयवों की rms वोल्टताएँ समान कला में नहीं होती।

(b) संधारित्र को जोड़ने से, परिपथ को तोड़ते समय चिनगारी देने वाली धारा संधारित्र को आवेशित करती है, अत: चिनगारी नहीं निकल पाती।

(c) संधारित्र D - C सिग्नल को रोक देता है, अत: DC सिग्नल वोल्टता संधारित्र के सिरों पर प्रकट होगा, जबकि AC सिग्नल प्रेरक के सिरों पर प्रकट होगा।

(d) DC लाइन के लिए f = 0 
अत: चोक की प्रतिबाधा X_L = 2πfL = 0
अत: चौक DC के मार्ग में कोई रुकावट नहीं डालती, इसलिए लैम्प तेज चमकता है। AC लाइन जोड़ने पर चोक उच्च प्रतिघात (high reactance) उत्पन्न करती है। जब चौक में लोहे के क्रोड को प्रवेश कराते हैं तो उसका प्रेरकत्व बढ़ जाता है, अतः प्रतिघात X_L = 2πfL भी बढ़ जाता है। फलस्वरूप धारा \(\left(i=\frac{\mathrm{V}}{\mathrm{X}_{\mathrm{L}}}\right)\) कम हो जाती है और लैम्प की चमक कम हो जाती है।

(e) चोक कुण्डली एक प्रेरक का कार्य करती है और बिना शक्ति व्यय किये ही धारा को कम कर देती है। यदि चोक के स्थान पर प्रतिरोधक का प्रयोग करें तो वह धारा को कम कर देगा, परन्तु इसमें विद्युत् शक्ति ऊष्मा के रूप में व्यय होती रहेगी।

प्रश्न 23. 
एक शक्ति सम्प्रेषण लाइन (power transmission line) अपचायी (step down) ट्रान्सफॉर्मर में जिसकी प्राथमिक कुण्डली में 4000 फेरे हैं, 2300 वोल्ट पर शक्ति निवेशित (feeds) करती है। 230 V की निर्गत शक्ति प्राप्त करने के लिए द्वितीयक में कितने फेरे होने चाहिए?
हल: 
दिया है: N_P = 4000; V_P = 2300 V; V_S = 230 V; N_S = ?
\(\because \quad \frac{\mathrm{V}_s}{\mathrm{~V}_p}=\frac{\mathrm{N}_s}{\mathrm{~N}_p} \Rightarrow \mathrm{N}_s=\mathrm{N}_p \cdot \frac{\mathrm{V}_s}{\mathrm{~V}_p}\)
\(\therefore \quad \mathrm{N}_s=4000 \times \frac{230}{2300}=400\)

प्रश्न 24. 
एक जल - विद्युत् शक्ति संयन्त्र (hydroelectric power plant) में जल दाब शीर्ष 300 m की ऊंचाई पर है तथा उपलब्ध जल प्रवाह 100 ms^-1 है। यदि टरबाइन जनित्र की दक्षता 60% हो तो संयन्त्र से उपलब्ध विद्युत् शक्ति का आकलन कीजिए (g = 9.8 ms^-2)।
हल:
दिया है: h = 300 m; g = 9.8 ms^-2; जल का आयतन V= 100 m³; समय t = 1 s, जनित्र की दक्षता = 60% 
जल - विद्युत् शक्ति = जल स्तम्भ का दाब x प्रति सेकण्ड प्रवाहित जल का आयतन 
= hρg x V
= 300 x 10³ x 9.8 x 100
= 29.4 x 10⁷ W

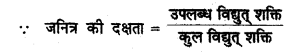
∴ उपलब्ध विद्युत् शक्ति = कुल विद्युत शक्ति x जनित्र की दक्षता
= 29.4 x 10⁷ x \(\frac{60}{100}\)
= 176.4 x 10⁶ W
= 176.4 MW 

प्रश्न 25.
440 V पर शक्ति उत्पादन करने वाले किसी विद्युत् संयन्त्र से 15 km दूर स्थित एक छोटे से कस्बे में 220 V पर 800 kW शक्ति की आवश्यकता है। विद्युत् शक्ति ले जाने वाली दोनों तार की लाइनों का प्रतिरोध 0.5Ω प्रति km है। कस्बे को उप - स्टेशन 4000 - 220 V अपचायी ट्रान्सफॉर्मर (step down transformer) से लाइन द्वारा शक्ति पहुंचती है।
(a) ऊष्मा के रूप में लाइन से होने वाली शक्ति के क्षय का आकलन कीजिए।
(b) संयन्त्र से कितनी शक्ति की आपूर्ति की जानी चाहिए, यदि क्षरण द्वारा शक्ति का क्षय नगण्य है।
(c) संयन्त्र के उच्चायी ट्रान्सफॉर्मर की विशेषता (characteristics) बताइए।
हल:
(a) तार की लाइनों का प्रतिरोध R = 30 km x 0.5 Ωkm^-1 = 15Ω उप - स्टेशन पर लगे ट्रान्सफॉर्मर से आपूर्ति की जाने वाली शक्ति, 

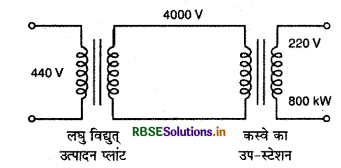
P = 800 kW = 800 x 10³ W 
वोल्टेज जिस पर शक्ति संचारित करनी है 
V = 4000 वोल्ट
∵ P= V.I ∴ I = \(\frac{\mathrm{P}}{\mathrm{V}}\)
या \(I_p=\frac{\mathrm{P}_p}{\mathrm{~V}_p}=\frac{800 \times 10^3}{4000}=200 \mathbf{A}\)
अत: लाइन शक्ति यस 
\(\mathrm{I}_p^2 \mathrm{R}=(200)^2 \times 15=6 \times 10^5 \mathrm{~W}=600 \mathrm{~kW}\)

(b) कुल आपूर्ति की जाने वाली शक्ति
= 800 kW + 600 kW = 1400 kW 
(c) लाइन में विभव पतन = Ip.R = 200 x 15 = 3000 V
संयन्त्र 440 V पर शक्ति का उत्पादन करता है तथा इसे इतना ऊँचा करना है कि 3000 V लाइन विभवपतन के बाद भी शहर तक 4000 V पर शक्ति पहुँच जाये, अत: निर्गत वोल्टेज (output voltage) = 3000+ 4000 = 7000 V
अत: यह ट्रान्सफॉर्मर 440 V - 7000 V प्रकार का होना चाहिए। 
∴ सप्लाई लाइन में प्रतिशत शक्ति क्षय (power loss)
\(=\frac{600 \mathrm{~kW}}{1400 \mathrm{~kW}} \times 100=42 \cdot 86 \%\)

प्रश्न 26. 
ऊपर दिये गए अभ्यास को पुनः कीजिए। इसमें पहले के ट्रांसफार्मर के स्थान पर 40,000 - 220 V अपचयी ट्रांसफॉर्मर है। पूर्व की भाँति क्षरण के कारण ह्यानियों को नगण्य मानिए, यद्यपि अब यह सन्निकटन उचित नहीं है क्योंकि इसमें उच्च वोल्टता पर संप्रेषण होता है।। अतः समझाइए कि क्यो उच्च वोल्टता संप्रेषण अधिक वरीय हैं? 
हल: 
अपचायी ट्रांसफार्मर की रेटिंग 40,000 V - 220 V
निवेशी वोल्टता V₁ = 40,000 V
निर्गत वोल्टता V₂ = 220 V
कुछ आवश्यक विद्युत शक्ति
P = 800 kw = 800 x 10³ w 
स्रोत विभव V = 220 V 
विद्युत संयंत्र द्वारा अपादित शक्ति की वोल्टता,
V = 440V 
शहर और शक्ति उत्पादन केन्द्र के बीच दूरी d = 15 km 
शक्ति संप्रेषण करने वाले तारों का प्रतिरोध = 0.5Ω/kw 
प्रतिरोधक तारों का कुल प्रतिरोध R = (15 + 15)0.5 = 15Ω
P = V₁I
तार में प्रवाहित धारा वर्ग माध्य मूल मान
\(I=\frac{P}{V_1}=\frac{800 \times 10^3}{40000}=20 \mathrm{~A} \)
(a) लाइन पॉवर क्षय = I²R
60² x 15 = 6 x 10³ w
= 6 kw 

(b) यह मानते हुए कि धारा लीकेज के कारण क्षय नगण्य प्लेट से संप्रेषित शक्ति 
= 800 kw + 6 kw = 806 kw 

(c) शक्ति में ड्रॉप = IR = 20 x 15 = 300 V 
अत: शक्ति केन्द्र द्वारा संप्रेषित वोल्टेज
300 + 40,000 = 40,300 V
केन्द्र में उत्पादित शक्ति 440 V की होगी। 
इस प्रकार केन्द्र पर उच्चायी ट्राँसफॉर्मर की रेटिंग 440 V - 40300 V 
इस प्रकार संप्रेषण के समय शक्ति क्षय
\(=\frac{600 \times 100}{1400} 42.8 \%\) 
इससे पूर्व के प्रश्न में, समान कारणों से शक्ति क्षय
\(=\frac{6}{806} \times 100=0.744 \%\) था 
अर्थात् उच्च वोल्टता संप्रेषण में शक्ति क्षय कम होत है। इसलिए अधिक दूरियों तक संप्रेषण में उच्च वोल्टता को प्राथमिकता दी जाती है।