RBSE Solutions for Class 12 Physics Chapter 6 वैद्युत चुंबकीय प्रेरण

Rajasthan Board RBSE Solutions for Class 12 Physics Chapter 6 वैद्युत चुंबकीय प्रेरण Textbook Exercise Questions and Answers.

RBSE Class 12 Physics Solutions Chapter 6 वैद्युत चुंबकीय प्रेरण

RBSE Class 12 Physics वैद्युत चुंबकीय प्रेरण Textbook Questions and Answers

प्रश्न 1.
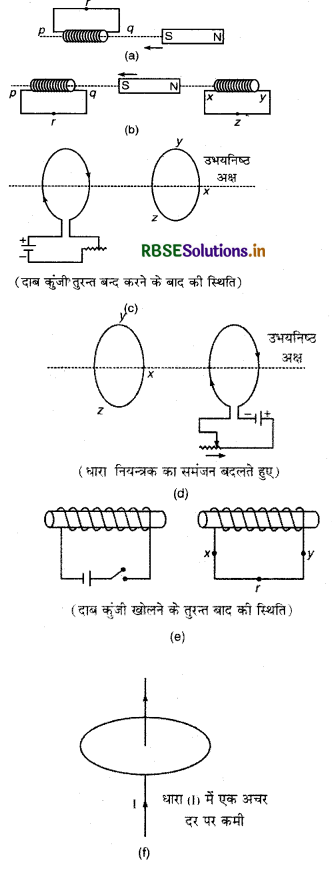
चित्र (a) से (f) में वर्णित स्थितियों के लिए (Forsituations described) प्रेरित धारा की दिशा की प्रागुक्ति (prediet) कीजिए।

उत्तर:
(a) चुम्बक का दक्षिणी ध्रुव कुण्डली के पास आ रहा है, अत: लेन्ज के नियमानुसार कुण्डली का q सिरा (end) दक्षिणी ध्रुव ही बनना चाहिए जिसके लिए प्रेरित धारा की दिशा qrpq दिशा में होगी।

(b) कुण्डली pq का q सिरा दक्षिणी ध्रुव (south pole) बनना चाहिए तभी चुम्बक के दक्षिणी धूव के पास आने का विरोध हो सकेगा। इसके लिए प्रेरित धारा prqp दिशा में बहेगी। इसी प्रकार कुण्डली xy का x सिरा दक्षिणी ध्रुव बनना चाहिए तभी चुम्बक के उत्तरी ध्रुव के दूर जाने का विरोध हो सकेगा, अत: प्रेरित धारा xyzx मार्ग का अनुसरण (follow) करेगी।

(c) प्रथम कुण्डली से जुड़ी कुंजी दबाते ही इसमें धारा शून्य से महत्तम मान की ओर बढ़ेगी। इस बढ़ती हुई धारा के कारण समीपस्थ कुण्डली में विपरीत दिशा में धारा प्रेरित होगी, अत: प्रेरित धारा xyzx मार्ग का अनुसरण (flow along path) करेगी।

(d) इंगित दिशा में धारा नियन्त्रक का समंजन बदलने पर परिपथ का प्रतिरोध घटेगा जिससे मूल धारा बढ़ेगी, अतः समीपस्थ कुण्डली में विपरीत दिशा में धारा प्रेरित होगी। इसलिए प्रेरित धारा zyxz मार्ग का अनुसरण करेगी।

(e) प्राथमिक कुण्डली में कुंजी खोलने के तुरन्त बाद द्वितीयक में समान धारा (अर्थात् कुंजी खोलने के पहले प्राथमिक में धारा) प्रेरित होगी, अतः द्वितीयक में प्रेरित धारा xryx मार्ग का अनुसरण करेगी।

(f) तार में प्रवाहित धारा के कारण चुम्बकीय क्षेत्र रेखाएँ लूप के तल के समान्तर है, अत: धारा परिवर्तन के कारण लूप से सम्बद्ध चुम्बकीय पलक्स में परिवर्तन नहीं होगा। फलस्वरूप लूप में कोई धारा प्रेरित नहीं होगी।

प्रश्न 2.
चित्र में प्रदर्शित परिस्थितियों में (situations described) लेन्ज के नियम का उपयोग करते हुए प्रेरित विद्युत् धारा की दिशा बताइए-
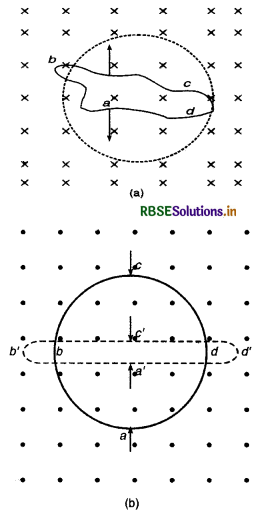
(a) जब अनियमित आकृति का तार वृत्ताकार बन रहा हो। 
(b) जब वृत्ताकार लूप एक सीधा तार बन रहा हो।

उत्तर:
(a) दी गई परिमाप के लिए वृत्त का क्षेत्रफल अधिकतम होता है। जब कुण्डली वृत्ताकार आकार लेती है तो उसका क्षेत्रफल बढ़ने से उससे सम्बद्ध चुम्बकीय फ्लक्स बढ़ता है। लेन्ज के नियम से कुण्डली में प्रेरित - धारा चुम्बकीय पलक्स के बढ़ने का विरोध करेगी। चित्र (a) में चुम्बकीय क्षेत्र कागज के तल के लम्बवत् नीचे की ओर है, अत: प्रेरित धारा ऊपर की ओर चुम्बकीय क्षेत्र उत्पन्न करेगी अर्थात् ऊपर वाला फलक उत्तरी ध्रुव बनना चाहिए। फलस्वरूप तार में प्रेरित धारा वामावर्त (Anticlockwise) दिशा में होनी चाहिए। इस प्रकार प्रेरित धारा adcba मार्ग का अनुसरण करेगी।

(b) दी गई परिमाप के लिए वृत्त का क्षेत्रफल अधिकतम होता है, अतः जब वृत्ताकार कुण्डली सीधे तार का आकार लेती है, तो कुण्डली से बद्ध चुम्बकीय क्षेत्र घटता है और लेन्ज के नियम से प्रेरित धारा चुम्बकीय फ्लास के घटने का विरोध करेगी। चूँकि आरोपित चुम्बकीय क्षेत्र ऊपर की ओर है, अत: प्रेरित धारा भी ऊपर की ओर चुम्बकीय क्षेत्र उत्पन्न करने का प्रयास करेगी फलस्वरूप कुण्डली में धारा वामावर्त दिशा a'd'c'b'a' का अनुसरण करेगी।

प्रश्न 3. 
एक लम्बी परिनालिका (long solenoid) की प्रति सेमी लम्बाई में 15 फेरे हैं। उसके अन्दर 2.0 cm² का एक छोटा - सा लूप परिनालिका की अक्ष के लम्बवत् रखा गया है। यदि परिनालिका में बहने वाली धारा का मान 0.1 s में 2.0 A से 4.0 A कर दिया जाये तो धारा परिवर्तन के दौरान प्रेरित वि. वा. बल क्या होगा? 
हल: 
परिनालिका कुण्डली का अन्योन्य प्रेरकत्व
M = µ₀n₁N₂A₂
= µ₀\(\left(\frac{\mathrm{N}_1}{l}\right)\)N₂A₂
यहाँ \(\left(\frac{\mathrm{N}_1}{l}\right)\) = 15 cm^-1 = 15 x 100 m^-1 = 1500 m^-1; N₂ = 1; A₂ = 2.0 cm² = 2.0 x 10^-4 m²;
∴ M = 4π x 10^-7 x 1500 x 1 x 2 x 10^-4
= 120π x 10^-9 H
अत: लूप में प्रेरित वि. वा. बल
e = \(\mathrm{M} \frac{\Delta \mathrm{I}_1}{\Delta t}\) (आंकिक मान)
= 120 \(\pi \times \frac{10^{-9} \times(4-2)}{0.1}\)
= 120 x 3.14 x 10^-8 x 2
= 7.5 x 10^-6 V = 7.5 µV

प्रश्न 4.
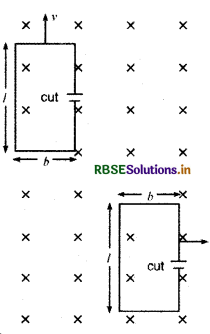
एक आयताकार लूप (rectangular loop) जिसकी भुजाएं 8 cm एवं 2 cm हैं, एक स्थान पर थोड़ा कटा हुआ है। यह लूप अपने तल के अभिलम्बवत् 0.3 T के एकसमान चुम्बकीय क्षेत्र से बाहर निकल रहा है। यदि लूप के बाहर निकलने का वेग 1 cm s^-1 है, तो निम्न परिस्थितियों में कटे भाग के सिरों पर उत्पन्न विभवान्तर ज्ञात कीजिए-
(i) जब लूप की गति लम्बी भुजा के लम्बवत् हो, 
(ii) जब लूप की गति छोटी भुजा के लम्बवत् हो। 
प्रत्येक स्थिति में उत्पन्न विभवान्तर कितने समय तक रहेगा?

हल: 
दिया है: l = 8 cm = 8 x 10^-2 m; b = 2 cm = 2 x 10^-2 m; B = 0.3 T; v = 1cm s^-1 = 1 x 10^-2 ms^-1
(i) जब वेग लम्बी भुजा के लम्बवत् है, तो प्रेरित वि. वा. बल
e = Bvl = 0.3 x 1 10^-2 x 8 x 10^-2
=2.4 x 10^-4 V
लप में प्रेरित वि. वा. बल तभी तक रहेगा जब तक लूप चुम्बकीय क्षेत्र के अन्दर रहेगा।
∴ प्रेरित वि. वा. बल की अवधि
t = \(\frac{b}{v}=\frac{2 \times 10^{-2}}{1 \times 10^{-2}}\) = 2s

(ii) जब वेग छोटी भुजा के लम्बवत् है तो प्रेरित वि. वा. बल
e = Bvb = 0.3 x 1 x 10^-2 x 2 x 10^-2
= 0.6 x 10^-4 V
इस वि. वा. बल की अवधि
t = \(\frac{l}{v}=\frac{8 \times 10^{-2}}{1 \times 10^{-2}}\) = 8s

प्रश्न 5.
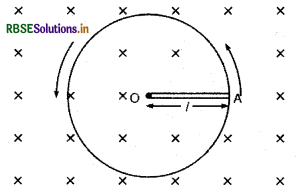
1m लम्बी धातु की छड़ उसके एक सिरे से गुजरने वाली अभिलम्बवत् अक्ष के परितः 400 rad s^-1 की कोणीय आवृत्ति (angular frequency) से घूम रही है। छड़ का दूसरा सिरा एक यात्विक वलय (metallic ring) से सम्पकित है। अक्ष के अनुदिश सभी जगह 0.5 T का एक समान चुम्बकीय क्षेत्र उपस्थित है। वलय तथा अक्ष के बीच स्थापित वि, वा, बल की गणना कीजिए।

हल: 
वलय तथा अक्ष के मध्य उत्पन्न प्रेरित वि. वा. बल (The emf developed between the centre and the ring)
e = \(\frac{1}{2} \mathrm{~B} \omega l^2\)
यहाँ B = 0.5 T, ω = 400 rad s^-1; l =1m 
∴ e = \(\frac{1}{2}\) x 0.5 x 400 x 1 x 1
= 100 V

प्रश्न 6. 
एक वृत्ताकार कुण्डली जिसकी त्रिज्या 8.0 cm तथा फेरों की संख्या 20 है, अपने ऊर्ध्व व्यास (Vertical diameter) के परित: 50 rad s^-1 की कोणीय आवृत्ति से 3.0 x 10^-2 T के एकसमान चुम्बकीय क्षेत्र में घूम रही है। कुण्डली में उत्पन्न अधिकतम तथा औसत प्रेरित वि. वा. बल का मान ज्ञात कीजिए। यदि कुण्डली 10Ω प्रतिरोध का एक बन्द लूप बनाए तो कुण्डली में धारा के अधिकतम मान की गणना कीजिए। जूल ऊष्मन (joule heating) के कारण क्षयित औसत शक्ति की गणना कीजिए। यह शक्ति कहाँ से प्राप्त होती है?
हल : कुण्डली से बढ़ चुम्बकीय फ्लक्स 
φB = \(\overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{A}}\) = BA Cosθ = BA Cosωt, क्योंकि θ = ωt
∴ कुण्डली में प्रेरित वि. वा. बल
e = \(-\mathrm{N} \frac{d \phi_{\mathrm{B}}}{d t}=-\mathrm{N} \cdot \frac{d}{d t}(\mathrm{BA} \cos \omega t)\)
⇒ e = -N.BA(-sinωt).ω
⇒ e = NBAω sinωt
जब ω = \(\pi / 2\)  तो  \(\sin \omega t=1\)
∴ emax = NBAω
यहाँ N = 20; r = 8.0 cm = 8.0 x 10^-2 m; B = 3.0 x 10^-2 T; ω = 50 rad s^-1
A = πr² = 3.14 (8.0 x 10^-2)²
∴ e_max = 20 x 3.0 x 10^-2 x 3.14 x (8.0 x 10^-2)² x 50
= 0.603 V 
औसत प्रेरित वि. वा. बल
e_av = BAN.ω (sinωt)av = 0 (शून्य) 
क्योंकि पूरे चक्र के लिए sinωt का औसत मान शून्य होगा। 
अधिकतम प्रेरित धारा
\(\mathrm{I}_{\max }=\frac{e_{\max }}{\mathrm{R}}=\frac{0 \cdot 603}{10}\) = 0.0603 A
जूल उष्मन के कारण औसत व्यय शक्ति (Power dissipated due to Joule heating)
P_max = (I²)_av.R =\(\frac{\left(e^2\right)_{a v}}{\mathrm{R}}=\frac{1}{2} \frac{e_{\max ^2}}{\mathrm{R}}\) [क्योंकि पूरे चक्र के लिए sin2ωt का औसत मान \(\frac{1}{2}\) होता है ∴\(e_{a v}^2=\frac{e^2 \max }{2}\)]
∴ P_max = \(\frac{1}{2} \times \frac{(0 \cdot 603)^2}{10}\) = 0.018 V
कुण्डली में प्रेरित धारा एक बल आपूर्ण उत्पन्न करती है, जो कुण्डली के घूमने का विरोध करता है, इसलिए कुण्डली को एकसमान कोणीय वेग (uniform angular velocity) से घुमाये रखने के लिए एक बाहा कारक (रोटर) बल - आघूर्ण प्रदान करता है। इसीलिए व्यय ऊष्मा का स्रोत गेटर (rotor) ही है।

प्रश्न 7. 
पूर्व से पश्चिम दिशा में विस्तृत एक 10 m लम्बा क्षैतिज सीधा तार 0.30 x 10^-4 Wbm^-2 तीव्रता वाले पृथ्वी के चुम्बकीय क्षेत्र के क्षैतिज घटक से लम्बवत 5.0 ms^-1 की चाल से गिर रहा है।
(a) तार में प्रेरित विद्युत वाहक बल का तातक्षणिक मान क्या होगा?
(b) विद्युत वाहक बल की दिशा क्या है? 
(c) तार का कौनसा सिरा उच्च विद्युत विभव पर है? 
हल: 
(a) तात्कालिक वि. वा. बल
e = Bvl = H.vl
दिया है: H = 0.30 x 10^-4 T; l = 10 m; v = 5.0 ms^-1
∴ e = 0.30 x 10^-4 x 5.0 x 10
= 1.5 x 10^-3 V = 1.5 mV

(b) फ्लेमिंग के दायें हाथ के नियम से, तार में प्रेरित धारा की दिशा पश्चिम से पूर्व की ओर होगी, अतः प्रेरित वि. वा. बल की दिशा पश्चिम से पूर्व की ओर होगी।

(c)∴ लॉरंज बल

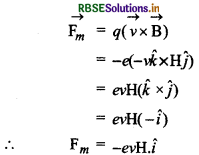
स्पष्ट है कि चालक के मुक्त इलेक्ट्रॉनों पर बल ऋणात्मक (-ve) X - दिशा में लगेगा, अत: वे चालक के पश्चिमी सिरे की ओर गति करेंगे। फलस्वरूप चालक का पूर्वी सिरा धनात्मक होगा।

प्रश्न 8. 
किसी परिपथ में धारा 0.1 s में 5.0 A से 0.0 A तक गिरती है। यदि परिपथ में औसत प्रेरित वि. वा. बल 200 V हो, तो परिपथ का स्वप्रेरकत्व ज्ञात कीजिए।
हल: 
स्वप्रेरित वि. वा. बल
\(e_{\mathrm{L}}=-\mathrm{L} \frac{\Delta \mathrm{I}}{\Delta t}\)
दिया है:
\(\begin{aligned} &\Delta t=0 \cdot 1 \mathrm{sec} \\ &\Delta \mathrm{I}=\mathrm{I}_2-\mathrm{I}_1=0-5 \cdot 0=-5 \cdot 0 \mathrm{~A} \\ &e_{\mathrm{L}}=200 \mathrm{~V} ; \mathrm{L}=? \end{aligned}\)
\(\therefore \quad 200=\frac{-\mathrm{L}(-5 \cdot 0)}{0 \cdot 1}=50 \mathrm{~L}\)
\(\therefore \quad \mathrm{L}=\frac{200}{50}=\mathbf{4} \mathbf{H}\)

प्रश्न 9. 
निकटवर्ती कुण्डलियों (adjacent cells) के एक युग्म (pair) का अन्योन्य प्रेरकत्व 1.5 H है। यदि एक कुण्डली में धारा 0.5 s में 0 A से 20 A तक परिवर्तित होती है तो दूसरी कुण्डली से बद्ध चुम्बकीय फ्लक्स (change of magnetie flux linkage) में कितना परिवर्तन होगा? 
हल: 
दूसरी कुण्डली से सम्बद्ध चुम्बकीय फ्लक्स
\(\phi_2=\mathrm{MI}_1\)
∴चुम्बकीय फ्लक्स में परिवर्तन
\(\Delta \phi_2=\mathrm{M} \Delta \mathrm{I}_1\)
दिया है: M = 1.5 H; ∆I =20 - 0 = 20 A
\(\therefore \quad \Delta \phi_2=1.5 \times 20\) = 30 वेबर 

प्रश्न 10.
एक जेट प्लेन पश्चिम की ओर 1800 kmh^-1 के वेग से गतिमान है। प्लेन के पंख (wings) 25 m लम्बे हैं। इनके सिरों के बीच कितना विभवान्तर प्रेरित होगा? उस स्थान पर चुम्बकीय क्षेत्र का मान 5 x 10^-4 टेस्ला तथा नमन कोण 30° है।
हल: 
गतिमान प्लेन के पंखों से पृथ्वी के चुम्बकीय क्षेत्र का ऊर्ध्व घटक (horizontal component) कटेगा जिससे उनके मध्य वि. वा. बल प्रेरित हो जायेगा जिसका मान
e = vBl = vVl
जहाँ V = पृथ्वी के चुम्बकीय क्षेत्र का ऊर्ध्व घटक
दिया है: पृथ्वी का चुम्बकीय क्षेत्र Be = 5 x 10^-4 T; 
नमन कोण θ = 30° 
पंखों की नोकों के मध्य दूरी l = 25 m;
v = 1800 x \(\frac{5}{18}\)
= 500 ms^-1 
∵ पृथ्वी के चुम्बकीय क्षेत्र का ऊर्व घटक
V = Be sinθ
= 5 x 10^-4 x sin 30° 
= 5 x 10^-4 x \(\frac{1}{2}\)
= 2.5 x 10^-4 T
∴ e =vVl = 500 x 2.5 x 10^-4 x 25
= 312.5 x 10^-2 = 3.1 V

प्रश्न 11. 
8 cm x 2 cm भुजाओं वाला एक आयताकार बन्द लूप (rectangular closed loop) विद्युत् चुम्बक द्वारा उत्पन्न एक समान चम्बकीय क्षेत्र में स्थिर है। विद्युत् चुम्बक में बहने वाली धारा को धीरे - धीरे घटाया जाता है, ताकि चुम्बकीय क्षेत्र अपने प्रारम्भिक मान 0.3 T से 0.02 Ts^-1 की दर से घटने लगता है। यदि लूप का प्रतिरोध 1.6 Ω है, तो लूप द्वारा ऊष्मा के रूप में व्यय शक्ति (power loss due to heat) कितनी होगी? इस शक्ति का स्रोत क्या है? 
हल: 
लूप का क्षेत्रफल
A = 8 x 2 = 16 cm^² = 16 x 10^-4 m
प्रेरित वि. वा. बल
e = \(-\frac{\Delta \phi}{\Delta t}=-\frac{\Delta(\mathrm{BA})}{\Delta t}=-\mathrm{A} \cdot \frac{\Delta \mathrm{B}}{\Delta t}\)
यहाँ \(\frac{\Delta \mathrm{B}}{\Delta t}=-0.02 \mathrm{Ts}^{-1}\)
∴ e = -16 x 10^-4 (-0.02)
= 3.2 x 10^-5 V
∴लूप में प्रवाहित प्रेरित धारा
\(\mathrm{I}=\frac{e}{\mathrm{R}}=\frac{3 \cdot 2 \times 10^{-5}}{1 \cdot 6}=2 \times 10^{-5} \mathrm{~A}\)
अतः शक्ति क्षय P= I²R = (2 x 10^-5)² x 1.6
= 6.4 x 10^-10 W
इस शक्ति का स्रोत विद्युत् चुम्बक को धारा प्रदान करने वाला बाहर लोत है।

प्रश्न 12. 
12 m भुजा वाला एक वर्गाकार लूप (square loop) जिसकी भुजाएँ X एवं Y अक्षों के अनुदिश हैं, X - दिशा में 8 cms^-1 की गति से धनात्मक Z - दिशा में दिष्ट चुम्बकीय क्षेत्र के परिवेश (environment) में चलाया जा रहा है। चुम्बकीय क्षेत्र न तो एकसमान है और न ही समय के साथ नियत है। इस क्षेत्र की ऋणात्मक X - दिशा में प्रवणता (gradient) 10^-3 T cm^-1 है (अर्थात् ऋणात्मक X - दिशा में प्रवणता 10^-3 T cm^-1 की वृद्धि होती है तथा यह समय के साथ 10^-3  Ts^-1 की दर से घट रहा है। यदि लूप का प्रतिरोध 4.50 mΩ हो तो इसमें प्रेरित धारा का परिमाण तथा दिशा ज्ञात कीजिए।
हल: 
वर्गाकार लूप की भुजा
l = 12 cm = 12 x 10^-2 m 
∴ लूप का क्षेत्रफल
A = l² = (12 x 10^-2)²
= 144 x 10^-4 m²
चुम्बकीय क्षेत्र की प्रवणता
\(\frac{d \mathrm{~B}}{d x}=-10^{-3} \mathrm{~T} \mathrm{~cm}^{-1}\)
= -10^-1 T m^-1
समय के साथ चुम्बकीय क्षेत्र की तीव्रता के परिवर्तन की दर
\(\frac{d \mathrm{~B}}{d t}=-10^{-3} \mathrm{Ts}^{-1}\)
लूप का प्रतिरोध R = 4.5 mΩ = 4.5 x 10^-3 Ω
असमान चुम्बकीय क्षेत्र में लूप की गति के कारण चुम्बकीय फ्लक्स में परिवर्तन की दर

चुम्बकीय क्षेत्र के समय के साथ परिवर्तन के कारण चुम्बकीय फ्लक्स में परिवर्तन की दर
\(\begin{aligned} \frac{d \phi_2}{d t} &=\frac{d}{d t} \cdot(\mathrm{BA})=\mathrm{A} \cdot \frac{d \mathrm{~B}}{d t} \\ &=144 \times 10^{-4} \times\left(-10^{-3}\right) \\ &=-1.44 \times 10^{-5} \mathrm{Wbs}^{-1} \end{aligned}\)
∴ चुम्बकीय फ्लक्स में परिवर्तन की दर
\(\begin{aligned} \frac{d \phi}{d t} &=\frac{d \phi_1}{d t}+\frac{d \phi_2}{d t} \\ &=-11.52 \times 10^{-5}-1.44 \times 10^{-5} \\ &=-12.96 \times 10^{-5} \mathrm{Wbs}^{-1} \end{aligned}\)
ऋणात्मक चिह फ्लक्स के घटने का प्रतीक है। प्रेरित वि. वा. बल
e = \(-\frac{d \phi}{d t}=12.96 \times 10^{-5} \mathrm{~V}\)
अतः प्रेरित धारा
\(\begin{aligned} \mathrm{I} &=\frac{e}{\mathrm{R}}=\frac{12 \cdot 96 \times 10^{-5}}{4 \cdot 5 \times 10^{-3}} \\ &=2.88 \times 10^{-2}=28 \cdot 8 \times 10^{-3} \mathrm{~A} \end{aligned}\)
∴ I = 28.8 mA
प्रेरित धारा की दिशा इस प्रकार होगी जो Z - दिशा में चुम्बक फ्लक्स के घटने का विरोध कर सके, अतः धारा वामावर्त दिशा में होगी।

प्रश्न 13. 
एक शक्तिशाली लाउडस्पीकर (powerful loudspeaker) के चुंबक धूवों के बीच चुम्बकीय क्षेत्र की तीव्रता के परिमाण को मापना है। इसके लिए 2 cm² क्षेत्रफल की एक छोटी चपटी (flat) अन्वेषी कुण्डली (Search coil) का प्रयोग किया जाता है। इस कुण्डली में पास - पास लिपटे 25 फेरे हैं तथा इसे चुम्बकीय क्षेत्र के लम्बवत् व्यवस्थित (positioned normal) किया गया है। अन्वेषी कुण्डली को अचानक चुम्बकीय क्षेत्र के बाहर निकाला (quickly smatched out) जाता है। तुल्यतः (equivalently) अन्वेषी कुण्डली को तेजी से 90° घुमा दिया जाता है, ताकि कुण्डली का तल चुम्बकीय क्षेत्र के समांतर हो जाये। इन दोनों घटनाओं में समान कुल आवेश 7.5 mC का प्रवाह होता है (जिसे प्रक्षेप धारामापी (Ballistic galvanometer) लगाकर ज्ञात किया जा सकता )। यदि कुण्डली तथा धारामापी का प्रतिरोध 0.50 Ω है तो चुम्बक के चुम्बकीय क्षेत्र की प्रबलता (field strength) ज्ञात कीजिए।
हल: 
कुण्डली में प्रेरित आवेश = \(\frac{\mathrm{N} \Delta \phi}{\mathrm{R}}\)
प्रक्षेप धारामापी आवेश को मापने के लिए विशेष रूप से बनाया गया धारामापी है।
दिया है: N = 25; A = 2 cm² = 2 x 10^-4 m²; q = 7.5 mC = 7.5 x 10^-3 C; R = 0.50 Ω
जब कुण्डली को चुम्बकीय क्षेत्र से बाहर खींचा जाता है, तो चुम्बकीय फ्लक्स में परिवर्तन
\(\Delta \phi=0-\text { BA }\)
= -BA = BA (आंकिक मान)
∴ प्रेरित आवेश q = \(\frac{\mathrm{NBA}}{\mathrm{R}}\)  
∴ चुम्बकीय क्षेत्र B = \(\frac{q \mathrm{R}}{\mathrm{NA}}\)
= \(\frac{7.5 \times 10^{-3} \times 0.50}{25 \times 2 \times 10^{-4}}=0.75 \mathrm{~T}\)

प्रश्न 14.
चित्र में एक धातु की छड़ (metal rod) PQ को दर्शाया गया है जो पटरियों AB पर रखी है तथा एक स्थायी चुम्बक के ध्रुवों के मध्य स्थित है। पटरियाँ, छड़ एवं चुम्बकीय क्षेत्र परस्पर अभिलम्बवत् दिशाओं में हैं। एक गैल्वेनोमीटर (धारामापी) G को पटरियों से एक स्विचर K की सहायता से संयोजित किया गया है। छड़ की लम्बाई = 15 cm, B = 0.50 T तथा पटरियों, छड़ तथा धारामापी से बने बन्द लूप का प्रतिरोध = 9.0 mΩ  है। क्षेत्र को एकसमान मान लें।

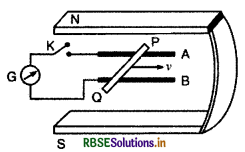
(a) माना कुंजी K खुली (open) है तथा छड़ 12 cms^-1 की चाल से दर्शायी गई दिशा में गतिमान है। प्रेरित वि. वा. बल का मान एवं घुवता (Polarity) बताइए।
(b) क्या कुंजी K खुली होने पर छड़ के सिरों पर आवेश का आधिक्य (excess charge) हो जायेगा? क्या होगा यदि कुंजी र बन्द (close) कर दी जाये।
(c) जब कुंजी K खुली हो तथा छड़ एकसमान वेग से गति में हो तब भी इलेक्ट्रॉनों पर कोई परिणामी बल कार्य नहीं करता यद्यपि उन पर छड़ की गति के कारण चुम्बकीय बल कार्य करता है। कारण स्पष्ट कीजिए।
(d) कुंजी बन्द होने की स्थिति में छड़ पर लगने वाले अवमन्दन बल (retarding force) का मान क्या होगा?
(e) कुंजी बन्द होने की स्थिति में छड़ को उसी चाल ( = 12 ms^-1) से चलाने हेतु कितनी शक्ति (बाह्य कारक के लिए) की आवश्यकता होगी?
(f) बन्द परिपथ में कितनी शक्ति का ऊष्मा के रूप में क्षय होगा? इस शक्ति का स्रोत क्या है? 
(g) गतिमान छड़ में उत्पन्न वि. वा. बल का मान क्या होगा यदि चुम्बकीय क्षेत्र की दिशा पटरियों (rails) के लम्बवत् होने की बजाय उनके समान्तर हो?
हल: 
दिया है: B = 0.50 T; l = 0.15 m; v = 0.12 ms^-1; R = 9.0 x 10^-³Ω
(a) छड़ में प्रेरित विद्युत् वाहक बल
e = vBl
= 0.12 x 0.50 x 0.15
= 9 x 10^-3 V = 9.0 mV

(b) हाँ, छड़ के सिरे पर इलेक्ट्रॉन एकत्र हो जायेंगे जबकि P सिरे पर धनावेश की अधिकता हो जायेगी।
यदि कुंजी K को बन्द कर दिया जाये तो सिरे पर एकत्र होने वाले इलेक्ट्रॉन बन्द परिपथ से होते हुए (G से होकर) सिरे P की ओर गति करने लगेंगे। इस प्रकार परिपथ में स्थायी धारा (stable current) स्थापित हो जायेगी।

(c) जब कुंजी K खुली हो तो P सिरा धनात्मक एवं सिरा ऋणात्मक हो जाता है। इससे छड़ के भीतर सिरे P से सिरे की ओर एक विद्युत् क्षेत्र स्थापित हो जाता है। इस क्षेत्र के कारण इलेक्ट्रॉनों पर Q से P की ओर विद्युत् बल लगता है जो विपरीत दिष्ट चुम्बकीय बल (opposite directive magnetic field) को सन्तुलित कर लेता है।
इस प्रकार इलेक्ट्रॉनों पर कोई नेट बल कार्य नहीं करता है। 

(d) कुंजी K बन्द होने की स्थिति में छड़ PQ से प्रवाहित धारा
\(i=\frac{e}{\mathrm{R}}=\frac{9 \times 10^{-3} \mathrm{~V}}{9 \cdot 0 \times 10^{-3} \Omega}=1.0 \mathrm{~A}\)
∴ छड़ PQ पर चुम्बकीय क्षेत्र के कारण कार्य करने वाला अवमन्दन बल
F = ilB sin 90°
= 1.0 x 0.15 x 0.50 
= 75 x 10^-3 N = 0.075 N

(e) कुंजी के बन्द होने पर छड़ को खींचते रहने के लिए व्यय की जाने वाली शक्ति
P = Fv
= 0.075 x 0.12
= 9 x 10^-3 W

(f) परिपथ में व्यय ऊष्मीय शक्ति
P = i²R
= (1.0)² x 9.0 x 10^-3
= 9 x 10^-3 W
इस शक्ति का स्रोत छड़ को एकसमान वेग से खींचते रहने के लिए बाहा स्रोत द्वारा व्यय की गई शक्ति है।

(g) शून्य; इस स्थिति में छड़ चुम्बकीय क्षेत्र रेखाओं को नहीं काटेगी, अत: कोई वि. वा. बल प्रेरित नहीं होगा।

प्रश्न 15. 
एक वायु क्रोड परिनालिका (air - cored solenoid) की लम्बाई 30 cm, अनुप्रस्थ काट का क्षेत्रफल 25 cm² तथा फेरों की संख्या 500 है। परिनालिका में 2.5 A की धारा बह रही है। धारा को अल्प काल (brief time)10^-3 s में अचानकबन्दकर (suddenly switched of दिया जाता है। परिपथ में स्विच के खुले सिरों के परितः उत्पन्न औसत वि. वा, बल कितना होगा? परिनालिका के सिरों पर चुम्बकीय क्षेत्र के परिवर्तन की उपेक्षा कीजिए। 
हल: 
परिनालिका में प्रेरित वि. वा. बल
e = \(-\mathrm{L} \frac{\Delta \mathrm{I}}{\Delta t}\)
परिनालिका का स्वप्रेरकत्व
\(\mathrm{L}=\frac{\mu_0 \mathrm{~N}^2 \mathrm{~A}}{l}\)
∴ e = \(\left(\frac{\mu_0 \mathrm{~N}^2 \mathrm{~A}}{l}\right) \frac{\Delta \mathrm{I}}{\Delta t}\)
यहाँ N= 500; A = 25 cm² = 25 x 10-4 m²; l = 30 cm = 0.30 m
\(\begin{aligned} \frac{\Delta \mathrm{I}}{\Delta t}=& \frac{\mathrm{I}_2-\mathrm{I}_1}{\Delta t}=\frac{0-2 \cdot 5}{10^{-3}} \\ &=-2.5 \times 10^3 \mathrm{~A} \mathrm{~s}^{-1} \end{aligned}\)
∴ प्रेरित वि. वा. बल
\(\begin{aligned} e &=-\left[\frac{4 \pi \times 10^{-7} \times(500)^2 \times 25 \times 10^{-4}}{0.30}\right] \times\left(-2.5 \times 10^3\right) \\ &=\frac{3.14 \times 25 \times 2.5}{3} \times 10^{-1} \\ &=6.5 \mathrm{~V} \end{aligned}\)

प्रश्न 16. 
(a) चित्र में प्रदर्शित एक लम्बे सीधे तार तथा a भुजा वाले एक वर्गाकार लूप के लिए अन्योन्य प्रेरकत्व का व्यंजक प्राप्त कीजिए।
(b) लूप में उत्पन्न प्रेरित वि. वा. बल का परिकलन कीजिए। यदि तार में 50 A की धारा बह रही हो तथा लूप का किसी क्षण x = 0.2 m पर तात्कालिक वेग (instantaneous velocity) 10 ms^-1 हो जैसा कि चित्र में प्रदर्शित है। a = 0.1 m लीजिए तथा यह मानिए कि लूप का प्रतिरोध बहुत अधिक है।

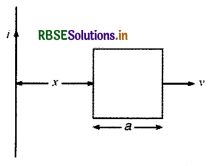
हल: 
(a) माना लूप, तार की लम्बाई के समान्तर अनेक छोटे-छोटे खण्डों से मिलकर बना है। माना तार से r दूरी पर एक छोटा खण्ड dr चौड़ाई का है। खण्ड की स्थिति पर धारावाही तार द्वारा उत्पन्न चुम्बकीय क्षेत्र

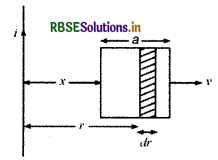
\(\mathrm{B}=\frac{\mu_0 \mathrm{I}}{2 \pi r}\) कागज के तल के लम्बवत् नीचे की ओर (perpendicular to the plane of paper downwards) इस खण्ड से बद्ध चुम्बकीय पलवस
\(d \phi_2=\left|\overrightarrow{\mathrm{B}} \cdot d \mathrm{~A}_2\right|\left|\mathrm{B} \cdot d \mathrm{~A}_2 \cdot \cos 0^{\circ}\right|\)
या \(d \phi_2=\frac{\mu_0 I}{2 \pi r} \cdot(a \cdot d r) \cdot 1\)
\(=\frac{\mu_0 \mathrm{I} a}{2 \pi} \cdot \frac{d r}{r}\)
∴लूप से सम्बद्ध कुल चुम्बकीय फ्लक्स

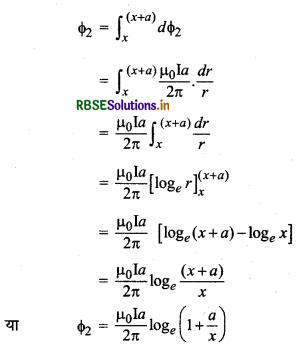
∴ अन्योन्य प्रेरकत्व
\(\mathrm{M}=\frac{\phi_2}{\mathrm{I}}=\frac{\mu_0 a}{2 \pi} \log _e\left(1+\frac{a}{x}\right)\)


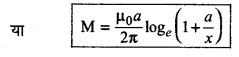
(b) लूप से सम्बद्ध चुम्बकीय फ्लक्स
\(\phi_2=\frac{\mu_0 I a}{2 \pi} \log _e\left(\frac{x+a}{x}\right)\)
∴ लूप में प्रेरित विद्युत् वाहक बल

यहाँ I =  50 A; v = 10 ms^-1;  x = 0.2 m; a = 0.1 m, e = ? 

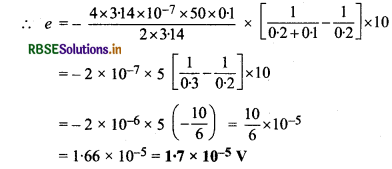
प्रश्न 17.
M द्रव्यमान तथा R त्रिज्या वाले पहिए के रिम पर एक रेखीय आवेश (linear charge) λ प्रति इकाई स्थापित किया

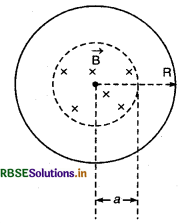
गया है। पहिए के स्पोक हल्के एवं अचालक (light and non - conducting) हैं। पहिया ऊर्ध्व अक्ष के परितः घूमने के लिए स्वतन्त्र (free to rotate) है (चित्र)। पहिए के त्रिज्य क्षेत्र (within the rim) में एकसमान चुम्बकीय क्षेत्र B व्यापित (oxtends) है जो \(\overrightarrow{\mathrm{B}}=-\mathrm{B}_0 \hat{k}\) (r \(\leq \boldsymbol{a}, a<\mathbf{R}\)) (अन्यथा) \(\overrightarrow{\mathbf{B}}\) = 0 द्वारा परिभाषित है।
चुम्बकीय क्षेत्र को अचानक बन्द (off) कर देने पर पहिए का कोणीय वेग कितना होगा?
हल: 
जब चुम्बकीय क्षेत्र को अचानक बन्द कर दिया जाता है, तो पहिए से बद्ध चुम्बकीय फ्लक्स में परिवर्तन होता है जो रिम में वि. वा. बल प्रेरित करता है तथा घूर्णन आवेश प्रदान करता है।
पहिए को दी गई ऊर्जा \(\frac{1}{2} \phi i\) है, जिसमें i घूमते हुए पहिए पर आवेश के कारण तुल्य धारा है।
यदि पहिए का जड़त्व आघूर्ण I = MR² हो तथा यह ω कोणीय वेग से घूम रहा हो तो घूर्णन ऊर्जा \(\frac{1}{2} \mathrm{I} \omega^2\) होगी, अत: ऊर्जा संरक्षण के नियम से,
\(\frac{1}{2} I \omega^2=\frac{1}{2} \phi i\) ................(1)
तुल्य धारा i = \(\frac{\dot{q}}{\mathrm{~T}}\)
∴ समी. (1) से, \(\frac{1}{2} \mathrm{MR}^2 \cdot \omega^2=\frac{1}{2} \phi \cdot \frac{q}{\mathrm{~T}}\)
या \(\frac{1}{2} \mathrm{MR}^2 \cdot \omega^2=\frac{1}{2}\left(\mathrm{~B} \pi a^2\right) \cdot \frac{2 \pi R \lambda}{2 \pi / \omega}\),  क्योंकि q = λ.2πR और T = \(2 \pi / \omega\)
या \(\mathrm{MR}^2 \omega^2=\mathrm{B} \pi a^2 \cdot \mathrm{R} \lambda \cdot \omega\)
या \(\mathrm{MR}^2 \omega=\mathrm{B} \pi a^2 \mathrm{R} \lambda\)
\(\therefore \quad \omega=\frac{\mathrm{B} \pi a^2 \mathrm{R} \lambda}{\mathrm{MR}^2}=\frac{\mathrm{B} \pi a^2 \lambda}{\mathrm{MR}}\)
या \(\omega=\frac{\pi a^2 \mathrm{~B} \lambda}{\mathrm{MR}}\) (चुम्बकीय क्षेत्र B की दिशा में)