RBSE Solutions for Class 12 Physics Chapter 5 चुंबकत्व एवं द्रव्य

Rajasthan Board RBSE Solutions for Class 12 Physics Chapter 5 चुंबकत्व एवं द्रव्य Textbook Exercise Questions and Answers.

RBSE Class 12 Physics Solutions Chapter 5 चुंबकत्व एवं द्रव्य

RBSE Class 12 Physics चुंबकत्व एवं द्रव्य Textbook Questions and Answers

प्रश्न 1.
भू - चुम्बकत्व सम्बन्धी निम्नलिखित प्रश्नों के उत्तर दीजिए-
(a) एक सदिश को पूर्णरूपेण व्यक्त (specification) करने के लिए तीन राशियों की आवश्यकता होती है। उन तीन स्वतन्त्र राशियों के नाम लिखिए जो परम्परागत (conventionally) रूप से पृथ्वी के चुम्बकीय - क्षेत्र को व्यक्त करने के लिए प्रयुक्त होती हैं।
(b) दक्षिण भारत में किसी स्थान पर नति कोण (angle of dip) का मान लगभग 18° है। ब्रिटेन में आप इससे अधिक नति कोण की अपेक्षा (expect) करेंगे या कम की?
(c) यदि आप ऑस्ट्रेलिया के मेलबोर्न शहर में भू - चुम्बकीय क्षेत्र रेखाओं का नक्शा (map) बनाएँ तो ये रेखाएँ पृथ्वी से बाहर आयेंगी या अन्दर जायेंगी (seem to go into the ground or come out of the ground)?
(d) एक चुम्बकीय सुई (compass) जो ऊर्ध्वाधर तल में घूमने के लिए स्वतन्त्र है, यदि भू - चुम्बकीय (geomagnetic) उत्तरी या दक्षिणी बुव पर रखी हो तो यह किस दिशा में संकेत करेगी? 
(e) यह माना जाता है (it is claimed) कि पृथ्वी का चुम्बकीय क्षेत्र लगभग एक चुम्बकीय द्विध्रुव के क्षेत्र जैसा है जो पृथ्वी के केन्द्र पर रखा है और जिसका द्विध्रुव आघूर्ण 8 x 10²² JT^-1 है। कोई ढंग सुझाइए (In some way) जिससे इस संख्या के परिमाण की कोटि (order of magnitude) जाँची जा सके।
(f) भूगर्भशास्त्रियों (Geologists) का मानना है कि मुख्य N - S चुम्बकीय ध्रुवों के अतिरिक्त, पृथ्वी की सतह पर कई अन्य स्थानीय घुव (local poles) भी हैं, जो विभिन्न दिशाओं में विन्यस्त (oriented) हैं। ऐसा होना कैसे सम्भव है?
उत्तर:
(a) पृथ्वी का चुम्बकीय क्षेत्र निम्न तीन राशियों द्वारा व्यक्त किया जाता है-

• दिक्पात कोण Φ (Angle of Declination) 
• नमन कोण या नति कोण θ (Angle of Dip)
• पृथ्वी के चुम्बकीय क्षेत्र का क्षैतिज घटक B_H (Horizontal Component of Earth's Magnetic Field)।

(b) चूँकि ब्रिटेन, दक्षिण भारत की तुलना में पृथ्वी के उत्तरी ध्रुव के अधिक समीप है, अत: वहाँ पर नमन कोण दक्षिण भारत में नमन कोण की तुलना में अधिक होगा। ब्रिटेन में नति कोण लगभग 70° है।

(c) ऑस्ट्रेलिया पृथ्वी के दक्षिणी गोलार्द्ध (southern hemisphere) में स्थित है और पृथ्वी के दक्षिणी ध्रुव से चुम्बकीय क्षेत्र रेखाएँ बाहर निकलती हैं, अत: ऑस्ट्रेलिया के मेलबोर्न शहर के लिए चुम्बकीय क्षेत्र रेखाओं के नक्शे में क्षेत्र रेखाएँ बाहर निकलती हुई प्रतीत होंगी।

(d) ध्रुवों पर पृथ्वी का चुम्बकीय क्षेत्र ऊर्ध्वाधर होता है। अत: वहाँ पर नति कोण का मान 90° होगा और स्वतन्त्रतापूर्वक लटकी हुई चुम्बकीय सुई (कधिर तल में घूमने के लिए स्वतन्त्र) ऊर्ध्वाधर दिशा को इंगित करेगी।

(e) पृथ्वी के चुम्बकीय द्विध्रुव के निरक्ष बिन्दु पर चुम्बकीय क्षेत्र \(\vec{B}\)
\(\overrightarrow{\mathrm{B}}=-\frac{\mu_0}{4 \pi} \frac{\vec{m}}{r^3}\) ..................(1)
यहाँ m= 8 x 10²² JT^-1, r = 6.4 x 10⁶ m 
समीकरण (1) का परिमाण,
\(\mathrm{B}=\frac{\mu_0}{4 \pi} \frac{m}{r^3}\)
= \(10^{-7} \times \frac{8 \times 10^{22}}{\left(6 \cdot 4 \times 10^6\right)} \mathrm{T}\)
= 0.3 x 10^-4 T = 0.3 G
B = 0.3 G, यह मान पृथ्वी पर प्रेक्षित क्षेत्र के परिमाण की कोटि का है।

(f) सम्भव है, यद्यपि पृथ्वी का सम्पूर्ण चुम्बकीय क्षेत्र एकल चुम्बकीय द्विध्रुव के तुल्य माना जाता है फिर भी स्थानीय N - S ध्रुव उत्पन्न हो सकते हैं जैसे कि चुम्बकित खनिज भण्डारों के कारण (due to the different deposits of magnetised materials)।

प्रश्न 2. 
निम्नलिखित प्रश्नों के उत्तर दीजिए-
(a) एक जगह से दूसरी जगह जाने पर पृथ्वी का चुम्बकीय क्षेत्र बदलता है। क्या यह समय के साथ भी बदलता है? यदि हाँ, तो कितने समयान्तराल (time scale) पर इसमें पर्याप्त (appreciably) परिवर्तन होते हैं?
(b) पृथ्वी के क्रोड में लोहा है, यह ज्ञात है। फिर भी भूगर्भशास्त्री इसको पृथ्वी के चुम्बकीय क्षेत्र का स्त्रोत नहीं मानते हैं, क्यों?
(c) पृथ्वी के क्रोड के बाहरी चालक भाग में प्रवाहित होने वाली आवेश धाराएँ (charged currents) भू - चुम्बकीय क्षेत्र के लिए उत्तरदायी समझी जाती हैं। इन धाराओं को बनाये रखने वाली बैटरी (ऊर्जा स्रोत) क्या हो सकती है?
(d) अपने 4 - 5 अरब वर्षों (billion years) के इतिहास में पृथ्वी अपने चुम्बकीय क्षेत्र की दिशा कई बार उलट चुकी होगी। भूगर्भशास्त्री इतने सुदूर अतीत (in such distant past) के पृथ्वी के चुम्बकीय क्षेत्र के बारे में कैसे जान पाते हैं?
(e) बहुत अधिक दूरियों पर (greater than about) (30000 km से अधिक) पृथ्वी का चुम्बकीय क्षेत्र अपनी द्विधुवीय आकृति (dipole shape) से काफी भिन्न हो जाता है। कौन - से कारक (what agencies) इस विकृति (distortion) के लिए उत्तरदायी हो सकते हैं?
(f) अन्तरातारकीय अन्तरिक्ष (Inter stellar space) में 10^-12 T की कोटि का बहुत ही क्षीण चुम्बकीय क्षेत्र होता है। क्या इस क्षीण चुम्बकीय क्षेत्र के भी कुछ प्रभावी परिणाम (significant consequence) हो सकते हैं? समझाइए (explain)।
उत्तर:
(a) हाँ, यह समय के साथ बदलता है। स्पष्ट दिखायी पड़ने वाले अन्तर के लिए समय अन्तराल कुछ सौ वर्ष है, लेकिन कुछ वर्षों के छोटे पैमाने पर भी इसमें होने वाले परिवर्तन पूर्णतः उपेक्षणीय नहीं हैं।

(b) भूगर्भ में पिघला हुआ लोहा (molten iron) अपने क्यूरी ताप से काफी ऊँचे ताप पर होता है। इतने ऊँचे ताप पर लोहे का लौह-चुम्बकत्व गुण अनुचुम्बकत्व में बदल जाता है, अत: भू - क्रोड में मौजूद लोहा पृथ्वी के चुम्बकत्व का स्रोत नहीं माना जा सकता है।

(c) एक सम्भावना (one possibility) पृथ्वी के अन्तरंग (outer conducting regions of earth core) में रेडियो सक्रियता है, लेकिन वास्तविकता की जानकारी किसी को नहीं है। पृथ्वी के गर्भ में उपस्थित रेडियो - ऐक्टिव पदार्थों के विघटन से प्राप्त ऊर्जा ही आवेश धाराओं की ऊर्जा का स्रोत हो सकती है।

(d) प्रारम्भ में भूगर्भ में अनेकों पिघली हुई चट्टानें (molten rocks) थी जो समय के साथ धीरे - धीरे ठोस होती चली गई। इन चट्टानों में मौजूद लौह - चुम्बकीय पदार्थं उस समय के पृथ्वी के चुम्बकीय क्षेत्र के अनुरूप संरेखित हो गये। इस प्रकार भूतकाल का भू - चुम्बकत्व इन चट्टानों में चुम्बकीय पदार्थों के अनुरूपण में अभिलेखित है। इन चट्टानों का भू - चुम्बकीय अध्ययन उस समय के पृथ्वी के चुम्बकीय क्षेत्र का ज्ञान प्रदान करता है।

(e) बहुत अधिक दूरी पर पृथ्वी के आयनमण्डल में आयनों की गति के कारण उत्पन्न चुम्बकीय क्षेत्र से पृथ्वी के चुम्बकीय क्षेत्र में परिवर्तन हो जाते हैं। आयन मण्डल में आयनों के कारण उत्पन्न चुम्बकीय क्षेत्र सौर पवन पर निर्भर करता है।

(f) सूत्र: R = \(\frac{m v}{q \mathrm{~B}}\) से, R ∝ \(\frac{1}{B}\)
स्पष्ट है कि अत्यन्त क्षीण चुम्बकीय क्षेत्र (weak magnetic field) में गतिशील आवेशित कणों के मार्ग की त्रिज्या अधिक होती है। यह मार्ग अल्प दूरी में ऋजुरेखीय प्रतीत होता है, अत: छोटी दूरियों के लिए सूक्ष्म चुम्बकीय क्षेत्र अप्रभावी प्रतीत होते हैं परन्तु बड़ी दूरियों में ये प्रभावी विक्षेपण (effective deflection) उत्पन्न करते हैं।

प्रश्न 3. 
एक छोटा छड़ चुम्बक (short bar magnet) जो एकसमान बाह्य चुम्बकीय क्षेत्र 0.25 T के साथ 30° का कोण बनाता है, पर 4.5 x 10^-2 J का बल आघूर्ण लगता है। चुम्बक के चुम्बकीय आघूर्ण का परिमाण क्या है?
हल: 
सूत्र: τ = mB sinθ ⇒ m = \(\frac{\tau}{B \sin \theta} \)
दिया है: τ = 4.5 x 10^-2 J; B = 0.25 T; θ = 30°; M = ?
\(\therefore \quad m=\frac{\tau}{\mathrm{B} \sin \theta}=\frac{4.5 \times 10^{-2}}{0.25 \times \sin 30^{\circ}}\)
या m = \(\frac{4 \cdot 5 \times 10^{-2}}{0.25 \times 0 \cdot 5}=\frac{9}{0 \cdot 25} \times 10^{-2}\)
∴ m = 36 x 10^-2 JT^-1 = 0.36 JT^-1

प्रश्न 4.
चुम्बकीय आघूर्ण M = 0.32 JT^-1 वाला एक छोटा छड़ चुम्बक, 0.15 T के एकसमान बाह्य चुम्बकीय क्षेत्र (uniform external magnetic field) में रखा है। यदि यह छड़ क्षेत्र के तल में घूमने के लिए स्वतन्त्र हो, तो क्षेत्र के किस विन्यास में यह (i) स्थायी सन्तुलन और (ii) अस्थायी सन्तुलन में होगी? प्रत्येक स्थिति में चुम्बक की स्थितिज ऊर्जा का मान बताइए।
हल: 
दिया है: M = 0.32 JT^-1; B = 0.15 T
(i) जब चुम्बक की अक्ष बाह्य चुम्बकीय क्षेत्र के साथ संरेखित होगी अर्थात् जब θ = 0 तो चुम्बक की यह स्थिति स्थायी सन्तुलन को व्यक्त करेगी; क्योंकि यदि चुम्बक को इस स्थिति से थोड़ा कोणीय विस्थापन (angular displacement) देकर छोड़ दिया जाये तो चुम्बक घूर्णन करके पुनः अपनी पूर्व स्थिति में पहुँच जायेगी। 
∵ चुम्बक की स्थितिज ऊर्जा
U = -MB cosθ
∴ स्थायी सन्तुलन में,
U = -0.32 x 0.15 x cos0 
= -0.32 x 0.15 x 1
= -0.0480 J
= -4.8 x 10^-2 J

(ii) जब चुम्बक की अक्ष बाह्य चुम्बकीय क्षेत्र के साथ विपरीत दिशा (opposite direction) में संरेखित होगी (अर्थात् θ = 180°) तो यह चुम्बक की अस्थायी साम्यावस्था (unstable equilibrium) होगी क्योंकि यदि इस स्थिति से चुम्बक को थोड़ा कोणीय विस्थापन दे दिया जाये, तो वह घूमकर अपनी स्थायी साम्यावस्था में पहुँच जायेगा और अस्थायी साम्यावस्था में नहीं पहुँचेगा। 
∵ U = - MB cosθ
∴ U = -0.32 x 0.15 x cos 180° 
= +0.048 J
= +4.8 x 10^-2 J 

प्रश्न 5. 
एक परिनालिका में पास - पास लपेटे गये 800 फेरे हैं तथा इसकी अनुप्रस्थ काट का क्षेत्रफल 2.5 x 10^-4 m² है और इसमें 3.0 A धारा प्रवाहित हो रही है। समझाइए कि किस अर्थ में यह परिनालिका एक छड़ चुम्बक की तरह व्यवहार करती है? इसके साथ जुड़ा हुआ चुम्बकीय आघूर्ण कितना है? 
हल: 
दिया है: N = 800; i = 3.0 A; A = 2.5 x 10^-4 m²
∴ चुम्बकीय आघूर्ण, M = NIA
= 800 x 3.0 x 2.5 x 10^-4
= 0.60 JT^-1
धारावाही परिनालिका को स्वतन्त्रतापूर्वक किसी समरूप चुम्बकीय क्षेत्र (uniform magnetic field) में लटकाया जाये तो दण्ड चुम्बक की भौति ही परिनालिका की अक्ष बाहरी चुम्बकीय क्षेत्र के साथ संरेखित हो जाती है अर्थात् दण्ड चुम्बक की भाँति परिनालिका पर भी चुम्बकीय क्षेत्र में एक बलयुग्म कार्य करता है। इस प्रकार धारावाही परिनालिका दण्ड चुम्बक की भांति व्यवहार करती है।

प्रश्न 6. 
यदि प्रश्न 5 में बताई गई परिनालिका ऊर्ध्वाधर दिशा के परितः घूमने के लिए स्वतन्त्र हो और इस पर क्षैतिज दिशा में एक 0.25 T का एक समान चुम्बकीय क्षेत्र लगाया जाए, तो इस परिनालिका पर लगने वाले बलयुग्म के आघूर्ण का मान उस समय क्या होगा, जब इसकी अक्ष आरोपित क्षेत्र की दिशा से 30° का कोण बना रही हो? 
हल: 
दिया है: B = 0.25 T; M = 0.60 JT^-1; θ = 30°; τ = ? 
∴ परिनालिका पर लगने वाले बलयुग्म का आघूर्ण
τ = MB sinθ = 0.60 x 0.25 x sin 30°
या τ =  0.60 x 0.25 x \(\frac{1}{2}\) = 0.30 x 0.25 
∴ τ = 0.075 J =  7.5 x 10^-2 J 

प्रश्न 7. 
एक छड़ चुम्बक जिसका चुम्बकीय आघूर्ण 1.5 JT^-1 है, 0.22 T के एकसमान चुम्बकीय क्षेत्र के अनुदिश रखा है।
(a) एक बाह्य बल आघूर्ण कितना कार्य करेगा यदि यह चुम्यक को चुम्बकीय क्षेत्र के (i) लम्बवत्, (ii) विपरीत दिशा में संरेखित (aligned) करने के लिए घुमा दे।
(b) स्थिति (i) एवं (ii) में चुम्बक पर कितना बल आघूर्ण होता है?
हल: 
दिया है: M = 1.5 JT^-1; B = 0.22 T 
(a) द्विध्रुव को घुमाने में कृत कार्य
W = MB (cosθ₁ - cosθ₂)
(i) θ₁ = 0, θ₂ = 90°
∴ W = 1.5 x 0.22 (cos0° - cos 90°)
= 1.5 x 0.22 (1 - 0)
= 0.330 J

(ii)  θ1 = 0°, θ2 = 180°
∴ W = 1.5 x 0.22 (cos0° - cos 180°)
= 0.33 [ 1 - (-1) ]
= 0.33 x 2 
= 0.66 J

(b) (i) स्थिति (ii) में, θ = 90° 
∴ चुम्बक पर लगने वाले बलयुग्म का आपूर्ण 
∴ τ = MB sinθ = MB sin 90° = MB
τ = 1.5 x 0.22 = 0.33 J 
(ii) स्थिति (ii) में θ = 180° 
∴ sinθ - sin 180° = 0 
अतः τ = MB sinθ  = 0 (शून्य)

प्रश्न 8. 
एक परिनालिका जिसमें पास - पास 2000 फेरे लपेटे गये हैं तथा जिसके अनुप्रस्थ काट का क्षेत्रफल 1.6 x 10^-4 m² है और जिसमें 4.0 A की धारा प्रवाहित हो रही है, इसके केन्द्र से इस प्रकार लटकाई (suspended) गई है कि यह एक क्षैतिज तल (horizontal plane) में घूम सके।
(a) परिनालिका के चुम्बकीय आघूर्ण का मान क्या है?
(b) परिनालिका पर लगने वाला बल एवं बल आघूर्ण (force and torque) क्या है, यदि इस पर इसकी अक्ष से 30° का कोण बनाता हुआ 7.5 x 10^-2 T का एकसमान क्षैतिज चुम्बकीय क्षेत्र लगाया जाये? 
हल: 
दिया है: N = 2000, A = 1.6 x 10^-4 m²
धारा I = 4.0 A, B = 7.5 x 10^-2 T 
(a) परिनालिका का चुम्बकीय आघूर्ण
M = NIA
= 2000 x 4.0 x 1.6 x 10^-4 
= 8 x 1.6 x 10^-1 
= 1.28 Am²

(b) सूत्र: τ = MB sinθ
= 1.28 x 7.5 x 10^-2 sin 30
= 1.28 x 7.5 x 10^-2 \(\times \frac{1}{2}\) 
= 0.64 x 7.5 x 10^-2
= 4.8 x 10^-2 Nm = 0.048 Nm 
∵ परिनालिका का अनुप्रस्थ क्षेत्रफल समान है, अत: दोनों ध्रुवों पर बलों के परिमाण समान होंगे।
∴ नेट बल = 0 (शून्य)

प्रश्न 9. 
एक वृत्ताकार कुण्डली (circular coil) जिसमें 16 फेरे हैं और त्रिज्या 10 cm है तथा जिसमें 0.75 A धारा प्रवाहित हो रही है, इस प्रकार रखी है कि इसका तल 5.0 x 10^-2 T परिमाण वाले बाह्य क्षेत्र के लम्बवत् है। कुण्डली, चुम्बकीय क्षेत्र के लम्बवत् और इसके अपने तल में स्थित एक अक्ष के चारों तरफ घूमने के लिए स्वतन्त्र है। यदि कुण्डली को जरा - सा घुमाकर (turned slightly) छोड़ दिया जाये तो यह अपनी स्थायी सन्तुलनावस्था (stable equilibrium) के इधर - उधर 2.0 s^-1 की आवृत्ति से दोलन करती है। कुण्डली का अपने घूर्णन अक्ष के परितः जड़त्व आघूर्ण क्या है?
हल: 
दिया है: N= 16; r = 10 cm = 0.10 m; i = 0.75 A; B = 5.0 x 10^-2 T; आवृत्ति n = 2.0s^-1; जड़त्व आघूर्ण I =? 
∴ कुण्डली के तल का क्षेत्रफल
A = πr² 
= 3.14 x 0.1 x 0.1
= 3.14 x 10^-2 m 
कुण्डली का चुम्बकीय द्विध्रुव आघूर्ण
M =NIA
= 16 x 0.75 x 3.14 x 10^-2
= 37.68 x 10^-2 = 0.3768 = 0.377Am²
∵चुम्बकीय क्षेत्र में चुम्बकीय द्विध्रुव के दोलनों का आवर्तकाल
T = \(2 \pi \sqrt{\frac{\mathrm{I}}{\mathrm{MB}}}\) या \(\mathrm{T}^2=4 \pi^2 \frac{\mathrm{I}}{\mathrm{MB}}\)
या \(\frac{1}{\mathrm{~T}^2}=\frac{\mathrm{MB}}{4 \pi^2 \mathrm{I}}\)
या \(n^2=\frac{\mathrm{MB}}{4 \pi^2 \mathrm{I}}\)
∴ I = \(\frac{\mathrm{MB}}{4 \pi^2 n^2}=\frac{0.377 \times 5.0 \times 10^{-2}}{4 \times 9.86 \times 4}\)
= 0.0119 x 10^-2
= 1.2 x 10^-4 kg m²

प्रश्न 10. 
एक चुम्बकीय सुई चुम्बकीय याम्योत्तर के समान्तर एक ऊर्ध्वाधर तल (vertical plane) में घूमने के लिए स्वतन्त्र है। इसका उत्तरी ध्रुव क्षैतिज से 22° के कोण पर नीचे की ओर झुका है। इस स्थान पर चुम्बकीय क्षेत्र के क्षैतिज अवयव का मान 0.35 G है। इस स्थान पर पृथ्वी के चुम्बकीय क्षेत्र का परिमाण ज्ञात कीजिए।
हल: 
दिया है: नति कोण (angle of dip) θ = 22°;  चुम्बकीय क्षेत्र का क्षैतिज घटक H = 0.35 G = 0.35 x 10^-4 T; B = ? 
\(\because \quad \mathrm{B}_{\mathrm{H}}=\mathrm{B} \cos \theta \Rightarrow \mathrm{B}=\frac{\mathrm{B}_{\mathrm{H}}}{\cos \theta}\)
∴\(\mathrm{B}=\frac{0.35 \times 10^{-4}}{\cos 22^{\circ}}\)
= \(\frac{0.35 \times 10^{-4}}{0.9272}\)
= 0.38 x 10^-4 T = 0.38 G

प्रश्न 11. 
दक्षिण अफ्रीका में किसी स्थान पर एक चुम्बकीय सुई भौगोलिक उत्तर से 12° पश्चिम (12° west) की ओर संकेत करती है। चुम्बकीय याम्योत्तर में सरेखित (aligned) नति वृत्त की चुम्बकीय सुई का उत्तरी ध्रुव क्षैतिज से 60° उत्तर की ओर संकेत करता है। पृथ्वी के चुम्बकीय क्षेत्र का क्षैतिज घटक मापने पर 0.16 G पाया जाता है। इस स्थान पर पृथ्वी के क्षेत्र का परिमाण और दिशा बताइए।
हल: 
नति कोण θ = 60°, जब दिकपात कोण (declination) Φ = 12° उत्तर से पश्चिम की ओर
B_H = 0.16 G
∵ B_H = B cosθ ⇒ B = \(\frac{\mathrm{B}_{\mathrm{H}}}{\cos \theta}\)
∴ B = \(\frac{0.16}{\cos 60^{\circ}}=\frac{0 \cdot 16}{1 / 2}\) = 0.16 x 2 = 0.32 G
अत: इस स्थान पर पृथ्वी का परिणामी चुम्बकीय क्षेत्र 0.32 G है जिसकी दिशा भौगोलिक याम्बोत्तर (Geographical meridian) से 12° पश्चिम की ओर क्षैतिज से 60° के कोण पर ऊपर की ओर है।

प्रश्न 12. 
किसी छोटे छड़ चुम्बक का चुम्बकीय आघूर्ण 0.48 JT^-1 है। चुम्बक के केन्द्र से 10 cm की दूरी पर स्थित किसी बिन्दु पर इसके चुम्बकीय क्षेत्र का परिमाण एवं दिशा बताइए यदि यह बिन्दु (i) चुम्बक के अक्ष पर स्थित हो, (ii) चुम्बक के अभिलम्बवत् समद्विभाजक (equatorial line of the magnet) पर स्थित हो।
हल: 
दिया है: m = 0.48 JT^-1; r = 0.10 m; B =? 
(i) जब बिन्दु अक्षीय स्थिति (axial position) में हो, तो
\(\mathrm{B}_{a x}=\frac{\mu_0}{4 \pi} \cdot \frac{2 \mathrm{M}}{r^3}\)
=\(10^{-7} \times \frac{2 \times 0.48}{(0 \cdot 10)^3}\)
= 9.6 x 10^-5 T = 0.96 G (दक्षिणी ध्रुव से उत्तरी ध्रुव की ओर) 

(ii) जब बिन्दु निरक्षीय स्थिति (equatorial line) में हो, तो
\(\mathrm{B}_{e q}=\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{M}}{r^3}\)
= \(\frac{1}{2} \times \frac{\mu_0}{4 \pi} \cdot \frac{2 \mathrm{M}}{r^3}\)
या \(\mathrm{B}_{e q}=\frac{\mathrm{B}_{a x}}{2}=\frac{9 \cdot 6}{2} \times 10^{-5}\)
∴ B_eq = 4.8 x 10^-5 T
= 0.48 x 10^-4 T = 0.48 G (उत्तरी ध्रुव से दक्षिणी ध्रुव की ओर) 

प्रश्न 13. 
क्षैतिज तल में रखे एक छोटे छड़ चुम्बक का अक्ष, चुम्बकीय उत्तर - दक्षिण दिशा के अनुदिश है सन्तुलन बिन्दु (उदासीन बिन्दु) चुम्बक के अक्ष पर, इसके केन्द्र से 14 cm दूर स्थित है। इस स्थान पर पृथ्वी का चुम्बकीय क्षेत्र 0.36 G एवं नति कोण शून्य है। चुम्बक के अभिलम्ब समद्विभाजक (normal bisector) पर इसके केन्द्र से उतनी ही दूर (14 cm) स्थित किसी बिन्दु पर परिणामी चुम्बकीय क्षेत्र क्या होगा ?
हल: 
दिया है: पृथ्वी का चुम्बकीय क्षेत्र B_H = 0.36 G
नति कोण θ = 0°; अक्ष पर उदासीन बिन्दु की दूरी r = 0.14 m

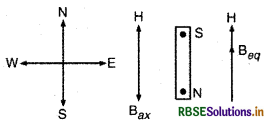
माना उदासीन बिन्दु पर चुम्बक का अक्षीय क्षेत्र B_ax है, अतः सन्तुलन बिन्दु पर,
B_ax = H
या B_ax = B cos θ = B क्योंकि θ = 0 ∴ cosθ = 1 
ये दोनों क्षेत्र दिशा में विपरीत एवं परिमाण में समान होंगे। 
या B_ax = B 
समान दूरी पर निरक्षीय स्थिति में चुम्बकीय क्षेत्र
B_eq = \(\frac{1}{2} \mathrm{~B}_{a x}=\frac{1}{2} \mathrm{~B}\)
∵ चुम्बक की निरक्षीय स्थिति में B_eq एवं H समान दिशा में होंगे, अतः यहाँ परिणामी चुम्बकीय क्षेत्र 
B_R = B_eq + H
= B_eq + B
= \(\frac{1}{2} \mathrm{~B}+\mathrm{B}\)
∴ B_R = \(\frac{3}{2} B=\frac{3}{2}\) x 0.36 = 0.54 G (इसकी दिशा पृथ्वी के चुम्बकीय क्षेत्र के अनुदिश होगी।)

प्रश्न 14. 
यदि प्रश्न 13 में वर्णित चुम्बक को 180° से घुमा दिया जाये, तो सन्तुलन बिन्दुओं की नई स्थिति क्या होगी?
हल: 
चुम्बक को 180° से घुमा देने पर चुम्बक का दक्षिणी ध्रुव भौगोलिक दक्षिण दिशा में होगा। उदासीन बिन्दु अब निरक्षीय रेखा पर मिलेगा। 
अक्षीय स्थिति में उदासीन बिन्दु हेतु,
H = B_ax = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \mathrm{M}}{r_{a x}^3}\)
या \(r_{a x}^3=\frac{\mu_0}{4 \pi} \cdot \frac{2 m}{\mathrm{~B}_{a x}}\)
\(\therefore \quad r_{a x}=\left[\frac{\mu_0}{4 \pi} \cdot \frac{2 m}{\mathrm{~B}_{a x}}\right]^{1 / 3}\)
\(=\left[\frac{\mu_0}{4 \pi} \cdot \frac{2 m}{H}\right]^{1 / 3}\)
निरक्षीय स्थिति में सन्तुलन बिन्दु के लिए,
H = B_eq = \(\frac{\mu_0}{4 \pi} \cdot \frac{m}{r_{e q}^3}\)
⇒ r_eq³ = \(\frac{\mu_0}{4 \pi} \cdot \frac{m}{\mathrm{~B}_{e q}}\)
या r_eq³ = \(\frac{\mu_0}{4 \pi} \cdot \frac{m}{H}\)
\(=\frac{1}{2} \cdot \frac{\mu_0}{4 \pi} \cdot \frac{2 m}{H}=\frac{1}{2} r_{a x}^3\)
या r_eq³ = \(\frac{1}{2} r_{a x}^3\)
या r_eq³ = \(\frac{r_{a x}}{(2)^{1 / 3}}\) ∵ r_ax = 0.14m
∴ r_eq =\( \frac{0 \cdot 14}{(2)^{1 / 3}}=\frac{0 \cdot 14}{1 \cdot 2599}=0.1111 \mathrm{~m}\)
∴ r_eq = 11.11 x 10^-2 = 11.11 cm
अतः सन्तुलन बिन्दु निरक्षीय (equatorial) स्थिति में 11.11 cm को दूरी पर प्राप्त होगा।

प्रश्न 15. 
एक छोटा छड़ चुम्बक जिसका चुम्बकीय आघूर्ण 5.25 x 10^-2 JT^-1 है, इस प्रकार रखा है कि इसका अक्ष पृथ्वी के क्षेत्र की दिशा के लम्बवत् है। चुम्बक के केन्द्र से कितनी दूरी पर परिणामी क्षेत्र पृथ्वी के क्षेत्र की दिशा से 45° का कोण बनायेगा, यदि हम (a) अभिलम्ब समद्विभाजक (its normal bisector) पर देखें, (b) अक्ष पर (its axis) देखें। इस स्थान पर पृथ्वी के चुम्बकीय क्षेत्र का परिमाण 0.42 G है। प्रयुक्त दूरियों की तुलना में चुम्बक की लम्बाई की उपेक्षा कर सकते हैं।
हल: 
दिया है: m = 5.25 x 10^-2 JT^-1;
पृथ्वी का क्षेत्र B_H = 0.42 G = 0.42 x 10^-4 T

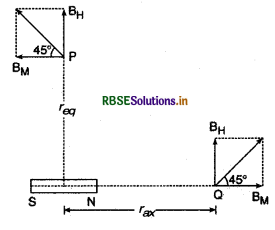
(a) माना चुम्बक के केन्द्र से req दूरी पर चुम्बक के क्षेत्र से परिणामी चुम्बकीय क्षेत्र 45° का कोण बनाता है, अतः इस बिन्दु पर,
B_M = \(\frac{\mu_0}{4 \pi} \cdot \frac{m}{r_{e q}^3}\)
∵ tan 45° = \(\frac{\mathrm{B}_{\mathrm{H}}}{\mathrm{B}_{\mathrm{M}}}\)
या B_H = B_M tan 45° = B_M = \(\frac{\mu_0}{4 \pi} \cdot \frac{m}{r_{e q}^3}\)
∴ r_eq³ = \(\frac{\mu_0}{4 \pi} \cdot \frac{m}{\mathrm{~B}_{\mathrm{H}}}\)
or r_eq = \(\left[\frac{\mu_0}{4 \pi} \cdot \frac{m}{B_H}\right]^{1 / 3}\)
= \(\left[10^{-7} \times \frac{5 \cdot 25 \times 10^{-2}}{0 \cdot 42 \times 10^{-4}}\right]^{1 / 3}\)
= 5 x 10^-2 m
= 5 cm

(b) अक्षीय बिन्दु के लिए,
B_M = \(\frac{\mu_0}{4 \pi}, \frac{2 m}{r_{a x}^3}\)
पुन: \(\frac{\mathrm{B}_{\mathrm{H}}}{\mathrm{B}_{\mathrm{M}}}=\tan 45^{\circ}\) = 1 ⇒ B_M = B_H
∴ B_H = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 m}{r_{a x}^3}\)
⇒ r_ax³ = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 m}{\mathrm{~B}_{\mathrm{H}}}\)
∴ r_ax = \(\left[\frac{\mu_0}{4 \pi}, \frac{2 m}{B_H}\right]^{1 / 3}\)
= 2 ^1/3 \(\left[\frac{\mu_0}{4 \pi} \cdot \frac{m}{\mathrm{~B}_{\mathrm{H}}}\right]^{1 / 3}\)
= 2 ^1/3 x r_eq
= 2^1/3 x 5 x 10^-2 m
= 1.2599 x 5 x 10^-2 m
= 6.3 cm

प्रश्न 16. निम्नलिखित प्रश्नों के उत्तर दीजिए-
(a) ठण्डा करने पर किसी अनुचुम्बकीय पदार्थ का नमूना अधिक चुम्बकन (greater magnetisation) क्यों प्रदर्शित करता है ? (एक ही चुम्बककारी क्षेत्र के लिए)
(b) अनुचुम्बकत्व के विपरीत, प्रतिचुम्बकत्व पर ताप का प्रभाव लगभग नहीं होता, क्यों?
(c) यदि एक टोरॉइड में बिस्मथ का क्रोड लगाया जाये तो इसके अन्दर चुम्बकीय क्षेत्र उस स्थिति की तुलना में (किंचित) कम (slightly lesser) होगा या (किंचित) ज्यादा (slightly greater) होगा, जबकि क्रोड खाली हो?
(d) क्या किसी लौह - चुम्बकीय पदार्थ कीचुम्बकशीलता चुम्बकीय क्षेत्र पर निर्भर करती है? यदि हाँ, तो उच्च चुम्बकीय क्षेत्रों के लिए इसका मान कम होगा या अधिक?
(e) किसी लौह चुम्बक की सतह के प्रत्येक बिन्दु पर चुम्बकीय क्षेत्र रेखाएँ सदैव लम्बवत् होती हैं। [यह तथ्य उन स्थिर विद्युत् क्षेत्र रेखाओं के सदृश है जो चालक की सतह के प्रत्येक बिन्दु पर लम्बवत् होती है] क्यों?
(f) क्या किसी अनुचुम्बकीय नमूने का अधिकतम सम्भव चुम्बकन, लौह चुम्बक के चुम्बकन के परिमाण की कोटि का होगा?
उत्तर:
(a) ताप के घटने पर अनुचुम्बकीय पदार्थ के परमाणु चुम्बकों का ऊष्मीय विक्षोभ (thermal motion) कम हो जाता है; फलस्वरूप किसी बाहरी चुम्बकीय क्षेत्र में क्षेत्र के साथ उनका संरेखण बढ़ जाता है जो ताप कम होने के साथ - साथ बढ़ता रहता है। इसीलिए ठण्डा करने पर अनुचुम्बकीय पदार्थ अधिक चुम्बकन प्रदर्शित करते हैं।

(b) प्रतिचुम्बकीय पदार्थ के नमूने में प्रेरित चुम्बकीय आघूर्ण सदैव बाहरी चुम्बकीय क्षेत्र की विपरीत दिशा में होता है, भले ही पदार्थ के अन्दर परमाणुओं की गति कैसी भी हो। इस प्रकार प्रतिचुम्बकत्व पर ताप का प्रभाव नहीं होता है।

(c) चूँकि प्रतिचुम्बकीय पदार्थों की उपस्थिति में बाहरी चुम्बकीय क्षेत्र का मान घट जाता है और बिस्मथ प्रतिचुम्बकीय पदार्थ है। इसलिए टोरॉइड के अन्दर बिस्मथ-क्रोड रखने पर चुम्बकीय क्षेत्र कुछ कम हो जायेगा।

(d) लौह - चुम्बकीय पदार्थों की चुम्बकशीलता बाह्य चुम्बकीय क्षेत्र पर निर्भर करती है तथा तीव्र चुम्बकीय क्षेत्र के लिए इसका मान कम होता है।

(e) जब दो माध्यम किसी स्थान पर मिलते हैं और एक के लिए µ >>1 हो, तो दोनों के सम्पर्क पृष्ठ पर क्षेत्र रेखाएँ लम्बवत् हो जाती हैं।

(f) हाँ; किसी अनुचुम्बकीय पदार्थ का अधिकतम सम्भव चुम्बकत्व (संतृप्त चुम्बकत्व) लौह - चुम्बकीय पदार्थ के चुम्बकन की कोटि का हो सकता है, परन्तु अनुचुम्बकीय पदार्थ को इस कोटि तक चुम्बकित करने के लिए अत्यन्त उच्च चुम्बकन क्षेत्र की आवश्यकता होगी जो व्यावहारिक रूप से प्राप्त करना सम्भव नहीं है।

प्रश्न 17. 
निम्नलिखित प्रश्नों के उत्तर दीजिए
(a) लौह - चुम्बकीय पदार्थ के चुम्बकन वक्र की अनुत्क्रमणीयता, डोमेनों के आधार पर गुणात्मक दृष्टिकोण से समझाइए।
(b) नर्म लोहे के एक टुकड़े के शैथिल्य लूप का क्षेत्रफल कार्बन-स्टील के टुकड़े के शैथिल्य लूप के क्षेत्रफल से कम होता है। यदि पदार्थ को बार - बार चुम्बकन चक्र से गुजारा जाये तो कौन - सा टुकड़ा अधिक ऊष्मीय ऊर्जा का क्षय करेगा?
(c) “लौह चुम्बक जैसा शैथिल्य लूप प्रदर्शित करने वाली कोई प्रणाली स्मृति संग्रहण की युक्ति है।" इस कथन की व्याख्या कीजिए।
(d) कैसेट के चुम्बकीय फीतों पर परत चढ़ाने के लिए या आधुनिक कम्प्यूटर में स्मृति संग्रहण के लिए किस तरह के लौह - चुम्बकीय पदार्थों का इस्तेमाल होता है?
(e) किसी स्थान को चुम्बकीय क्षेत्र से परिरक्षित करना है। कोई विधि सुझाइए।
उत्तर:
(a) बाह्य चुम्बकीय क्षेत्र में रखने पर डोमेनों का संरेखण होने से लौह - चुम्बकीय पदार्थों में चुम्बकत्व उत्पन्न हो जाता है। बाहरी क्षेत्र शून्य कर देने पर भी डोमेनों का संरेखण पूर्णत: समाप्त नहीं होता है अर्थात् वे अपनी प्रारम्भिक स्थिति में नहीं लौट पाते है, अत: उनमें कुछ चुम्बकन शेष रह जाता है। इसीलिए लौह - चुम्बकीय पदार्थों का चुम्बकन वक्र अनुत्क्रमणीय (irreversible) होता है।

(b) शैथिल्य लूप का क्षेत्रफल एक पूर्ण चक्र में होने वाली ऊर्जा हानि को व्यक्त करता है। यह ऊर्जा में हानि ऊष्मा (heat) में बदल जाती है। चूंकि नर्म लोहे के शैथिल्य लुप की अपेक्षा कार्बन - स्टील के शैथिल्य लूप का क्षेत्रफल अधिक होता है, अत: कार्बन - स्टील में ऊष्मा अधिक उत्पन्न होगी अर्थात् यह टुकड़ा ऊष्मीय ऊर्जा का अधिक क्षय करेगा।

(c) किसी लौह चुम्बक का चुम्बकन चुम्बककारी क्षेत्र का एकमानी फलन (single valued function) नहीं है। एक विशिष्ट क्षेत्र के लिए इसका मान चुम्बकन के इतिहास पर भी निर्भर करता है (अर्थात् कितने चुम्बकन चक्रों से गुजर चुका है आदि)। दूसरे शब्दों में कहें, तो चुम्बकन का मान, चुम्बकन चक्रों की स्मृति का अभिलेख है। यदि हर चक्र को सूचना बिट (information bits) के संगत बना दें तो शैथिल्य लूप प्रदर्शित करने वाली ऐसी व्यवस्था सूचना संग्रह करने वाली युक्ति (information storing devices) की तरह कार्य करेगी।

(d) इस कार्य के लिए सिरेमिक (विशेष रूप से संसाधित (specially treated) बैरियम लौह ऑक्साइड) पदार्थों जिन्हें फेराइट्स भी कहते हैं, का प्रयोग किया जाता है।

(e) किसी स्थान को चुम्बकीय क्षेत्र से परिरक्षित (shielding) करने के लिए उस स्थान को नर्म लोहे के छल्लों (रिंगों) से घेर दिया जाता है। ऐसा करने से चुम्बकीय बल रेखाएँ नर्म लोहे के रिंगों से होकर गुजर जाती हैं और रिंग के अन्दर प्रवेश नहीं कर पाती हैं जिससे घिरा हुआ क्षेत्र चुम्बकीय क्षेत्र से मुक्त रहेगा।

प्रश्न 18.
एक लम्बे, सीधे, क्षैतिज केबिल (horizontal eable) में 2.5 A धारा, 10° दक्षिण - पश्चिम से 10° उत्तर - पूर्व की ओर प्रवाहित हो रही है। इस स्थान पर चुम्बकीय याम्योत्तर (magnetie meridian) भौगोलिक याम्योत्तर (geographical meridian) के 10° पश्चिम में है। यहाँ पृथ्वी का चुम्बकीय क्षेत्र 0.33 G एवं नति कोण शून्य है। उदासीन बिन्दुओं की रेखा निर्धारित कीजिए। (केबिल की मोटाई की उपेक्षा कर सकते है।)
(उदासीन बिन्दुओं पर, धारावाही केबिल द्वारा चुम्बकीय क्षेत्र, पृथ्वी के क्षैतिज घटक के चुम्बकीय क्षेत्र के समान एवं विपरीत दिशा में होता है।)
हल: 
दिया है: पृथ्वी का चुम्बकीय क्षेत्र Be = 0.33 G; धारा I = 2.5 A; नतिकोण θ = 0°
∴ पृथ्वी के चुम्बकीय क्षेत्र का क्षैतिज घटक
B_H = B_e cos 0
= B = 0.33 G
= 0.33 x 10^-4 T 
ऊय घटक B_v = B_e sin 0 = 0

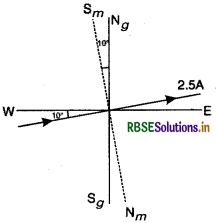
माना उदासीन बिन्दु (neutral point) की दूरी केबिल से r है, अत: r दूरी पर केबिल के कारण उत्पन्न चुम्बकीय क्षेत्र की तीव्रता
B_C = \(\frac{\mu_0}{2 \pi} \frac{I}{r}\)
∵उदासीन बिन्दु पर केबिल के कारण उत्पन्न चुम्बकीय क्षेत्र पृथ्वी के चुम्बकीय क्षेत्र के क्षैतिज घटक के परिमाण के बराबर एवं दिशा में विपरीत होगा, अतः
B_C = B_H = \(\Rightarrow \frac{\mu_0}{2 \pi} \frac{\mathrm{I}}{r}=\mathrm{B}_{\mathrm{H}}\)
\(\therefore \quad r=\frac{\mu_0}{2 \pi} \frac{\mathrm{I}}{\mathrm{B}_{\mathrm{H}}}=\frac{\mu_0}{4 \pi} \frac{2 \mathrm{I}}{\mathrm{B}_{\mathrm{H}}}\)
\(\therefore \quad r=\frac{10^{-7} \times 2 \times 2.5}{0.33 \times 10^{-4}}\)
= 15.15 x 10^-3 m
= 1.5 x 10^-2 m = 1.5 cm
उदासीन बिन्दुओं की रेखा केबिल के समान्तर ऊपर की ओर 1.5 cm दूर है।

प्रश्न 19.
किसी स्थान पर टेलीफोन केबिल में चार लम्बे, सीधे क्षैतिज तार हैं, जिनमें प्रत्येक में 1.0 A की धारा पूर्व से पश्चिम की ओर प्रवाहित हो रही है। इस स्थान पर पृथ्वी का चुम्बकीय क्षेत्र 0.39 G एवं नति कोण 35° है। दिकपात कोण लगभग शून्य है। केबिल के 4.0 cm नीचे और 40 cm ऊपर परिणामी चुम्बकीय क्षेत्रों के मान क्या होंगे?
हल: 
दिया है: पृथ्वी का चुम्बकीय क्षेत्र Be = 0.39 G 
नति कोण θ = 35°
(i) केबिल के नीचे क्षैतिज तारों के कारण उत्पन्न चुम्बकीय क्षेत्र
B₁ = \(4 \times \frac{\mu_0}{2 \pi} \frac{I}{r}=4 \times \frac{\mu_0}{4 \pi} \frac{2 \mathrm{I}}{r}\)     

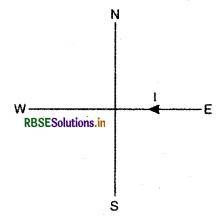
दिया है: I = 1.0 A; T = 40 cm = 4.0 x 10^-2 m
∴ B₁ = \(4 \times 10^{-7} \times \frac{2 \times 1.0}{4.0 \times 10^{-2}}\)
= 2.0 x 10^-5 T (\(\overrightarrow{\mathrm{NS}}\) दिशा में)
= 0.2 x 10^-4 T = 0.2 G 
पृथ्वी के चुम्बकीय क्षेत्र का क्षैतिज घटक दक्षिण से उत्तर की ओर (\(\overrightarrow{\mathrm{SN}}\) दिशा में) है। 
∵ H = B_e cosθ
= 0.39 cos 35°
= 0.39 x 0.82 = 0.32 G 
∴ केविल के नीचे परिणामी चुम्बकीय क्षेत्र B_H = H - B₁, क्योंकि H व B₁ की दिशाएँ विपरीत है और H > B₁
= 0.32 - 0.20 = 0.12 G 
इसी स्थान पर पृथ्वी के चुम्बकीय क्षेत्र का ऊर्ध्व घटक
B_V = B_e sinθ
= 0.39 sin 35°
=0.39 x 0.57 = 0.22 G 
अतः केबिल के नीचे परिणामी चुम्बकीय क्षेत्र
\(\begin{aligned} \mathrm{B}_{\mathrm{R}} &=\sqrt{\mathrm{B}_{\mathrm{H}}{ }^2+\mathrm{B}_{\mathrm{V}}^2} \\ &=\sqrt{(0 \cdot 12)^2+(0 \cdot 22)^2}=0 \cdot 25 \mathrm{G} \end{aligned}\)
यदि परिणामी चुम्बकीय क्षेत्र का क्षैतिज के साथ कोण δ हो, तो
tan δ = \(\frac{\mathrm{B}_{\mathrm{V}}}{\mathrm{B}_{\mathrm{H}}}=\frac{0 \cdot 22}{0 \cdot 12}\) = 1.8333
∴δ = tan^-1 (1.8333) = 61.4°

(ii) केबिल के ऊपर (r = 4.0 cm) केबिल के कारण उत्पन्न चुम्बकीय क्षेत्र (B₂) \(\overrightarrow{\mathrm{SN}}\) दिशा में होगा, अतः\( \overrightarrow{\mathrm{H}} \text { व } \overrightarrow{\mathrm{B}}_2\) जुड़ जायेंगे।
B_H = H + B₂
= 0.32 + 0.20 = 0.52 G
और B_V = 0.22 G
∴ परिणामी चुम्बकीय क्षेत्र
\(\mathrm{B}_{\mathrm{R}}=\sqrt{\mathrm{B}_{\mathrm{H}}^2+\mathrm{B}_{\mathrm{V}}{ }^2}\)
\(=\sqrt{(0.52)^2+(0.22)^2}=0.57 \mathrm{G}\)
परिणामी चुम्बकीय क्षेत्र यदि क्षैतिज के साथ δ' कोण बनाता है, तो
tan δ' = \(\frac{\mathrm{B}_{\mathrm{V}}}{\mathrm{B}_{\mathrm{H}}}=\frac{0.22}{0.52}\) = 0.4230 G
∴ δ' = tan^-1 (0.4230) = 22.9°

प्रश्न 20. 
एक चुम्बकीय सुई जो क्षैतिज तल में घूमने के लिए स्वतन्त्र है, 30 फेरों एवं 12 cm त्रिज्या वाली एक कुण्डली के केन्द्र पर रखी है। कुण्डली ऊर्ध्वाधर तल में है और चुम्बकीय याम्योत्तर से 45° का कोण बनाती है। जब कुण्डली में 0.35 A धारा प्रवाहित होती है, चुम्बकीय सुई पश्चिम से पूर्व की ओर संकेत करती है।
(a) इस स्थान पर पृथ्वी के चुम्बकीय क्षेत्र के क्षैतिज घटक का मान ज्ञात कीजिए।
(b) कुण्डली में धारा की दिशा उलट दी जाती है तथा इसको अपनी ऊर्ध्वाधर अक्ष पर वामावत दिशा में (ऊपर से देखने पर) 90° के कोण पर घुमा दिया जाता है। चुम्बकीय सुई किस दिशा में ठहरेगी? इस स्थान पर दिक्पात शून्य लीजिए।
हल: 
(a) चुम्बकीय सुई पश्चिम से पूर्व की ओर संकेत करती है, इसका अर्थ यह हुआ कि कुण्डली के कारण उत्पन्न चुम्बकीय क्षेत्र BC एवं क्षैतिज घटक H का परिणामी क्षेत्र (resultant field) B पश्चिम से पूर्व की ओर है।
अब दिया है: N = 30; r = 12 cm = 0.12 m; I = 0.35 A 
∴ कुण्डली के कारण उत्पन्न चुम्बकीय क्षेत्र
B_C = \(\frac{\mu_0}{2} \frac{\mathrm{NI}}{r}\)
परिणामी क्षेत्र \(\overrightarrow{\mathrm{WE}}\) दिशा में है, अत: B_C का \(\overrightarrow{\mathrm{SN}}\) दिशा में घटक H के बराबर होगा।

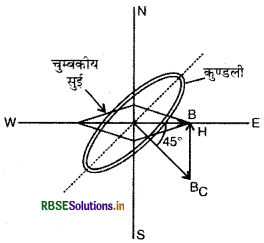
∴ H = B_C cos 45°
या H = B_C x \(\frac{1}{\sqrt{2}}=\frac{\mu_0}{2} \cdot \frac{\mathrm{NI}}{r} \times \frac{1}{\sqrt{2}}\)
या H = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \pi \mathrm{NI}}{r} \times \frac{1}{\sqrt{2}}\)
∴ H = \(10^{-7} \times \frac{2 \times 3.14 \times 30 \times 0.35}{0.12 \times 1.414}\)
= 388.6 x 10^-7
= 0.39 x 10^-4 T = 0.39 G

(b) जब कुण्डली में धारा की दिशा उलट दी जाती है तथा कुण्डली को वामावर्त (anti - clockwise) दिशा में 90° घुमा दिया जाता है तो कुण्डली द्वारा उत्पन्न क्षेत्र B_C की दिशा W - S होगी और B_C तथा H का परिणामी अब \(\overrightarrow{E W}\) दिशा में होगा जिससे सुई की दिशा उलट जायेगी।

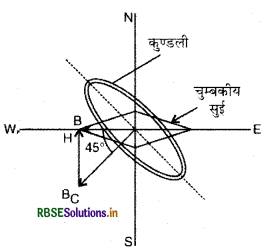
प्रश्न 21. 
एक चुम्बकीय द्विध्रुव दो क्षेत्रों के प्रभाव में है। ये क्षेत्र एक - दूसरे से 60° का कोण बनाते हैं तथा उनमें से एक क्षेत्र का परिमाण 1.2 x 10^-2 T है। यदि द्विथुव स्थायी सन्तुलन (stable equilibrium) में इस क्षेत्र से 15° का कोण बनाये तो दूसरे क्षेत्र का परिमाण क्या होगा?
हल: 
सन्तुलन के लिए चुम्बकीय द्विध्रुव पर नेट बल - आघूर्ण शून्य होना चाहिए, अत: चुम्बकीय क्षेत्रों B1 व B2 द्वारा द्विध्रुव पर आरोपित बल - आघूर्ण बराबर एवं विपरीत (equal and opposite) होने चाहिए अर्थात्
τ₁ = τ₂
या MB₁ sinθ₁ = MB₂ sinθ₂
B₂ = \(\frac{\mathrm{B}_1 \sin \theta_1}{\sin \theta_2}\)

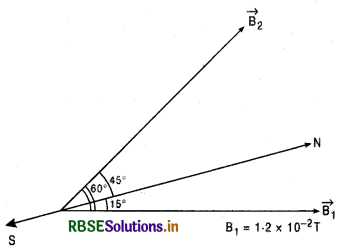
दिया है: B₁ = 1.2 x 10^-2 T; θ₁ = 15°;
θ₂ = (60° - θ₁) = 60 - 15° = 45°
∴ B₂ = \(\frac{1.2 \times 10^{-2} \times \sin 15^{\circ}}{\sin 45^{\circ}}\)
= \(\frac{1.2 \times 10^{-2} \times 0.2588}{0.7071}\)
= 0.439 x 10^-2
= 4.4 x 10^-3 T

प्रश्न 22. 
एक समोर्जी 18 keV वाले इलेक्ट्रॉनों के किरण पुंज पर जो शुरू में क्षैतिज दिशा में गतिमान है, 0.04 G का एक क्षैतिज चुम्बकीय क्षेत्र, जो किरण पुंज की प्रारंभिक दिशा के लंबवत है, लगाया गया है। आकलन कीजिए 30 cm की क्षैतिज दूरी चलने में किरण पुंज कितनी दूरी ऊपर या नीचे विस्थापित होगा? (me = 9.11 x 10^-31 kg, e = 1.60 x 10^-19 C)।
(नोटः इस प्रश्न में ऑकड़े इस प्रकार चुने गए हैं कि उत्तर से आपको यह अनुमान हो, कि TV सेट में इलेक्ट्रॉन गन से पर्दे तक इलेक्ट्रॉन किरण पुंज की गति भू - चुम्बकीय क्षेत्र से किस प्रकार प्रभावित होती है।
हल: दिया है: इलेक्ट्रॉन पुंज की गतिज ऊर्जा

E_K = 18 keV
= 18 x 10³ x 1.6 x 10^-19 J
=18 x 1.6 x 10^-16 J
चुम्बकीय क्षेत्र B = 0.04 G
= 0.04 x 10^-4 T
क्षैतिज दूरी x = 30 cm = 0.30m
∵ \(\mathrm{E}_{\mathrm{K}}=\frac{1}{2} m v^2\)
∴ v = \(\sqrt{\frac{2 \mathrm{E}_{\mathrm{K}}}{m}}\)
∴इलेक्ट्रॉन का संवेग (momentum),
m v = \(m \sqrt{\frac{2 \mathrm{E}_{\mathrm{K}}}{m}}=\sqrt{2 m \mathrm{E}_{\mathrm{K}}}\)
∵ इलेक्ट्रॉन पुंज चुम्बकीय क्षेत्र में क्षेत्र के लम्बवत् प्रवेश करता है, अत: उसका मार्ग वृत्ताकार (circular) होगा जिसकी त्रिज्या
r = \(\frac{m v}{e \mathrm{~B}}=\frac{\sqrt{2 m \mathrm{E}_{\mathrm{K}}}}{e \mathrm{~B}}\)
r = \(\frac{\sqrt{2 \times 9.11 \times 10^{-31} \times 18 \times 1.6 \times 10^{-16}}}{1.6 \times 10^{-19} \times 0.04 \times 10^{-4}}\)
= 11.3 m
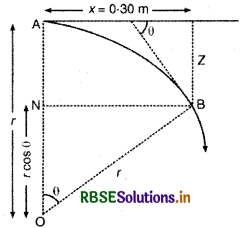
ऊपर या नीचे विक्षेप
Z = AN = r - rcosθ = r (1 - cosθ)
चित्र से, sinθ =\(\frac{x}{r}=\frac{0 \cdot 30}{11 \cdot 3} \)
∵ θ बहुत बेटा है, अतः
sinθ = θ = \(\frac{0 \cdot 30}{11 \cdot 3} \)
∵ cos²θ = 1 - sin² θ = 1 - θ²
क्योंकि sinθ = θ
∴ cosθ = (1 - θ²)^1/2
= \(1-\frac{\theta^2}{2}+\ldots . .,\)
द्विपद प्रमेय से (by Binomial Theorem)
या \(\cos \theta=1-\frac{\theta^2}{2}\)
∴ 1 - cosθ = \(\frac{\theta^2}{2}\)
अतः Z = \(r(1-\cos \theta)=r \cdot \frac{\theta^2}{2}\)
या \(\mathrm{Z}=\frac{11.3}{2}\left(\frac{0.30}{11.3}\right)^2\)
या Z = \(\frac{11.3}{2} \times \frac{0.30 \times 0.30}{11.3 \times 11.3}\)
∴ Z = 0.00398 m
= 3.98 mm ≈ 4 mm

प्रश्न 23. 
अनुचुम्बकीय लवण के एक नमूने में 2.0 x 10²⁴ परमाणु द्विधुव हैं, जिनमें से प्रत्येक का द्विषुव आघूर्ण 1.5 x 10^-23 JT^-1 है। इस नमूने को 0.84 T के एकसमान चुम्बकीय क्षेत्र में रखा गया तथा 4.2 K ताप तक ठण्डा किया गया है। इसमें 15% चुम्बकीय संतृप्तता आ गई। यदि इस नमूने को 0.98 T के चुम्बकीय क्षेत्र में 2.8 K ताप पर रखा हो, तो इसका कुल द्विषुव आघूर्ण कितना होगा? (यह मान सकते हैं कि क्यूरी नियम लागू होता है)
हल: 
प्रत्येक परमाणु द्विध्रुव का चुम्बकीय द्विध्रुव आघूर्ण
= 1.5 x 10^-23 JT^-1 
परमाणु द्विध्रुवों की संख्या N = 2.0 x 10²⁴ 
कुल प्रारम्भिक द्विध्रुव आघूर्ण
\(\begin{aligned} m &=\left(\frac{15}{100} \times 2 \cdot 0 \times 10^{24}\right) \times 1.5 \times 10^{-23} \\ &=4 \cdot 5 \mathrm{JT}^{-1} \end{aligned}\)
क्यूरी के नियम से, \(m \propto \frac{\mathrm{B}}{\mathrm{T}}\)
यदि अन्तिम द्विध्रुव आघूर्ण m' हो, तो
\(\frac{m^{\prime}}{m}=\frac{\mathrm{B}^{\prime}}{\mathrm{B}} \times \frac{\mathrm{T}}{\mathrm{T}^{\prime}}=\left(\frac{\mathrm{B}^{\prime}}{\mathrm{B}}\right) \times\left(\frac{\mathrm{T}}{\mathrm{T}^{\prime}}\right)\)
\(\therefore \quad \mathrm{M}^{\prime}=\left(\frac{\mathrm{B}^{\prime}}{\mathrm{B}}\right) \times\left(\frac{\mathrm{T}}{\mathrm{T}^{\prime}}\right) \times m\)
\(=\left(\frac{0.98}{0.84}\right) \times\left(\frac{4.2}{2.8}\right) \times 4.5\)
= 7.9 JT^-1

प्रश्न 24. 
एक रोलैण्ड रिंग की औसत त्रिज्या 15 cm है तथा इसमें 800 आपेक्षिक चुम्बकशीलता के लौह - चुम्बकीय क्रोड पर 3500 फेरे लिपटे हुए हैं। 1.2 A की चुम्बककारी धारा के कारण इसके क्रोड में कितना चुम्बकीय क्षेत्र (B) होगा?
हल: 
दिया है: µ₁ =  800; r = 15 cm = 0.15 m; N = 3500; I = 1.2 A
चुम्बकीय क्षेत्र 
\(\mathrm{B}=\mu_r \mu_0 \mathrm{NI}=\mu_r \mu_0\left(\frac{\mathrm{N}}{2 \pi r}\right) \mathrm{I}=\frac{\mu_r \mu_0 \mathrm{NI}}{2 \pi r}\)
\(\therefore B=\frac{800 \times 4 \pi \times 10^{-7} \times 3500 \times 1.2}{2 \times \pi \times 0.15}=4.48 \mathrm{~T}\)

प्रश्न 25.
किसी इलेक्ट्रॉन का नैज चक्रणी कोणीय संवेग \(\overrightarrow{\mathbf{S}}\) एवं कक्षीय कोणीय संवेग \(\overrightarrow{\mathbf{S}}\) से सम्बद्ध (associated) चुम्बकीय आघूर्ण क्रमशः \(\vec{\mu}_{\mathbf{S}} \text { व } \overrightarrow{\mu_{\mathbf{L}}}\) हैं। क्वाण्टम सिद्धान्त के आधार पर (और प्रयोगात्मक रूप से पूर्णतः पुष्ट) इनके मान क्रमशः निम्न प्रकार दिये जाते हैं
\(\overrightarrow{\mu_{\mathrm{S}}}=-\left(\frac{e}{m}\right) \overrightarrow{\mathrm{S}}\)एवं \(\overrightarrow{\mu_{\mathrm{L}}}=-\left(\frac{e}{2 m}\right) \overrightarrow{\mathrm{L}}\)
इनमें से कौन - सा व्यंजक चिरसम्मत सिद्धान्तों के आधार पर प्राप्त करने की आशा की जा सकती है? उस चिरसम्मत आधार पर प्राप्त होने वाले व्यंजक को व्युत्पन्न कीजिए।
हल: 
दोनों दिये गये सम्बन्धों में से \(\overrightarrow{\mu_{\mathrm{L}}}=-\left(\frac{e}{2 m}\right) \overrightarrow{\mathrm{L}}\) चिरसम्मत भौतिकी के अनुरूप है। इसे निम्न प्रकार व्युत्पन्न किया जा सकता है-
µ₁ व L की परिभाषाओं के अनुसार,
µ_L = LA, जहाँ I धारा है। 
कक्षा में परिक्रमी इलेक्ट्रॉन के लिए,
तुल्य धारा I = \(\frac{e}{\mathrm{~T}}\)
एवं कक्षा का क्षेत्रफल A = πr²
∴ चुम्बकीय आघूर्ण
\(\mu_{\mathrm{L}}=\left(\frac{e}{\mathrm{~T}}\right) \pi r^2\) ..............(1)
∵ कोणीय संवेग L = mvr
\(\therefore \quad \mathrm{L}=m \cdot\left(\frac{2 \pi r}{\mathrm{~T}}\right) r=\frac{2 \pi m r^2}{\mathrm{~T}}\) ............(2)
समी. (1) को (2) से भाग देने पर,
\(\frac{\mu_{\mathrm{L}}}{\mathrm{L}}=\frac{e}{2 m}\)
∴ \(\mu_{\mathrm{L}}=\left(\frac{e}{2 m}\right) \mathrm{L}\)
चूँकि इलेक्ट्रॉन पर आवेश ऋणात्मक है, \(\overrightarrow{\mu_{\mathrm{L}}} \text { व } \overrightarrow{\mathrm{L}}\) दिशाओं में हैं, अतः सदिश रूप में,
\(\vec{\mu}_{\mathrm{L}}=-\left(\frac{e}{2 m}\right) \overrightarrow{\mathrm{L}}\)
दूसरा परिणाम \(\overrightarrow{\mu_{\mathrm{S}}}=-\left(\frac{e}{m}\right) \overrightarrow{\mathrm{S}}\), क्वाण्टम यान्त्रिकी के अनुसार है तथा चिरसम्मत सिद्धान्तों से व्युत्पन्न नहीं किया जा सकता है।