RBSE Solutions for Class 12 Physics Chapter 4 गतिमान आवेश और चुंबकत्व

Rajasthan Board RBSE Solutions for Class 12 Physics Chapter 4 गतिमान आवेश और चुंबकत्व Textbook Exercise Questions and Answers.

RBSE Class 12 Physics Solutions Chapter 4 गतिमान आवेश और चुंबकत्व

RBSE Class 12 Physics गतिमान आवेश और चुंबकत्व Textbook Questions and Answers

प्रश्न 1. 
तार की एक वृत्ताकार कुण्डली में 100 फेरे (turns) हैं, प्रत्येक की त्रिज्या 8.00 cm है और इसमें 0.40A बारा प्रवाहित हो रही है। कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र का परिमाण क्या है?
हल: 
दिया है: 
फेरों की संख्या n = 100; त्रिज्या r = 8.0 cm = 8.0 x 10^-2m; धारा i = 0.40A; केन्द्र पर B = ?
∵ धारावाही कुण्डली के केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र की तीव्रता
\(\mathrm{B}=\frac{\mu_0}{2} \cdot \frac{n i}{r}=\frac{\mu_0}{4 \pi} \cdot \frac{2 \pi n i}{r}\)
\(\therefore \quad \mathrm{B}=10^{-7} \frac{2 \times 3.14 \times 100 \times 0.40}{8 \times 10^{-2}}\)
= 3.14 x 10^-4 T

प्रश्न 2.  
एक लम्बे सीधे तार (long straight wire) में 35 A विद्युत् थारा प्रवाहित हो रही है। तार से 20 cm दूरी पर स्थित किसी बिन्दु पर चुम्बकीय क्षेत्र का परिमाण क्या है?
हल: 
दिया है:
धारा i = 35 A; तार से बिन्दु की दूरी r = 20 cm = 0.20 m
उत्पन्न चुम्बकीय क्षेत्र B = ? 
∵ लम्बे सीधे तार के कारण उत्पन्न चुम्बकीय क्षेत्र
\(\mathrm{B}=\frac{\mu_0}{2 \pi} \cdot \frac{i}{r}=\frac{\mu_0}{4 \pi} \cdot \frac{2 i}{r}\)
\(\therefore \quad \mathrm{B}=\frac{10^{-7} \times 2 \times 35}{0.2}\)
= 35 x 10^-6
= 3.5  x 10^-5 T

प्रश्न 3. 
क्षैतिज तल में रखे एक लम्बे सीधे तार में 50 A विद्युत् धारा उत्तर से दक्षिण की ओर प्रवाहित हो रही है। तार के पूर्व में 2.5 m दूरी पर स्थित किसी बिन्दु पर उत्पन्न चुम्बकीय क्षेत्र B का परिमाण और उसकी दिशा ज्ञात कीजिए।
हल: 
दिया है: 
तार में धारा I  = 50 A; बिन्दु की तार से दूरी r = 2.5 m (पूर्व में)
उत्पन्न चुम्बकीय क्षेत्र B = ? 
तार के कारण उत्पन्न चुम्बकीय क्षेत्र
B = 2 x 10^-7 \(\frac{\mathrm{I}}{r}\)
= 2 x 10^-7 x \(\frac{50}{2 \cdot 5}\) = 4 x 10^-6 T
सीधे हाथ की हथेली के नियम से चुम्बकीय क्षेत्र की दिशा ऊर्ध्वाधर ऊपर (vertically upwards) की ओर होगी।

प्रश्न 4. 
व्योम में स्थित खिंचे क्षैतिज बिजली के तार (horizontal overhead power line) में 90 A विद्युत् धारा पूर्व से पश्चिम की ओर प्रवाहित हो रही है। तार के 1.5m नीचे विद्युत् धारा के कारण उत्पन्न चुम्बकीय क्षेत्र का परिमाण एवं दिशा क्या है?
हल: 
तार में धारा I = 90 A; तार से बिन्दु की दूरी r = 1.5 m; चुम्बकीय क्षेत्र की तीव्रता B=?
लम्बे धारावाही तार के निकट उत्पन्न चुम्बकीय क्षेत्र
B = 2 x 10^-7 \(\frac{\mathrm{i}}{r}\)
= 2 x 10^-7  x \(\frac{90}{1.5}\) = 12  x 10^-6
∴ B = 1.2 x 10^-5 T
(दायें हाथ की हथेली के नियम से चुम्बकीय क्षेत्र की दिशा क्षैतिज तल में उत्तर से दक्षिण की ओर होगी।)

प्रश्न 5. 
एक तार जिसमें 8A विद्युत् थारा प्रवाहित हो रही है, 0.15 T के एकसमान चुम्बकीय क्षेत्र में, क्षेत्र से 30° का कोण बनाते हुए रखा है। इसकी एकांक लम्बाई पर लगने वाले बल का परिमाण और इसकी दिशा क्या है?
हल: 
दिया है: 
तार में धारा i = 8 A; चुम्बकीय क्षेत्र B = 0.15 T; तार व क्षेत्र के बीच कोण θ = 30°;
तार की लम्बाई l = 1 m 
बल F = ?
∵ F = iBl sinθ
∴ F = 8 x 0.15 x 1 x sinθ
= 8 x 0.15 x \(\frac{1}{2}\) = 0.6 Nm^-1
इस बल की दिशा चुम्बकीय क्षेत्र की दिशा एवं धारा की दिशा दोनों के लम्बवत् फ्लेमिंग के बायें हाथ के नियम से प्राप्त होगी।

प्रश्न 6. 
एक 3.0 cm लम्बा तार जिसमें 10A विद्युत् चारा प्रवाहित हो रही है, एक परिनालिका के भीतर उसकी अक्ष के लम्बवत् रखा है। परिनालिका के भीतर चुम्बकीय क्षेत्र का मान 0.27 T है। तार पर लगने वाला बल क्या है?
हल: 
दिया है: 
तार की लम्बाई l = 3.0 cm = 3.0 x 10^-2 m; धारा i = 10 A; चुम्बकीय क्षेत्र की तीव्रता B = 0.27 T; तार पर बल F = ?
∵ धारावाही परितालिका दण्ड (bar magnet) की भाँति व्यवहार करती है। परिनालिका के भीतर चुम्बकीय क्षेत्र उसकी अक्ष के अनुदिश (along) होगा, अत: चुम्बकीय क्षेत्र तार की लम्बाई के लम्बवत् होगा।
∴ θ = 90°
∵ F = iBl sinθ
∴ F = 10 x 0.27 x 3.0 x 10^-2 x sin 90°
= 2.7 x 3.0 x 10^-2 x 1
= 8.1 x 10^-2 N

प्रश्न 7. 
एक - दूसरे से 4.0 cm की दूरी पर रखे दो लम्बे, समान्तर तारों A एवं B से क्रमश: 8.0 A एवं 5.0 A की विद्युत् धाराएँ एक ही दिशा में प्रवाहित हो रही हैं। तार A के 10 cm खण्ड (section) पर बल का आकलन कीजिए।
हल: 
दिया है: तारों के मध्य दूरी r = 4.0 cm = 4.0 x 10^-2 m; धाराएँ I₁ = 8.0 A एवं I₂ = 5.0 A; लम्बाई l = 10 cm = 0.10 m; F=? 
∵ तार की l लम्बाई पर लगने वाला बल,
F =\(\frac{\mu_0}{2 \pi} \cdot \frac{\mathrm{I}_1 \mathrm{I}_2 \cdot l}{r} \mathrm{~N}\)
\(\begin{aligned} &=\frac{\mu_0}{4 \pi} \times \frac{2 \mathrm{I}_1 \mathrm{I}_2 l}{r} \\ &=2 \times 10^{-7} \frac{\mathrm{I}_1 \mathrm{I}_2 l}{r} \end{aligned}\)
∴ F = 2 x 10^-7 x \(\frac{8 \cdot 0 \times 5 \cdot 0 \times 0.10}{4 \cdot 0 \times 10^{-2}}\)
= 2 x 10^-5 N
(आकर्षणात्मक A के लम्बवत् B की ओर)

प्रश्न 8. 
पास - पास फेरों (closely wound) वाली एक परिनालिका 80 cm लम्बी है और इसमें 5 परतें (layers) हैं जिनमें से प्रत्येक में 400 फेरे हैं। परिनालिका का व्यास 1.8 cm है। यदि इसमें 80A विद्युत् धारा प्रवाहित हो रही है तो परिनालिका के भीतर केन्द्र के पास चुम्बकीय क्षेत्र \(\overrightarrow{\mathbf{B}}\) का परिमाण परिकलित कीजिए।
हल: 
दिया है: 
परिनालिका की लम्बाई l = 0.80 m; त्रिज्या r = 0.9 cm = 0.9 x 10^-2 m; धारा i = 8.0 A; कुल फेरे N = 5 x 400 = 2000
∴ परिनालिका की एकांक लम्बाई में फेरों की संख्या
n = \(\frac{\mathrm{N}}{l}=\frac{2000}{0.8}\) = 2500 m^-1
अतः परितालिका की अक्ष पर उसके केन्द्र के पास उत्पन्न चुम्बकीय क्षेत्र की तीव्रता
B = \(\mu_0 . n i\)
= \(\frac{\mu_0}{4 \pi} \cdot 4 \pi n i\)
= 10^-7 x 4 x 3.14 x 2500 x 8.0
= 3.14 x 8 x 10^-3
= 25.12 x 10^-3
= 2.512 x 10^-2 T
= 2.5 x 10^-2 T

प्रश्न 9. 
एक वर्गाकार कुण्डली (square coil) जिसकी प्रत्येक भुजा 10 cm है; में 20 फेरे हैं और उसमें 12 A विद्युत् धारा प्रवाहित हो रही है। कुण्डली कांचरतः (vertically) लटकी हुई है। इसके तल पर खींचा गया अभिलम्ब 0.80 T के एकसमान चुम्बकीय क्षेत्र की दिशा से 30° का कोण बनाता है। कुण्डली पर लगने वाले बलयुग्म के आघूर्ण का परिमाण क्या है?
हल: 
कुण्डली में फेरों की संख्या N = 20; धारा i = 12 A; कुण्डली की एक भुजा की लम्बाई l = 0.1 m; चुम्बकीय क्षेत्र B = 0.80 T; θ = 30° ; बलयुग्म का आपूर्ण τ = ? 
कुण्डली के तल का क्षेत्रफल
A = l x l = 0.1 x 0.1 = 0.01 x m²
∴ τ = NiAB sin θ
= 20 x 12 x 0.01 x 0.80 x sin 30°
= 20 x12 0.01 x 0.80 x \(\frac{1}{2}\)
= 96 x 10^-2 = 0.96 N m

प्रश्न 10. 
दो चलकुण्डल धारामापी M₁ एवं M₂ के विवरण नीचे दिये गये हैं-
R₁ = 10Ω; N₁ = 30;
A₁ = 3.6 x 10^-3 m²; B₁ = 0.25 T;
R₂ = 14Ω; N₂ = 42;
A₂ = 1.8 x 10^-3 m²; B₂ = 0.50 T (दोनों मीटरों के लिए स्प्रिंग नियतांक समान हैं।) 
(a) M₂ एवं M₁ की धारा - सुनाहिताओं,
(b) M₂ एवं M₁ की वोल्टता - सुग्राहिताओं का अनुपात ज्ञात कीजिए।
हल: 
(a) धारामापी की धारा सुग्राहिता (current sensitivity) = \(\frac{\mathrm{NBA}}{k}\), जहाँ k स्प्रिंग नियतांक है।

क्योंकिका मान दोनों के लिए समान है।

(b) धारामापी की वोल्टता सुग्राहिता (voltage sensitivity) = \(\frac{\mathrm{NBA}}{k \mathrm{R}}\)

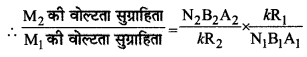
= \(\frac{N_2 B_2 A_2}{N_1 B_1 A_1} \times \frac{R_1}{R_2}\)
= धारा सुग्राहिताओं का अनुपात x \(\frac{\mathrm{R}_1}{\mathrm{R}_2}\)
= 1.4 x \(\frac{10}{14}=\frac{14}{14}\) = 1

प्रश्न 11.
एक प्रकोष्ठ (chamber) में 6.5G (1G = 10^-4 T) का एकसमान चुम्बकीय क्षेत्र बनाये रखा गया है। इस चुम्बकीय क्षेत्र में एक इलेक्ट्रॉन 4.8 x 10^-6 ms^-1 के वेग से क्षेत्र के लम्बवत् भेजा गया है। व्याख्या कीजिए कि इस इलेक्ट्रॉन का पथ वृत्ताकार क्यों होगा? वृत्ताकार कक्षा की त्रिज्या ज्ञात कीजिए।
हल: 
वृत्ताकार पथ की व्याख्या (explanation of circular path): लरिन्ज बल की दिशा आवेश की गति की दिशा एवं चुम्बकीय क्षेत्र की दिशा दोनों के लम्बवत् होती है अर्थात् लॉरेन्ज बल सदैव आवेशित कण की गति के लम्बवत् रहता है, अत: क्षेत्र में लम्बवत् प्रवेश करने पर कण का मार्ग वृत्ताकार (circular) होगा क्योंकि वृत्तीय पथ पर गतिशील कण पर लगने वाला अभिकेन्द्रीय (centripetal) बल सदैव कण के वेग के लम्बवत् रहता है।
पथ की त्रिज्या: दिया है: चुम्बकीय क्षेत्र की तीव्रता B = 6.5 G = 6.5 x 10^-4 T;  इलेक्ट्रॉन का आवेश q = 1.6 x 10^-19 C; वेग v = 4.8 x 10⁶ ms^-1
θ  = 90° ∴ sinθ = 1 
अत: इलेक्ट्रॉन के वृत्तीय पथ की त्रिज्या
r = \(\frac{m v}{q \mathrm{~B}}=\frac{9.1 \times 10^{-31} \times 4.8 \times 10^6}{1.6 \times 10^{-19} \times 6.5 \times 10^{-4}}\)
= 4.2 x 0.2 m
= 4.2 cm

प्रश्न 12. 
प्रश्न 11 में, वृत्ताकार कक्षा में इलेक्ट्रॉन की परिक्रमण आवृत्ति (frequency of revolution) प्राप्त कीजिए। क्या यह उत्तर इलेक्ट्रॉन के वेग पर निर्भर करता है? व्याख्या कीजिए।
हल: 
इलेक्ट्रॉन का वेग v = 4.8 x 10⁶ ms^-1; कक्षा की त्रिज्या r = 4.2 x 10^-2 m; आवेश (q) = e; आवृत्ति v = ?; B = 6.5 x 10^-4 T; m = 9.1 x 10^-31kg
∵  r = \(\frac{m v}{q \mathrm{~B}}\) और आवर्तकाल T = \(\frac{2 \pi r}{v}\)
∴ T = \(\frac{2 \pi}{v} \times \frac{m v}{q \mathrm{~B}}=\frac{2 \pi m}{q \mathrm{~B}}\)
अत: आवृत्ति v = \(\frac{1}{\mathrm{~T}}=\frac{q \mathrm{~B}}{2 \pi m}=\frac{e \mathrm{~B}}{2 \pi m}\)
\(\therefore \quad v=\frac{1.6 \times 10^{-19} \times 6.5 \times 10^{-4}}{2 \times 3.14 \times 9.1 \times 10^{-31}}\)
= 18.18 x 10⁶ Hz
= 18.18 MHz
∵आवृत्ति के सूत्र \(\left(v=\frac{e \mathrm{~B}}{2 \pi m}\right)\) में इलेक्ट्रॉन की चाल v नहीं है, अत: यह उत्तर इलेक्ट्रॉन के वेग पर निर्भर नहीं करेगा।

प्रश्न 13. 
(a) 30 फेरों वाली एक वृत्ताकार कुण्डली जिसकी त्रिज्या 8.0 cm है और जिसमें 6.0 A विधुत् धारा प्रवाहित हो रही है, 1.0 T के एक समान चुम्बकीय क्षेत्र में ऊध्वाधरतः लटकी है। क्षेत्र - रेखाएँ कुण्डली के अभिलम्ब से 60° का कोण बनाती हैं। कुण्डली को घूमने से रोकने के लिए जो प्रति आघूर्ण लगाना चाहिए उसके परिमाण का परिकलन कीजिए (counter torque)।
(b) यदि (a) में बतायी गई वृत्ताकार कुण्डली को उसी क्षेत्रफल की अनियमित आकृति (Irregular shape) की समतलीय कुण्डली से प्रतिस्थापित (replaced) कर दिया जाये(शेष सभी विवरण अपरिवर्तित रखे) तो क्या आपका उत्तर परिवर्तित (change) हो जायेगा?
हल: 
(a) फेरों की संख्या N = 30; त्रिज्या r = 8.0 x 10^-2 m; i= 6.0 A; चुम्बकीय क्षेत्र B = 1.0 T; θ = 60° 
∵ चुम्बकीय क्षेत्र में कुण्डली पर लगने वाले बलयुग्म का आपूर्ण
τ = NiAB sinθ
= 30 x 6.0 x (πr²) x 1.0 sin 60°
= 30 x 6.0 x 3.14 x 8.0 x 10^-2 x 8.0 x 10^-2 x 1.0 x \(\frac{\sqrt{3}}{2}\)
= 3.13 Nm
अत: कुण्डली के घूर्णन को रोकने के लिए आवश्यक प्रति आघूर्ण = 3.13 Nm
(b) सूत्र: τ = NiAB sinθ से स्पष्ट है कि का मान केवल A के मान पर निर्भर करता है, कुण्डली की आकृति पर नहीं, अतः प्रश्न (a) के उत्तर में कोई परिवर्तन नहीं होगा।

प्रश्न 14. 
दो समकेन्द्रिक वृत्ताकार कुण्डलियाँ (cocentric circular coils) X और Y जिनकी त्रिज्याएँ क्रमशः 16 cm एवं 10 cm हैं, उत्तर - दक्षिण दिशा में समान ऊर्ध्वाधर तल में अवस्थित (lie) हैं। कुण्डली x में 20 फेरे हैं और इसमें 16 A विद्युत् धारा प्रवाहित हो रही है; कुण्डली Y में 25 फेरे हैं और इसमें 18 A विद्युत् धारा प्रवाहित हो रही है। पश्चिम की ओर मुख करके खड़ा एक प्रेक्षक (observer) देखता है कि X में धारा प्रवाह वामावर्त (anticlockwise) है। जबकि Y में धारा प्रवाह दक्षिणावर्त (clockwise) है। कुण्डलियों के केन्द्र पर; उनमें प्रवाहित विद्युत् धाराओं के कारण उत्पन्न कुल चुम्बकीय क्षेत्र का परिमाण एवं दिशा ज्ञात कीजिए।

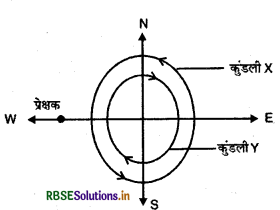
हल: 
दिया है: कुण्डली X के लिए, 
r₁ = 0.16 m; N₁ = 20; i₁ = 16 A 
कुण्डली Y के लिए, 
r₂ = 0.10 m; N₂ = 25; i₂ = 18 A 
कुण्डली X के केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र
\(\mathrm{B}_x=\frac{\mu_0}{2} \cdot \frac{\mathrm{N}_1 i_1}{r_1}=\frac{\mu_0}{4 \pi} \cdot \frac{2 \pi \mathrm{N}_1 i_1}{r_1}\)
\(\therefore \quad \mathrm{B}_x=10^{-7} \times \frac{2 \times \pi \times 20 \times 10}{0.16}\)
= 4π x 10^-4 T (कि X में धारा की दिशा वामवर्त है अत: चुम्बकीय क्षेत्र पूर्व की ओर होगा) 
कुण्डली Y के केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र
\(\mathrm{B}_y=\frac{\mu_0}{2} \cdot \frac{\mathrm{N}_2 i_2}{r_2}=\frac{\mu_0}{4 \pi} \cdot \frac{2 \pi \mathrm{N}_2 i_2}{r_2}\)
\(\therefore \quad B_y=10^{-7} \times \frac{2 \pi \times 25 \times 18}{0.10}\)
= 9π x 10^-4  (कि Y में धारा की दिशा दक्षिणावर्त है अत: चुम्बकीय क्षेत्र पश्चिम की ओर होगा) 
∴ दोनों कुण्डलियों के केन्द्र पर उत्पन्न परिणामी चुम्बकीय क्षेत्र
B = B_y - B_x
= 9π x 10^-4 - 4π x 10^-4
= 5π x 10^-4 T (पश्चिम की ओर)
=  5 x 3.14 x 10^-4
= 15.70 x 10^-4 T
= 15.7 x 10^-3 T
= 1.6 x 10^-3 T (पश्चिम की ओर)

प्रश्न 15.
10 cm लम्बाई और 10^-3 m² अनुप्रस्थ काट के एक क्षेत्र में 100G(1G = 10^-4 T) का एकसमान चुम्बकीय क्षेत्र चाहिए। जिस तार से परिनालिका का निर्माण करना है, उसमें अधिकतम 15 A विद्युत् धारा प्रवाहित हो सकती है और क्रोड (core) पर अधिकतम 1000 फेरे प्रति मीटर लपेटे जा सकते हैं। इस उद्देश्य (required purpose) के लिए परिनालिका के निर्माण का विवरण सुझाइए (appropriate design particulars)। यह मान लीजिए कि क्रोड लौहचुम्बकीय नहीं है।
हल: 
माना परिनालिका की एकांक लम्बाई में फेरों की संख्या n है तथा उसमें प्रवाहित धारा i है। तब उसकी अक्ष पर केन्द्रीय भाग में उत्पन्न चुम्बकीय क्षेत्र
B = µ₀ni ⇒ ni =\( \frac{\mathrm{B}}{\mu_0}\)
∵ B = 100G  = 100 x 10^-4 T
= 10^-2 T नियत है और µ0 भी नियतांक है।
∴ दी गई परिनालिका के लिए ni = नियतांक
∵इस प्रतिबन्ध में दो चर राशियाँ है; अतः हम किसी एक राशि को दी गई सीमाओं के अनुरूप स्वेच्छ मान देकर दूसरी राशि का चुनाव कर सकते हैं। स्पष्ट है कि अभीष्ट परिनालिका के बहुत से भिन्न - भिन्न विवरण सम्भव है।
∵n i \(=\frac{\mathrm{B}}{\mu_0}=\frac{10^{-2}}{4 \pi \times 10^{-7}}\)
या n i= \(\frac{1}{4 \pi} \times 10^5=\frac{1}{4 \times 3 \cdot 14} \times 10^5\)
या ni = 0.0796 x 10⁵ = 7.96 x 10³
∵दिया है कि परिनालिका में अधिकतम 15 A की धारा प्रवाहित हो सकती है, अत:
\(i \leq 15 \mathrm{~A}\)
अतः धारा i का स्वेच्छ (arbitrary) मान 10 A लेने पर,
n = \( \frac{7.96 \times 10^3}{10}\)
= 7.96 x 10² = 796 ≈ 800
हम जानते हैं कि परिनालिका की अक्ष पर उसके केन्द्रीय भाग में चुम्बकीय क्षेत्र लगभग एकसमान होता है, अत: दिया गया स्थान (जिसकी लम्बाई 10 cm एवं अनुप्रस्थ काट का क्षेत्रफल 10^-3 m² है) परिनालिका की अक्ष के अनुदिश तथा केन्द्रीय भाग में होना चाहिए। अत: परिनालिका की लम्बाई लगभग 50 cm से 100 cm के बीच (10 cm से काफी अधिक) होनी चाहिए तथा परिनालिका का अनुप्रस्थ क्षेत्रफल 10^-3 m² से अधिक होना चाहिए।
माना परिनालिका की त्रिज्या r है तब
πr² > 10^-3 ⇒ r² > \(\frac{10^{-3}}{\pi}\) ⇒r² > \(\frac{10^{-3}}{3 \cdot 14}\)
या r² > 3.18 x 10^-4
∴ r > 1.78 x 10^-2 m या r > 1.78 cm
अतः हम परिनालिका की त्रिज्या 2 cm से अधिक (माना 3 cm) ले सकते हैं।
अतः परिनालिका का विवरण निम्न प्रकार है 
लम्बाई l = 50 cm लगभग; फेरों की संख्या N = nl
= 800 तथा त्रिज्या r = 3 cm

प्रश्न 16. 
I धारावाही N फेरों और R त्रिज्या वाली वृत्ताकार कुण्डली के लिए, इसके अक्ष पर केन्द्र से x दूरी पर स्थित किसी बिन्दु पर चुम्बकीय क्षेत्र के लिए निम्न व्यंजक है:
\(\mathbf{B}=\frac{\mu_0 I^2 N}{2\left(x^2+\mathbf{R}^2\right)^{3 / 2}}\)
(a) स्पष्ट कीजिए, इससे कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र के लिए सुपरिचित परिणाम कैसे प्राप्त किया जा सकता है?
(b) बराबर त्रिज्या R एवं फेरों की संख्या N, वाली दो वृत्ताकार कुण्डलियों एक - दूसरे से R दूरी पर एक - दूसरे के समान्तर, अक्ष मिलाकर रखी गई हैं। दोनों में समान विद्युत् धारा एक ही दिशा में प्रवाहित हो रही है। दर्शाइए कि कुण्डलियों के अक्ष के लगभग मध्य - बिन्दु पर क्षेत्र, एक बहुत छोटी दूरी के लिए जो कि R से कम है, एकसमान है और इस क्षेत्र का लगभग मान निम्नलिखित है-
B = 0.70 \(\frac{\mu_0 \mathrm{NI}}{\mathrm{R}}\)
हल: 
(a) दिये गये सूत्र \(\left(\mathrm{B}=\frac{\mu_0 \mathrm{IR}^2 \mathrm{~N}}{2\left(x^2+\mathrm{R}^2\right)^{3 / 2}}\right)\) में x = 0 रखने पर,
\(\begin{aligned} B &=\frac{\mu_0 I^2 N}{2\left(R^2\right)^{3 / 2}} \\ &=\frac{\mu_0 I^2 N}{2 R^3}=\frac{\mu_0}{2} \cdot \frac{N I}{R} \end{aligned}\)
जो कि स्पष्टतः कुण्डली के केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र का सूत्र है, अत: दिये गये सूत्र से कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र ज्ञात करने के लिए x के स्थान पर शून्य रखना होगा।

(b) प्रश्न के अनुसार रखी दो कुण्डलियों के केन्द्रों, C₁ व C₂ को मिलाने वाली रेखा का मध्य - बिन्दु माना C है और इससे अल्प दूरी d पर एक बिन्दु P स्थित है तो प्रथम कुण्डली के केन्द्र C₁ से बिन्दु P की दूरी

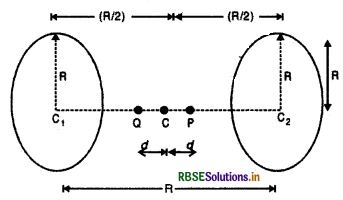
x₁ = \(\left(\frac{\mathrm{R}}{2}+d\right)\)
और दूसरी कुण्डली के केन्द्र से P की दूरी
x₂ = \(\left(\frac{\mathrm{R}}{2}-d\right)\)
∵ दोनों कुण्डलियाँ पूर्णत: एक जैसी है और दोनों में धाराएँ भी समान हैं और एक ही दिशा में है; अतः P पर दोनों के कारण उत्पन्न चुम्बकीय क्षेत्र एक ही दिशा में होंगे। 
∴ P पर परिणामी चुम्बकीय क्षेत्र
B = B₁ + B₂
= \(\frac{\mu_0 \mathrm{NIR}^2}{2\left[\mathrm{R}^2+\left(\frac{\mathrm{R}}{2}+d\right)^2\right]^{3 / 2}}+\frac{\mu_0 \mathrm{NIR}^2}{2\left[\mathrm{R}^2+\left(\frac{\mathrm{R}}{2}-d\right)^2\right]^{3 / 2}}\)

प्रश्न 17.
एक टोरॉइड के (अलौह - चुम्बकीय) (non - ferromagnetic) क्रोड की आन्तरिक (inner) त्रिज्या 25 cm और बाहा (outer) त्रिज्या 26 cm है। इसके ऊपर किसी तार के 3500 फेरे लपेटे गये हैं। यदि तार में प्रवाहित विद्युत् धारा 11 A  हो तो चुम्बकीय क्षेत्र का मान क्या होगा? (i) टोरॉइड के बाहर, (ii) टोरॉइड के क्रोड में (inside the core), (iii) टोरॉइड द्वारा घिरी हुई खाली जगह में (empty space surrounded by the torroid)।
हल: 
दिया है: 
आन्तरिक त्रिज्या r₁ = 0.25 m; बाह्य त्रिज्या r₂ = 0.26 m; फेरों की संख्या N = 3500, धारा i = 11 A
(i) टोरॉइड के बाहर चुम्बकीय क्षेत्र B = 0 
(ii) टोरॉइड की औसत त्रिज्या
r = \(\frac{r_1+r_2}{2}\)
= \(\frac{0.25+0.26}{2}\)
= \(\frac{0.51}{2}\) = 0.255 m
∴ टोरॉइड की क्रोड के अन्दर चुम्बकीय क्षेत्र
B = \(\frac{\mu_0}{2 \pi} \cdot \frac{\mathrm{N} i}{r}=\frac{\mu_0}{4 \pi} \cdot \frac{2 \mathrm{~N} i}{r}\)
∴ B = \(2 \times 10^{-7} \times \frac{3500 \times 11}{0.255}\)
= 3.02 x 10^-2 T
(iii) टोरॉइड द्वारा धेरै गये रिक्त स्थान में चुम्बकीय क्षेत्र
B = 0 

प्रश्न 18. 
निम्नलिखित प्रश्नों के उत्तर दीजिए
(a) किसी प्रकोष्ठ (chamber) में एक ऐसा चुम्बकीय क्षेत्र स्थापित किया गया है जिसका परिमाण तो एक बिन्दु पर बदलता है, पर दिशा निश्चित है (पूर्व से पश्चिम)। इस प्रकोष्ठ में एक आवेशित कण प्रवेश करता है और अविचलित एक सरल रेखा में अचर वेग से चलता रहता है। आप कण के प्रारम्भिक वेग के बारे में क्या कह सकते हैं?
(b) एक आवेशित कण, एक ऐसे शक्तिशाली असमान चुम्बकीय क्षेत्र में प्रवेश करता है जिसका परिमाण एवं दिशा दोनों एक बिन्दु से दूसरे बिन्दु पर बदलते जाते (varying frompoint topoint) हैं; एक जटिल पथ (complicated trajectory) पर चलते हुए इसके बाहर आ जाता है। यदि यह मान लें कि चुम्बकीय क्षेत्र में इसका किसी भी दूसरे कण से कोई संघट्ट नहीं होता तो क्या इसकी अन्तिम चाल, प्रारम्भिक चाल के बराबर होगी?
(c) पश्चिम से पूर्व की ओर चलता हुआ एक इलेक्ट्रॉन एक ऐसे प्रकोष्ठ (chamber) में प्रवेश करता है जिसमें उत्तर से दक्षिण दिशा की ओर एकसमान विद्युत् क्षेत्र है। वह दिशा बताइए जिसमें एकसमान चुम्बकीय क्षेत्र स्थापित किया जाये, ताकि इलेक्ट्रॉन को अपने सरल रेखीय (straight line path) पथ से विचलित (defleet) होने से रोका जा सके। 
उत्तर:
(a) चुम्बकीय क्षेत्र में आवेशित कण पर लगने वाला बल
Fm = qvB sinθ 
यदि θ = 0° या 180° तो sinθ = 0 ∴F = 0
∵प्रकोष्ठ में आवेशित कण अविचलित सरल रेखीय गति करता है, अत: उसकी गति चुम्बकीय क्षेत्र के साथ या तो शून्य या 180° कोण पर होनी चाहिए। स्पष्ट है कि कण का प्रारम्भिक वेग या तो चुम्बकीय क्षेत्र के अनुदिश है अथवा विपरीत दिशा में है।
(b) हाँ, कण की अन्तिम चाल उसकी प्रारम्भिक चाल के बराबर होगी क्योंकि चुम्बकीय बल अर्थात् लरिन्ज बल सदैव कण के वेग के लम्बवत् कार्य करता है, अतः कण के वेग की दिशा तो बदल जायेगी लेकिन उसका परिमाण नहीं बदलेगा अर्थात् चाल नियत रहेगी।
(c) चूँकि विद्युत् एवं चुम्बकीय दोनों क्षेत्रों की उपस्थिति में इलेक्ट्रॉन अविचलित (undeviated) रहकर गति करता है। इसका अर्थ यह हुआ कि उस पर लगने वाले विद्युत् एवं चुम्बकीय बल परिमाण में समान और दिशा में विपरीत होने चाहिए ताकि वे एक-दूसरे को निष्क्रिय कर सकें। चूँकि विद्युत् क्षेत्र की दिशा उत्तर से दक्षिण की ओर है, अत: उसमें इलेक्ट्रॉन पर लगने वाले वैद्युत बल की दिशा उत्तर की ओर (विद्युत् क्षेत्र के विपरीत दिशा में) होगी। स्पष्ट है कि चुम्बकीय बल की दिशा दक्षिण की ओर होनी चाहिए जो फ्लेमिंग के बायें हाथ के नियमानुसार चुम्बकीय क्षेत्र की दिशा ऊध्यधिर नीचे की ओर होनी चाहिए।

प्रश्न 19.
अमित कैथोड (heated cathode) से असर्जित और 2.0 kv के विभवान्तर से त्वरित एक इलेक्ट्रॉन 0.15 T के एक समान चुम्बकीय क्षेत्र में प्रवेश करता है। इलेक्ट्रॉन का गमन - पथ (trajectory) ज्ञात कीजिए यदि चुम्बकीय क्षेत्र (a) प्रारम्भिक वेग के लम्बवत् है, (b) प्रारम्भिक वेग की दिशा से 30° का कोण बनाता है।
हल: 
माना इलेक्ट्रॉन का वेग v है, अत: उसकी गतिज ऊर्जा
E_k = \(\frac{1}{2} m v^2\)
V विभवान्तर से त्वरित होने पर प्राप्त ऊर्जा = V.e जूल
∴ \(\frac{1}{2} m v^2=\mathrm{V} . e \Rightarrow v=\sqrt{\frac{2 \mathrm{~V} . e}{m}}\)
v = \(\sqrt{\frac{2 \times 2 \times 10^3 \times 1 \cdot 6 \times 10^{-19}}{9 \cdot 1 \times 10^{-31}}}\)
= \(\frac{8 \times 10^7}{3.02}=2.65 \times 10^7 \mathrm{~ms}^{-1}\)
(a) ∵ इलेक्ट्रॉन का वेग चुम्बकीय क्षेत्र के लम्बवत् है, अत: इलेक्ट्रॉन का गमन - पथ वृत्ताकार होगा। इस पथ की त्रिज्या

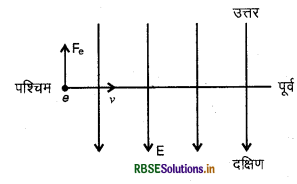
r  =\(\frac{m v}{e \mathrm{~B}}=\frac{9 \cdot 1 \times 10^{-31} \times 2 \cdot 65 \times 10^7}{1 \cdot 6 \times 10^{-19} \times 0 \cdot 15}\)
= 1.00 x 10^-3 m
= 1.0 m
(b) इलेक्ट्रॉन का वेग चुम्बकीय क्षेत्र के साथ 30° का कोण बनाता है, अत: वेग के घटक v cos 30° के कारण इलेक्ट्रॉन का पथ ऋजुरेखीय एवं लम्बवत् घटक v sinθ के कारण वृत्तीय होगा। कुल मिलाकर परिणामी पथ कुण्डलिनीय (helical) होगा। इसकी त्रिज्या
r = \(\frac{m v \sin 30^{\circ}}{e \mathrm{~B}}\)
= \(\left(\frac{m v}{e \mathrm{~B}}\right) \sin 30^{\circ}\)
= 1.0 mm x \(\frac{1}{2}\) = 0.5 mm 

प्रश्न 20. 
प्रश्न 16 में वर्णित हेल्महोल्ट्ज कुण्डलियों (Helmholtz coils) का उपयोग करके किसी लघु क्षेत्र में 0.75 T का एकसमान चुम्बकीय क्षेत्र स्थापित किया है। इसी क्षेत्र में कोई एक समान स्थिर - विद्युत् क्षेत्र कुण्डलियों के उभयनिष्ठ अक्ष के लम्बवत् लगाया जाता है। (एक ही प्रकार के) आवेशित कणों का 15 kV विभवान्तर पर त्वरित एक संकीर्ण किरण पुंज (narrow beam) इस क्षेत्र में दोनों कुण्डलियों के अक्ष तथा स्थिर - विद्युत् क्षेत्र की लम्बवत् दिशा के अनुदिश प्रवेश करता है। यदि यह किरण पुंज 9.0 x 105 Vm^-1; स्थिर - विद्युत् क्षेत्र में अविक्षेपित (undefleeted) रहता है तो यह अनुमान लगाइए कि किरण पुंज में कौन - से कण हैं? यह स्पष्ट कीजिए कि यह उत्तर एकमात्र उत्तर क्यों नहीं है (Why is the answer not unique)?
हल: 
दिया है: 
B = 0. 75 T; E = 9.0 x 10⁵ Vm^-1; V = 15 x 10³ वोल्ट
यदि कण का वेग v, द्रव्यमान m तथा आवेश q है तब कण की गतिज ऊर्जा
\(\frac{1}{2} m v^2=\mathrm{V} \cdot q\)
\(\therefore \quad v=\sqrt{\frac{2 \mathrm{~V} \cdot q}{m}}\)
विद्युत् क्षेत्र के कारण कण पर वैद्युत बल
Fe = qE 
तथा चुम्बकीय बल, Fm = qvB sin 90° = qvB
∵ कण अविचलित रहता है, अत: Fe व Fm के परिमाण समान होंगे और दिशाएँ विपरीत होगी अर्थात्
Fm = Fe
या qvB = qE ⇒ v = \(\frac{E}{B}\)
\(\therefore \quad \sqrt{\frac{2 q \mathrm{~V}}{m}}=\frac{\mathrm{E}}{\mathrm{B}} \Rightarrow \frac{2 q \mathrm{~V}}{m}=\frac{\mathrm{E}^2}{\mathrm{~B}^2}\)
या \(\frac{q}{m}=\frac{\mathrm{E}^2}{2 \mathrm{VB}^2}\)
= \(\frac{\left(9 \cdot 0 \times 10^5\right)^2}{2 \times 15 \times 10^3 \times(0 \cdot 75)^2}\)
= 4.8 x 107 C kg^-1
हम जानते हैं कि प्रोटॉन के लिए \(\frac{q}{m}\) का मान 9.6 x 10⁷ C kg^-1 होता है, जबकि दिये गये कर्णों के लिए \(\frac{q}{m}\) का मान आधा है। इससे स्पष्ट हो जाता है कि इस कण का द्रव्यमान प्रोटॉन के द्रव्यमान का दोगुना होना चाहिए, अत: किरण पुंज में ड्यूटीरियम के आयन उपस्थित हो सकते हैं। परन्तु ड्यूटीरियम ही एकमात्र ऐसा कण नहीं है जिसके लिए \(\frac{q}{m}\) का मान 4.8 x 10⁷ C kg^-1 हो। द्वि - आयनित (doubly ionised) हीलियम परमाणु (अर्थात् α - कण या हीलियम नाभिक He²⁺) के लिए भी \(\frac{q}{m}=\frac{2 e}{2 m}\) तथा त्रि - आयनित (tri - ionised) लीथियम परमाणु (Li³⁺) के लिए \(\frac{q}{m}=\frac{3 e}{3 m}\) का मान यही रहता है।

प्रश्न 21. 
एक सीधी, क्षैतिज चालक छड़ (horizontal conducting rod) जिसकी लम्बाई 0.45 cm एवं द्रव्यमान 60 g है, इसके सिरों पर जुड़े ऊर्ध्वाधर तारों पर लटकी है। तारों से होकर छड़ में 5.0 A विद्युत् धारा प्रवाहित हो रही है।
(a) चालक के लम्बवत् कितना चुम्बकीय क्षेत्र लगाया जाये कि तारों में तनाव शून्य हो जाये?
(b) चुम्बकीय क्षेत्र की दिशा यथावत् रखते हुए यदि विद्युत् धारा की दिशा उत्क्रमित (reversed) कर दी जाये तो तारों में कुल तनाव कितना होगा? (तारों के दव्यमान की उपेक्षा कीजिए) (g = 9.8 ms^-2)
हल: 
दिया है: छड़ की लम्बाई L = 0.45 m; द्रव्यमान m= 0.06 kg; धारा I = 5.0 A
(a) ऊर्ध्वाधर तारों में तनाव (tension) शून्य तब होगा जब धारावाही चालक पर लगने वाला चुम्बकीय बल उसके भार के परिमाण के बराबर एवं विपरीत दिशा में लगे अर्थात्
Fm = Fg
या iBl sin 90°  = mg 
या iBl = mg
\(\therefore \quad \mathrm{B}=\frac{m g}{i l}=\frac{0.06 \times 9.8}{5.0 \times 0.45}=\mathbf{0 . 2 6} \mathbf{T}\)

(b) यदि धारा की दिशा उलट (reverse) दी जाये तो चुम्बकीय बल एवं तार का भार एक ही दिशा में हो जायेंगे, अत: 
तारों में तनाव =mg + i/B sin 90°
= mg + ilB 
= mg + mg (∵iBl = mg) 
= 2 mg 
= 2 x 0.06 x 9.8
=1.176 = 1.18N 

प्रश्न 22. 
एक स्वचालित वाहन (automobile) की बैटरी से इसकी चालन मोटर को जोड़ने वाले तारों में 300 A विद्युत् थारा (अल्पकाल के लिए) (for a short duration) प्रवाहित होती है। तारों के बीच प्रति एकांक लम्बाई पर कितना बल लगता है यदि इनकी लम्बाई 70 cm एवं बीच की दूरी 1.5 cm हो। यह बल आकर्षण बल है या प्रतिकर्षण बल।
हल: 
दिया है:
तारों में धारा i₁ =i₂ = 300 A; तारों के मध्य दूरी r = 1.5 cm = 1.5 x 10^-2 m; तारों की लम्बाई = 70 cm = 0.70m.
∴ तारों के मध्य प्रति एकांक लम्बाई पर लगने वाला बल
F = 2 x 10^-7 \(\frac{\mathrm{I}_1 \mathrm{I}_2}{r} Nm-1\)
= 2 x 10^-7 x \(\frac{300 \times 300}{1.5 \times 10^{-2}}\)
= 1.2 Nm^-1
चूँकि तारों में धारा की दिशाएँ विपरीत हैं अतः यह बल प्रतिकर्षणात्मक (repulsion) होगा।

प्रश्न 23. 
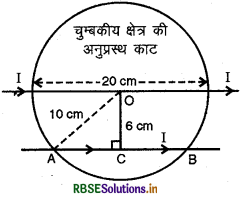
1.5 T का एकसमान चुम्बकीय क्षेत्र, 10.0 cm त्रिज्या के बेलनाकार क्षेत्र (cylinderical region) में विद्यमान है। इसकी दिशा अक्ष के समान्तर पूर्व से पश्चिम की ओर है। एक तार, जिसमें 7.0 A विद्युत् धारा प्रवाहित हो रही है, इस क्षेत्र में होकर उत्तर से दक्षिण की ओर गुजरता है। तार पर लगने वाले बल का परिमाण एवं दिशा क्या है? यदि
(a) तार अक्ष को काटता (intersect) हो,
(b) तार N - S दिशा से घुमाकर (rotate) उत्तर - पूर्व, दक्षिण - पश्चिम दिशा में कर दिया जाये।
(c) N - S दिशा में रखते हुए तार को अक्ष से 6.0 cm नीचे उतार दिया जाये।
हल: 
दिया है: B = 1.5 T; क्षेत्र की त्रिज्या = 10.0 cm; तार में धारा i = 7.0 A
(a) इस दशा में, चुम्बकीय क्षेत्र के अन्दर तार की लम्बाई
l = 2r = 2 x 10 = 20 cm = 0.20 m 
तार का क्षेत्र के साथ कोण θ = 90°

∴तार पर बल
F = iBlsin 90°
=7.0 x 1.5 x 0.20 x 1 = 2.1N 
इस बल की दिशा ऊध्वाधरतः (vertically) नीचे की ओर होगी।
(b) इस स्थिति में तार चुम्बकीय क्षेत्र के साथ 45° का कोण बनायेगा। यदि तार की l1 लम्बाई चुम्बकीय क्षेत्र से होकर गुजरती है तो

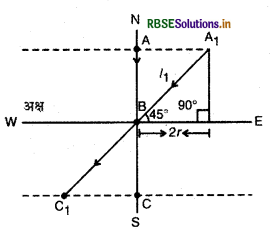
sin 45° = \(\frac{2 r}{l_1}\)
या \(\frac{1}{\sqrt{2}}=\frac{2 r}{l_1}\)
∴ l₁ = \(2r.\sqrt{2}\)
= \(2 \times 10 \sqrt{2}\)
= \(20 \sqrt{2} \mathrm{~cm}\)
= \(20 \sqrt{2} \times 10^{-2} \mathrm{~m}\)
∴तार पर बल
F = il1B. sin 45°
= \(7 \cdot 0 \times 20 \sqrt{2} \times 10^{-2} \times 1 \cdot 5 \times \frac{1}{\sqrt{2}}\)
= 7.0 x 20 x 1.5 x 10^-2
= 2.1 N (कवधिरतः नीचे की ओर) 

(c) इस दशा में तार की AB लम्बाई चुम्बकीय क्षेत्र में क्षेत्र के लम्बवत् होगी। 
चित्र से,
या AC² + OC² = AO² 
या AC² =  AO² -OC²
=(10)² - (6)²
= 100 - 36
= 64 cm², (vertically downward direction),
∴ AC = 8 cm 
अतः AB = 2AC
= 2 x 8
= 16 cm = 16 x 10^-2 m
∴ l2 = 16 x 10^-2 m
अतः F = iBl2 sin 90°
= 7 x 1.5 x 16 x 10^-2 x 1 
= 1.68N (ऊर्ध्वाधरतः नीचे की ओर)

प्रश्न 24. 
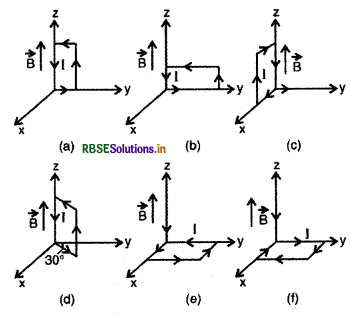
धनात्मक Z - दिशा में 3000 G का एकसमान चुम्बकीय क्षेत्र लगाया गया है। एक आयताकार लूप जिसकी भुजाएँ 10 cm एवं 5 cm हैं और जिसमें 12 A धारा प्रवाहित हो रही है, इस क्षेत्र में रखा है। चित्र में दिखायी गई लूप की विभिन्न स्थितियों में इस पर लगने वाला बलयुग्म आघूर्ण क्या है? हर स्थिति में बल क्या है? स्थायी सन्तुलन (stable equilibrium) वाली स्थिति कौन - सी है?

हल: 
दिया है: B = 3000 G = 3000 x 10^-4 T = 0.3 T; लूप की लम्बाई a = 10 cm = 0.10m
लूप की चौड़ाई b = 5 cm = 0.05 m; धारा I = 12 A
∴ लूप का क्षेत्रफल A = ab
= 0.1 x 0.05 m²
= 0.5 x 10^-2 = 5 x 10^-3 m 
(a), (b), (c), (d) में प्रत्येक दशा में लूप के तल पर खींचा गया अभिलम्ब (normal) चुम्बकीय क्षेत्र के लम्बवत् है, अत: प्रत्येक दशा में लूप पर लगने वाले बलयुग्म का आघूर्ण 
τ = iAB sin 90° = iAB = 12 x 5 x 10^-3 x 0.3 
=1.8 x 10^-2 Nm 
उक्त चारों स्थितियों में लूप पर नेट बल शून्य होगा क्योंकि समान चुम्बकीय क्षेत्र में रखे धारा लूप पर बलयुग्म कार्य करता है, बल नहीं।
∴ (a) τ = 1.8 x 10^-2 Nm; बला शून्य है। 
(b) τ = 1.8 x 10^-2 Nm; बल शून्य है। 
(c) τ = 1.8 x 10^-2 Nm; बल शून्य है।
(d) τ = 1.8 x 10^-2 Nm; बल शून्य है। 
(e) तथा (f), दोनों स्थितियों में लूप के तल पर खींचा गया अभिलम्ब चुम्बकीय क्षेत्र की दिशा में है, अत:
θ = 0
∴ τ = iAB sin0 = 0 
इन दोनों स्थितियों में लुप पर नेट बल एवं बल आपूर्ण दोनों शून्य होंगे, अतः ये दोनों स्थितियाँ ही स्थायी सन्तुलन (stable equilibrium) को व्यक्त करती हैं। नोट - चुम्बकीय आघूर्ण की दिशा के लिए दायें हाथ (right hand thumb rule) का अंगुष्ठ नियम लगाते हैं।

प्रश्न 25. 
एक वृत्ताकार कुण्डली जिसमें 20 फेरे हैं और जिसकी त्रिज्या 10 cm है, एकसमान चुम्बकीय क्षेत्र में रखी है जिसका परिमाण 0.10 T है और जो कुण्डली के तल के लम्बवत् है। यदि कुण्डली में 50 A विद्युत् धारा प्रवाहित हो रही हो तो
(a) कुण्डली पर लगने वाला कुल बलयुग्म - आघूर्ण (torque) क्या है?
(b) कुण्डली पर लगने वाला कुल परिणामी बल क्या है?
(c) चुम्बकीय क्षेत्र के कारण कुण्डली के प्रत्येक इलेक्ट्रॉन पर लगने वाला कुल औसत बल क्या है?
(कुण्डली 10^-5 m² अनुप्रस्थ क्षेत्रफल (cross - seetion) वाले ताँबे के तार से बनी है, और ताँबे में मुक्त इलेक्ट्रॉन घनत्व (free electron density) 1029 m-3 दिया गया है।)
हल: 
दिया है: 
फेरों की संख्या N = 20; धारा I = 5.0 A; त्रिज्या r = 10cm = 0.10 m; चुम्बकीय क्षेत्र B = 0.10 T; मुक्त इलेक्ट्रॉन घनत्व n = 10²⁹ m^-3; तार का अनुप्रस्थ क्षेत्रफल A = 10^-5 m²
(a) ∵ कुण्डली का तल चुम्बकीय क्षेत्र के लम्बवत् है, अत: कुण्डली के तल पर अभिलम्ब व चुम्बकीय क्षेत्र के मध्य कोण θ =0°
∴ τ = NIAB sin 0° = NIA x 0 = 0 शून्य 
(b) कुण्डली पर नेट बल (net force) भी शून्य होगा। 
(c) ∵ चुम्बकीय क्षेत्र में गतिशील आवेश पर बल
F = qvB sinθ 
यहाँ q = e, θ = 90° और v = vd
∴ F = evdB
परन्तु अनुगमन वेग
\(v_d=\frac{i}{\mathrm{Ane}}\)
\(\therefore \quad \mathrm{F}=e \times \frac{i}{\mathrm{An} e} \times \mathrm{B}\)
या \(\mathrm{F}=\frac{i \mathrm{~B}}{\mathrm{~A} n}=\frac{5 \cdot 0 \times 0 \cdot 10}{10^{-5} \times 10^{29}}\)
या = 5 x 10^-25 N
∴ F = 5.0 x 10^-25 N

प्रश्न 26.
एक परिनालिका (solenoid) जो 60 cm लम्बी है, जिसकी त्रिज्या 4.0 cm है और जिसमें 300 फेरों वाली 3 परतें लपेटी गई हैं। इसके भीतर एक 2.0 cm लम्बा, 2.5g दव्यमान का तार इसके (केन्द्र के निकट) अक्ष के लम्बवत् रखा है। तार एवं परिनालिका का अक्ष दोनों क्षैतिज तल में हैं। तार को परिनालिका के समान्तर दो वाही संयाजकों (two leads parallel) द्वारा एक बाह्य बैटरी से जोड़ा गया है जो इसमें 6.0A विद्युत् धारा प्रदान करती है। किस मान की विद्युत् धारा (परिवहन की उचित दिशा के साथ) इस परिनालिका के फेरों में प्रवाहित होने वाले तार का भार संभाल सकेगी? (g=9.8 ms-2)
हल: 
दिया है: परिनालिका की लम्बाई l = 0.6m त्रिज्या r = 4.0 cm = 4.0x10^-2 m; फेरों की संख्या N = 300 x 3 = 900; तार की लम्बाई L = 2.0 cm = 2.0 x 10^-2 m; द्रव्यमान m = 2.5g = 2.5 x 10^-3 kg; धारा I = 6.0 A; g = 9.8 ms^-2
माना परिनालिका (solenoid) में प्रवाहित धारा i है तो उसके अन्दर केन्द्रीय भाग में उत्पन्न चुम्बकीय क्षेत्र
B = \(\mu_0 \cdot \frac{\mathrm{N} i}{l}\) (अक्ष के अनुदिश) 
∵ चुम्बकीय क्षेत्र की दिशा तार की लम्बाई के लम्बवत् है, अत: तार पर लगने वाला बल
F = ILB. sin 90°  = ILB
या = IL x \(\mu_0 \frac{\mathrm{N} i}{l}\)
∵यही बल तार के भार को सन्तुलित करता है, अत:
F = mg
∴ \(\frac{\text { IL. } \mu_0 \cdot \mathrm{N} i}{l}=m g\)
∴ i = \(\frac{m g l}{\mathrm{I} \cdot \mathrm{L} \cdot \mu_0 \cdot \mathrm{N}}\)
= \(\frac{2.5 \times 10^{-3} \times 9.8 \times 0.6}{6.0 \times 2.0 \times 10^{-2} \times 4 \pi \times 10^{-7} \times 900}\)
∴ i = 108 A

प्रश्न 27. 
किसी धारामापी की कुण्डली का प्रतिरोध 12 Ω है। 4 mA की विद्युत् धारा प्रवाहित होने पर यह पूर्ण स्केल विक्षेप (full seale deflection) दर्शाता है। आप इस धारामापीको 0 से 18V परास (range) वाले वोल्टमीटर में कैसे रूपान्तरित (convert) करेंगे?
हल: 
दिया है: G = 12 Ω; I_g = 4 mA = 4 x 10^-3A
0.18 V परास के वोल्टमीटर में बदलने के लिए धारामापी के श्रेणीक्रम में एक उच्च प्रतिरोध R जोड़ना होगा अत:
\(I_g=\frac{V}{R+G} \Rightarrow R+G=\frac{V}{I_g}\)
\(\therefore \quad \mathrm{R}=\frac{\mathrm{V}}{\mathrm{I}_g}-\mathrm{G}=\frac{18}{4 \times 10^{-3}}-12\)
= 4.5 x 10³ -12
= 4500 - 12
∴ R = 4488Ω
अत: धारामापी के श्रेणीक्रम में 4488Ω का प्रतिरोध जोड़ना होगा।

प्रश्न 28. 
किसी धारामापी की कुण्डली का प्रतिरोध 15Ω है और 4 mA की विद्युत् धारा प्रवाहित करने पर यह पूर्ण स्केल विक्षेप (full scale deflection) प्रदर्शित करता है। आप इस धारामापी को 0 से 6 A परास (range) वाले अमीटर में कैसे रूपान्तरित करेंगे? 
हल: 
दिया है: G = 15Ω
I_g = 4.0 mA = 4.0 x 10^-3 A; I = 6.0 A
धारामापी को 0.6 A परास वाले अमीटर में बदलने के लिए इसके समान्तर क्रम में सूक्ष्म प्रतिरोध (low resistance) S का शण्ट जोड़ना होगा, अतः
शण्ट का विभवान्तर = धारामापी का विभवान्तर 
या (I - I_g) x S = I_g x G
\(\therefore \quad \mathrm{S}=\frac{\mathrm{I}_g \times \mathrm{G}}{\left(\mathrm{I}-\mathrm{I}_g\right)}\)
= \(\frac{4 \cdot 0 \times 10^{-3} \times 15}{6.0-4 \cdot 0 \times 10^{-3}}\)
= \(\frac{4 \cdot 0 \times 10^{-3} \times 15}{6 \cdot 0-0 \cdot 004}\)
= \(\frac{4.0 \times 15 \times 10^{-3}}{5.996}=\frac{60}{5.996} \times 10^{-3}\)
≈ \(\frac{60}{6} \times 10^{-3}\) = 10 x 10^-3Ω
∴ S = 10 mΩ
अत: अमीटर बनाने के लिए धारामापी के समान्तर क्रम में 10 mΩ का शण्ट जोड़ना होगा।