RBSE Solutions for Class 12 Physics Chapter 3 विद्युत धारा

Rajasthan Board RBSE Solutions for Class 12 Physics Chapter 3 विद्युत धारा Textbook Exercise Questions and Answers.

RBSE Class 12 Physics Solutions Chapter 3 विद्युत धारा

RBSE Class 12 Physics विद्युत धारा Textbook Questions and Answers

प्रश्न 1. 
किसी कार की संचायक बैटरी (storage battery) का विद्युत् वाहक बल 12 V है। यदि बैटरी का आन्तरिक प्रतिरोध 0.4Ω हो तो बैटरी से ली जाने वाली अधिकतम धारा का मान क्या है?
हल: 
दिया है: 
E = 12V; r = 0.4Ω, I_max = ? 
∵ बैटरी से प्राप्त धारा
I = \(\frac{\mathrm{E}}{\mathrm{R}+r}\)
जहाँ R, बाह्य प्रतिरोध है। सूत्र से स्पष्ट है कि जब बाहा प्रतिरोध (external resistance) R का मान्य शून्य होगा तो I का मान अधिकतम होगा। अत: अधिकतम धारा के लिए
R = 0
∴ I_max = \(\frac{E}{r}=\frac{12}{0 \cdot 4}\) = 30A

प्रश्न 2. 
10V वि. वा. बल वाली बैटरी जिसका आन्तरिक प्रतिरोध (Internal resistance) 3Ω है, किसी प्रतिरोधक से संबोजित (connected) है। यदि परिपथ में धारा का मान 0.5A हो तो प्रतिरोधक का प्रतिरोध क्या है? जब परिपथ बन्द है तो सेल की टर्मिनल वोल्टता क्या होगी?
हल: 
दिया है: 
E = 10V; r = 3Ω; I = 5A; बाड़ा प्रतिरोध R = ? और टर्मिनल वोल्टता V = ? 
∵ सेल से प्राप्त धारा
I = \(\frac{\mathrm{E}}{\mathrm{R}+r} \Rightarrow \mathrm{R}+r=\frac{\mathrm{E}}{\mathrm{I}}\)
∴ R = \(\frac{\mathrm{E}}{\mathrm{I}}-r\)
= \(\frac{10}{0 \cdot 5}-3\) = 20 - 3
∴ R = 17Ω
∵ टर्मिनल वोल्टता
V = E - I.r
= 10 - 0.5 x 3 = 10 - 1.5
या V = 8.5 बोल्ट 

प्रश्न 3. 
(a) 1Ω, 2Ω व 3Ω के तीन प्रतिरोध श्रेणी क्रम में संयोजित हैं। प्रतिरोधकों के संयोजन का कुल प्रतिरोध क्या होगा?
(b) यदि प्रतिरोधकों का संयोजन किसी 12 वोल्ट की बैटरी जिसका आन्तरिक प्रतिरोध नगण्य है, से सम्बद्ध है तो प्रत्येक के सिरों पर वोल्टता पात (potential drop) ज्ञात कीजिए। 
हल: 
(a) दिया है: R₁ = 1Ω, R₂ = 2Ω, R₃ = 3Ω
E = 12V 
माना A तथा B के बीच तुल्य प्रतिरोध R है।
∵ श्रेणीक्रम संयोजन में तुल्य प्रतिरोध
R = R₁ + R₂ + R₃
∴ R = 1 + 2 + 3 = 6Ω

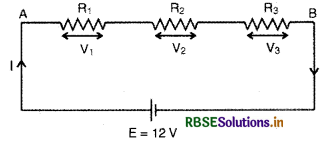
(b) सेल से प्राप्त धारा
I=\(\frac{E}{R}=\frac{12}{6}=2 \mathrm{~A}\)
∴ प्रतिरोधों के सिरों पर वोल्टता ताप
V₁ = IR₁ = 2 x 1 = 2V
V₂ = IR₂ = 2 x 2 = 4V
V₃ = IR₃ = 2 x 3 = 6V

प्रश्न 4. 
(a) 2Ω, 4Ω व 5Ω के तीन प्रतिरोधक पावं क्रम (parallel) में संयोजित हैं। संयोजन का कुल प्रतिरोध क्या होगा?
(b) यदि संयोजन को 20V के वि.वा.बल की बैटरी जिसका आन्तरिक प्रतिरोध नगण्य है, से सम्बद्ध किया जाता है तो प्रत्येक प्रतिरोधक से प्रवाहित होने वाली धारा तथा बैटरी से ली गई कुल धारा (current drawn) का मान ज्ञात कीजिए।
हल: 
(a) दिया है: 
R₁ = 2Ω, R₂ = 4Ω; R₃ = 5Ω
माना A तथा B के मध्य तुल्य प्रतिरोध R है।

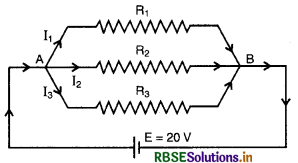
तीनों प्रतिरोध A व B के मध्य समान्तर क्रम में जुड़े हैं, अत: तुल्य प्रतिरोध
\(\frac{1}{\mathrm{R}}=\frac{1}{\mathrm{R}_1}+\frac{1}{\mathrm{R}_2}+\frac{1}{\mathrm{R}_3}\)
या \(\frac{1}{R}=\frac{1}{2}+\frac{1}{4}+\frac{1}{5}\)
या \(\frac{1}{R}=\frac{10+5+4}{20}=\frac{19}{20}\)
∴ R = \(\frac{20}{19} \Omega\)

(b) पूरा समान्तर क्रम संयोजन बैटरी (नगण्य आन्तरिक प्रतिरोध) से जुड़ा है, अत: तीनों के सिरों पर विभवान्तर बैटरी के वि. वा. बल के बराबर होगा।
अत: R₁ से प्रवाहित धारा
I₁ = \(\frac{E}{R_1}=\frac{20}{2}\) = 10A
R₂ से प्रवाहित धारा
I₂ = \(\frac{E}{R_2}=\frac{20}{4}\) = 5A
तथा R₃ से प्रवाहित धारा
I₃ = \(\frac{E}{R_3}=\frac{20}{5}\) = 4A
अत: बैटरी से ली गई कुल धारा
I = I₁ + I₂ + I₃
= 10 + 5 + 4 = 19A

प्रश्न 5.
कमरे केताप(27.0°C) पर किसीतापन - अवयव (heating element) का प्रतिरोध 100Ω है। यदि तापन - अवयव का प्रतिरोध 117Ω हो तो अवयव का तापक्या होगा? प्रतिरोधक के पदार्थ का ताप गुणांक (temperature coefficient)1.70 x 10^-4° C^-1 है। 
हल: 
R₁ = 100Ω, t₁ = 27°C
R₂ = 117Ω,t₂ = ?
α = 1.70 x 10^-4°C^-1
माना t₂ = t₁ + ∆t
तो R₂ = R₁ (1 + α.∆t) = R₁ + R₁α.∆t
या R₁.α.∆t = R₂ - R₁
∴∆t = \(\frac{\mathrm{R}_2-\mathrm{R}_1}{\mathrm{R}_1 \cdot \alpha}\)
= \(\frac{117-100}{100 \times 1 \cdot 70 \times 10^{-4}}=\frac{17 \times 10^4}{170}\)
= 1 x 10³ = 1000°C
∴t₂ = t₁ + ∆t = 27 + 1000 = 1027°C

प्रश्न 6. 
15 मीटर लम्बे एवं 6.0 x 10^-7 m² अनुप्रस्थ काट वाले तार से उपेक्षणीय धारा प्रवाहित की गई है और इसका प्रतिरोध 5.0Ω मापा गया है। प्रायोगिक ताप (temperature of the experiment) पर तार की प्रतिरोधकता क्या होगी?
हल: 
दिया है: 
l = 15 m; A = 6.0 x 10^-7m²; R = 5.0Ω; p = ?
∵ तार का प्रतिरोध
R = \(\rho \cdot \frac{l}{\mathrm{~A}} \Rightarrow \rho=\mathrm{R} \cdot \frac{\mathrm{A}}{l}\)
अतः ρ = \(5 \times \frac{6.0 \times 10^{-7}}{15}\)
= 2 x 10^-7 Ωm

प्रश्न 7. 
सिल्वर के किसी तार का 27.5°C पर प्रतिरोध 2.1Ω और 100°C पर प्रतिरोध 2.7Ω है। सिल्वर की प्रतिरोधकता ताप गुणांक (temperature coefficient of resistance) ज्ञात कीजिए।
हल: 
दिया है: 
t₁ = 27.5°C, R₁ = 2.1Ω,
t₂ = 100°C, R₂ = 2.7Ω,
∵प्रतिरोध बाप गुणांक
α = \(\frac{\mathrm{R}_2-\mathrm{R}_1}{\mathrm{R}_1 t_2-\mathrm{R}_2 t_1}\)
∴ α  =\(\frac{2 \cdot 7-2 \cdot 1}{2.1 \times 100-2 \cdot 7 \times 27 \cdot 5}\)
या α = \(\frac{0 \cdot 6}{210-64 \cdot 25}=\frac{0 \cdot 6}{145 \cdot 75}\)
∴ α = 0.00394°C^-1

प्रश्न 8.
निक्रोम का एक तापन - अवयव 230V की सप्लाई से संयोजित है और 3.2A की प्रारम्भिक धारा लेता है जो कुछ सेकण्ड में 2.8A पर स्थायी (settles) हो जाती है। यदि कमरे का ताप 27.0°C है तो तापन - अवयव का स्थायी ताप क्या होगा? दिये गये ताप - परिसर में निक्रोम के औसत प्रतिरोध का ताप गुणांक 1.70 x 10^-4°C^-1  है।
हल: 
दिया है: V = 230 वोल्ट; i₁ = 3.2A; i₂ = 2.8A
t₁ = 27.0°C, स्थायी ताप t₂ = ?; 
α = 1.70 x 10^-4°C^-1 
प्रारम्भ में (कमरे के ताप पर) प्रतिरोध
R₁ = \(\frac{\mathrm{V}}{i_1}=\frac{230}{3 \cdot 2}\) = 71.87Ω
तप्त अवस्था में (ताप t2 पर) प्रतिरोध
R₂ = \(\frac{\mathrm{V}}{i_2}=\frac{230}{2 \cdot 8}\) = 82.14Ω
माना t₂ - t₁ = ∆t
तो ∆t = \(\frac{\mathrm{R}_2-\mathrm{R}_1}{\alpha \cdot \mathrm{R}_1}\)
या \(\Delta t=\frac{82.14-71.87}{1.70 \times 10^{-4} \times 71.87}\)
= 840°C
∴ t₂ = t₁ + ∆t = 27 + 840
= 867°C

प्रश्न 9.
चित्र में दर्शाए नेटवर्क की प्रत्येक शाखा में प्रवाहित धारा ज्ञात कीजिए।

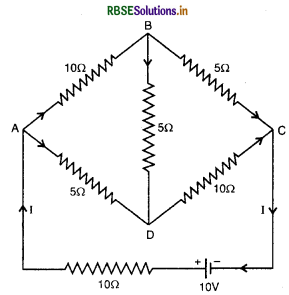
हल: 
नेटवर्क की शाखाओं में धाराओं का विवरण चित्र के अनुसार मान लेते हैं।

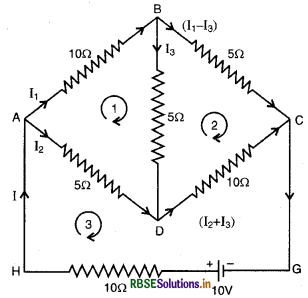
बन्द पाश ABDA के लिए किरौंफ के द्वितीय नियम (ΣE = ΣV = ΣIR) से,
I₁ x 10 + I₃ x 5 - I₂ x 5 = 0
या 10I₁ + 5I₃ - 5I₂ = 0
या 2I₁ - I₂ + I₃ = 0 ..........(i)
बन्द पाश BCD के लिए किरखॉफ के द्वितीय नियम से,
(I₁ - I₃) x 5 - I₃ x 5 - (I₂ +I₃) x 10 = 0
या (I₁ -I₃) - I₃ - (I₂ +I₃) x 2 = 0
या I₁ - I₃ - I₃ - 2I₂ - 2I₃ = 0
या I₁ - 2I₂ - 4I₃ = 0 ..........(ii)
बन्द पाश ADCGHA के लिए,
I₂ x 5 + (I₂ + I₃) x 10 + I x 10 = 10
या 5I₂ + 10I₂ + 10I₃ + 10I = 10
या 15I₂ + 10I₃ + 10I = 10
या 3I₂ + 3I₃ + 2I = 2
बिन्दु A पर सन्धि नियम लगाने पर,
I = I₁ + I₂
∴ 3I₂ + 2I₃ + 2(I₁ + I₂) = 2
या 2I₁ + 5I₂ + 2I₃ = 2 ...............(iii)
समी. (ii) में 2 का गुणा करके समी (i) में से घटाने पर,

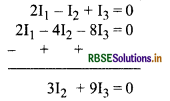
∴ I₂ = -3I₃ .................(iv)
समी. (i) में I₂ का मान रखने पर,
2I₁-(-3I₃) + I₃ = 0 
या 2I₁ + 3I₃ + I₃ = 0 ⇒ 2I₁ + 4I₃ = 0
∴ I₁ = -2I₃ ..................(v)
अब समी. (iii) में I₁ व I₂ के मान समौ. (v) व (iv) से रखने पर,
2 (-2I₃) + 5 (-3I₃) + 2I₃ = 2
या -4I₃ -15I₃ + 2I₃ = 2
या -17I₃ = 2
∴ \(I_3=-\frac{2}{17} \mathrm{~A}\)
∴ समी. (iv) से, \(\mathrm{I}_2=-3\left(-\frac{2}{17}\right)=\frac{6}{17} \mathrm{~A}\)
समी. (v) से, \(I_1=-2\left(-\frac{2}{17}\right)=+\frac{4}{17} \mathrm{~A}\)
∴ I = I₁ + I₂ \(=\frac{4}{17}+\frac{6}{17}=\frac{10}{17} \mathrm{~A}\)
∴ नेटवर्क की भुजा 
AB में धारा = I₁ = \(\frac{4}{17}A\); BD में धारा I₃ = \(-\frac{2}{17}A\)
AD में धारा = I₂ = \(\frac{6}{17}A\)
BC में धारा = I₁ - I₃ = \(\frac{4}{17}-\left(\frac{-2}{17}\right)=\frac{6}{17}A\)
DC में धारा = I₂ + I₃  =\(\frac{6}{17}-\frac{2}{17}=\frac{4}{17}A\)
मुख्य धारा I = I₁ + I₂ = \(\frac{4}{17}+\frac{6}{17}=\frac{10}{17}A\)

प्रश्न 10. 
(a) किसी मीटर सेतु में जब प्रतिरोधक S = 12.5Ω हो तो सन्तुलन बिन्दु (balance point), सिरे A से 39.5 cm की लम्बाई पर प्राप्त होता है। प्रतिरोध R का मान ज्ञात कीजिए। व्हीटस्टोन सेतु या मीटर सेतु में प्रतिरोधको के संयोजन के लिए मोटी कॉपर की पत्तियाँ (thick copper strips) क्यों प्रयोग में लाते हैं?
(b) R तथा S को अन्तर्बदल करने पर उपर्युक्त सेतु का सन्तुलन बिन्दु ज्ञात कीजिए।
(c) यदि सेतु के सन्तुलन की अवस्था में धारामापी और सेल का अन्तर्बदल (interchanged) कर दिया जाये तब क्या धारामापी कोई घारा दर्शाएगा?
हल: 
(a) दिया है:
S = 12.5Ω; l = 39.5 cm; R = ?
∵ सन्तुलित सेतु के लिए,
\(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{\mathrm{R}}{\mathrm{S}}\)  या \(\frac{l}{(100-l)}=\frac{\mathrm{R}}{\mathrm{S}}\)
∴ R = \(\frac{l}{(100-l)} \times \mathrm{S}=\frac{39 \cdot 5 \times 12 \cdot 5}{(160-39 \cdot 5)}\)
= \(\frac{39 \cdot 5 \times 12 \cdot 5}{60 \cdot 5}\) = 8.2Ω
सेतुओं में प्रतिरोधकों के संयोजन के लिए मोटी कॉपर की पत्तियों का उनके प्रतिरोध को न्यूनतम रखने के लिए प्रयोग किया जाता है क्योंकि सूत्र की स्थापना में इनके प्रतिरोध को नगण्य मान लेते हैं।
(b) R व S को परस्पर बदलने पर,
\(\frac{l}{(100-l)}=\frac{\mathrm{S}}{\mathrm{R}}=\Rightarrow \mathrm{R} l=100 \mathrm{~S}-l \mathrm{~S}\)
या Rl + Sl = 100S
या l (R + S) = 100 S
∴ l = \(\frac{100 \mathrm{~S}}{(\mathrm{R}+\mathrm{S})}\)
= \(\frac{100 \times 12 \cdot 5}{8 \cdot 2+12 \cdot 8}=\frac{1250}{21}\)
= 59.52 cm
या l ≈ 59.5 cm

(c) नहीं, सन्तुलन अवस्था में धारामापी एवं सेल को अन्तर्बदल करने पर सन्तुलन बना रहेगा और फलस्वरूप धारामापी से होकर कोई धारा नहीं बहेगी।

प्रश्न 11. 
8v वि. वा. बल की एक संचायक बैटरी (storage battery) जिसका आन्तरिक प्रतिरोध 0.5Ω है, को श्रेणीक्रम में 15.5Ω के प्रतिरोधक का उपयोग करके 120V के D.C. स्रोत द्वारा चार्ज किया जाता है। चार्ज होते समय बैटरी की टर्मिनल वोल्टता क्या है? चार्जकारी परिपथ (charging circuit) में प्रतिरोधक को श्रेणीक्रम में सम्बद्ध करने का क्या उद्देश्य है?
हल: 
दिया है: बैटरी का वि. वा. बल E = 8V; आन्तरिक प्रतिरोध r = 0.5Ω; आवेशन स्रोत का वि. वा. बल E_ext = 120V: बाह्य प्रतिरोध R = 15.5Ω चार्ज होते समय: टर्मिनल वोल्टता V = ? चार्जिग धारा
I = \(\frac{\mathrm{E}_{\mathrm{ext}}-\mathrm{E}}{\mathrm{R}+r}=\frac{(120-8) \mathrm{V}}{(15 \cdot 5+0 \cdot 5)}=\frac{112}{16}=7 \mathrm{~A}\)
∴ चार्ज होते समय टर्मिनल वोल्टता
V = E + Ir = 8 + 7 x 0.5 = 8 + 3.5 = 11.5V
बाह्य प्रतिरोध जोड़ने का उद्देश्य चार्जिंग धारा को कम रखना है क्योंकि उच्च धारा से चार्ज होते समय बैटरी क्षतिग्रस्त हो सकती है।

प्रश्न 12. 
किसी विभवमापी व्यवस्था में, 1.25 V वि. वा. बल से एक सेल का सन्तुलन बिन्दु तार के 35.0 cm लम्बाई पर प्राप्त होता है। यदि इस सेल को किसी अन्य सेल द्वारा प्रतिस्थापित (replaced) कर दिया जाए तो सन्तुलन बिन्दु 63.0 cm पर स्थानान्तरित (shifts) हो जाता है। दूसरे सेल का वि. वा. बल क्या है? 
हल: 
दिया है: E₁ = 1.25 V; l₁ = 35.0 cm;
l₂ = 63.0 cm; E₂ = ?
∵ \(\frac{\mathrm{E}_1}{\mathrm{E}_2}=\frac{l_1}{l_2} \Rightarrow \mathrm{E}_2=\frac{\mathrm{E}_1 l_2}{l_1}\)
∴ E₂ = \(\frac{1.25 \times 63.0}{35}\) = 2.25 V

प्रश्न 13. 
किसी ताँबे के चालक में मुक्त इलेक्ट्रॉनों का संख्या घनत्व (number density) 8.5 x 10²⁸m^-3 आकलित किया गया है। 3m लम्बे तार के एक सिरे से दूसरे सिरे तक अपवाह करने में इलेक्ट्रॉन कितना समय लेता है? तारकी अनुप्रस्थ काट 2.0 x 10^-6m² हैऔर इसमें 3.0A धारा प्रवाहित हो रही है।
हल: 
दिया है: n = 8.5  x 10²⁸ m^-3; l = 3m; A = 2.0 x 10^-6m²; i = 3.0 A
∴इलेक्ट्रॉनों का अनुगमन वेग
vd = \(\frac{i}{\text { A.ne }}\)
= \(\frac{3.0}{2.0 \times 10^{-6} \times 8.5 \times 10^{28} \times 1.6 \times 10^{-19}}\)
= \(\frac{3 \times 10^{-3}}{2 \cdot 0 \times 8 \cdot 5 \times 1 \cdot 6}\)
= 0.11 x 10^-3 ms^-1
∴ इलेक्ट्रॉन को चालक के एक सिरे से दूसरे सिरे तक अनुगमन में लगा समय
t =\( \frac{l}{v_d}=\frac{3.0}{0.11 \times 10^{-3}}\)
= 27.3 x 10³ s = 2.73 x 10⁴ s

प्रश्न 14.
पृथ्वी के पृष्ठ पर ऋणात्मक पृष्ठ आवेश घनत्व (negative surface charge density) 10^-9Cm^-2 है। वायु मण्डल के ऊपरी भाग और पृथ्वी के पृष्ठ के बीच 400 kV विभवान्तर (नीचे के वायुमण्डल की कम चालकता के कारण) के परिणामतः समूची पृथ्वी पर केवल 1800A की धारा है। यदि वायुमण्डलीय विद्युत् क्षेत्र बनाये रखने हेतु कोई प्रक्रिया (mechanism) न हो तो पृथ्वी के पृष्ठ को उदासीन करने हेतु (लगभग) कितना समय लगेगा? (व्यावहारिक रूप में यह कभी नहीं होता है क्योंकि विद्युत् आवेशों की पुनः पूर्ति की एक प्रक्रिया है, यथा पृथ्वी के विभिन्न भागों में लगातार तड़ित झंझा एवं तड़ित (lightning) का होना।) (पृथ्वी की त्रिज्या = 6.37 x 10⁶ m)
हल: 
पृथ्वी की त्रिज्या Re = 6.37x10⁶ m; आवेश का पृष्ठ घनत्व σ = 10^-9 Cm^-2
वायुमण्डल से पृथ्वी पर धारा i = 1800A 
पृथ्वी के निरावेशन में लगा समय t = ? 
पृथ्वी सतह पर कुल आवेश q = σ.A = σ.4πR_e²
∴निरावेशन में लगा समय
∴ t = \(\frac{q}{i}=\frac{\sigma \cdot 4 \pi \mathrm{R}_e^2}{i}\)
t = \(\frac{10^{-9} \times 4 \times 3.14 \times 6.37 \times 6.37 \times 10^{12}}{1800}\)
= \(\frac{4 \times 3.14 \times 6.37 \times 6.37 \times 10}{18}\)
= 28.31 x 10 s = 283.1 s

प्रश्न 15 
(a) छ: लेड एसिड संचायक सेलों (lead acid storage battery) को जिनमें प्रत्येक का विद्युत् वाहक बल 2V तथा आन्तरिक प्रतिरोध 0.015Ω है, के संयोजन से एक बैटरी बनायी जाती है। इस बैटरी का उपयोग 8.5Ω प्रतिरोधक जो इसके साथ श्रेणीक्रम में सम्बद्ध है, में धारा की आपूर्ति के लिए किया जाता है। बैटरी से कितनी धारा ली गई है एवं इसकी टर्मिनल वोल्टता क्या है?
(b) एक लम्बे समय तक उपयोग (after long use) में लाये गये संचायक सेल का विद्युत् वाहक बल 1.9V और विशाल आन्तरिक प्रतिरोध 380Ω है। सेल से कितनी अधिकतम धारा ली जा सकती है? क्या सेल से प्राप्त यह थारा किसी कार की प्रवर्तक मोटर (starting motor) को स्टार्ट करने में सक्षम होगी?
हल: 
(a) यहाँ E = 2.0V; r = 0.015Ω; सेलों की संख्या n = 6; बाह्य प्रतिरोध R = 8.5Ω
∵ सभी सेले श्रेणीबद्ध हैं, अतः संयोजन का वि. वा. बल = nE = 6 x 2.0 = 12V
बैटरी का कुल आन्तरिक प्रतिरोध = 6r = 6 x 0.015 = 0.09Ω
अतः परिपथ का कुल प्रतिरोध = R + nr = 8.5 + 0.09 = 8.59 Ω
 ∴ बैटरी से प्राप्त धारा

=\(\frac{12}{8 \cdot 59}\)= 1.397A
या I = 1.4A
बैटरी की टर्मिनल वोल्टता
V = E - Ir = IR
= 1.4 x 8.5 = 11.9 वोल्ट

(b) यहाँ E = 1.9V; r = 380Ω
अतः बाह्य प्रतिरोध को नगण्य मानते हुए सेल से प्राप्त अधिकतम धारा
I_max = \(\frac{\mathrm{E}}{r}=\frac{1 \cdot 9}{380}=\mathbf{0} \cdot \mathbf{0 0 5} \mathbf{A}\)
कार स्टार्ट करने वाली मोटर को कार्य करने के लिए काफी अधिक धारा लगभग 100A कुछ सेकण्ड के लिए चाहिए होती है। स्पष्ट है कि इस सेल का उपयोग कार स्टार्ट करने के लिए नहीं किया जा सकता है।

प्रश्न 16. 
दो समान लम्बाई की तारों में एक ऐलुमिनियम का और दूसरा कॉपर का बना है। इनके प्रतिरोध समान हैं। दोनों तारों में से कौन - सा हल्का (lighter) है? अतः समझाइए कि ऊपर से जाने वाली बिजली केबिलों में ऐलुमिनियम के तारों को क्यों पसन्द किया जाता है? (ρ_Al = 2.63 x 10^-8 Ωm; ρ_Cu = 1.72 x 10^-8 Ωm; Al का आपेक्षिक घनत्व = 2.7 और Cu का आपेक्षिक घनत्व (relative density) = 8.9)
हल: 
ऐलुमिनियम तार के लिए,
R₁ = R; l₁ = l; आपेक्षिक घनत्व d₁ = 2.7 
ताँबे के तार के लिए,
R₂ = R; l₂ = l; d₂ = 8.9 
यदि ऐलुमिनियम व ताँबे के तारों के अनुप्रस्थ परिच्छेद क्रमश: A₁ व A₂ हो तो
R₁ = \(\rho_1 \frac{l_1}{\mathrm{~A}_1}=\frac{2.63 \times 10^{-8} \times l}{\mathrm{~A}_1}\)
और ऐलुमिनियम तार का द्रव्यमान
m₁ = A₁l₁d₁ = A₁l x 2.7 x 10³ 
इसी प्रकार ताँबे के तार के लिए
R₂ = \(\rho_2 \frac{l_2}{\mathrm{~A}_2}=\frac{1.72 \times 10^{-8} \times l}{\mathrm{~A}_2}\)
और द्रव्यमान m₂ = A₂l₂d₂ =A₂l x 8.9 x 10³ 
दिया है: R₁ = R₂
∴ \(\frac{2 \cdot 63 \times 10^{-8} \times l}{A_1}=\frac{1.72 \times 10^{-8} \times l}{A_2}\)
∴ \(\frac{A_2}{A_1}=\frac{1.72}{2 \cdot 63}\)
= \(\frac{m_2}{m_1}=\frac{\mathrm{A}_2 l \times 8.9 \times 10^3}{\mathrm{~A}_1 l \times 2.7 \times 10^3}\)
= \(\frac{8.9}{2.7} \times \frac{A_2}{A_1}=\frac{8.9}{2.7} \times \frac{1.72}{2.63}\)
= 2.1557
अब \(\frac{m_2}{m_1}=\mathbf{2} \cdot \mathbf{1 6}\)
स्पष्ट है कि ताँबे का तार ऐलुमिनियम के तार से 2.16 गुना अधिक भारी है।
चूँकि समान लम्बाई एवं समान प्रतिरोध के लिए ऐलुमिनियम का तार ताँबे के तार से हल्का है। इसीलिए ऊपर से जाने वाली बिजली की केबिलों में ऐलुमिनियम के तारों को पसन्द किया जाता है। ताँबे के तारों से युक्त केबिल अपने भार से ही नीचे की ओर झूलने लगेगी और खम्भे भी अधिक मजबूत बनाने होंगे।

प्रश्न 17. 
मिश्रधातु (alloy) मैंगनिन के बने प्रतिरोध पर लिए गये निम्नलिखित प्रेक्षणों से आप क्या निष्कर्ष निकाल सकते हैं?

हल: 
सारणी के प्रत्येक प्रेक्षण से, \(\frac{\mathrm{V}}{\mathrm{I}} \approx 19.7 \Omega\)
इससे स्पष्ट है कि मैंगनिन का प्रतिरोधक लगभग पूरे वोल्टेज परिसर में औम के नियम का पालन करता है; अर्थात् मैंगनिन की प्रतिरोधकता पर ताप का बहुत कम प्रभाव पड़ता है।

प्रश्न 18. 
निम्नलिखित प्रश्नों के उत्तर दीजिए-
(a) किसी असमान अनुप्रस्थ काट वाले धात्विक चालक से एकसमान धारा प्रवाहित होती है। निम्नलिखित में से चालक में कौन - सी राशि अचर रहती है - धारा, धारा धनत्व, विद्युत् क्षेत्र, अपवाह चाल।
(b) क्या सभी परिपथीय अवयवों के लिए ओम का नियम सार्वत्रिक रूप से लागू होता है? यदि नहीं, तो उन अवयवों के उदाहरण दीजिए जो ओम के नियम का पालन नहीं करते हैं।
(e) किसी निम्न वोल्टता संभरण (low voltage supply) जिससे उच्च धारा देनी होती है, का आन्तरिक प्रतिरोध बहुत कम होना चाहिए, क्यों?
(d) किसी उच्च विभव (H.T.) संभरण, मान लीजिए 6 kV का आन्तरिक प्रतिरोध अत्यधिक होना चाहिए, क्यों?
उत्तर:
(a) असमान अनुप्रस्थ परिच्छेद वाले चालक से होकर केवल धारा नियत रहती है, शेष राशियाँ चालक के अनुप्रस्थ परिच्छेद क्षेत्रफल के व्युत्क्रमानुपाती होती हैं।
(b) नहीं, ओम का नियम सभी परिपथीय अवयवों पर लागू नहीं होता। निर्वात नलिकाएँ (डायोड वाल्व, ट्रायोड वाल्व), अर्द्धचालक युक्तियाँ (संधि डायोड, ट्रांजिस्टर) इसी प्रकार की युक्तियाँ हैं।
(c) किसी संभरण से प्राप्त महत्तम धारा
I_max = \(\frac{\mathrm{E}}{r}\)
∵ वि. वा. बल कम है; अतः पर्याप्त धारा प्राप्त करने के लिए आन्तरिक प्रतिरोध का मान कम होना आवश्यक है। इसके अतिरिक्त आन्तरिक प्रतिरोध के अधिक होने से सेल द्वारा दी गई ऊर्जा का अधिकांश भाग सेल के अन्दर ही व्यय हो जाता है।
(d) यदि आन्तरिक प्रतिरोध बहुत कम है तो किसी कारणवश लघुपथित होने की दशा में संभरण से अति उच्च धारा प्रवाहित होगी और संभरण के क्षतिग्रस्त होने की सम्भावना उत्पन्न हो जायेगी।

प्रश्न 19. 
सही विकल्प छाँटिए-
(a) धातुओं की मिश्र धातुओं की प्रतिरोधकता प्रायः उनकी अवयव धातुओं की अपेक्षा (अधिक/कम) होती है।
(b) आमतौर पर मिश्र धातुओं के प्रतिरोध का ताप गुणांक, शुद्ध धातुओं के प्रतिरोध के ताप गुणांक से बहुत (कम/अधिक) होता है।
(c) मिश्रधातु मैंगनिन की प्रतिरोधकता ताप में वृद्धि के साथ लगभग (स्वतन्त्र है/ तेजी से बढ़ती है)।
(d) किसी प्रारूपी विद्युत्रोधी (उदाहरणार्थ, अम्बर) की प्रतिरोधकता किसी धातु की प्रतिरोधकता की तुलना में (10²²/10²³) कोटि के गुणक (by a facter of the order) से बड़ी होती है।
उत्तर:
(a) अधिक
(b) कम
(c) स्वतन्त्र है
(d) 10²²।

प्रश्न 20. 
(a) आपको R प्रतिरोध वाले n प्रतिरोधक दिये गये हैं।
(i) अधिकतम 
(ii) न्यूनतम प्रभावी प्रतिरोध प्राप्त करने के लिए आप इन्हें किस प्रकार संयोजित करेंगे? अधिकतम और न्यूनतम प्रतिरोधों का अनुपात क्या होगा?
(b) यदि 1Ω, 2Ω, 3Ω के तीन प्रतिरोध दिये गये हों तो उनको आप किस प्रकार संयोजित करेंगे कि प्राप्त तुल्य प्रतिरोध (i) \(\left(\frac{11}{3}\right) \Omega\), (ii) \(\left(\frac{11}{5}\right) \Omega\), (iii) \(6 \Omega\), (iv) \(\left(\frac{6}{11}\right) \Omega\) हो ?
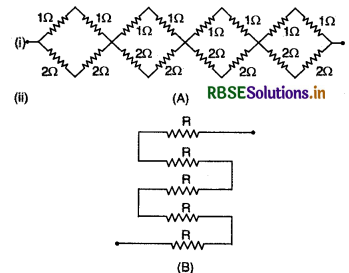
(c) चित्र में दिखाए गए नेटवकों का तुल्य प्रतिरोध ज्ञात कीजिए।

हल: 
(a) (i) अधिकतम प्रतिरोध प्राप्त करने के लिए दिये गये प्रतिरोधों को श्रेणीक्रम में जोड़ना होगा।
R_max = R + R + .................. + R (n तक)
R_max = nR 
(ii) न्यूनतम प्रतिरोध प्राप्त करने के लिए सभी प्रतिरोधों को समान्तर क्रम में जोड़ना होगा, अत:
\(\begin{aligned} \frac{1}{\mathrm{R}_{\text {mim }}} &=\frac{1}{\mathrm{R}}+\frac{1}{\mathrm{R}}+\ldots \ldots+\frac{1}{\mathrm{R}}(n \text { तक }) \\ &=\frac{n}{\mathrm{R}} \end{aligned}\)
∴ \(\mathrm{R}_{\min }=\frac{\mathrm{R}}{n}\)
∴ \(\frac{\mathrm{R}_{\max }}{\mathrm{R}_{\min }}=\frac{n R}{R / n}=\frac{n^2}{1}=n^2: 1\)

(b) (i) R₁ = 1Ω; R₂ = 2Ω; R₃ = 3Ω
परिणामी प्रतिरोध \(\frac{11}{3} \Omega\) प्राप्त करने के लिए R₁, R₂ को समान्तर क्रम में एवं R₃ को उसके श्रेणीक्रम में जोड़ना होगा।

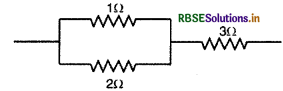
पुष्टि - 1Ω व 2Ω के समान्तर क्रम संयोजन का प्रतिरोध R' हो तो
\(\frac{1}{\mathrm{R}^{\prime}}=\frac{1}{1}+\frac{1}{2}=\frac{3}{2}\)
⇒ \(\mathrm{R}^{\prime}=\frac{2}{3} \Omega\)
∴ R_eq = R' + 3
= \(\frac{2}{3}+3=\frac{11}{3} \Omega\)
(ii) \(\frac{11}{5} \Omega\) का प्रतिरोध प्राप्त करने के लिए R₂ व R₃ को समान्तर क्रम में एवं R₁ को उसके श्रेणीक्रम में जोड़ना होगा।

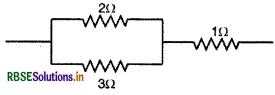
पुष्टि - R₂ व R₃ के समान्तर क्रम संयोजन का प्रतिरोध यदि R हो तो
\(\frac{1}{\mathrm{R}^{\prime}}=\frac{1}{2}+\frac{1}{3}=\frac{5}{6}\)
⇒ R' = \(\frac{6}{5} \Omega\)
∴ R_eq = R' + R₁
= \(\frac{6}{5}+1=\frac{11}{5} \Omega\)
(iii) 6Ω का प्रतिरोध प्राप्त करने के लिए तीनों को श्रेणीक्रम में जोड़ना होगा।
∴ R_eq = R₁ + R₂ + R₃
= 1 + 2 + 3
= 6Ω
(iv) का प्रतिरोध प्राप्त करने के लिए तीनों को पार्श्व क्रम में जोड़ना होगा।
∴ \(\frac{1}{\mathrm{R}_{\mathrm{eq}}}=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}\)
=\(\frac{6+3+2}{6}=\frac{11}{6}\)
∴ R_eq =  \(\frac{6}{11} \Omega\)

(c) (i) चित्र (A) में प्रदर्शित नेटवर्क में एक जैसे चार पाश श्रेणीबद्ध हैं। प्रत्येक पाश में 1-1 तथा 2-2Ω के प्रतिरोध श्रेणीक्रम में जुड़े हैं और ये दोनों संयोजन समान्तर क्रम में जुड़े हैं, अत: एक पाश का तुल्य प्रतिरोध यदि R, हो तो अतः पूरे नेटवर्क का तुल्य प्रतिरोध
\(\frac{1}{\mathrm{R}_1}=\frac{1}{1+1}+\frac{1}{2+2}=\frac{1}{2}+\frac{1}{4}=\frac{3}{4}\)
∴ \(\mathrm{R}_1=\frac{4}{3} \Omega\)
अतः पूरे नेटवर्क का तुल्य प्रतिरोध
R_eq = R₁ + R₁ + R₁ + R₁
= 4R₁ = 4 x \(\frac{4}{3}=\frac{16}{3} \Omega\)
(ii) चित्र (B) में प्रदर्शित नेटवर्क में RΩ के पाँच प्रतिरोध श्रेणीक्रम में जुड़े हैं, अतः तुल्य प्रतिरोध
R_eq = R + R + R + R + R = 5R

प्रश्न 21. 
किसी 0.5Ω आन्तरिक प्रतिरोध वाले 12V के एक संभरण (supply) से चित्र में दर्शाए गये अनन्त नेटवर्क द्वारा ली गई धारा का मान ज्ञात कीजिए। प्रत्येक प्रतिरोध का मान 1Ω है।

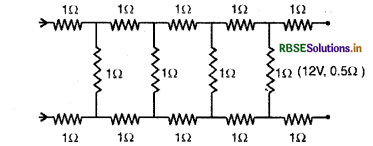
हल: 
माना पूरे नेटवर्क का प्रतिरोध R है। यदि इस नेटवर्क में तीन प्रतिरोध (प्रत्येक 1Ω)अग्र चित्र के अनुसार जोड़ दिये जायें तो भी नेटवर्क के प्रतिरोध में कोई परिवर्तन

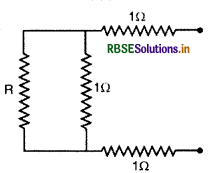
नहीं होगा क्योंकि यह नेटवर्क अनन्त है। इस नेटवर्क में R व 1Ω के प्रतिरोध पार्श्व क्रम में जुड़े हैं, अतः तुल्य प्रतिरोध (R')
\(\frac{1}{R^{\prime}}=\frac{1}{R}+\frac{1}{1}=\frac{(1+R)}{R}\)
⇒ R'  = \(\frac{R}{(1+R)}\)
∴ R_eq = 1Ω + R' + 1Ω
=1+\(\frac{\mathrm{R}}{(1+\mathrm{R})}+1=2+\frac{\mathrm{R}}{(1+\mathrm{R})}\)
∵ R_eq = R
∴ R = 2+\(\frac{R}{(1+R)}\)
∴\(\mathrm{R}=\frac{2+2 \mathrm{R}+\mathrm{R}}{(1+\mathrm{R})}=\frac{2+3 \mathrm{R}}{(1+\mathrm{R})}\)
या R (1 + R) = 2 + 3R
या R + R² = 2 + 3R
या R² + R - 3R -2 = 0
या R² - 2R - 2 = 0
\(\begin{aligned} \therefore \quad \mathrm{R} &=\frac{2 \pm \sqrt{(-2)^2-4 \times 1(-2)}}{2} \\ &=\frac{2 \pm \sqrt{4+8}}{2}=\frac{2 \pm 2 \sqrt{3}}{2} \end{aligned}\)
या R = 1 \(\pm \sqrt{3}\)
∵ R का मान ऋणात्मक नहीं हो सकता है, अतः
R = 1 + \(\sqrt{3}\)
= 1 + 1.732
= 2.732Ω = 2.73Ω
∴ संभरण से ली गई धारा
i = \(\frac{\mathrm{E}}{\mathrm{R}+r}=\frac{12 \mathrm{~V}}{2 \cdot 73+0 \cdot 5}\)
= \(\frac{12}{3 \cdot 23}\) = 3.71A

प्रश्न 22.
चित्र में एक विभवमापी दर्शाया गया है जिसमें एक 2.0V और आन्तरिक प्रतिरोध 0.40Ω का कोई सेल, विभवमापी के प्रतिरोधक तार AB पर वोल्टता पात (voltage drop) बनाए रखता है। कोई मानक सेल (standard cell) जो 1.02V का अचर वि. वा. बल बनाए रखता है। (कुछ mA की बहुत सामान्य धाराओं के लिए) तार की 67.3 cm लम्बाई पर सन्तुलन बिन्दु देता है। मानक सेल से अति न्यून धारा (very low current) लेना सुनिश्चित (ensure) करने के लिए इसके साथ परिपथ में 600 kΩ श्रेणी का एक अति उच्च प्रतिरोध सम्बद्ध किया जाता है, जिसे सन्तुलन बिन्दु प्राप्त होने के निकट लघुपचित (shorted) कर दिया जाता है। इसके बाद मानक सेल को किसी अज्ञात वि. वा. बल E के सेल से प्रतिस्थापित (replaced) कर दिया जाता है जिससे सन्तुलन बिन्दु तार की 82.3 cm लम्बाई पर प्राप्त होता है।

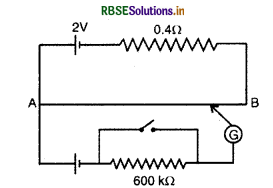
(a)E का मान क्या है? 
(b) 600 kΩ के उच्च प्रतिरोध का क्या प्रयोजन (purpose) है?
(c) क्या इस उच्च प्रतिरोध से सन्तुलन बिन्दु प्रभावित होता है?
(d) उपर्युक्त स्थिति में यदि विभवमापी के परिचालक सेल (driver cell) का वि. वा. बल 2.0V के स्थान पर 1.0V हो तो क्या यह विधि फिर भी सफल होगी?
(e) क्या यह परिपथ कुछ mv की कोटि के अत्यल्प (extremely small) विधुत् वाहक बलों (जैसे कि किसी प्रारूपी ताप विद्युत् युग्म का विद्युत वाहक बल (such as the typical emf of a thermo - couple) के निर्धारण में सफल होगी? यदि नहीं, तो आप इसमें किस प्रकार संशोधन (modify) करेंगे? 
हल: 
(a) दिया है: 
E₁ = 1.02V;  l₁ = 67.3 cm
E₂ = E = ? ; l₂ = 82.3 cm
∵ \(\frac{\mathrm{E}_2}{\mathrm{E}_1}=\frac{l_2}{l_1}\)
∴ \(\frac{\mathrm{E}}{\mathrm{E}_1}=\frac{l_2}{l_1} \Rightarrow \frac{\mathrm{E}}{1 \cdot 02}=\frac{82.3}{67 \cdot 3}\)
या E=\(\frac{82 \cdot 3 \times 1 \cdot 02}{67 \cdot 3}\)
1.247 = 1.25 बोल्ट 
(b) जब सम्पर्क बिन्दु सन्तुलन बिन्दु से काफी दूर होता है तो ε पारामापी से कम धारा गुजारने के उद्देश्य से 600 kΩ का उच्च प्रतिरोध प्रयोग किया जाता है।
(c) नहीं, क्योंकि शून्य विक्षेप बिन्दु के समीप पहुँचने पर इस प्रतिरोध को लघुपथित कर दिया जाता है।
(d) नहीं, यदि परिचालक सेल का वि. वा. बल मापे जाने वाले वि. वा. बल से कम है तो अविक्षेप स्थिति नहीं मिलेगी।
(e) अत्यल्प वि. वा. बल मापन के लिए परिपथ कार्य नहीं करेगा क्योंकि इसके लिए अविक्षेप बिन्दु A के निकट आयेगा, अत: अत्यल्प वि. वा. बल नापने के लिए विभवमापी तार AB की विभव प्रवणता घटानी होगी और इसके लिए उसमें प्रवाहित धारा कम करनी होगी। धारा कम करने के लिए परिचालक सेल के परिपथ में उच्च प्रतिरोध जोड़ना पड़ेगा।

प्रश्न 23. 
चित्र में किसी 1.5V के सेल का आन्तरिक प्रतिरोध मापने के लिए एक 2.0V का विभवमापी दर्शाया गया है। खुले परिपथ (open circuit) में सेल का सन्तुलन बिन्दु 76.3 cm पर मिलता है। सेल के बाहा परिपथ में 9.5Ω प्रतिरोध का एक प्रतिरोधक संयोजित करने पर सन्तुलन बिन्दु विभवमापी के तार की 64.8 cm लम्बाई पर पहुंच जाता है। सेल के आन्तरिक प्रतिरोध का मान ज्ञात कीजिए। हल: 
सेल का आन्तरिक प्रतिरोध

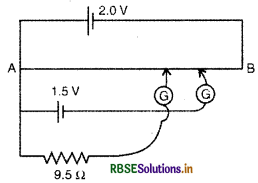
r=\(\left(\frac{\mathrm{E}-\mathrm{V}}{\mathrm{V}}\right) \mathrm{R}=\left(\frac{l_1-l_2}{l_2}\right) \mathrm{R}\)
यहाँ l₁ = 76.3 cm; l₂ = 64.8 cm, R = 9.5Ω
\(\begin{aligned} \therefore \quad r &=\left(\frac{76 \cdot 3-64 \cdot 8}{64 \cdot 8}\right) \times 9 \cdot 5 \\ &=\frac{11 \cdot 5 \times 9 \cdot 5}{64 \cdot 8} \\ &=\mathbf{1} \cdot 7 \Omega \end{aligned}\)