RBSE Solutions for Class 12 Physics Chapter 2 स्थिर वैद्युत विभव तथा धारिता

Rajasthan Board RBSE Solutions for Class 12 Physics Chapter 2 स्थिर वैद्युत विभव तथा धारिता Textbook Exercise Questions and Answers.

RBSE Class 12 Physics Solutions Chapter 2 स्थिर वैद्युत विभव तथा धारिता

RBSE Class 12 Physics स्थिर वैद्युत विभव तथा धारिता Textbook Questions and Answers

प्रश्न 1.
5 x 10^-8 तथा -3x10^-8 C के दो आवेश 16 cm पर स्थित हैं। दोनों आवेशों को मिलाने वाली रेखा के किस बिन्दु पर विद्युत् विभव शून्य होगा? अनन्त पर विभव शून्य मान लीजिए।
हल: 
प्रथम स्थिति में - जब शून्य विभव का बिन्दु दोनों आवेशों के मध्य हो - माना q₁ व q₂ आवेश क्रमशः बिन्दुओं A व B पर स्थित हैं।

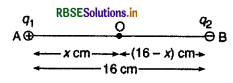
q₁ = +5 x 10^-8 C और q₂ = -3 x 10^-8 C
यदि शून्य विभव वाला बिन्दु P पहले आवेश से x cm की दूरी पर है तो
  

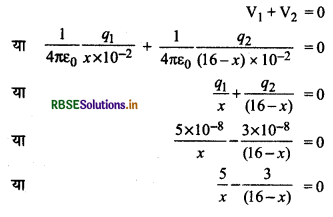
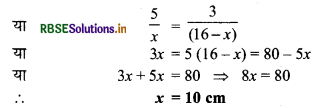
∴ x = 10 cm
द्वितीय स्थिति में-यदि बिन्दु Pबिन्दुओं A व B के मध्य न हो-इस स्थिति में भी प्रथम आवेश से P की दूरी xcm ली गई है, अत: P पर

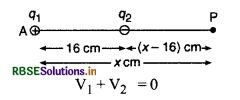
प्रश्न 2.
10 cm भुजा वाले एक सम - घद्भुज (regular hexagon) के प्रत्येक शीर्ष पर 5µC का आवेश है। षद्भुज के केन्द्र पर विभव परिकलित कीजिए।
हल: 
षट्भुज की ज्यामितीय (geometrical) संरचना से स्पष्ट हो जाता है कि सम - षट्भुज के केन्द्र O से प्रत्येक शौर्ष की दूरी षट्भुज को भुजा के बराबर होती है।

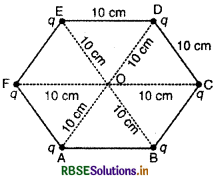
अत: OA = OB = OC = OD = OE = OF = 10 cm = 0.1 m
∴ केन्द्र O पर विभव
V_O = V_A + V_B + V_C + V_D + V_E + V_F = 6V_A क्योंकि आवेश एवं दूरी समान होने के कारण
V_A = V_B = V_C = V_D = V_E = V_F
∴ V_O = 6 x \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{\mathrm{OA}}\)
= 6 x 9 x 10⁹ x \(\frac{5 \times 10^{-6}}{0 \cdot 1}\)
= 27 x 10⁵ 
या V_O = 2.7 x 10⁶ वोल्ट

प्रश्न 3.
6 cm की दूरी पर अवस्थित दो बिन्दुओं A व B पर दो आवेश 2µC तथा -2µC रखे हैं।
(a) निकाय के समविभव (equipotential) पृष्ठ की पहचान कीजिए।
(b) इस पृष्ठ के प्रत्येक बिन्दु पर विद्युत्-क्षेत्र की दिशा क्या होगी?
उत्तर:
(a) चूँकि दोनों आवेश समान परिमाण के परन्तु विपरीत प्रकृति के हैं, अत: समविभव पृष्ठ दोनों आवेशों को मिलाने वाली रेखा AB के लम्बवत् होगा और उसके मध्य - बिन्दु से जायेगा।

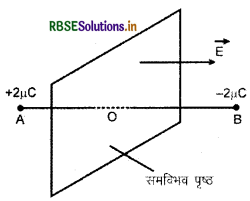
(b) विद्युत् क्षेत्र की दिशा समविभव पृष्ठ के लम्बवत् धनावेश से ऋणावेश की ओर (AB दिशा में) होगी।

प्रश्न 4.
12 cm त्रिज्या वाले एक गोलीय चालक के पृष्ठ पर 1.6 x 10^-7 C पर आवेश एक समान रूप से वितरित है।
(a) गोले के अन्दर 
(b) गोले के ठीक बाहर
(c) गोले के केन्द्र से 18 cm पर अवस्थित (situated) किसी बिन्दु पर विद्युत् - क्षेत्र क्या होगा?
हल: 
(a) गोलाकार चालक के पृष्ठ पर जितना विभव होता है, उतना ही गोले के अन्दर प्रत्येक बिन्दु पर होता है, अत: किन्हीं दो बिन्दुओं के मध्य विभवान्तर ∆V = 0 
∴ विद्युत् क्षेत्र E = \(-\frac{\Delta V}{\Delta x}=0\)

(b) गोले के पृष्ठ के ठीक बाहर स्थित बिन्दु पर विद्युत् क्षेत्र (R = 12 cm = 0.12 m)
E =\( \begin{aligned} &\frac{1}{4 \pi \varepsilon_0} \frac{q}{\mathrm{R}^2} \\ &9 \times 10^9 \times \frac{1.6 \times 10^{-7}}{0.12 \times 0.12} \\ &\frac{9 \times 16}{12 \times 12} \times 10^5=1 \times 10^5 \mathrm{NC}^{-1} \end{aligned}\)

(c) गोले के केन्द्र से r = 18 cm = 0.18 m दूरी पर
E =\( \frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2}\)
= 9 x 10⁹ x \(\frac{1.6 \times 10^{-7}}{0.18 \times 0.18}\)
= \(\frac{9 \times 16}{18 \times 18} \times 10^5\)
= 0.444 x 10⁵
= 4.44 x 10⁴ NC^-1

प्रश्न 5. 
एक समान्तर पट्टिका संधारित्र, जिसकी पट्टिकाओं (plates) के बीच वायु है की धारिता 8 pF (1pF = 10^-12F) है। यदि पट्टिकाओं के बीच की दूरी को आधा कर दिया जाये और इनके बीच के स्थान में 6 परावैद्युतांक (dielectric constant) का एक पदार्थ भर दिया जाये, तो इसकी धारिता क्या होगी?
हल:
दिया है, वायु संधारित्र की धारिता
C₀ = 8pF = 8 x 10^-12 F, परावैद्युतांक K = 6
और संधारित्र को प्लेटों के मध्य दूरी = d/2
∴ C₀ = \(\frac{\mathrm{A} \varepsilon_0}{d}\)  और C = \(\frac{\mathrm{KA} \varepsilon_0}{d/2}\)
या C = 2K \(\frac{\mathrm{A} \varepsilon_0}{d}\) = 2KC₀
= 2 x 6 x 8 x 10^-12 F
= 96 x 10^-12 F = 96 pF

प्रश्न 6.
9 pF धारिता वाले तीन संधारित्रों को श्रेणी क्रम में जोड़ा गया है।
(a) संयोजन की कुल बारिता क्या है?
(b) यदि संयोजन को 120V के संभरण (supply) से जोड़ दिया जाये तो प्रत्येक संधारित्र का विभवान्तर क्या होगा?
हल: 
(a) संयोजन की धारिता

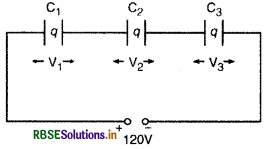
\(\begin{aligned} \frac{1}{C} &=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3} \\ &=\frac{1}{9}+\frac{1}{9}+\frac{1}{9}=\frac{3}{9}=\frac{1}{3} \end{aligned}\)
∴ C = 3 pF
या c = 3 x 10^-12 F

(b) संयोजन पर संचित आवेश
q = CV = 3 x 10^-12 x 120
= 360 x 10^-12 C
यही आवेश तीनों संधारित्रों पर संचित (stored) होगा। अतः प्रत्येक संधारित्र का विभवान्तर भी समान होगा क्योंकि तीनों की धारिता समान है।
∴ V₁ = V₂ = V₃ = \(\begin{aligned} &\frac{q}{C_1} \\ &\frac{360 \times 10^{-12}}{9 \times 10^{-12}}=\mathbf{4 0} \mathrm{V} \end{aligned}\)

प्रश्न 7.
2 pF, 3 pF एवं 4 pF धारिता वाले तीन संधारित्र पार्श्व क्रम (समान्तर क्रम) में जोड़े गए है।
(a) संयोजन की कुल चारिता क्या है?
(b) यदि संयोजन को 100v के संभरण (supply) से जोड़ दें तो प्रत्येक संधारित्र पर आवेश ज्ञात कीजिए। 
हल: 
(a) संबोजन की कुल धारिता
C = C₁ + C₂ + C₃
= 2 + 3 + 4
∴ C = 9 pF

(b) तीनों संधारित्र चित्रानुसार समान्तर क्रम में (in parallel) हैं अत: तीनों का विभवान्तर V = 100 वोल्ट होगा।

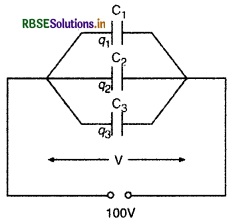
∴ q₁ = C₁V = 2 x 10^-12 x 100
= 200 x 10^-12
= 2.0 x 10^-10 C
इसी प्रकार, q₂ = C₂V = 3 x 10^-12 x 100
= 300 x 10^-12
= 3 x 10^-10 C
और q₃ = C₃V = 4 x 10^-12 x 100
= 400 x 10^-12
= 4 x 10^-10 C

प्रश्न 8.
पट्टिकाओं के बीच वायु वाले समान्तर पट्टिका संधारित्र की प्रत्येक पट्टिका का क्षेत्रफल 6 x 10^-3 m² तथा उनके बीच की दूरी 3 mm है। संधारित्र की बारिता को परिकलित कीजिए। यदि इस संधारित्र को 100V के संभरण (supply) से जोड़ दिया जाए तो संधारित्र की प्रत्येक पट्टिका पर कितना आवेश होगा?
हल: 
दिया है-
A = 6 x 10^-3 m²,
d = 3 mm = 3 x 10^-3 m
V = 100 वोल्ट 
धारिता C₀ = ? और आवेश q = ?
∵ C₀ = \(\frac{\mathrm{A} \varepsilon_0}{d}=\frac{6 \times 10^{-3} \times 8 \cdot 854 \times 10^{-12}}{3 \times 10^{-3}}\)
∴ C₀ = 17.7 x 10^-12 F
= 17.7 pF ≈ 18 pF
संधारित्र पर संचित आवेश q = C₀V
∴ q = 1.8 x 10^-11 x100
= 1.8 x 10^-9 C
∴ एक पट्टिका पर आवेश = +1.8 x 10^-9 C
और दूसरी पट्टिका पर आवेश = -1.8 x 10^-9 C

प्रश्न 9.
प्रश्न 8 में दिये गये संधारित्र की पट्टिकाओं के बीच यदि 3 mm मोटी अभ्रक की एक सीट (परावैधुतांक = 6) रख दी जाती है तो स्पष्ट कीजिए कि क्या होगा जब-
(a) विभव (वोल्टेज) संभरण जुड़ा ही रहेगा? 
(b) संभरण को हटा लिया जायेगा? 
हल: 
दिया है-
A = 6 x 10^-3 m²,
d = 3 mm = 3 x 10^-3 m
V = 100 वोल्ट 
धारिता C₀ = ? और आवेश q = ?
∵ C₀ = \(\frac{\mathrm{A} \varepsilon_0}{d}=\frac{6 \times 10^{-3} \times 8 \cdot 854 \times 10^{-12}}{3 \times 10^{-3}}\)
∴ C₀ = 17.7 x 10^-12 F
= 17.7 pF ≈ 18 pF
संधारित्र पर संचित आवेश q = C₀V
∴ q = 1.8 x 10^-11 x100
= 1.8 x 10^-9 C
∴ एक पट्टिका पर आवेश = +1.8 x 10^-9 C
और दूसरी पट्टिका पर आवेश = -1.8 x 10^-9 C
V = 100 वोल्ट
q = 18 x 10^-10 C, C₀ ≈ 18 pF
माध्यम का परावैद्युतांक K = 6 
परावैद्युत की मोटाई t = d = 33 mm = 3 x 10^-3 m 
अत: परावैद्युत प्लेटों के मध्य के स्थान को पूर्णतः भर देगा। 
∴ नवीन धारिता C = K C₀ = 6 x 18 = 10⁸ pF

(a) चूँकि संधारित्र विभव संभरण से जुड़ा हुआ है अत: संधारित्र का विभवान्तर संभरण के विभवान्तर (100V) के बराबर ही रहेगा।
∴ संधारित्र का नया आवेश
q = CV = 108 x 10^-12 x 100
= 108 x 10^-10 = 1.08 x 10^-8 C
अतः इस स्थिति में,
C = 108 pF, V = 100 वोल्ट, q = 1.08 x 10-8 C

(b) विभव संभरण को हटा लेने पर आवेश वही रहेगा अर्थात्
q = 1.8 x 10-9 C
∴ नया विधवान्तर V' \(\begin{aligned} &=\frac{q}{C}=\frac{1.8 \times 10^{-9}}{108 \times 10^{-12}} \\ &=\frac{1800}{108}=\frac{50}{3}=16.6 \mathrm{~V} \end{aligned}\)
∴ इस स्थिति में,
C = 108 pF, V = \(\frac{50}{3}\) = 16.6 वोल्ट, q = 1.8  x 10^-9 C

प्रश्न 10.
12 pF का एक संधारित्र 50 V की बैटरी से जुड़ा है। संधारित्र में कितनी स्थिर - विद्युत् ऊर्जा संचित होगी?
हल: 
दिया है-
धारिता C = 12 pF = 12 x 10^-12 F, विभवान्तर V = 50 वोल्ट 
∴ संधारित्र की ऊर्जा, 
U= \(\frac{1}{2}\) CV² = \(\frac{1}{2}\) x 12 x 10^-12 x 50 x 50
= 1.5x10^-8 J

प्रश्न 11. 
200 V संभरण से एक 600 pF के संधारित्र को आवेशित किया जाता है। फिर इसको संभरण (supply) से वियोजित (disconnected) कर देते हैं तथा एक अन्य 600 pF वाले अनावेशित (uncharged) संधारित्र से जोड़ देते हैं। इस प्रक्रिया में कितनी ऊर्जा का ह्रास होता है?
हल: 
ऊर्जा का रास,
∆U = \(\frac{\mathrm{C}_1 \mathrm{C}_2}{2\left(\mathrm{C}_1+\mathrm{C}_2\right)}\left(\mathrm{V}_1 \sim \mathrm{V}_2\right)^2\)
प्रश्न से, C₁ = 600 pF = 600 x 10^-12 F
= 6 x 10^-10 F
V₁ = 200V
C₂ = 600 pF = 600 x 10^-12 F
= 6 x 10^-10 F
V₂ = 0
∴ ∆U = \(\begin{aligned} &\frac{6 \times 10^{-10} \times 6 \times 10^{-10}}{2\left(6 \times 10^{-10}+6 \times 10^{-10}\right)}(200 \sim 0)^2 \\ &\frac{6 \times 10^{-10} \times 6 \times 10^{-10} \times 200 \times 200}{2 \times 2 \times 6 \times 10^{-10}} \end{aligned}\)
= 6 x 10^-6 J

प्रश्न 12.
मूलबिन्दु पर एक 8 mC का आवेश अवस्थित (located) है। -2 x 10^-9 C के एक छोटे से आवेश को बिन्दु P.(0,0, 3 cm) से बिन्दु R (0, 6 cm,9 cm) से होकर, बिन्दु Q (0,4 cm, 0) तक ले जाने में किया गया कार्य परिकलित (calculate) कीजिए।

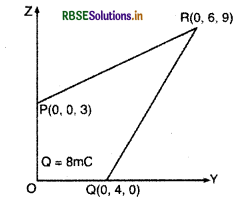
हल: 
मूलबिन्दु O पर मौजूद आवेश,
Q = 8 mC = 8 x 10^-3 C
मूलबिन्दु से बिन्दु P की दूरी, rP = 3 cm = 0.03 m
मूलबिन्दु से बिन्दु Q की दूरी, rQ = 4 cm = 0.04 m

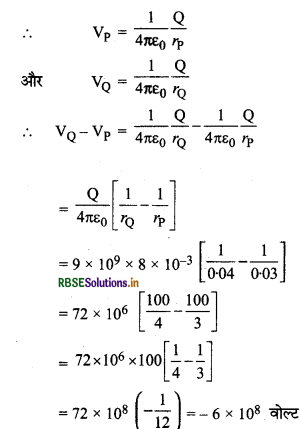
∵ आवेश q (= -2 x 10^-9 C) को P से R एवं R से होते हुए O तक ले जाया जाता है, अतः कृत कार्य मार्ग पर निर्भर न करके केवल अन्तिम बिन्दु Q एवं प्रारम्भिक बिन्दु P के मध्य विभवान्तर पर निर्भर करेगा, अत:
W = q (V_Q - V_P)
= -2 x 10^-9 (-6 x 10⁸) = 12 x 10^-1
∴ W = 1.2 J

प्रश्न 13.
b भुजा वाले एक घन के प्रत्येक शीर्ष (vertex) पर q आवेश है। इस आवेश विन्यास (charge array) के कारण घन के केन्द पर विद्युत विभव तथा विद्युत क्षेत्र ज्ञात कीजिए। 
हल: 
(a) धन के विकर्ण की लम्बाई
=\(\sqrt{b^2+b^2+b^2}=b \sqrt{3}\)
∵ घन के सभी विकर्ण कटान (point of meeting) बिन्दु (घन का केन्द्र) पर एक - दूसरे को समद्विभाजित (equally divide) करते हैं।
अतः घन के केन्द्र से प्रत्येक शीर्ष की दूरी, r = \(\frac{b \sqrt{3}}{2}\)
घन में आठ शीर्ष होते हैं और प्रत्येक शीर्ष पर समान आवेश (q) रखा है, अतः सभी शीर्षस्थ (vertex) आवेश केन्द्र पर समान विभव उत्पन्न करेंगे। 
∴ घन के जेन्द्र पर उत्पन्न कुल विद्युत् विभव
V = 8 V₁, जहाँ V₁ = एक शीर्ष पर 
आवेश के कारण विभव
= \(\begin{gathered} 8 \times \frac{1}{4 \pi \varepsilon_0} \frac{q}{r} \\ \frac{8 q}{4 \pi \varepsilon_0 \frac{\sqrt{3}}{2} b} \end{gathered}\)
∴ V = \(\frac{4 q}{\sqrt{3} \pi \varepsilon_0 b} \)

(b) सभी शीषर्षों पर समान आवेश है और केन्द्र से प्रत्येक शीर्ष की दूरी समान है, अतः प्रत्येक विकर्ण के साथ जुड़े शीर्षों के विद्युत् क्षेत्र केन्द्र पर परिमाण में समान किन्तु दिशा में विपरीत होने के कारण एक - दूसरे को निरस्त (cancel) कर देंगे।
अतः केन्द्र पर परिणामी विद्युत् क्षेत्र की तीव्रता = 0 शून्य

प्रश्न 14.
1.5 µC और 2.5 µC आवेश वाले दो सूक्ष्म गोले 30 cm दूर स्थित हैं।
(a) दोनों आवेशों को मिलाने वाली रेखा के मध्य - बिन्दु पर, और
(b) मध्य - बिन्दु से होकर जाने वाली रेखा के अभिलम्ब तल (plane normal to the line) में मध्य - बिन्दु से 10 cm दूर स्थित किसी बिन्दु पर विभव एवं विद्युत् क्षेत्र ज्ञात कीजिए।

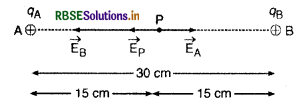
हल: 
(a) दिया है-
q_A = 1.5 µC = 1.5 x 10^-6 C
q_B = 2.5 µC = 2.5 x 10^-6 C
बिन्दु P पर विभव, V = V_A + V_B

P पर परिणामी विद्युत् क्षेत्र,

(b) चित्रानुसार,

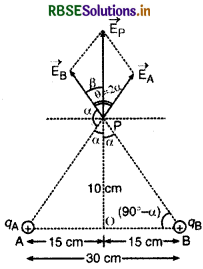
AP² = BP²
= (15)² + (10)²
= 225 + 100 = 325 = 25 x 13
∴ AP = BP 
= 5 x \(\sqrt{13}\)
= 18.02 ≈18 cm =18 x 10^-2 m
पुन: tan α = \(\frac{15}{10}\)  = 1.5
∴ α = tan-1 (1.5) = 56.3°
अत: \(\overrightarrow{\mathrm{E}_{\mathrm{A}}} \text { व } \overrightarrow{\mathrm{E}_{\mathrm{B}}}\) के मध्य कोण,
θ = 2α = 2 x 56.3 = 112.6°
अब बिन्दु P पर विद्युत् विभव,
V_P = V_A + V_B

∴ V_P = 2 x 10⁵ वोल्ट
P पर उत्पन्न विद्युत् क्षेत्र

∴ E_B = 0.694 x 10⁶ = 6.94 x 10⁵ NC^-1
अतः P पर परिणामी विद्युत् क्षेत्र की तीव्रता (समान्तर चतुर्भुज नियम से)

∴ E_P = 6.6 x 10⁵ Vm^-1
यदि परिणामी क्षेत्र E_P विद्युत् क्षेत्र E_B के साथ ß कोण बनाता है तो

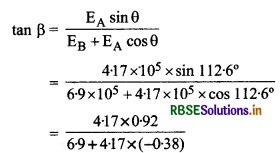
क्योंकि sin 112.6° = 0.92
और cos 112.6° = (-0.38) 
या tan ß = 0.715
∴ ß = tan-1 (0.715) = 35.6°
अतः परिणामी क्षेत्र BA दिशा के साथ बनाया गया कोण
\(\begin{aligned} \phi &=\angle \mathrm{ABP}+\beta \\ &=\left(90^{\circ}-\alpha\right)+\beta=90^{\circ}-56 \cdot 3^{\circ}+35 \cdot 6^{\circ} \end{aligned}\)
∴ \(\phi=69 \cdot 3^{\circ}\)
अतः परिणामी क्षेत्र 6.6 x 10⁵ Vm-¹ है जो BA दिशा से लगभग 69° का कोण बनाता है।

प्रश्न 15. 
आन्तरिक त्रिज्या r₁ तथा r₂ बाह्य त्रिज्या वाले एक गोलीय चालक खोल या कोश (shell) पर Q आवेश है।
(a) खोल के केन्द्र पर एक आवेशव q रखा जाता है। खोल के भीतरी (Inner) एवं बाहरी (outer) पृष्ठों पर आवेश घनत्व क्या है?
(b) क्या किसी कोटर (cavity) (जो आवेश विहीन है) में विद्युत् क्षेत्र शून्य होता है, चाहे खोल गोलीय न होकर किसी भी अनियमित (irregular) आकार का हो? स्पष्ट कीजिए।
हल: 
(a) जब किसी भी चालक को आवेश दिया जाता है तो समस्त आवेश उसके पृष्ठ पर वितरित हो जाता है। अत: कोश को दिया गया आवेश +Q कोश के बाहरी पृष्ठ पर वितरित हो जायेगा, लेकिन कोश के अन्दर रखा गया धनावेश (+q) प्रेरण के द्वारा कोश के भीतरी पृष्ठ पर (-q) आवेश उत्पन्न करेगा और यह (+q) प्रेरित आवेश कोश के बाहरी पृष्ठ पर आ जायेगा।
कोश के बाहरी पृष्ठ पर आवेश = (Q+q) 
एवं कोश के भीतरी पृष्ठ पर आवेश= -q
अतः बाहरी पृष्ठ पर आवेश का पृष्ठ घनत्व
\(\sigma_1=\frac{(\mathrm{Q}+q)}{4 \pi r_2^2}\)
और भीतरी पृष्ठ पर आवेश का पृष्ठ घनत्व
\(\sigma_2=-\frac{q}{4 \pi r_1^2}\)
(b) हाँ, कोटर (cavity) के अन्दर विद्युत् क्षेत्र शून्य होगा।

प्रश्न 16. 
(a) दर्शाइए कि आवेशित पृष्ठ के एक पार्श्व से दूसरे पार्श्व (side) पर स्थिर विद्युत् क्षेत्र के अभिलम्ब घटक (normal component) में असातत्य (discontinuity) होता है, जिसे
\(\left(\overrightarrow{\mathbf{E}_2}-\overrightarrow{\mathbf{E}_1}\right) \cdot \hat{\boldsymbol{n}} .=\frac{\sigma}{\varepsilon_0}\)
द्वारा व्यक्त किया जाता है जहाँ \(\hat{\boldsymbol{n}}\) बिन्दु पर पृष्ठ के अभिलम्ब एकांक सदिश ( normal unit vector) है तथा σ उस बिन्दु पर पृष्ठ आवेश घनत्व है (\(\hat{n}\) की दिशा पाय 1 से पावं 2 की ओर है)। अतः दर्शाइए कि चालक के ठीक बाहर विद्युत् क्षेत्र \(\frac{\sigma}{\varepsilon_0} \hat{\boldsymbol{n}}\) है।
(b) दर्शाइए कि आवेशित पृष्ठ के एक पाय से दूसरे पाश्वं पर स्थिर वैद्युत क्षेत्र का स्पर्शीय घटक (tangential component) संतत है। [संकेतः (a) के लिए गाउस नियम का उपयोग कीजिए (b) के लिए इस सत्य का उपयोग करें कि संवृत पाश पर एक स्थिर वैद्युत क्षेत्र द्वारा किया गया कार्य शून्य होता है।
हल: 
(a) माना AB एक समतल आवेशित पृष्ठ है जिस पर आवेश का पृष्ठ घनत्व σ है। आवेशित पृष्ठ AB

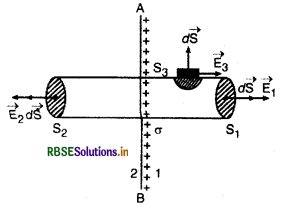
के अभिलम्बवत् आर - पार (across) एक बेलनाकार (cylinderical) गाउसीय पृष्ठ की कल्पना करते हैं जिसका एक सूक्ष्म समतल पृष्ठ S₁ फलक 1 की ओर और दूसरा S₂ फलक 2 की ओर है। गाउसीय पृष्ठ का अनुप्रस्थ क्षेत्रफल यदि है तो पृष्ठ द्वारा परिबद्ध आवेश
\(\Sigma q=\sigma . \mathbf{S}\) .......(i) 
∴ गाउस के प्रमेय से गॉसीय पृष्ठ से निर्गत विद्युत् फ्लक्स
\(\phi=\frac{1}{\varepsilon_0} \cdot \Sigma q=\frac{\sigma S}{\varepsilon_0}\)
या \(\phi=\frac{\sigma \mathrm{S}}{\varepsilon_0}\) ...................(ii)
परन्तु फ्लक्स की परिभाषा से,
\(\phi=\oint \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}\)
या \(\phi=\oint_{\mathrm{E}_1} \overrightarrow{\mathrm{E}_1} \cdot \overrightarrow{\mathrm{S}}+\oint_{\mathrm{S}_2}\) \(\overrightarrow{\mathrm{E}_2} \cdot \overrightarrow{\mathrm{S}}+\oint_{\mathrm{S}_3} \overrightarrow{\mathrm{E}_3} \cdot \overrightarrow{\mathrm{S}}\)
∵ विद्युत् क्षेत्र की दिशा आवेशित पृष्ठ की लम्ब दिशा में है, अतः
(i) सूक्ष्म पृष्ठ S₁ पर θ = 0  ∴cos θ =1
(ii) सूक्ष्म पृष्ठ S₂ पर θ = 0 ∴cos θ = 1
(iii) बेलनाकार पृष्ठ S₃ पर θ = 90° ∴ cos θ = 0 

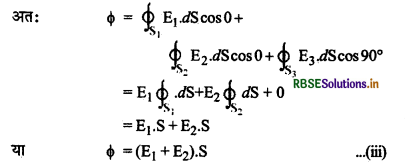
या \(\phi=\left(E_1+E_2\right) \cdot S\) ................(iii)
∴ समी. (ii) व (iii) से,
(E₁ + E₂) S =\( \frac{\sigma}{\varepsilon_0} \mathrm{~S}\)
या E₁ + E₂  \(=\frac{\sigma}{\varepsilon_0}\) ............................(iv)
यहाँ E₁ व E₂ क्रमशः \(\overrightarrow{E_1} \text { व } \overrightarrow{E_2}\) के परिमाण हैं।
यदिफलक 2 की ओर पृष्ठकेलम्बवदिशा (perpendiculardirection) में एकांक वेक्टर \(\hat{n}\) हैतो फलक 1 की ओर यह -\(\hat{n}\) होगा क्योंकि प्रश्नानुसार \(\hat{n}\) की दिशा पाच 1 से पार्श्व 2 की ओर है।
∴ \(\overrightarrow{\mathrm{E}}_2=\mathrm{E}_2 \cdot \hat{n}\) और \(\overrightarrow{\mathrm{E}}_1=-\mathrm{E}_1, \hat{n}\)
अतः \(\mathrm{E}_2=\overrightarrow{\mathrm{E}}_2 \cdot \hat{n}\) और \(\mathrm{E}_1=-\overrightarrow{\mathrm{E}}_1 \cdot \hat{n}\)
समी. (iv) से,\(-\overrightarrow{\mathrm{E}}_1 \cdot \hat{n}+\overrightarrow{\mathrm{E}}_2 \cdot \hat{n}=\frac{\sigma}{\varepsilon_0}\)
या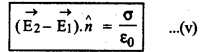
उक्त समीकरण (v) किसी आवेशित सतह के दोनों ओर स्थित बिन्द क्षेत्रों के बीच सम्बन्ध को व्यक्त करता है।
अब निम्न चित्र में प्रदर्शित अनियमित आकृति के आवेशित चालक पर विचार करते हैं। पृष्ठ के ठीक बाहर

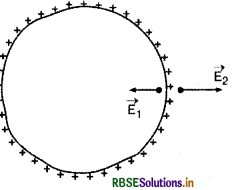
विद्युत् क्षेत्र \(\overrightarrow{\mathrm{E}}_2\) है एवं अन्दर \(\overrightarrow{\mathrm{E}_1}\) है। आवेशित चालक के अन्दर विद्युत् क्षेत्र शून्य होता है अत: E₁ = 0
अत: समी. (v) से,

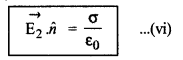
या E = E₂ =\(\frac{\sigma}{\varepsilon_0}\)
या सदिश रूप में \(\overrightarrow{\mathrm{E}}=\frac{\sigma}{\varepsilon_0} \cdot \hat{n}\)

(b) आवेशित पृष्ठ के एक ओर से दूसरी ओर जाने पर स्थिर विद्युत् क्षेत्र का स्पर्श रेखीय घटक सतत (continuous) [सर्वथा (always) शून्य] होता है, अन्यथा पृष्ठ के विभिन्न बिन्दु अलग - अलग विभवों पर होंगे तथा धनावेश पृष्ठ के अनुदिश (along) उच्च विभव से निम्न विभव के बिन्दुओं की ओर गति करता रहेगा।

प्रश्न 17. 
रैखिक आवेश घनत्व (linear charge density) λ वाला एक लम्बा आवेशित बेलन एक खोखले समाक्षीय चालक बेलन द्वारा घिरा है। दोनों बेलनों के बीच के स्थान में विद्युत् क्षेत्र कितना है?
हल: 
दोनों बेलनों के मध्य अन्दर वाले बेलन से r दूरी पर विद्युत् क्षेत्र की तीव्रता ज्ञात करने के लिए r त्रिज्या एवं l लम्बाई के बेलनाकार गाउसीय पृष्ठ (Gaussian surface) की कल्पना करते हैं। यदि आवेश का रेखीय घनत्व λ है तो गॉसीय पृष्ठ द्वारा परिबद्ध (bound) आवेश
\(\Sigma q=\lambda . l \)................(i)

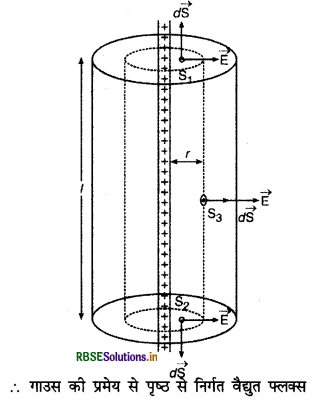
\(\phi=\frac{\boldsymbol{\Sigma} q}{\varepsilon_0}=\frac{\lambda l}{\varepsilon_0}\)
या \(\phi=\frac{\lambda l}{\varepsilon_0}\) .................(ii)
परन्तु फ्लक्स की परिभाषा से,
\(\begin{aligned} \phi &=\oint_{\mathrm{s}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}} \\ &=\oint_{\mathrm{S}} \mathrm{E} \cdot d \mathrm{~S} \cos \theta \end{aligned}\)
इस समौकरण को हल करने के लिए इसे तीन भागों में हल करते है-
(i) गाउसीय पृष्ठ का सूक्ष्म समतल अन्त्य पृष्ठ S₁ जहाँ θ = 90° ∴cos θ = 0
(ii) गाउसीय पृष्ठ का सूक्ष्म समतल अन्त्य पृष्ठ S₂ जहाँ θ = 90° ∴cos θ = 0
(iii) गाउसीय पृष्ठ का वक्र (curved) पृष्ठ S₃ जहाँ θ = 0 ∴ cos θ = 1

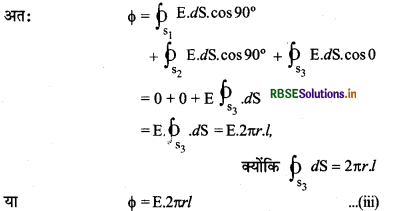
क्योंकि \(\oint_{s_3} d \mathrm{~S}=2 \pi r . l\)
या \(\phi=\mathrm{E} .2 \pi r l\) .......................(iii)
समी. (ii) व (iii) की तुलना करने पर,
\(\mathrm{E} .2 \pi r l=\frac{\lambda l}{\varepsilon_0}\)
∴ E = \(\frac{\lambda l}{2 \pi \varepsilon_0 r l}=\frac{\lambda}{2 \pi \varepsilon_0 r}\)
या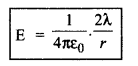
यह दोनों बेलनों के मध्य अक्ष से r दूरी पर विद्युत् क्षेत्र की तीव्रता का सूत्र है।

प्रश्न 18.
एक हाइड्रोजन परमाणु में इलेक्ट्रॉन तथा प्रोटॉन लगभग 0.53 Å दूरी पर परिबद्ध (bound) हैं।
(a) निकाय की स्थितिज ऊर्जा का eV में परिकलन कीजिए, जबकि प्रोटॉन से इलेक्ट्रॉन के मध्य अनन्त दूरी पर स्थितिज ऊर्जा को शून्य माना गया है।
(b) इलेक्ट्रॉन को स्वतन्त्र करने में कितना न्यूनतम कार्य करना पड़ेगा, यदि यह दिया गया है कि इसकी कक्षा में गतिज ऊर्जा (a) में प्राप्त स्थितिज ऊर्जा के परिमाण की आधी है।
(c) यदि स्थितिज ऊर्जा को 1.06 Å पृथक्करण (separation) पर शून्य से लिया जाए तो उपर्युक्त (a) और (b) के उत्तर क्या होंगे?
हल: 
(a) दिया है-
q₁ = -1.6 x 10^-19 C, q₂ = +1.6 x 10^-19 C
r = 0.53 Å = 0.53 x 10^-10 m = 5.3 x 10^-11 m
∴ इलेक्ट्रॉन - प्रोटॉन के निकाय की वैद्युत स्थितिज ऊर्जा

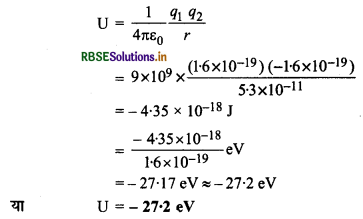
= -27.17 eV ≈ -27.2 eV
या U = -27.2 eV

(b) इलेक्ट्रॉन की स्थितिज ऊर्जा
U = -27.2 eV
तथा गतिज ऊर्जा
E_K = \(\frac{1}{2} U=\frac{1}{2} \times 27.2 \mathrm{eV} = 13.6 eV\)
यदि इलेक्ट्रॉन को मुक्त करने के लिए आवश्यक कार्य W है तो मुक्त होने पर
W + U + E_K = 0
या W = - U - E_K
= -(-27.2) eV -13.6 eV
= 27.2 - 13.6
∴ W = 13.6 eV

(c) r' = 1.06 Å  = 1.06 x 10^-10 m की दूरी पर निकाय की वैद्युत स्थितिज ऊर्जा

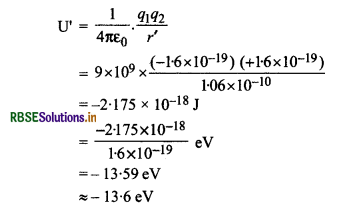
= -13.59 eV
≈ -13.6 eV
जब दूरी r' = 1.06 Å पर स्थितिज ऊर्जा शुन्य मानते हैं तो दूरी r = 0.53 Å पर निकाय की स्थितिज ऊर्जा
U'' = U - U' = -27.2 - (-13.6)
= -27.2 + 13.6 = -13.6 eV
स्पष्ट है कि निकाय की कुल ऊर्जा (U" + E_K ) शून्य हो जायेगी क्योंकि गतिज ऊर्जा
E_K = 13.6 eV अर्थात् E = U'' + E_K = 0
अतः इलेक्ट्रॉन को मुक्त करने के लिए आवश्यक कार्य
W = E - U' = 0 - (-13.6) = 13.6 eV
∴ W = 13.6 eV

प्रश्न 19. 
यदि H₂ अणु के दो में से एक इलेक्ट्रॉन को हटा दिया जाये तो हमें हाइड्रोजन आण्विक (molecular) आयन (H₂⁺) प्राप्त होगा। (H₂⁺) की निम्नतम अवस्था (ground state) में दो प्रोटॉनों के बीच की दूरी लगभग 1.5 Å  है और इलेक्ट्रॉन प्रत्येक प्रोटॉन से लगभग 1 Å  की दूरी पर है। निकाय की स्थितिज ऊर्जा ज्ञात कीजिए। स्थितिज ऊर्जा की शून्य स्थिति के चयन का उल्लेख कीजिए।
हल: 
प्रत्येक प्रोटॉन का आवेश
q₁ = q₂ = +1.6 x 10^-19 C

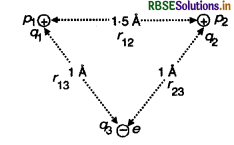
दोनों के मध्य दूरी r₁₂ = 1.5 Å
= 1.5 x 10^-10 m
इलेक्ट्रॉन का आवेश q₃ = -1.6 x 10^-19 C
प्रत्येक प्रोटॉन से इलेक्ट्रॉन की दूरी
r₁₃ = r₂₃ = 1 Å = 1 x 10^-10 m
∴  निकाय की स्थितिज ऊर्जा

या U = -19.2 eV
स्थितिज ऊर्जा अनन्त पर शून्य ली गई है।

प्रश्न 20. 
a और b त्रिज्याओं वाले दो आवेशित चालक गोले एक तार द्वारा एक - दूसरे से जोड़े गये हैं। दोनों गोलों के पृष्ठों पर विद्युत् क्षेत्रों में क्या अनुपात है? प्राप्त परिणाम को यह समझाने में प्रयुक्त कीजिए कि किसी चालक के तीक्ष्ण (sharp) एवं नुकीले सिरों (pointed ends) पर आवेश घनत्व (charge density), चपटे (Matter) भागों (portions) की अपेक्षा अधिक क्यों होता है?
हल:
दोनों गोले तार द्वारा जुड़े हैं और दोनों का विभव (V) समान होगा, अत:
V = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1}{a}=\frac{1}{4 \pi \varepsilon_0} \frac{q_2}{b}\)

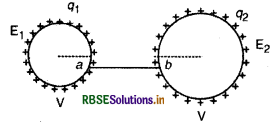
या \(\frac{q_1}{a}=\frac{q_2}{b}\)
या \(\frac{q_1}{q_2}=\frac{a}{b}\)
अब \(\mathrm{E}_1=\frac{1}{4 \pi \varepsilon_0} \frac{q_1}{a^2}\) और \(\mathrm{E}_2=\frac{1}{4 \pi \varepsilon_0} \frac{q_2}{b^2}\)
∴ \(\frac{\mathrm{E}_1}{\mathrm{E}_2}=\frac{q_1}{q_2} \times \frac{b^2}{a^2}=\frac{a}{b} \times \frac{b^2}{a^2}\), समी. (i) से
या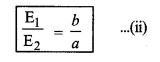
अब प्रश्न के दूसरे भाग पर विचार करना है जिसमें सिद्ध करना है कि आवेश का पृष्ठ घनत्व ∝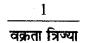
वक्रता त्रिज्या माना किसी आवेशित चालक के दो अलग - अलग भागों की वक्रता त्रिज्याएँ (radius of curvature) a और b हैं और चालक का प्रथम भाग दूसरे की अपेक्षा अधिक नुकीला है तो a < b होगा। यदि इन भागों पर आवेश के पृष्ठ घनत्व क्रमश: σ₁ व σ₂ और संचित (stored) आवेश क्रमश: q₁ व q₂ हो तो समी. (i) से,
\(\frac{q_1}{q_2}=\frac{a}{b}\)
और σ₁ = \(\frac{q_1}{4 \pi a^2}\) तथा σ₂ =\(\frac{q_2}{4 \pi b^2}\)
∴ σ₁ = \(\frac{q_1}{q_2} \times \frac{b^2}{a^2}=\frac{a}{b} \times \frac{b^2}{a^2}\)
पुनः समी. (i) से,
या\( \frac{\sigma_1}{\sigma_2}=\frac{b}{a} \Rightarrow \sigma_1 a=\sigma_2 b\)
⇒ σ.r = नियतांक 
अर्थात् σ x  वक्रता त्रिज्या = नियतांक
∴ σ =
∴ σ ∝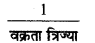
∵ a < b
∴ σ₁ > σ₂
अर्थात् नुकीले (कम वक्रता त्रिज्या वाले) भाग पर आवेश का पृष्ठ घनत्व अधिक होता है।

प्रश्न 21. 
बिन्दु (0, 0, -a) तथा (0, 0, a) पर दो आवेश क्रमशः -q और +q स्थित हैं।
(a) बिन्दुओं (0, 0, z) और (x, y, 0) पर स्थिर विद्युत् विभव क्या हैं?
(b) मूलबिन्दु से किसी बिन्दु की दूरी r पर विभव की निर्भरता (dependence) ज्ञात कीजिए, जबकि \( \frac{\boldsymbol{r}}{\boldsymbol{a}} >>1\) है।
(c) x - अक्ष पर बिन्दु (5, 0, 0) से बिन्दु (-7, 0, 0) तक एक परीक्षण आवेश को ले जाने में कितना कार्य करना होगा? यदि परीक्षण आवेश को उन्हीं बिन्दुओं के बीच x - अक्ष से होकर न ले जाएँ तो क्या उत्तर बदल जायेगा?
हल: 
दिये गये आवेश - q व +q एक वैद्युत द्विध्रुव की रचना करते हैं जिसकी लम्बाई 2a होगी।
∴ वैद्युत द्विध्रुव आघूर्ण p = q.2a
(a) प्रेक्षण बिन्दु (0, 0, z) द्विध्रुव की अक्षीय स्थिति (axial position) में होगा क्योंकि द्विध्रुव भी z - अक्ष के अनुदिश है और इसका मध्य बिन्दु मूलबिन्दु (0, 0, 0) पर है। अत: समी. V= \(\frac{1}{4 \pi \varepsilon_0} \frac{p}{\left(r^2-l^2\right)}\) के अनुसार इस बिन्दु पर विद्युत् विभव


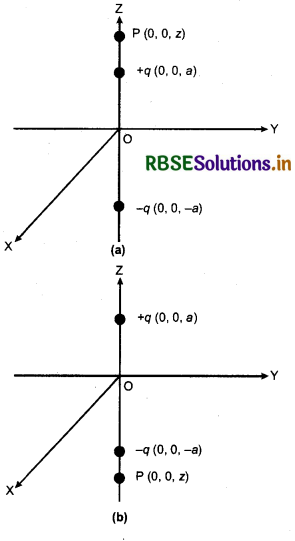
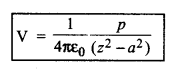
बिन्दु (x, y, 0) द्विध्रुव की निरक्षीय स्थिति में स्थित होगा अत: इस बिन्दु पर विद्युत् विभव = 0 (शून्य) 

(b) द्विध्रुव के कारण किसी बिन्दु पर विद्युत विभव:
माना कोई बिन्दु P, द्विध्रुव के केन्द्र (मूल बिन्दु) से r दूरी पर स्थित है। इस बिन्दु की बिन्दु आवेशों +q तथा -q से दूरियाँ क्रमश: r₁ तथा r₂ हैं। तब बिन्दु P पर द्विध्रुव के कारण विद्युत विभव
V = \(\frac{1}{4 \pi \varepsilon_0}\left(\frac{q}{r_1}-\frac{q}{r_2}\right)\) .............(i)
माना \(\angle Z O P=\theta\) तब
∆OBP में,
r₁² = r² + a² - 2ar cosθ ...(2)
तथा AAOP में,
r₂² = r² + a² -2ar cos (180 - θ)
या r₂² = r² + a² + 2ar cosθ .............(3)
∴ समीकरण (2) से, 
r₁² = r² \(\left(1-\frac{2 a}{r} \cos \theta+\frac{a^2}{r^2}\right)\)
≈ r² \(\left(1-\frac{2 a}{r} \cos \theta\right)\) [\(\frac{r}{a}>>1\) मानते हुए \(\frac{a}{r}\) द्विघात पद छोड़ने पर}]
इसी प्रकार r₂² ≈ r² \(\left(1+\frac{2 a}{r} \cos \theta\right)\)
∴ \(\frac{1}{r_1} \approx \frac{1}{r}\left(1-\frac{2 a}{r} \cos \theta\right)^{-1 / 2}\)
या \(\frac{1}{r_1} \approx \frac{1}{r}\left(1+\frac{a}{r} \cos \theta\right)\) (द्विपद प्रमेय से)
इसी प्रकार \(\frac{1}{r_2} \approx \frac{1}{r}\left(1-\frac{a}{r} \cos \theta\right)\)
∴ समीकरण (1) में मान रखने पर,
V  \(\begin{aligned} &=\frac{1}{4 \pi \varepsilon_0} \frac{q}{r} \times \frac{2 a}{r} \cos \theta \\ &=\frac{1}{4 \pi \varepsilon_0} \frac{(2 q a) \cos \theta}{r^2} \end{aligned}\)
अत: द्विध्रुव के कारण उसके केन्द्र से दूरी पर \(\left(\frac{r}{a}>>1\right)\) विद्युत विभव
V = \(\frac{p \cos \theta}{4 \pi \varepsilon_0 r^2} \) जहाँ p = 2qa
परन्तु p cosθ = \(\vec{p} \cdot \hat{r}\) जहाँ \(\hat{r}, \vec{r}\) की दिशा में एक सदिश है।
∴ V = \(\frac{\overrightarrow{\mathrm{p}} \cdot \hat{\mathrm{r}}}{4 \pi \varepsilon_0 r^2}\)

(c) बिन्दु P(5, 0, 0) तथा Q(-7, 0, 0) द्विध्रुव की निरक्षीय स्थिति में होंगे अतः इन पर विद्युत् विभव शून्य होगा।
∴ परीक्षण आवेश q₀ को P से Q तक ले जाने में कृत कार्य
W= q₀ (VQ - VP) = q₀ x 0 = 0 (शून्य) 
∵ विद्युत् क्षेत्र एक संरक्षी क्षेत्र (conservative field) है जिसमें किसी आवेश को एक बिन्दु से दूसरे बिन्दु तक ले जाने में किया गया कार्य केवल प्रथम एवं अन्तिम बिन्दु के विभव पर निर्भर करता है, मार्ग पर नहीं।
∴ उत्तर में कोई परिवर्तन नहीं आयेगा।

प्रश्न 22. 
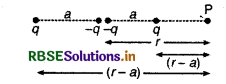
नीचे दिए गए चित्र में एक आवेश विन्यास (charge array) जिसे विद्युत् चतुर्युवी कहा जाता है, दर्शाया गया है। चतुर्भुवी (electric quadrupole) के अक्ष पर स्थित किसी बिन्दु के लिए पर विभव की निर्भरता (dependence) प्राप्त कीजिए जहाँ \(\frac{r}{a} >>1\). अपने परिणाम की तुलना एक विद्युत् वधुव व विद्युत् एकल ध्रुव (monopoles) (अर्थात् एकल आवेश) के लिए प्राप्त परिणामों से कीजिए।

हल: 
प्रेक्षण विन्दु P की विभिन आवेशों से दूरियाँ चित्र में दिखायी गई हैं। 
∴ चतुर्भुवी के कारण P पर विद्युत् विभव

∵ दिया है:\( \frac{r}{a} \gg 1\) या \(\frac{a}{r} \ll 1\)
अतः \(\frac{a^2}{r^2}<<<1\)
∴ \(\frac{a^2}{r^2}\) को छोड़ने पर,
V \(\begin{aligned} &=\frac{q}{4 \pi \varepsilon_0} \frac{2 a^2}{r^3} \\ &=\frac{1}{4 \pi \varepsilon_0} \frac{(q \cdot 2 a) a}{r^3} \end{aligned}\)
या V =\(\frac{1}{4 \pi \varepsilon_0} \frac{p a}{r^3}\)
स्पष्ट है कि \(\mathrm{V} \propto \frac{1}{r^3}\)
वैद्युत द्विध्रुव के कारण अशीय स्थिति में दीर्घ दूरियों के लिए
V = \(\frac{1}{4 \pi \varepsilon_0} \frac{p}{r^2}\)     ∴ \(\mathrm{V} \propto \frac{1}{r^2}\)
एकल द्विध्रुव (monopoles) के कारण विभव
V = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r}\)          ∴\( \mathrm{V} \propto \frac{1}{r}\)
स्पष्ट है कि चतुर्धवी के कारण विभव द्विधूव एवं एकल धुव के विभव की अपेक्षा अधिक तेजी से घटता है।

प्रश्न 23. 
एक वैद्युत टेक्नीशियन को 1kV विभवान्तर के परिपथ में 2 µF संधारित्र की आवश्यकता है। 1 µF के संधारित्र से प्रचुर संख्या (large number) में उपलब्ध हैं जो 400 V से अधिक का विभवान्तर सहन (withstand) नहीं कर सकते। कोई सम्भव विन्यास (possible arrangement) सुझाइए जिसमें न्यूनतम संधारित्रों की आवश्यकता हो।
हल: 
दिये गये संधारित्र की धारिता C₁ = 1 µF और अधिकतम वोल्टता = 400 V, लेकिन टेक्नीशियन को 1kV के लिए परिणामी धारिता 2 µF चाहिए। इसके लिए प्रयुक्त विन्यास में माना n - संधारित्रों के श्रेणी संयोजनों को m पंक्तियाँ समान्तर क्रम में जोड़ी जाती हैं।
एक पंक्ति का विभवान्तर 1 kV अर्थात् 1000 V 
n संधारित्रों में समान रूप से बैट जायेगा, अत: 
प्रत्येक संधारित्र पर विभवान्तर = \(\frac{1000}{n}\) वोल्ट
यह विभवान्तर 400 वोल्ट से कम ही रहेगा क्योंकि 400 V तो अधिकतम वोल्टता है 
∴ \(\frac{1000}{n}<400\) या \(\frac{1000}{400}<n\)
या 2.5 < n
∵ n न्यूनतम पूर्णांक है अतः n = 3
अर्थात् एक पंक्ति में तीन संधारित्र श्रेणीबद्ध हैं। 
अतः एक पंक्ति की धारिता C'' =\( \frac{\mathrm{C}_1}{3}\) µF
इसी धारिता C' की m पंक्तियाँ समान्तरबद्ध हैं अतः तुल्य धारिता
C = C' + C' + ..................+ C' (m तक) = mC'
या C = mC' = m x \(\frac{\mathrm{C}_1}{3}\)
∴ mC₁  = 3C ⇒ m = \(\frac{3 \mathrm{C}}{\mathrm{C}_1}=\frac{3 \times 2}{1} = 6\)
या m = 6
इस प्रकार 3 - 3 संधारित्रों के श्रेणी संयोजन की 6 पंक्तियाँ समान्तरबद्ध करनी होगी।

प्रश्न 24. 
2F वाले एक समान्तर पट्टिका संधारित्र का क्षेत्रफल क्या है, जबकि पट्टिकाओं का पृचकन 0.5 cm है?
[अपने उत्तर से आप यह समझ पाएंगे कि सामान्य संधारित्र µF या कम परिसर के क्यों होते हैं? तथापि विद्युत अपघटन संधारित्रों (Electrolytic Capacitors) की धारिता कहीं अधिक (0.1F) होती है क्योंकि चालकों के बीच अति सूक्ष्म पृथकन होता है।
हल: 
दिया है: d = 0.5 cm = 0.5 x 10^-2 m = 5 x 10^-3 m
धारिता C = 2F , क्षेत्रफल A = ?
∵ समान्तर प्लेट संधारित्र की धारिता
C =\( \frac{\mathrm{A \varepsilon}_0}{d} ⇒ A = \frac{\mathrm{C} . d}{\varepsilon_0}\)
∴ A = \(\frac{2 \times 5 \times 10^{-3}}{8.854 \times 10^{-12}}\)
= 1.13 x 10⁹ m²
= 1130 x 10⁶ m² = 1130 km²

प्रश्न 25. 
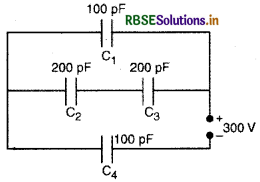
चित्र के नेटवर्क (जाल) की तुल्य घारिता (equivalent capacitance) प्राप्त कीजिए। 300 V संभरण (supply) के साथ प्रत्येक संधारित्र का आवेश व उसकी वोल्टता ज्ञात कीजिए।

हल: 
दिया गया नेटवर्क चित्र में दिये गये नेटवर्क के तुल्य है।

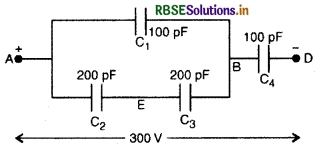
\(\mathrm{C}_2 \text { व } \mathrm{C}_3\) के श्रेणी संयोजन की धारिता
या \(\frac{1}{\mathrm{C}^{\prime}}=\frac{2}{200}=\frac{1}{100}\)
या C' = 100 pF
∵ A व B के मध्य C₁ व C' समान्तरबद्ध हैं, अत: A व B के मध्य धारिता
C'' = C' + C₁ = 100 + 100 = 200 pF
अब पूरे संयोजन की धारिता अर्थात् A व D के मध्य धारिता
\(\frac{1}{\mathrm{C}}=\frac{1}{\mathrm{C}^{\prime \prime}}+\frac{1}{\mathrm{C}_4}=\frac{1}{200}+\frac{1}{100}=\frac{3}{200}\)
∴ C = \(\frac{200}{3}\) pF
संयोजन पर संचित कुल आवेश
q = CV = \(\frac{200}{3} \times 10^{-12} \times 300\)
या q = 2 x 10^-8 C
C₂ व C₃ पर संचित आवेश परिमाण में समान होंगे अर्थात
q₂ = q₃
∴ q₁ + q₂ = q, जहाँ C₁ पर संचित आवेश q₁ है।
∴ q₁ +q₂ = 2 x 10^-8 ...................(i)
∵ V_AB = \(\frac{q_1}{\mathrm{C}_1}=\frac{q_2}{\mathrm{C}^{\prime}}\)
⇒ \(\frac{q_1}{100}=\frac{q_2}{100}\) ⇒ q₁ = q₂
∴ समी. (i) से,
q₁ + q₁ = 2 x 10^-8
या 2q₁ = 2 x 10^-8  ⇒ q₁ = 1 x 10^-8 C
∴ q₂ = q₃ = q₁ = 1 x 10^-8 C
∵ V = \(\frac{q}{\mathrm{C}}\) ∴ V₁ = \(\frac{q_1}{C_1}=\frac{1 \times 10^{-8}}{100 \times 10^{-12}}\) = 100 V
V₂ = \(\frac{q_2}{C_2}=\frac{1 \times 10^{-8}}{200 \times 10^{-12}}\) = 50 V
इसी प्रकार V₃ = \(\frac{q_3}{\mathrm{C}_3}\) =50v
V₄ = \(\frac{q_4}{\mathrm{C}_4}=\frac{2 \times 10^{-8}}{100 \times 10^{-12}}\) = 200 V
अतः संयोजन की धारिता = \(\frac{200}{3}\) pF 
C₁ पर संचित आवेश = 1 x 10^-8 C
और विभवान्तर = 100 V
C₂ पर संचित आवेश = 1 x 10^-8 C
और विभवान्तर = 50 V
C₃ पर संचित आवेश = 1 x 10^-8 C
और विभवान्तर = 50 V
C₄ पर संचित आवेश = 2 x 10^-8 C
और विभवान्तर = 200 V

प्रश्न 26. 
किसी समान्तर प्लेट संधारित्र की प्रत्येक प्लेट का क्षेत्रफल 90 cm2 है और उनके बीच प्रथकन (separation) 2.5 mm है। 400 V संभरण (supply) से संधारित्र को आवेशित किया गया है।
(a) संधारित्र कितनी स्थिर - विद्युत् ऊर्जा संचित करता है?
(b) इस ऊर्जा को प्लेटों के बीच स्थिर - विद्युत् क्षेत्र में संचित समझकर प्रति एकांक आयतन ऊर्जा u ज्ञात कीजिए। इस प्रकार प्लेटों के बीच विद्युत् क्षेत्र E के परिमाण और u में सम्बन्ध स्थापित कीजिए। 
हल: 
दिया है-
A = 90 cm²
= 90 x 10^-4 m²
= 90 x 10^-3 m²,
d = 2.5 mm
=2.5 x 10^-3 m,
V = 400 वोल्ट,
U = ?, u = ?, u व E के मध्य सम्बन्ध = ? 
(a) संधारित्र में संचित ऊर्जा
\(\begin{aligned} &\mathrm{U}=\frac{1}{2} \mathrm{CV}^2=\frac{1}{2} \times \frac{\mathrm{A \varepsilon}_0}{d} \times \mathrm{V}^2 \\ &\mathrm{U}=\frac{9 \times 10^{-3} \times 8.854 \times 10^{-12} \times 400 \times 400}{2 \times 2.5 \times 10^{-3}} \end{aligned}\)
∴ U = 2.55 x 10^-6 J

(b) संधारित्र का आयतन
= A.d = 9 x 10^-3 x 2.5 x 10^-13
= 22.5 x 10^-6 m³
∴ संधारित्र के एकांक आयतन में संचित ऊजाँ
u = \(\frac{U}{\text { आयतन }}=\frac{2.55 \times 10^{-6}}{22.5 \times 10^{-6}}\)
= 0.113 Jm-3


प्रश्न 27. 
एक 4 µF के संधारित्र को 200 V संभरण से आवेशित (charged) किया गया है। फिर संभरण से हटाकर (disconnect) इसे एक अन्य अनावेशित (uncharged) 2 µF के संधारित्र से जोड़ा जाता है। पहले संधारित्र की कितनी स्थिर - विद्युत् ऊर्जा का ऊष्मा और विद्युत् - चुम्बकीय विकिरण (electromagnetic radiation) के रूप में ह्रास (loss) होता है? 
हल: 
दिया है-
C₁ = 4 µF = 4 x 10^-6 F, V₁ = 200 वोल्ट
C₂ = 2 µF = 2 x 10^-6, V₂ = 0
दोनों को जोड़ने पर ऊर्जा में ह्र्रस

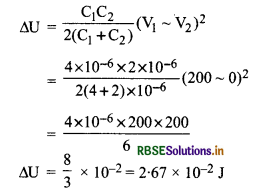
∴ ∆U = 2.67 x 10^-2 J

प्रश्न 28. 
दर्शाइए कि एक समान्तर प्लेट संधारित्र की प्रत्येक प्लेट पर बल का परिमाण \(\frac{1}{2}\) QE है, जहाँ Q संधारित्र पर आवेश है और E पटिट्काओ के मध्य विद्युत् क्षेत्र का परिमाण है। घटक (factor) 1 / 2 के मूल (origin) को समझाइए।
हल:
माना दोनों प्लेटों के बीच लगने वाला पारस्परिक आकर्षण बल F है तथा प्लेटों के बीच दूरी है। दूरी x में dx की वृद्धि करने पर आकर्षण बल F के विरुद्ध किया गया कार्य
 dW = F.dx ...........(i)
संधारित्र के प्रति एकांक आयतन में संचित ऊर्जा
u = \(\frac{1}{2} \varepsilon_0 \mathrm{E}^2\)
∵ आयतन = A.x
∴ U = u x आयतन
= u x (Ax)
= \(\frac{1}{2} \varepsilon_0 \mathrm{E}^2 \cdot(\mathrm{A} x)\)
∴ प्लेटों के मध्य दूरी x में dx वृद्धि करने पर ऊर्जा में वृद्धि
dU = \(\frac{1}{2} \varepsilon_0 \mathrm{E}^2 \cdot \mathrm{A} \cdot d x\)
∵ प्लेटों के मध्य दूरी बढ़ाने में किया गया कार्य ही संधारित्र की में निहित हो जाता है।
∴ dU = dW
या F.dx = \(\frac{1}{2} \varepsilon_0 \mathrm{E}^2 \cdot \mathrm{A} \cdot d x\)
या F = \(\frac{1}{2} \varepsilon_0 E^2 \cdot A.\)
या F = \(\frac{1}{2} \mathrm{E}\left(\varepsilon_0 \mathrm{E} . \mathrm{A}\right)\) ..........(ii)
∵ E =\(\frac{\sigma}{\varepsilon_0}=\frac{Q}{A \varepsilon_0}\)
⇒ Q = E.Aε0
∴ समी (ii) से,

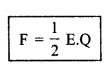
घटक \(\frac{1}{2}\) का मूल इस तथ्य में निहित (lies in the fact) है कि चालक प्लेट के बाहर विद्युत् क्षेत्र E तथा प्लेट के अन्दर शून्य होता है, अत: औसत विद्युत् क्षेत्र \(\frac{0+\mathrm{E}}{2}=\frac{1}{2} \mathrm{E}\) होता है, जिसके विरुद्ध प्लेट को खिसकाया जाता है।

प्रश्न 29. 
दो समकेन्द्रीय (concentric) गोलीय चालकों जिनको उपयुक्त विद्युतरोधी (insulating) आलम्बों (supports) से उनकी स्थिति में रोका गया है, से मिलकर एक गोलीय संधारित्र बना है। दर्शाइए कि गोलीय संधारित्र की घारिता C इस प्रकार व्यक्त की जाती है-

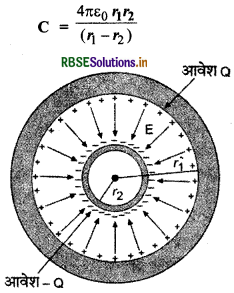
जहाँ r₁ व r₂ क्रमशः बाहरी तथा भीतरी गोलों की त्रिज्याएँ हैं।
उत्तर: 
गोलाकार संधारित्र की धारिता (Capacity of Spherical Capacitor) 
गोलाकार संधारित्र की रचना चित्र 2.37 में दिखायी गई है। इसमें दो समकेन्द्रीय (concentric) गोलीय प्लेटें A व B होती है। बाहरी प्लेट B को पृथ्वी से सम्बन्धित किया जाता है और भीतरी प्लेट A को+आवेश दिया जाता है। बाहरी गोले पर प्रेरण द्वारा उत्पन्न धनात्मक आवेश पृथ्वी में चला जाता है और केवल ऋणात्मक आवेश रह जाता है। अत:

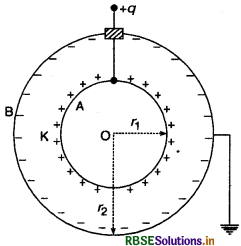
भीतरी गोले पर उत्पन्न विभव
V = V₁ + V₂
जहाँ V₁ = भीतरी गोले के +q आवेश के कारण उत्पन्न विभव = \(+\frac{1}{4 \pi \varepsilon_0 \mathrm{~K}} \frac{q}{r_1}\)
और V₂ = बाहरी गोले के - q आवेश के कारण उत्पन्न विभव = \(- \frac{1}{4 \pi \varepsilon_0 \mathrm{~K}} \cdot \frac{q}{r_2}\)

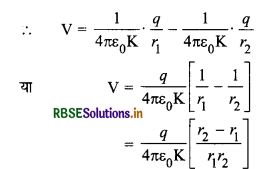
चूंकि बाहरी गोला पृथ्वी से सम्बन्धित है अतः इसका विभव शून्य होगा।
∴ दोनों गोलों के मध्य विभवान्तर = V - 0 = V
∴ संधारित्र की धारिता C =\( \frac{q}{\mathrm{~V}}=\frac{q}{\frac{q}{4 \pi \varepsilon_0 \mathrm{~K}} \frac{\left(r_2-r_1\right)}{r_1 r_2}}\)
∴
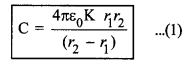
वायु संधारित्र के लिए K = 1

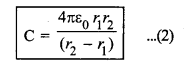
समीकरण (1) से स्पष्ट है कि गोलाकार संधारित्र को धारिता निम्न प्रकार बढ़ायी जा सकती है-
(i) गोलों की त्रिज्याएँ r₁ व r₂ बड़ाकर, लेकिन यह संधारित्र के सिद्धान्त के विरुद्ध है, अत: त्रिज्याएँ बढ़ाकर धारिता नहीं बढ़ायी जाती हैं।
(ii) C ∝K अर्थात् दोनों गोलों के मध्य अधिक परावैद्युतांक (dielectric constant) वाला परावैद्युत माध्यम (dielectric medium) रखकर धारिता बढ़ायी जा सकती है।
(iii) \(\mathrm{C} \propto \frac{1}{\left(r_2-r_1\right)}\) अर्थात् दोनों गोलों के मध्य दूरी घटाकर धारिता बढ़ाई जा सकती है।

प्रश्न 30. 
एक गोलीय संधारित्र के भीतरी गोले की त्रिज्या 12 cm है तथा बाहरी गोले की त्रिज्या 13 cm है। बाहरी गोला भू - सम्पर्कित (earthed) है और भीतरी गोले पर 2.5µC का आवेश दिया गया है। संकेन्द्री गोलों के बीच के स्थान में 32 परावैधुतांक का दव भरा है।
(a) संधारित्र की बारिता ज्ञात कीजिए। 
(b) भीमरी गोले का विभव क्या है?
(c) इस संधारित्र की धारिता की तुलना एक 12 cm वाले किसी वियुक्त (isolated) गोले की धारिता से कीजिए। व्याख्या कीजिए कि गोले की धारिता इतनी कम क्यों है? 
हल: 
दिया है- r₁ = 13 cm = 0.13 m,
r₂ = 12 cm = 0.12 m,
K = 32,
Q = 2.5 µC = 2.5 x 10^-6 C
(a) गोलाकार संधारित्र की धारिता
C = \(4 \pi \varepsilon_0 \mathrm{~K} \frac{r_1 r_2}{\left(r_1-r_2\right)}\)
\(\begin{aligned} &=\frac{32}{9 \times 10^9} \frac{(0.13 \times 0.12)}{(0.13-0.12)} \\ &=\frac{32 \times 0.13 \times 0.12 \times 10^{-9}}{9 \times 0.01} \end{aligned}\)
= 5.546 x 10^-9 F = 5.55 x 10^-9 F

(b) संधारित्र की प्लेटों के मध्य विभवान्तर
V = \(\frac{\mathrm{Q}}{\mathrm{C}}=\frac{2 \cdot 5 \times 10^{-6}}{5 \cdot 55 \times 10^{-9}}\) = 450 वोल्ट
∵ बाहरी गोला भू - सम्पर्कित है, अतः इसका विभव शून्य होगा। 
यदि भौतरौ गोले का विभव V₁ है तो
∴ V₁ = V = 450 वोल्ट
अतः भीतरी गोले का विभव = 450 वोल्ट

(c) ∵ विलगित गोले को धारिता
C' = \(4 \pi \varepsilon_0 r\)
या \(\mathrm{C}^{\prime}=\frac{r}{9 \times 10^9}=\frac{0 \cdot 12}{9 \times 10^9}=\frac{12 \times 10^{-11}}{9}\)
या \(C^{\prime}=\frac{4}{3} \times 10^{-11} \mathrm{~F}=1 \cdot 3 \times 10^{-11} \mathrm{~F}\)
∴ \(\begin{aligned} \frac{C}{C^{\prime}} &=\frac{5 \cdot 55 \times 10^{-9}}{1 \cdot 3 \times 10^{-11}} \\ &=\frac{555}{130} \times 10^2=4.269 \times 10^2=4.27 \times 10^2 \end{aligned}\)
या \(\frac{\mathrm{C}}{\mathrm{C}^{\prime}}\) = 4.27  ⇒ C = 4.27 C'
अर्थात गोलाकार संधारित्र की धारिता एकल गोले को धारिता से 427 गुनी अधिक है। इससे यह निष्कर्ष प्राप्त होता है कि एकल चालक के समीप एक अन्य भू - सम्पर्कित चालक रख कर उनके बीच के स्थान में परावैद्युत माध्यम भरने पर धारिता बहुत अधिक बढ़ जाती है। यही संधारित्र का सिद्धान्त है।

प्रश्न 31. 
सावधानीपूर्वक उत्तर दीजिए।
(a) दो बड़े चालक गोले जिन पर आवेश Q₁ व Q₂ हैं, एक - दूसरे के समीप लाये जाते हैं। क्या उनके बीच स्थिर - वैद्युत बल का परिमाण (result) तथ्यतः
\(\frac{Q_1 Q_2}{4 \pi \varepsilon_0 r^2}\)
द्वारा दर्शाया जाता है, जहाँ r उनके केन्द्रों के मध्य दूरी है?
(b) यदि कूलॉम नियम में \(\frac{1}{r^3}\) निर्भरता (dependence) का समावेश (inclusion) ( \(\frac{1}{r^2}\) के स्थान पर) हो तो क्या गाउस का नियम अभी भी सत्य होगा?
(c) स्थिर - वैद्युत क्षेत्र विन्यास (configuration) में एक छोटा परीक्षण आवेश किसी बिन्दु पर विराम में छोड़ा जाता है। क्या यह उस बिन्दु से होकर जाने वाली क्षेत्र रेखा के अनुदिश चलेगा?
(d) इलेक्ट्रॉन द्वारा एक वृत्तीय कक्षा पूरी करने में नाभिक के क्षेत्र द्वारा कितना कार्य किया जाता है? यदि कक्षा दीर्घवृत्तीय हो तो क्या होगा?
(e) हमें ज्ञात है कि एक आवेशित चालक के आर-पार विद्युत् क्षेत्र असंतत (discontinuous) होता है। क्या वहाँ विद्युत् विभव भी असंतत होगा?
(f) किसी एकल चालक की बारिता से आपका क्या अभिप्राय (mean) है?
(g) एक सम्भावित उत्तर की कल्पना कीजिए कि पानी का परावैद्युतांक (= 80), अभ्रक के परावैद्युतांक (= 6) से अधिक क्यों होता है?
उत्तर:
(a) यदि दोनों गोले काफी अधिक दूरी पर होंगे, तभी वे बिन्दु आवेशों की भांति व्यवहार करेंगे। कुलॉम का नियम केवल बिन्दु आवेशों के लिए सत्य है; अत: गोलों को समीप लाने पर कूलॉम का नियम लागू नहीं होगा।
(b) नहीं, गाउस का नियम केवल तभी तक सत्य है जब तक कि कूलॉम के नियम में निर्भरता \(\left(\frac{1}{r^2}\right)\) है, अत: कूलॉम के नियम में निर्भरता \((\left(\frac{1}{r^3}\right)\) होने पर गाउस का नियम लागू नहीं होगा।
(c) नहीं, यदि क्षेत्र रेखा एक सरल रेखा है, केवल तभी परीक्षण आवेश क्षेत्र रेखा के अनुदिश चलेगा।
(d) शून्य, स्थिर - विद्युत् क्षेत्र में बिन्दु आवेश को बन्द वक्र पर चलाने में किया गया कार्य शून्य होता है। यदि वक्र दीर्घवृत्ताकार है, तब भी कार्य शून्य होगा।
(e) नहीं, चालक की पूरी सतह पर विद्युत् विभव सतत होता है।
(f) एकल चालक की धारिता एक ऐसे संधारित्र की धारिता के तुल्य है जिसकी दूसरी प्लेट अनन्त पर होती है।
(g) जल के अणुओं का अपना स्थायी द्विध्रुव आपूर्ण होता है, अत: जल का परावैद्युतांक उच्च होता है। इसके विपरीत अभ्रक के अणुओं का द्विध्रुव आघूर्ण शून्य होता है, इसीलिए इसका परावैद्युतांक कम होता है।

प्रश्न 32. 
एक बेलनाकार संधारित्र में 15 cm लम्बाई एवं त्रिज्याएँ 1.5 cm तथा 1.4 cm के दो समास बेलन हैं। बाहरी बेलन भू - सम्पर्कित (earthed) है और भीतरी बेलन को 3.5 µC का आवेश दिया गया है। निकाय की धारिता और भीतरी बेलन का विभव ज्ञात कीजिए। अन्त्य प्रभाव (end effect) (अर्थात् सिरों पर क्षेत्र रेखाओं का मुड़ना) की उपेक्षा (neglect) कर सकते हैं।
हल: 
बेलनाकार संधारित्र को धारिता
C = \(2 \pi \varepsilon_0 \frac{l}{2.303 \log _{10}\left(\frac{b}{a}\right)}\)
प्रश्न से, l = 0.15 m, a = 1.4 cm = 1.4 x 10^-2 m
b = 1.5 cm = 1.5 x 10^-2 m,
Q = 3.5 µC = 3.5 x 10^-6 C
∴ C \(\begin{aligned} &=\frac{1}{2 \times 9 \times 10^9} \times \frac{0.15}{2.303 \log _{10}\left(\frac{1.5}{1.4}\right)} \\ &=\frac{0.15}{18 \times 10^9 \times 2.303 \times 0.0299} \end{aligned}\)
= 1.21 x 10^-10 F
= 1.21 x 10^-12 F = 121 pF
संधारित्र की प्लेटों के मध्य विभवान्तर
V = \(\frac{Q}{C}=\frac{3.5 \times 10^{-6}}{1.2 \times 10^{-10}}\)
= 2.916 x 10⁴ = 2.92 x 10⁴ वोल्ट
∵ बाहरी बेलन भू - सम्पर्कित है, अत: इसका विभव = 0 
∴ यदि भीतरी बेलन का विभव V1 हो तो
V = V₁ = 0 ⇒ V₁ = V
∴ V₁ = 2.92 x 10⁴ वोल्ट

प्रश्न 33.
3 परावैद्युतांक तथा 107 Vm^-1 की परावैद्युत सामर्थ्य (dielectric strength) वाले एक पदार्थ से 1 kV वोल्टता अनुमतांक (voltage rating) के समान्तर प्लेट संधारित्र की अभिकल्पना (designe) करनी है। [परावैद्युत सामर्थ्य वह अधिकतम विद्युत् - क्षेत्र है जिसे कोई पदार्थ बिना भंग (breakdawn) हुए अर्थात् आंशिक आयनन द्वारा बिना विद्युत् संचरण आरम्भ किये सहन कर सकता है। सुरक्षा की दृष्टि (for safety) से क्षेत्र को कभी भी परावैद्युत सामर्थ्य के 10% से अधिक नहीं होना चाहिए।] 50 pF बारिता के लिए पट्टिकाओं का कितना न्यूनतम क्षेत्रफल होना चाहिए?
हल:
K = 3, परावैद्युत सामर्थ्य = 10⁷ Vm^-1, धारिता c = 50 pF = 50 x 10^-12 F 
प्लेटों का न्यूनतम क्षेत्रफल A= ?,V= 1 kV = 1000 वोल्ट 
प्लेटों के मध्य अधिकतम विद्युत् क्षेत्र 
Emax = परावैद्युत सामर्थ्य का 10%
=\(\frac{10}{100} \times 10^7=10^6 \mathrm{Vm}^{-1}\)
यदि प्लेटों के मध्य दूरी d है तो
E_max = \(\frac{\mathrm{V}}{d} \Rightarrow d=\frac{\mathrm{V}}{\mathrm{E}_{\max }}=\frac{1000}{10^6}=10^{-3} \mathrm{~m}\)
∵ C =\( \frac{\mathrm{KA}_0}{d} \Rightarrow \mathrm{A}=\frac{\mathrm{C} . d}{\mathrm{~K} \varepsilon_0}\)
∴ A = \(\frac{50 \times 10^{-12} \times 10^{-3}}{3 \times 8.854 \times 10^{-12}}\)
= 1.88 x 10^-3 m²
=18.8 x 10^-4 m²
= 18.8 x 10^-4 x 10⁴ cm² = 18.8 cm²
∴A = 18.8 cm² ≈ 19 cm²

प्रश्न 34. 
व्यवस्थात्मकतः (describe schematically) निम्नलिखित में संतत समविभव पृष्ठ (continuous equipotential surface) का वर्णन कीजिए-
(a) z - दिशा में अचर (constant) विद्युत् क्षेत्र,
(b) एक क्षेत्र जो एक समान (uniformly) रूप से बढ़ता है, परन्तु एक ही दिशा (मान लीजिए z - दिशा) में रहता है।
(c) मूलबिन्दु (origin) पर कोई एकल (single) धनावेश और
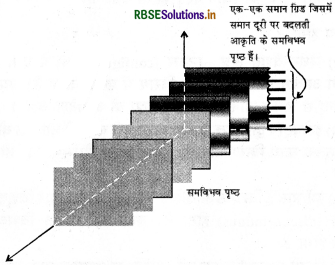
(d) एक समतल में समान दूरी पर समान्तर लम्बे आवेशित तारों से बने एकसमान जाल (uniform grid)।
उत्तर:
(a) X - Y तल के समान्तर समतल।

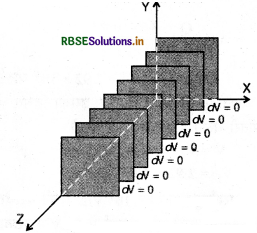
(b) समविभव पृष्ठ X - Y तल के समान्तर होंगे, परन्तु बढ़ते क्षेत्र के साथ, भिन्न - भिन्न नियत विभव वाले समतल क्षेत्र एक -दूसरे के समीप होते जायेंगे।

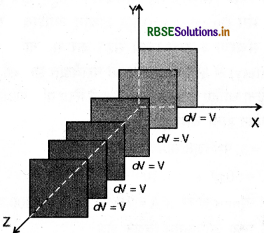
(c) समकेन्द्रीय (concentric) गोले जिनके केन्द्र मूल बिन्दु पर होंगे।

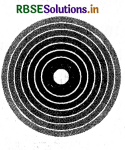
(d) जाल (grid) के समीप, समविभव पृष्ठों की आकृति समय के साथ बदलेगी परन्तु ग्रिड से दूर जाने पर समविभव पृष्ठ ग्रिड के अधिकाधिक (more and more) समान्तर होते जायेंगे।

प्रश्न 35.
r₁ त्रिज्या तथा q₁ आवेश वाला एक छोटा गोला r₂ त्रिज्या और q₂ आवेश वाले गोलीय कोश से घिरा (enclosed) है। दर्शाइए यदि q₁ बदि का धनात्मक है तो (जब दोनों को एक तार द्वारा जोड़ दिया जाता है) आवश्यक रूप से आवेश गोले से (खोल) कोश की तरफ ही प्रवाहित होगा, चाहे खोल पर आवेश q₂ कुछ भी हो।
उत्तर:
हम जानते हैं कि किसी आवेशित चालक का समस्त आवेश उसके पृष्ठ पर वितरित रहता है, अत: गोले को कोश से तार द्वारा जोड़ने पर दोनों एक चालक की तरह व्यवहार करेंगे। फलस्वरूप आवेश गोले से कोश की और ही प्रवाहित होगा चाहे q₂ का मान कुछ भी क्यों न हो।

प्रश्न 36. 
निम्न का उत्तर दीजिए- 
(a) पृथ्वी के पृष्ठ के सापेक्ष वायुमण्डल की ऊपरी परत (top layer) लगभग 400 kV पर है, जिसके संगत विद्युत् - क्षेत्र ऊँचाई बढ़ने के साथ कम होता है। पृथ्वी के पृष्ठ के सापेक्ष विद्युत्-क्षेत्र लगभग 100Vm^-1 है, तो जब हम घर से बाहर खुले में जाते हैं तो हमें विद्युत् आघात (electric shock) क्यों नहीं लगता? (घर को लोहे का पिंजरा (steel cage) मान लीजिए; अत: उसके अन्दर कोई विद्युत् - क्षेत्र नहीं है।)
(b) एक व्यक्ति शाम के समय अपने घर के बाहर 2m ऊँचा अवरोधी पट्ट (insulating slab) रखता है जिसके शिखर पर 1m² क्षेत्रफल की बड़ी ऐल्युमिनियम की चादर (sheet) है। अगली सुबह वह यदि धातु की चादर को छूता (touch) है तो क्या उसे विद्युत् आघात लगेगा?
(c) वायु की थोड़ी - सी चालकता के कारण सारे संसार में औसतन वायुमण्डल में विसर्जन धारा (discharging eurrent) 1800 A मानी जाती है। इस स्थिति में यथासमय (in due course) वातावरण स्वयं पूर्णतः निरावेशित होकर विद्युत् उदासीन (neutral) क्यों नहीं हो जाता? दूसरे शब्दों में, वातावरण (atmosphere) को कौन आवेशित रखता है?
(d) तड़ित (lightining) के दौरान वातावरण की विद्युत् ऊर्जा, ऊर्जा के किन रूपों में क्षयित होती है?
[संकेत: पृष्ठ आवेश घनत्व = 10^-9 Cm^-2 के अनुरूप पृथ्वी के (पृष्ठ) पर नीचे की दिशा में लगभग 100Vm^-1 का विद्युत क्षेत्र होता है। लगभग 50 km ऊंचाई तक (जिसके बाहर यह अच्छा चालक है) वातावरण की थोड़ी सी चालकता के कारण लगभग + 1800C  का आवेश प्रति सेकंड समग्र रूप से पृथ्वी में पंप होता रहता है। तथापि, पृथ्वी निरावेशित नहीं होती, क्योंकि संसार में हर समय लगातार तड़ित तथा तड़ित-झंझा होती रहती है जो समान मात्रा में ऋणावेश पृथ्वी में पंप कर देती है।]
हल: 
(a) हमारे शरीर एवं पृथ्वी दोनों के विभव समान होने के कारण शरीर से होकर कोई विद्युत् धारा प्रवाहित नहीं होती, इसीलिए हमें विद्युत् आघात नहीं लगता है।
(b) हाँ, पृथ्वी तथा ऐल्युमिनियम की चादर मिलकर एक संधारित्र बनाते हैं जिसमें परावैद्युत का कार्य अवरोधी पट्टिका (insulating slab) करती है। वायुमण्डलीय आवेश के लगातार गिरते रहने से अर्थात् वायुमण्डल में अपरिवर्तित विसर्जन धारा धीरे-धीरे ऐल्युमिनियम की चादर को आवेशित कर देती है जिससे यह उच्च विभव प्राप्त कर लेती है, अतः व्यक्ति जब इस चादर को छूता है तो उसके शरीर से होकर एक विद्युत् धारा प्रवाहित होती है। इसी कारण आघात का अनुभव (feeling) होता है।
(c) यद्यपि वायुमण्डल 1800 A की औसत विसर्जन धारा के कारण लगातार निरावेशित होता रहता है, परन्तु साथ ही यह तड़ित तथा झंझावात (thunder) के कारण लगातार आवेशित भी होता रहता है और इन दोनों के बीच एक सन्तुलन बना रहता है जिससे कि वायुमण्डल कभी भी पूर्णत: निरावेशित नहीं हो पाता।
(d) तड़ित के दौरान वातावरण की विद्युत् ऊर्जा, प्रकाश ऊर्जा, ध्वनि ऊर्जा तथा ऊष्मीय ऊर्जा के रूप में क्षयित (decay) होती है।