RBSE Solutions for Class 12 Physics Chapter 14 अर्द्धचालक इलेक्ट्रॉनिकी-पदार्थ, युक्तियाँ तथा सरल परिपथ

Rajasthan Board RBSE Solutions for Class 12 Physics Chapter 14 अर्द्धचालक इलेक्ट्रॉनिकी-पदार्थ, युक्तियाँ तथा सरल परिपथ Textbook Exercise Questions and Answers.

RBSE Class 12 Physics Solutions Chapter 14 अर्द्धचालक इलेक्ट्रॉनिकी-पदार्थ, युक्तियाँ तथा सरल परिपथ

RBSE Class 12 Physics अर्द्धचालक इलेक्ट्रॉनिकी-पदार्थ, युक्तियाँ तथा सरल परिपथ Textbook Questions and Answers

प्रश्न 1. 
n - प्रकार के सिलिकॉन के लिए निम्न में कौन - सा कथन सत्य है?
(a) इलेक्ट्रॉन बहुसंख्यक वाहक (majority carriers) हैं और त्रिसंयोजी परमाणु अपमिश्रक (dopants) हैं।
(b) इलेक्ट्रॉन अल्पसंख्यक वाहक (minority earriers) हैं और पंचसंयोजी (pentavalent) परमाणु अपमिश्रक हैं।
(c) कोटर अल्पसंख्यक वाहक हैं और पंचसंयोजी परमाणु अपमिश्रक हैं।
(d) कोटर बहुसंख्यक वाहक हैं और त्रिसंयोजी परमाणु अपमिश्रक हैं।
उत्तर:
(c), संकेत: शुद्ध अर्द्धचालक में पंचसंयोजी अशुद्धि मिलाने पर-प्रकार का अर्द्धचालक प्राप्त होता है। इसमें इलेक्ट्रॉन बहुसंख्यक और होल अल्पसंख्यक आवेश वाहक होता है।

प्रश्न 2. 
प्रश्न 1 में p - प्रकार के अद्धंचालक के लिए कौन - सा कथन सत्य होगा?
उत्तर:
(d), संकेत: शुद्ध अर्द्धचालक में त्रिसंयोजी अशुद्धि मिलाने पर p - प्रकार का अर्द्धचालक प्राप्त होता है और इसमें होल बहुसंख्यक आवेश वाहक तथा इलेक्ट्रॉन अल्पसंख्यक आवेश वाहक होते हैं।

प्रश्न 3. 
कार्बन, सिलिकॉन तथा जर्मेनियम, प्रत्येक में चार संयोजक. इलेक्ट्रॉन हैं। इनकी विशेषता संयोजन तथा चालन बैण्ड के ऊर्जा अन्तराल अथवा बैण्ड अन्तराल द्वारा अभिलेखित (characterised) की गई है जो क्रमशः (E_g)_C, (E_g)_Si तथा (E_g)_Ge के बराबर है।
निम्नलिखित में से कौन - सा कथन सत्य है-
(a) (E_g)_Si < (E_g)_Ge < (E_g)_C
(b) (E_g)_C < (E_g)_Ge > (E_g)_Si
(c) (E_g)_C > (E_g)_Si > (E_g)_Ge
(d) (E_g)_C = (E_g)_Si = (E_g)_Ge
उत्तर:
कथन (c), सही है। संकेत: चालन बैण्ड तथा संयोजकता बैण्ड के बीच ऊर्जा अन्तराल कार्बन के लिए सबसे अधिक, सिलिकॉन के लिए उससे कम तथा जर्मेनियम के लिए सबसे कम होता है।

प्रश्न 4.
बिना बायस (unbiased) p - n सन्धि में, होल p - क्षेत्र से n - क्षेत्र की ओर विसरित (diffuse) होते हैं, क्योंकि
(a) n - क्षेत्र में मुक्त इलेक्ट्रॉन उन्हें आकर्षित करते हैं। 
(b) ये विभवान्तर के कारण सन्धि के पार गति करते हैं। 
(c) p - क्षेत्र में होल सान्द्रता, n - क्षेत्र में उनकी सान्द्रता से अधिक है। 
(d) उपर्युक्त सभी।
उत्तर:
कथन (c) सही है। संकेत: विसरण की घटना सान्द्रता प्रवणता के कारण होती है, n - क्षेत्र की अपेक्षा, p - क्षेत्र में कोटरों की सान्द्रता अधिक होती है। इसीलिए कोटरों का विसरण p - क्षेत्र से n - क्षेत्र की ओर अधिक होता है।

प्रश्न 5.
जब p - n सन्धि पर अग्न अभिनति लगायी जाती है तो यह
(a) विभव प्राचीर बढ़ाती है। 
(b) बहुसंख्यक आवेश धारा को शुन्य कर देती है। 
(c) विभव प्राचीर को कम कर देती है। 
(d) उपर्युक्त में से कोई नहीं।
उत्तर:
(c), संकेत: अग्र अभिनति विभव प्राचीर का विरोध करती है, अतः विभव प्राचीर कम हो जाता है। जब अन अभिनति का मान विभव प्राचीर के बराबर अथवा अधिक हो जाता है, तो विभव प्राचीर लुप्त हो जाता है तथा अन धारा बहने लगती है।

प्रश्न 6. 
अर्द्ध तरंग दिष्टकारी में यदि निवेशी आवृत्ति 50Hz हो, तो निर्गत आवृत्ति कितनी होगी? इसी निवेशी आवृत्ति के लिए पूर्ण तरंग दिष्टकारी की निर्गत आवृत्ति कितनी होगी?
उत्तर:
अर्द्ध तरंग दिष्टकारी में निर्गत आवृत्ति निवेशी आवृत्ति के बराबर होती है क्योंकि प्रत्येक निवेशी चक्र के संगत एक बार ही निर्गत मिलता है। अत: अर्द्ध तरंग दिष्टकारी के निर्गत की आवृत्ति = 50 Hz.
पूर्ण तरंग दिष्टकारी में निवेशी के एक चक्र में दो बार निर्गत वोल्टता मिलती है अतः निर्गत आवृत्ति
= 2 x निवेशी आवृत्ति = 2 x 50 = 100 Hz. 

प्रश्न 7.
एक p - n फोटो डायोड 2.8 eV बैण्ड अन्तराल वाले अर्द्ध चालक पदार्थ से बनाया गया है। क्या यह 6000 nm की तरंगदैर्ध्य को संसूचित कर सकता है?
उत्तर:
6000 nm = 6000 x 10^-9 = 6 x 10^-6 m 
∴ फोटॉन की ऊर्जा
E = \(\frac{h c}{\lambda}=\frac{6 \cdot 6 \times 10^{-34} \times 3 \times 10^8}{6 \times 10^{-6}}\)
= 3.3 x 10^-20 J
∴ E = \(\frac{3.3 \times 10^{-20}}{1 \cdot 6 \times 10^{-19}}\) = 0.2 eV
यह फोटॉन ऊर्जा (0.2 eV) बैण्ड अन्तराल (2.8 eV) से काफी कम है, अत: फोटो डायोड दी गई तरंगदैर्ध्य को संसूचित नहीं कर सकता।

प्रश्न 8. 
सिलिकॉन परमाणुओं की संख्या 5 x 10²⁸ m^-3 है। इसे आर्सेनिक के 5 x 10²² परमाणु प्रति m³ से तथा इण्डियम के 5 x 10²⁰ परमाणु प्रति m3 से एक साथ अपमिश्रित किया जाता है। इलेक्ट्रॉनों तथा कोटरों की संख्या ज्ञात कीजिए। दिया है: n_i = 1.5 x 10¹⁶ m^-3. यह भी बताइए कि दिया गया पदार्थ n - टाइप है या p - टाइप।
उत्तर:
आर्सेनिक दाता प्रकार (Donor type) की अशुद्धि है और इण्डियम ग्राही प्रकार (Acceptor type) की अशुद्धि है। अत: इलेक्ट्रॉनों की संख्या
n_e = n_D - n_A = 5 x 10²² = 5 x 10²⁰
= 4.95 x 10²² m^-3
हम जानते है। कि
n_i² = n_e x n_h
∴ n_h = \(\frac{n_i^2}{n_e}=\frac{\left(1.5 \times 10^{16}\right)^2}{4.95 \times 10^{22}}\)
= 4.54 x 10⁹ m
∵ n_e > n_h
अत: दिया गया पदार्थ n - प्रकार का अर्द्ध चालक है।

प्रश्न 9.
किसी नैज अर्द्धचालक में ऊर्जा अन्तराल E_g का मान 1.2 eV है। इसकी कोटर गतिशीलता, इलेक्ट्रॉन गतिशीलता से बहुत कम हैतथा ताप पर निर्भर नहीं करती। इसकी 600 K ताप तथा 300 K ताप पर चालकताओं का अनुपात क्या है? मान लीजिए कि नैज आवेश वाहकों की सान्दता (n_i) की ताप निर्भरता निम्न सूत्र से दी जाती है-
n_i = n₀ exp.\(\left(-\frac{\mathbf{E}_g}{2 k_{\mathbf{B}} \mathrm{T}}\right)\)
जिसमें n₀ एक नियतांक है, 
हल: 
दिया है: E_g = 1.2 eV, T₁ = 600 K, T₂ = 300K
∵ अर्द्ध चालक में कोटर गतिशीलता, इलेक्ट्रॉन गतिशीलता की तुलना में बहुत कम है, अत: अर्द्धचालक की चालकता केवल इलेक्ट्रॉनों के कारण है।
∴ चालकता, σ = en_eµ_e, जहाँ n_e = इलेक्ट्रॉन सान्द्रता 
या σ ∝n_e
अतः \(\frac{\sigma_1}{\sigma_2}=\frac{n_1}{n_2}=\frac{n_0 e^{-\mathrm{E}_g / 2 k_{\mathrm{B}} \mathrm{T}_1}}{n_0 e^{-\mathrm{E}_g / 2 k_{\mathrm{B}} \mathrm{T}_2}}\)

प्रश्न 10.
एक p - n सन्धि डायोड में धारा 'I' निम्न प्रकार प्रदर्शित की जाती है-
I = I₀ exp\(\left[\frac{e \mathrm{~V}}{k_{\mathrm{B}} \mathrm{T}}-1\right]\) 
जिसमें I₀ उत्क्रम संतृप्त धारा है, V डायोड के आर - पार वोल्टेज है जो अग्र अभिनति के लिए धनात्मक तथा उत्तम अभिनति के लिए ऋणात्मक है, kB = 8.6 x 10^-5 eVK^-1 बोल्ट्ज मैन नियतांक है, T परम ताप K (केल्विन) में है। यदि एक दिये गये डायोड के लिए I0 = 5 x 10^-12 A तथा T = 300, तो
(a)0.6 V के अग्र वोल्टेज के बीच अग्र धारा कितनी है?
(b) यदि डायोड के सिरों के बीच अग्र वोल्टेज 0.7 Vतक बड़ा दिया जाये, तो धारा में वृद्धि कितनी होगी?
(c) गतिक प्रतिरोध कितना है?
(d) यदि उत्क्रम अभिनति वोल्टेज 1 V से 2 V कर दिया जाये, तो धारा में परिवर्तन कितना होगा?
हुल: 
(a) सन्धि डायोड में धारा,
I = I₀ exp\(\left[\frac{e \mathrm{~V}}{k_{\mathrm{B}} \mathrm{T}}-1\right] \)
दिया है: V = 0.6 volt, T = 300K, I₀ = 5 x 10^-12 A 
k_B = 8.6 x 10^-5 eVK^-1
= 8.6 x 10^-5 eVK^-1
= 8.6 x 10^-5 x 1.6 x 10^-19 JK^-1
(a) जब V = 0.6 V

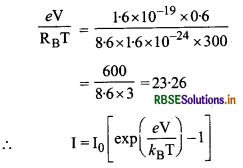
= 5 x 10^-12 [exp (23.26) - 1] A
= 5 x 10^-12[1.2586 x 10¹⁰ - 1] A 
= 5 x 10^-12 x 1.2586 x 10¹⁰ A
= 0.06293 A 

(b) जब V = 0.7 V

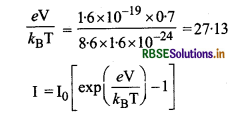
= 5 x 10^-12 [exp (27.13) - 1] A 
= 5 x 10^-12 [6.07 x 10¹¹ - 1] A
= 5 x 10^-12 x 6.07 x 10¹¹ A = 3.035 A 
धारा में वृद्धि ∆I = 3.035 - 0.06293 = 2.972 A 

(c) ∆V = 0.7 - 0.6 = 0.1 V, ∆I = 2.972A
गतिक प्रतिरोध
r_d = \(\frac{\Delta \mathrm{V}}{\Delta \mathrm{I}}=\frac{0.1}{2.972}\) = 0.0336 Ω

(d) दोनों वोल्टताओं के लिए धारा I का मान लगभग I0 के समान होगा, इससे ज्ञात होता है कि उत्क्रम अभिनति में गतिक प्रतिरोध का मान अनन्त होगा।

प्रश्न 11. 
आपको चित्र (a) व (b) में प्रदर्शित दो परिपथ दिये गये हैं। दर्शाइए कि परिपथ (a) OR गेट की भाँति और परिपथ (b) AND गेट की भाँति कार्य करता है।

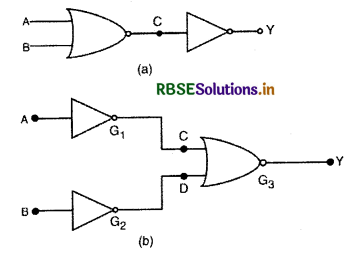
हल: 
(a) पहला गेट NOR गेट है, अत: इसका निर्गत
C = \(\overline{\mathrm{A}+\mathrm{B}}\)
दूसरा गेट NOT गेट है जिसके निवेशी से निर्गत C जोड़ा गया है। अत: संयोजन का निर्गत
Y = \(\overline{\mathrm{C}}=(\overline{\mathrm{A}+\mathrm{B}})=(\mathrm{A}+\mathrm{B})\)
या Y = A + B = A OR B
यह OR गेट का बूलियन व्यंजक है अत: चित्र (a) में प्रदर्शित परिपथ OR गेट के तुल्य है।

(b) चित्र (b) में प्रदर्शित 
NOT गेट G₁ का निर्गत C = \(\overline{\mathrm{A}}\)
NOT गेट G₂ का निर्गत D = \(\overline{\mathrm{B}} \)
गेट G₃, NOR गेट है जिसके निवेशी C व D हैं।
∴ G₃ का निर्गत Y = \(\overline{\mathrm{C}+\mathrm{D}}=\overline{\overline{\mathrm{A}}+\overline{\mathrm{B}}}\)
= \(\bar{A} \cdot \bar{B}\) (डी - मॉर्गन के नियम से) 
या Y = A.B = A AND B 
स्पष्ट है कि संयोजन (b) AND गेट की भांति व्यवहार करता है।

प्रश्न 12.
चित्र में जुड़े NAND गेट की सत्यता सारणी लिखिए। इस परिपथ द्वारा कृत सही तर्क क्रिया (exact logic operation) को पहचानिए।

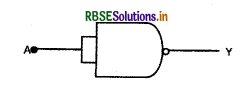
उत्तर:
चित्र में प्रदर्शित गेट एक NAND गेट है जिसके दोनों निवेशों को लघुपचित (short circuit) करके एक कर दिया गया है।
AND गेट का निर्गत Y' = A.A = A 
∴ NAND गेट का निर्गत Y = \(\overline{\mathrm{Y}^{\prime}}=\overline{\mathrm{A}}\)

स्पष्ट है दिये गये परिपथ की तर्क क्रिया NOT गेट की है।

प्रश्न 13. 
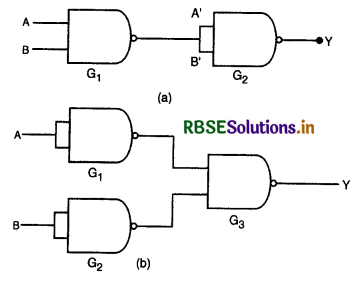
आपको दो परिपथ चित्र (a) व (b) दिये गये हैं, जिनमें NAND गेट (gates) हैं। इन परिपथों द्वारा की गयी तर्क - क्रियाओं को पहचानिए।

हल: 
परिपथ (a): NAND गेट के निवेशी A व B है।
∴ गेट G₁ का निर्गत, C = \(\overline{\mathrm{A} \cdot \mathrm{B}}=\overline{\mathrm{A}}+\overline{\mathrm{B}}\) (डी - मोर्गन नियम से) 
गेट G₂ के निवेशी A' = \((\overline{\mathrm{A}}+\overline{\mathrm{B}})\) और B = \((\overline{\mathrm{A}}+\overline{\mathrm{B}})\)
∵ गेट G₂ भी NAND गेट है, इसलिए G₂ का निर्गत
Y= \(\overline{\mathrm{A}^{\prime} \cdot \mathrm{B}^{\prime}}=(\overline{\overline{\mathrm{A}}+\overline{\mathrm{B}}}) \cdot(\overline{\mathrm{A}}+\overline{\mathrm{B}})\)
= \((\overline{\overline{\mathrm{A}}+\overline{\mathrm{B}}})\)
या Y = \(\overline{\bar{A} \cdot \mathrm{B}}\) = A.B 
या Y = A.B = A AND B
यह AND गेट को तर्क क्रिया है, अत: परिपथ (a) AND गेट की भाँति कार्य करता है।
परिपथ (b): गेट G₁ का निर्गत y₁ और G₂ का निर्गत y₂ है और ये दोनों गेट NAND गेट है। अतः
y₁ = \(\overline{\mathrm{A} \cdot \mathrm{A}}=\overline{\mathrm{A}}\) और y₂ = \(\overline{\mathrm{B} \cdot \mathrm{B}}=\overline{\mathrm{B}}\)
∵ अन्तिम गेट, (जो कि NAND गेट है) के निवेशीव है अतः अन्तिम निर्गत
Y = \(\overline{y_1 \cdot y_2}=\overline{y_1}+\overline{y_2}\) (डी - मॉर्गन नियम से)
= \(\overline{\bar{A}+\bar{B}}\)
या Y = A + B = A OR B
यही इस परिपथ की तर्क संक्रिया है। स्पष्ट है कि पूरा परिपथ (b) OR गेट की भांति व्यवहार करता है।

प्रश्न 14. 
चित्र में दिये गये NOR गेट युक्त परिपथ की सत्यता सारणी लिखिए और इस परिपथ द्वारा अनुपालित तर्क संक्रियाओं (OR, AND, NOT) को अभिनिर्धारित कीजिए।

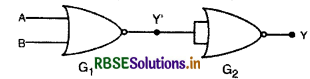
(संकेत - A = 0, B = 1 तब दूसरे NOR गेट के निवेश A और B, 0 होंगे और इस प्रकार Y = 1 होगा। इसी प्रकार A और B के दूसरे संयोजनों के लिए के मान प्राप्त कीजिए। OR, AND, NOT गेटों की सत्यता सारणी से तुलना कीजिए और सही विकल्प प्राप्त कीजिए।) 
हल: 
गेट G₁ के लिए बूलियन व्यंजक
Y' = \(\overline{\mathrm{A}+\mathrm{B}}=\overline{\mathrm{A} \cdot \mathrm{B}}\)
यही निर्गत Y' गेट G₂ का निवेशी है अत: अन्तिम निर्गत
Y = \(\overline{\mathrm{Y}^{\prime}}=\overline{\overline{\mathrm{A}} \cdot \overline{\mathrm{B}}}=\overline{\mathrm{A}}+\overline{\mathrm{B}}\) = A + B 
या Y = A OR B
स्पष्ट है कि पूरा संयोजन OR गेट के तुल्य है। सत्यता सारणी नीचे दी जा रही है-

प्रश्न 15.
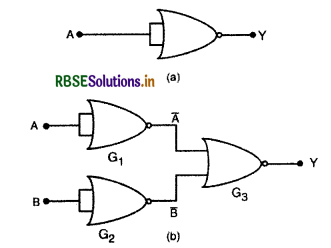
चित्र (a) व (b) में प्रदर्शित परिपथों में केवल NOR गेट लगे हैं। इन परिपथों की सत्यता सारणी लिखिए तथा इनके द्वारा की गई तर्क क्रियाओं (OR, AND, NOT) को पहचानिए।

हल: 
परिपथ (a): दिया गया परिपथ NOR गेट है जिसके दोनों निवेशी लघुपथित कर दिये गये हैं। 
इस परिपथ का निर्गम निम्नलिखित होगा-
Y = \(\overline{\mathrm{A}}\)
सत्यता सारणी-

यह NOT गेट की तर्क संक्रिया है अत: चित्र (a) में प्रदर्शित गेट NOT गेट है।
परिपथ (b): NOR गेट G₁ का निर्गत A' = \(\overline{\mathrm{A}}\)
NOR गेट G₂ का निर्गत B' = \(\overline{\mathrm{A}}\)
ये ही दोनों निर्गत A' व B' तीसरे गेट G₂ के निवेशी हैं अत: अन्तिम निर्गत
Y = \(\overline{\mathrm{A}^{\prime}+\mathrm{B}^{\prime}}=\overline{\overline{\mathrm{A}}+\overline{\mathrm{B}}}=\overline{\mathrm{A} \cdot \mathrm{B}}\) (डी - मॉर्गन नियम से)
या Y = A.B = A AND B 
स्पष्ट है कि पूरा परिपथ (b) AND गेट के तुल्य है।
सत्यता सारणी