RBSE Solutions for Class 12 Physics Chapter 13 नाभिक

Rajasthan Board RBSE Solutions for Class 12 Physics Chapter 13 नाभिक Textbook Exercise Questions and Answers.

RBSE Class 12 Physics Solutions Chapter 13 नाभिक

RBSE Class 12 Physics नाभिक Textbook Questions and Answers

प्रश्न 1. 
(a) लीथियम के दो स्थायी समस्थानिकों 3LI6 एवं 3Li7 की बहुलता (abundances) का प्रतिशत क्रमशः 7.5 एवं 92.5 है। इन समस्थानिकों के द्रव्यमान क्रमशः 6.01512 u एवं 7.01600 u है। लीथियम का परमाणु द्रव्यमान ज्ञात कीजिए।
(b) बोरॉन के दो स्थायी समस्थानिक ₅B¹⁰ एवं ₅B¹¹ हैं। उनके द्रव्यमान क्रमश: 10.01294u एवं 11.00931 u एवं बोरॉन का परमाणु भार 10.811 u है। ₅B¹⁰ एवं ₅B¹¹ की बहुलता ज्ञात कीजिए। 
उत्तर:
(a) समस्थानिकों के द्रव्यमान-
m₁ = 6.01512 u, m₂ = 7.01600 u
समस्थानिकों की बहुलताओं का प्रतिशत 
P₁ = 7.5%; P₂ = 92.5% 
औसत परमाणु द्रव्यमान
\(\mathbf{M}=\frac{\mathrm{P}_1 m_1+\mathrm{P}_2 m_2}{\mathrm{P}_1+\mathrm{P}_2}\)
M = \(\frac{7.5 \times 6.01512+92.5 \times 7.01600}{7.5+92.5}\)
या M = 6.9414 u

(b) यदि ₅B¹⁰  व ₅B¹¹ की प्रतिशत बहुलताएँ क्रमशः P₁ व P₂ हों तो औसत परमाणु द्रव्यमान
\(\mathbf{M}=\frac{m_1 \mathrm{P}_1+m_2 \mathrm{P}_2}{\mathrm{P}_1+\mathrm{P}_2}\)
या \(10 \cdot 811=\frac{10.01294 \times \mathrm{P}_1+11.00931 \times \mathrm{P}_2}{\mathrm{P}_1+\mathrm{P}_2}\)
या 10.811 = \(\frac{10.01294 \mathrm{P}_1+11.00931 \times \mathrm{P}_2}{100}\)
या 10.01294 P₁ + 11.00931 P₂ = 1081.1
∵ P₁ + P₂ = 100
∴ P₂ = (100 - P₁) रखकर हल करने पर 
P₁ = 19.9% और P₂ = 100 - P₁ = 100 - 19.9 = 80.1%

प्रश्न 2. 
नियोंन के तीन स्थायी (stable) समस्थानिकों की बहुलता क्रमश: 90.51%, 0.27% व 9.22% है। इन समस्थानिकों के परमाणु द्रव्यमान क्रमश: 19.99 u, 20.99 u  व 21.99 u हैं। नियॉन का औसत परमाणु द्रव्यमान ज्ञात कीजिए। 
उत्तर:
नियॉन का औसत परमाणु द्रव्यमान
\(\mathrm{M}_{\mathrm{av}}=\frac{m_1 \mathrm{P}_1+m_2 \mathrm{P}_2+m_3 \mathrm{P}_3}{\mathrm{P}_1+\mathrm{P}_2+\mathrm{P}_3}\)
दिया है: P₁ = 90.51%, P₂ = 0.27%, P₃ = 9.22%
और m₁ = 19.99 u, m₂ = 20.99 u, m₃ = 21.99 u
∴ \(\mathrm{M}_{\mathrm{av}}=\frac{19.99+90.51+20.99 \times 0.27+21.99 \times 9.22}{90.51+0.27+9.22}\)
\(=\frac{1809.29 \times 567+202.75}{100}\)
या M_av = 20.18 u

प्रश्न 3.
नाइट्रोजन नाभिक (₇N¹⁴) की बन्धन ऊर्जा MeV में ज्ञात कीजिए। m_N = 14.00307 u
उत्तर:
दिया है: m_N = 14.00307 u; m_p = 1.00783 u; m_n = 1.00867 u
∴ ₇N¹⁴ का सम्भावित द्रव्यमान
m_c = [Z.mp + (A - Z) m_n]
= [7 x 1.00783 + 7 x 1.00877] u
= 14.1155 u
∴ द्रव्यमान क्षति
∆m = m_c - m_a
= (14.11550 - 14.00307) u
= 0.11243 u
∵ 1 u = 931 MeV
∴ ₇N¹⁴ नाभिक की बन्धन ऊर्जा
∆E = ∆m (amu में) x 931 MeV
= 0.11243 x 931 MeV
= 104.67 MeV
≈ 104.7 MeV

प्रश्न 4.
निम्नलिखित आँकड़ों के आधार पर ₂₆Fe⁵⁶ एवं ₈₃Bi²⁰⁹ नाभिकों की बन्धन ऊर्जा प्रति न्यूक्लियॉन (Mev में) ज्ञात कीजिए। ₂₆Fe⁵⁶ का द्रव्यमान = 55.934939 u; ₈₃Bi²⁰⁹ का द्रव्यमान 208.980388 u
हल: 
दिया है: m_p = 1.007825 u; m_n = 1.008665 u; 
(i) m_Fe = 55.934939 u
इस नाभिक (₂₆F⁵⁶) में प्रोटॉनों की संख्या Z = 26 और न्यूटॉनों की संख्या (A - Z) = 56 - 26 = 30
∴ संभावित द्रव्यमान 
m_c = [Z.m_p + (A - Z) m_n]
= [26 x 1.007825 + 30 x 1.008665] u
= (26.20345 + 30.25995) u
= 56.4634 u
∴ द्रव्यमान क्षति
∆m = m_c - m_a
या ∆m = (56.4634 - 55.934939) u
= 0.528461 u
∴ 26Fe56 नाभिक की बन्धन कर्जा 
∆E = ∆m x 931 MeV
= 0.528461 x 931 = 492.26 MeV
अत: ₂₆Fe⁵⁶ की बन्धन ऊर्जा प्रति न्यूक्लिऑन = \(\frac{\Delta \mathrm{E}}{\mathrm{A}}\)
\(=\frac{492 \cdot 26}{56} \mathrm{MeV}\)
= 8.79 MeV

(ii) इसी प्रकार ₈₃Bi²⁰⁹ के लिए
m_Bi = 208.980388 u
Z = 83; (A-Z) = (209 - 83) = 126
∴ m_C = Z.m_p + (A - Z) m_n
= (83 x 1.007825 + 126 x 1.008665) u
= (83.649475 + 127.091790) u
= 210.741260 u
∴ ∆m = m_c - m_a
= (210.741260 - 208.980388) u
या ∆m = 1.760872 u
∴ ∆E = 1.760872 x 931 MeV
अत:बन्धन ऊर्जा प्रति न्यूक्लिऑन
\(=\frac{\Delta \mathrm{E}}{\mathrm{A}}=\frac{1.760872 \times 931 \mathrm{MeV}}{209}\)
= 7.84 MeV

प्रश्न 5. 
एक दिये गये सिक्के (coin) का द्रव्यमान 3.0 g है। उस ऊर्जा की गणना कीजिए जो इस सिक्के के सभी न्यूट्रॉनों एवं प्रोटॉनों को एक - दूसरे से अलग करने के लिए आवश्यक हो। सरलता के लिए मान लीजिए कि सिक्का पूर्णतः (entirely) ₂₉Cu⁶³ परमाणुओं का बना है। ₂₉C⁶³ का द्रव्यमान = 62.92960 है।
उत्तर:
दिया है-
₂₉Cu⁶³ का द्रव्यमान m = 62.92960 u 
₂₉Cu⁶³ का ग्राम परमाणु द्रव्यमान = 63 g
न्यूट्रॉन का द्रव्यमान m_n = 1.008665 u 
प्रोटॉन का द्रव्यमान m_p = 1.007825 u
∵63 g ताँबे में परमाणुओं की संख्या
= N = 6.02 x 10²³ 
∴ 3g ताँबे में परमाणुओं की संख्या
n = \(\frac{6.02 \times 10^{23} \times 3}{63}\)
n = 2.868 x 10²²
₂₉Cu⁶³ के एक परमाणु में प्रोटॉनों की संख्या Z = 29 
और ₂₉Cu⁶³ के एक परमाणु में न्यूट्रॉनों की संख्या
= (A - Z) = 63 - 29 = 34 
तौबे के एक नाभिक के न्यूक्लियानों का द्रव्यमान
= Zm_p + (A - Z) m_n
= (29 x 1.007825 + 34 x 1.008665) u
= (29.226925 + 34.294610) u
= 63.521535 u
∴ एक नाभिक की द्रव्यमान क्षति
= 63.521535 - 62.9260
= 0.595535 u
∴ 3 g ताँबे के लिए कुल द्रव्यमान क्षति
∆m = n x एक नाभिक के लिए द्रव्यमान क्षति
= 2.868 x 10²² x 0.595535 u
= 1.70 x 10²² u
∴3g कॉपर की बन्धन ऊर्जा
∆E = ∆m(u) x 931 MeV
= 1.70 x 10²² x 931 MeV
= 1583.5 x 10²² MeV
= 1.584 x 10²⁵ MeV
= 1.584 x 10²⁵ x 1.6 x 10^-13 J
= 2.535 x 10¹² J
अत: 3g कॉपर के समस्त न्यूक्लिऑनों को अलग - अलग करने के लिए आवश्यक ऊर्जा = 1.584 x 10²⁵ MeV = 2.535 x 10¹² J

प्रश्न 6. 
निम्नलिखित के लिए नाभिकीय समीकरण लिखिए

उत्तर:

प्रश्न 7.
एक रेडियोएक्टिव समस्थानिक की अर्द्ध - आयु T वर्ष है। कितने समय के बाद इसकी एक्टिवता (activity) प्रारम्भिक एक्टिवता की (a) 3.125% (b) 1% रह जायेगी?
उत्तर:
(a) सक्रियता का मान n अर्द्ध आयुओं के बाद

∴ n = 5
अत: अभीष्ट समय t = nT = 5T 

(b) इस प्रश्न में R = \(\frac{\mathrm{R}_0}{100}\)

या t = 6.65 T

प्रश्न 8. 
जीवित कार्बन युक्त द्रव्य (living carbon containing matter) की सामान्य एक्टिवता (normal activity), प्रति ग्राम कार्बन के लिए 15 क्षय प्रति मिनट है। यह एक्टिवता, स्थायी समस्थानिक ₆C¹² के साथ - साथ अल्प मात्रा (small proportion) में विद्यमान रेडियोएक्टिव कार्बन, ₆C¹⁴ के कारण होती है। जीव (organism) की मृत्यु होने पर वायुमण्डल के साथ इसकी अन्योन्य क्रिया (interaction) (जो उपयुक्त संतुलित एक्टिवता को बनाये रखती है। समाप्त हो जाती है तथा इसकी एक्टिवता कम होनी शुरू हो जाती है। ₆C¹⁴ की अर्द्ध - आयु(5730 वर्ष) और नमूने (specimen) की मापी गई एक्टिवता के आधार पर इसकी सन्निकट आयु की गणना की जा सकती है। यही पुरातत्व विज्ञान में प्रयुक्त होने वाली ₆C¹⁴ काल निर्धारण (carbon dating) पद्धति का सिद्धान्त है। यह मानकर कि मोहनजोदड़ो से प्राप्त किसी नमूने की एक्टिवता क्षय प्रति मिनट प्रति ग्राम कार्बन है। सिन्धु घाटी सभ्यता की सन्निकट आयु (approximate age) का आंकलन कीजिए।
हल: 
दिया है- R₀ = 15 क्षय प्रति मिनट; R= 9 क्षय प्रति मिनट, T = 5730 वर्ष; t = ?
∵ R = R₀ e^-λt
∴ 9 = 15 e^-λt

=4224 वर्ष

प्रश्न 9.
8.0 mCi सक्रियता का रेडियोएक्टिव स्त्रोत प्राप्त करने के लिए ₂₇C⁶⁰ की कितनी मात्रा की आवश्यकता होगी? ₂₇C⁶⁰ की अद्ध - आयु 5.3 वर्ष है।
हल: 
दिया है- सक्रियता R= 8.0 mCi = 8.0 x 10^-3 x 3.7 x 10¹⁰ विघटन/सेकण्ड
= 29.6 x 10⁷ विघटन/सेकण्ड 
अर्द्ध - आयु T = 5.3 वर्ष = 5.3 x 365 x 3600 सेकण्ड

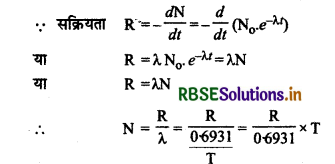
∴ आवश्यक परमाणुओं की संख्या 
या N = \(\frac{\left(29.6 \times 10^7\right) \times(5.3 \times 365 \times 3600)}{0.6931}\)
N = 7.15 x 10¹⁶ परमाणु 
∵ ₂₇Co⁶⁰ का ग्राम परमाणु द्रव्यमान = 60g 
अर्थात् (NA) 6.02 x 10²³ परमाणुओं का द्रव्यमान = 60g
∴ 7.133 x 10¹⁶ परमाणुओं का द्रव्यमान
= \(\frac{60}{6.02 \times 10^{23}} \times 7 \cdot 15 \times 10^{16}\)
= 7.123 x 10^-6 g

प्रश्न 10. 
₃₈Sr⁹⁰ की अर्द्ध आयु 28 वर्ष है। इस समस्थानिक के 15 mg की विघटन दर (disintegration rate) क्या है?
उत्तर:
दिया है: पदार्थ का द्रव्यमान = 15 x 10^-3 g.
अर्द्ध आयु T = 28 वर्ष = 28 x 3.154 x 10 s
15 x 10^-3 स्ट्राँशियम (Sr - 90) में परमाणुओं की संख्या 

प्रश्न 11.
सोने के समस्थानिक ₇₉Au¹⁹⁷ तथा चाँदी के समस्थानिक ₄₇Ag¹⁰⁷ की त्रिज्याओं का सन्निकट (approximate) अनुपात जात कीजिए। 
उत्तर:
दिया है:
A₁ = 197; A₂ = 107
\(\frac{\mathrm{R}_{\mathrm{Au}}}{\mathrm{R}_{\mathrm{Ag}}}=\frac{\mathrm{R}_1}{\mathrm{R}_2}=?\)
∵ नाभिक की त्रिज्या R = R₀ (A)^1/3

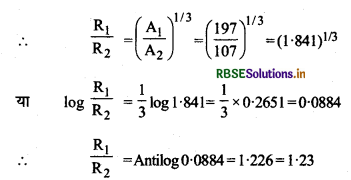
या R₁ : R₂ = 1.23 : 1

प्रश्न 12.
(a) ⁸⁸Ra²²⁶ एवं (b) ₈₆Rn²²⁰ नाभिकों के α - क्षय में उत्सर्जित α - कणों का Q - मान एवं गतिज ऊर्जा ज्ञात कीजिए।
दिया है: m(₈₈Ra²²⁶) = 226.02540 u; m(₈₆Rn²²²) = 222.01750 u; m(₈₆R²²⁰) = 220.01137 u; m(₈₄Po²¹⁶) = 216.00180 u 
उत्तर:
(a) ₈₈Ra²²⁶ नाभिक से α - क्षय की अभिक्रिया
₈₈Ra²²⁶ → ₈₆Rn²²² + ₂He⁴ + Q(ऊर्जा) 
समी. के L.H.S. का द्रव्यमान
m_i = 226.02540 u
समी. के R.H.S. का द्रव्यमान
m_f = (222.01750 + 4.002603) u
क्योंकि m_α = 4.002603 u
∴ m_f = 226.020103 u
∴ द्रव्यमान क्षति ∆m = m_i - m_f
= (226.02540 - 226.020103) u
= 0.005297 u
∴ अभिक्रिया का Q - मान = ∆m (u) x 931.5 Mev
= 0.005297 x 931.5 MeV
= 4.9342 MeV
मूल नाभिक का परमाणु द्रव्यमान A = 226 
विघटन के बाद बने Rn परमाणु का द्रव्यमान = A - 4
α - कण का परमाणु का द्रव्यमान = 4
यदि विघटन के बाद बने Rn परमाणु का संवेग p_R व α - कण का संवेग से व्यक्त करें तो संवेग संरक्षण के सिद्धान्त से
p_R + P_α = 0 क्योंकि मूल परमाणु का संवेग = 0(शून्य)
p_R = -p_α ...................(1)
उत्पन्न कणों की गतिज ऊर्जा

(b) ₈₆Rn²²⁰ के α - क्षय को निम्न समीकरण से व्यक्त करेंगे-
₈₆Rn²²⁰ → ₈₄Po²¹⁶ + ₂He⁴ + Q
भाग (a) की भाँति गणना करने पर
द्रव्यमान क्षति ∆m = (बायें पक्ष का द्रव्यमान - दायें पक्ष का द्रव्यमान)
= [220.01137 - (216.00189 + 4.002603)]u
= 0.006877 u
∴ Q का मान = ∆m (u) x 931.5 MeV 
= 0.006877 x 931.5
= 6.41 Mev
∴ α - कण की गतिज ऊर्जा

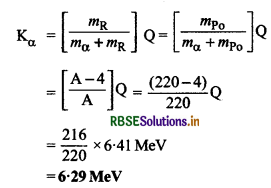
प्रश्न 13. 
रेडियो न्यूक्लाइड ₆C¹¹ का क्षय निम्न - लिखित समीकरण के अनुसार होता है-
₆C¹¹ → ₅B¹¹ + +₁e⁰ +v 
अर्द्ध - आयु T= 20.3 मिनट।
उत्सर्जित पॉजिट्रॉन की अधिकतम ऊर्जा 0.960 MeV है। द्रव्यमानों के निम्नलिखित मान दिये गये हैं-
m(₆C¹¹) = 11.011434 u तथा m(₅B¹¹) = 11.009305 u
Q - मान की गणना कीजिए एवं उत्सर्जित पॉजिट्रॉन की अधिकतम गतिज ऊर्जा के मान से इसकी तुलना कीजिए। 
हल: 
दिया है,

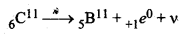
द्रव्यमान क्षति ∆m = [बायें पक्ष का द्रव्यमान - दायें पश्च का द्रव्यमान]
या ∆m = [{m(₆C¹¹) - 6m_e} - {m(₅B¹¹) - 5m_e + m_e}]
= m(₆C¹¹) - m(₅B¹¹) - 2m_e
= 11.011434 - 11.009395 - 2 x 0.000548 
या ∆m = 0.001033 u
∴ Q = ∆m(u) x 931 = 0.001033 x 931
= 0.961 MeV
उत्सर्जित पॉजिट्रॉन की महत्तम गतिज ऊर्जा 0.960 Mev है जो कि Q - मान के तुल्य है।
∵ उत्पाद नाभिक पॉजिट्रॉन की तुलना में अत्यधिक भारी है, अत: इसकी गतिज ऊर्जा नगण्य होगी। चूँकि पॉजिट्रॉन की अधिकतम गतिज ऊर्जा Q - मान के तुल्य है, अत: न्यूट्रिनों भी लगभग शून्य ऊर्जा के साथ उत्सर्जित होगा।

प्रश्न 14. 
₁₀Ne²³ का नाभिक, उत्सर्जन के साथ क्षयित होता है। इस ß- - क्षय के लिए समीकरण लिखिए और उत्सर्जित इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा ज्ञात कीजिए। m(₁₀Ne²³) = 22.994466 u, m(₁₁Na²³) = 22.089770 u
हल: 
₁₀Ne²³ नाभिक के ß - क्षय का समीकरण निम्नलिखित है

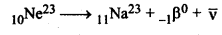
द्रव्यमान क्षति 
∆m = {m(₁₀Ne²³) - 10 m_e} - {m(₁₁Na²³) - 11m_e} - m_e
= m(₁₀Ne²³) - m(₁₁Na²³)
= 22.994466 - 22.989770
∆m = 0.004696 u
∴ Q - मान = 0.004696 x 931 MeV
= 4.37 MeV
∵ ₁₁Na²³ नाभिक ß - कण की तुलना में अत्यधिक भारी है, अतः इसकी गतिज ऊर्जा नगण्य होगी। ß - कण की ऊर्जा अधिकतम होगी यदि एण्टीन्यूट्रिनों शून्य ऊर्जा के साथ उत्सर्जित हो। इस दशा में ß - कण की ऊर्जा अधिकतम ऊर्जा Q - मान के बराबर अर्थात् 4.37 MeV होगी।

प्रश्न 15.
किसी नाभिकीय अभिक्रिया A + b = c + d का Q - मान निम्नलिखित समीकरण द्वारा परिभाषित होता है-
Q = [m_A+m_b - m_c - m_d]c²
यहाँ पर प्रदर्शित सभी द्रव्यमान विराम द्रव्यमान (rest mass) हैं। दिवे गये आंकड़ों के आधार पर बताइये कि निम्नलिखित अभिक्रियाएँ ऊष्माक्षेपी हैं या ऊष्माशोषी (exothermic or endothermic)?

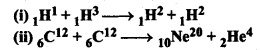
दिये गये परमाणु दव्यमान निम्नलिखित हैं-
m(₁H²) = 2.014102 u, m(₁H³) = 3.016049u, m(₆C¹²) = 12.00000 u, m(₁₀Ne²⁰) = 19.992439 u 
उत्तर:
दी गई अभिक्रिया
₁H¹ + ₁H³ → ₁H² + ₁H²
इस अभिक्रिया के लिए 
Q = [m (₁H²) + m(₁H³) - {m(₁H²) + m(₁H²)}]c²
= (4.023874 - 4.028204) x 931.5 MeV
= -0.0043 x 931.5 MeV
= -4.033 MeV
Q का ऋणात्मक मान यह दर्शाता है कि अभिक्रिया ऊष्माशोषी है। 

(ii)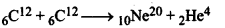
Q = [2m(₆C¹¹²) - {m(₁₀Ne²⁰) + m(₂He⁴)}]c²
= [2 x 12.000000 - (19.992439 + 4.002603)] x 931.5 MeV
= (24 - 23.99504) x 931.5 MeV
= 4.618 MeV
Q का धनात्मक मान यह दर्शाता है कि अभिक्रिया ऊष्माउन्मोची है।

प्रश्न 16. 
माना कि हम ₂₆Fe⁵⁶ नाभिक के दो समान अवयवों ₁₃Al²⁸ में विखण्डन पर विचार करें। क्या ऊर्जा की दृष्टि से यह विखण्डन सम्भव है? इस प्रक्रम का मान ज्ञात करके अपना तर्क प्रस्तुत करें। दिया है: m(₂₆Fe⁵⁶) = 55.93494 u; m(₁₃Al²⁸) = 27.98191 u
उत्तर: 
सम्भावित अभिक्रिया निम्न प्रकार होगी-

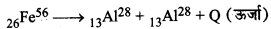
इस अभिक्रिया में द्रव्यमान क्षति
∆ m = m(₂₆Fe⁵⁶) - 2m(₁₃Al²⁸)
= (55.93494 - 2 x 27.98191) u
= -0.2888 u
∴ Q = -0.2888 x 931.5 MeV
या Q = -26.90 MeV
बँकि अभिक्रिया का Q - मान ऋणात्मक है अतः क्रिया सम्भव नहीं है।

प्रश्न 17.
₉₄Pu²³⁹ के विखण्डन गुण बहुत कुछ ₉₂U²³⁵ से मिलते - जुलते हैं। प्रति विखण्डन विमुक्त औसत ऊर्जा 180 MeV है। यदि 1kg शुद्ध ₉₄Pu²³⁹ के सभी परमाणु विखण्डित हों तो कितनी MeV ऊर्जा विमुक्त होगी?
हल: 
यहाँ ₉₄Pu²³⁹ के एक विखण्डन में मुक्त ऊर्जा = 180 Mev 
₉₄Pu²³⁹ का ग्राम परमाणु द्रव्यमान = 239g 
239g प्लूटोनियम में परमाणुओं की संख्या
= N_A = 6.02 x 10²³
∴ 1kg अर्थात् 1000g  प्लूटोनियम में परमाणुओं की संख्या
N = \(\frac{\mathrm{N}_{\mathrm{A}} \times 1000}{239}=\frac{602 \times 10^{23} \times 1000}{239}\)
= 2.52 x 10²⁴
∵ 1 परमाणु के विखण्डन में मुक्त कर्जा = 180 MeV
∴ N अर्थात् 2.52 x 10²⁴ परमाणुओं के विखण्डन से
मुक्त कुल ऊर्जा =N x 180 MeV
= 22.52 x 10²⁴ x 180 MeV
= 4.536 x 10²⁶ MeV

प्रश्न 18.
किसी 1000 MW विखण्डन रिएक्टर के आधे ईधन का 5.0 वर्ष में व्यय (consumes) हो जाता है। प्रारम्भ में इसमें कितना ₉₂U²³⁵ था? मान लीजिए कि रिएक्टर 80% समय कार्यरत रहता है, इसकी सम्पूर्ण ऊर्जा ₉₂U²³⁵ के विखण्डन से ही उत्पन्न हुई है, तथा ₉₂U²³⁵ न्यूक्लाइड केवल विखण्डन प्रक्रिया में ही व्यय होता है। 
उत्तर:
रिएक्टर की शक्ति = 1000 MW
= 1000 x 10⁶ W = 10⁹ W या 10⁹ Js^-1 
समय t = 5.0 वर्ष = 5 x 365 x 24 x 3600 s
= 1.577 x 10⁸
∴ रिएक्टर 80% समय तक कार्यरत रहता है।
∴ 5 वर्ष में रियेक्टर में उत्पन्न ऊर्जा
E = \(\frac{80}{100}\) x P x t
E = \(\frac{80}{100}\) x 10⁹ x 1.577 x 10⁸
E = 1.2616 x 10¹⁷ J
∵ यूरेनियम के एक विखण्डन में मुक्त ऊर्जा = 200 MeV
अर्थात् 200 MeV या 200 x 1.6 x 10^-13 J ऊर्जा उत्पन्न होती है = 1 
परमाणु से
∴ 1 J ऊर्जा उत्पन्न होगी
= \(\frac{1}{200 \times 16 \times 10^{-13}}\) परमाणुओं से
∴ 1.2616 x 10¹⁷ ऊर्जा उत्पन होगी = \(\frac{1.2616 \times 10^{17}}{200 \times 16 \times 10^{-13}}\)
परमाणुओं से = 3.94 x 10²⁷ परमाणुओं से 
∴ 5 वर्ष में विखण्डित नाभिकों की संख्या
n = 3.94 x 10²⁷ परमाणु 
∵ 6.02 x 10²³ परमाणुओं का द्रव्यमान = 235 g
∴ 3.94 x 10²⁷  परमाणुओं का द्रव्यमान
\(=\frac{235 \times 3.94 \times 10^{27}}{6.02 \times 10^{23}}\)
= 1.544 x 10⁶ g
= 1.544 x 10³ kg
= 1544 kg
∵ 5.0 वर्ष में आधी मात्रा विघटित हो जाती है।
∴ रियेक्टर में यूरेनियम - 235 की प्रारम्भिक मात्रा 
= 2 x 1544
= 3088 kg

प्रश्न 19.
2.0 kg इयूटीरियम के संलयन से एक 100 W का विद्युत लैम्प कितनी देर प्रकाशित (glowing) रखा जा सकता है? संलयन अभिक्रिया निम्न प्रकार ली जा सकती है
₁H² + ₁H² → ₂He³ + ₀n¹ + 3.27 MeV
हल: 
लैम्प की शक्ति P= 100W, ड्यूटीरियम का द्रव्यमान = 2 kg 
दिया गया समी.
₁H² + ₁H² → ₂He³ + ₀n¹ + 3.27 MeV
स्पष्ट है कि ड्यूटीरियम (₁H²) के दो नाभिकों के संलयन से 3.27 MeV ऊर्जा उत्पन्न होती है।
∵ ड्यूटीरियम का परमाणु द्रव्यमान = 2 g
अत: 2 g ड्यूटीरियम में उपस्थित नाभिकों की संख्या
= N_A = 6.02 x 10²³
∴ 2 kg अर्थात् 2000 g यूटीरियम में नाभिकों की संख्या-
n = \(\frac{602 \times 10^{23} \times 2000}{2}\)
= 6.02 x 10²⁶
∴ होने वाले कुल संलयनों की संख्या
n' = \(\frac{n}{2}=\frac{6.02 \times 10^{26}}{2}\)
∵ एक संलयन से प्राप्त ऊर्जा = 3.27 MeV
= 3.27 x 1.6 x 10^-13 J
अत: 2 kg ड्यूटीरियम के संलयन से प्राप्त कुल ऊर्जा
E = n' x 3.27 x 1.6 x 10^-13 J
= \(\frac{6.02 \times 10^{26}}{2}\) x 3.27 x 1.6 x 10-13 J
= 15.748 x 10¹³ J
∵ 100 W के बल्ब द्वारा 1 sec  में व्यय ऊर्जा = 100 J 
∴ वह समय जब तक बल्ब प्रकाशित रह सकता है
t = \(\frac{\mathrm{E}}{100} \mathrm{~s}=\frac{15.748 \times 10^{13}}{100} \mathrm{~s}\)
= 15.748 x 10¹¹ s
= \(\frac{15.748 \times 10^{11}}{365 \times 24 \times 3600}\) वर्ष
=0.0000499 x 10⁹
= 4.99 x 10⁴ वर्ष 

प्रश्न 20. 
दो युट्रॉनों के आमने - सामने की टक्कर (head - on collision) के लिए कूलॉम अवरोध (coulomb barrier) की ऊँचाई ज्ञात कीजिए। (संकेत - कूलॉम अवरोध वह न्यूनतम गतिज ऊर्जा है जिसके द्वारा उन्हें एक - दूसरे की ओर भेजे जाने पर वे कूलॉमीय बल के विरुद्ध परस्पर संलयित हो सकें। यह मान सकते हैं कि इखूट्रॉन 2.0 फर्मी प्रभावी त्रिज्या वाले दृढ़ गोले हैं)।
हल: 
आमने - सामने टक्कर में दोनों ड्यूट्रॉनों के केन्द्रों के मध्य दूरी = 2 x त्रिज्या = 2 x 2 फर्मी = 4 फर्मी
= 4 x 10^-15 m 
प्रत्येक ड्यूट्रॉन पर आवेश = e = 1.6 x 10^-19 C
∴ टक्कर के समय ड्यूट्रॉनों की वैद्युत स्थितिज ऊर्जा

या K = 180 keV
∴ कूलॉम अवरोध की ऊँचाई अर्थात् प्राचीर = 180 keV

प्रश्न 21. 
समीकरण R = R₀(A)^1/3 के आधार पर दर्शाइये कि नाभिकीय द्रव्य का घनत्व लगभग अचर है (अर्थात् A पर निर्भर नहीं करता है)। यहाँ R₀ एक नियतांक है एवं A नाभिक की द्रव्यमान संख्या
उत्तर:
नाभिक के दव्य का घनत्व 

या ρ = \(\frac{m \mathrm{~A}}{4 \pi \mathrm{R}^3}\) जहाँ m = एक न्यूक्लिऑन का औसत द्रव्यमान 
नाभिक त्रिज्या R = R₀(A)^1/3 का प्रयोग करने पर
\(\rho=\frac{m \mathrm{~A}}{\frac{4}{3} \pi\left[R_0(\mathrm{~A})^{1 / 3}\right]^3}=\frac{3 m \mathrm{~A}}{4 \pi \mathrm{R}_0^3 \mathrm{~A}}\)
या \(\rho=\frac{3 m}{4 \pi \mathrm{R}_0{ }^3}\)
∵ R₀ नियतांक है और इस सूत्र में A नहीं है। अत: नाभिक का घनत्व नियतांक है और A पर निर्भर नहीं करता है।

प्रश्न 22. 
किसी नाभिक ß⁺ (पॉजिट्रॉन) उत्सर्जन की एक अन्य प्रतियोगी प्रक्रिया है जिसे इलेक्ट्रॉन परिग्रहण (capture) कहते हैं (इसमें परमाणुकी आन्तरिक कक्षा, जैसे किर - कक्षा, से नाभिक एक इलेक्ट्रॉन परिग्रहीत (captured) कर लेता है और एक न्यूट्रिनों (v) उत्सर्जित करता है।

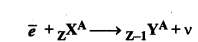
दर्शाइये यदि ß⁺ उत्सर्जन ऊर्जा विचार से अनुमत है तो इलेक्ट्रॉन परिग्रहण भी आवश्यक रूप से अनुमत (allowed) है, परन्तु इसका विलोम अनुमत नहीं है।
उत्तर:
किसी नाभिक से ß⁺ का उत्सर्जन निम्न प्रकार प्रदर्शित कर सकते है-
_ZX^A = _Z-1Y^A + ₊₁E⁰ + v + Q₁ ............(1) 
दूसरी इलेक्ट्रॉन परिग्रहण की प्रक्रिया निम्न प्रकार दिखा सकते हैं-
_ZX^A + ₁e⁰ = _Z-1Y^A + v + Q₂ ............(2)
समी. (1) में मुक्त ऊर्जा Q₁ निम्न सूत्र से मिलेगी-

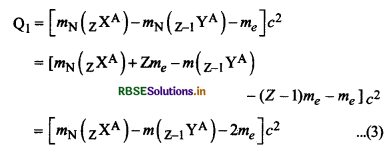
यहाँ m_N नाभिक के द्रव्यमान के लिए प्रयोग किया गया है। इसी प्रकार समी. (2) से मुक्त ऊर्जा

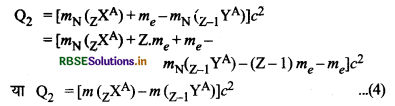
समी. (3) व (4) से स्पष्ट है कि
Q₁ < Q₂
यदि पॉजिट्रॉन उत्सर्जन (अभिक्रिया - 1) ऊर्जा दृष्टि से अनुमत है तो इस क्रिया का मान धनात्मक होगा अर्थात्
Q₁ > 0 
∵ Q₂ > Q₁ ∴ Q₂ > 0 क्योंकि Q₁ > 0
अर्थात् तब अभिक्रिया (2) का Q मान भी धनात्मक होगा अर्थात ऊर्जा दृष्टि से इलेक्ट्रॉन परिग्रहण भी अनुमत है।
अब इस क्रिया के विलोम पर विचार करते हैं।
Q₂ > 0 का अर्थ आवश्यक रूप से यह नहीं है कि Q₁ > 0 हो क्योंकि Q₂ > Q₁ अत: अभिक्रिया का विलोम सत्य नहीं है।

प्रश्न 23.
आवर्त सारणी (periodic table) में मैग्नीशियम का औसत परमाणु द्रव्यमान 24.312 u दिया गया है। यह औसत मान, पृथ्वी पर इसके समस्थानिकों की सापेक्ष बहुलता (abundance) के आधार पर दिया गया है। मैग्नीशियम के तीनों समस्थानिक तथा उनके द्रव्यमान इस प्रकार हैं- ₁₂Mg²⁴ (23.985044 u), ₁₂Mg²⁵ (24.98584 u), ₁₂M²⁶ (25.98259 u)। प्रकृति में प्राप्त मैग्नीशियम में ₁₂Mg²⁴ की (द्रव्यमान के अनुसार) बहुलता 78.99% है। अन्य दोनों समस्थानिकों की बहुलता का परिकलन (ealculate) कीजिए। 
हल:
दिया है: 
मैग्नीशियम का औसत परमाणु द्रव्यमान =24.312 u
₁₂Mg²⁴ समस्थानिक की बहुलता= 78.99% 
माना ₁₂Mg²⁵ की बहुलता = α % 
तो ₁₂Mg²⁶ की बहुलता = (100 - 78.99) - α
= (21.01 - α)% 
अतः तीनों समस्थानिकों को निम्न तालिका के अनुसार दिखा सकते

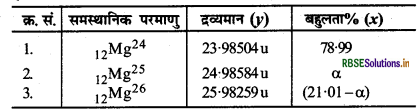
∴ औसत परमाणु - द्रव्यमान = \(\frac{\Sigma x y}{\Sigma x}\)
या 24.312 u
\(\begin{aligned} &(23.9854 \times 78-99)+(24.98584 \times \alpha)+\\ &=\frac{\{2598259 \times(2101-\alpha)\}}{7899+\alpha+(2101-\alpha)} \mathrm{u} \end{aligned}\)
\(=\frac{189458+24.98584 \dot{\alpha}+545894-25982596 \alpha}{100} \mathrm{u}\)
या 2431.2 = 2440.474 - 0.99675 α
या 0.99675 α = 2440.474 - 2431.2 = 9.274
∴\( \alpha=\frac{9 \cdot 274}{0.99675}=9 \cdot 30\)
तथा 21.01 - α = 21.01 - 9.30 = 11.70
इसी प्रकार ₁₂Mg²⁵ की बहुलता = 9.30%
और ₁₂Mg²⁶ की बहुलता = 11.70%

प्रश्न 24. 
न्यूट्रॉन पृथक्करण ऊर्जा (separation energy), परिभाषा के अनुसार वह ऊर्जा है जो किसी नाभिक से एक न्यूट्रॉन को निकालने के लिए आवश्यक होती है। नीचे दिये गये आँकड़ों का इस्तेमाल करके ₂₀Ca⁴¹ एवं ₁₃Al²⁷ नाभिकों की न्यूट्रॉन पृथक्करण ऊर्जा ज्ञात कीजिए।
m(₂₀Ca⁴⁰) = 39.962591 u
m(₂₀Ca⁴¹) = 40.962278 u
m(₁₃Al²⁶) = 25.986895 u
m(₁₃Al²⁷) = 26.981541 u
हल:
₁₀Ca⁴¹ की न्यूट्रॉन पृथक्करण ऊर्जा-
₂₀Ca⁴¹ से न्यूट्रॉन पृथक्करण अभिक्रिया का समीकरण-

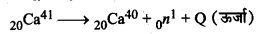
∴ Q = [m(₂₀Ca⁴¹) - m(₂₀Ca⁴⁰) - m_n] x 931.5 MeV
= [40.962278 - 39.962591 - 1.008665] x 931.5 MeV
= -0.008978 x 931.5 MeV
या Q = -8.36 MeV
Q का मान ऋणात्मक है अतः अभिक्रिया ऊष्माशोषी (endothermic) है।
∴ न्यूट्रॉन पृथक्करण ऊर्जा = 8.36 MeV
₁₃Al²⁷ की न्यूट्रॉन पृथक्करण ऊर्जा (neutron separation energy)
₁₃Al²⁷ से न्यूट्रॉन पृथक्करण अभिक्रिया का समीकरण 

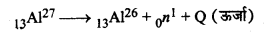
∴ Q = [m(₁₃Al²⁷) - m(₁₃Al²⁶) - m_n]  x 931.5 MeV
=[26.98141 - 25.986895 - 1.008665] x 931.5 MeV
= -0.014019 x 931.5 MeV
= -13.06 MeV
इस अभिक्रिया में भी Q का मान ऋणात्मक है अत: यह अभिक्रिया भी ऊष्माशोषी है।
∴ न्यूट्रॉन पृथक्करण ऊर्जा = 13.06 MeV

प्रश्न 25.
किसी स्त्रोत में फॉस्फोरस के दो रेडियो न्यूक्लाइड निहित हैं ₁₅P³² (अर्द्ध - आयु T = 14.3 दिन) एवं ₁₅P³³ (T = 25.3 दिन)। प्रारम्भ में ₁₅P³³ से 10% क्षय प्राप्त होता है। इससे 90% क्षय प्राप्त करने के लिए कितने समय प्रतीक्षा (how long one must wait) करनी होगी?
हल:
माना प्रारम्भ में ₁₅P³³ तथा ₁₅P³² को रेडियोएक्टिव सक्रियताएँ R_o1 व R_o2 हैं तथा t समय बाद क्रमश: R₁ व R₂ हैं।
∴ प्रारम्भ में कुल सक्रियता = R₀₁ +R_o2
∵ R₀₁ = प्रारम्भिक सक्रियता का 10%
∴ R₀₁ = \(\frac{10}{100}\) (R₀₁ + R₀₂)
या 10 R₀₁ = R₀₁ + R₀₂
या 9 R₀₁ = R₀₂ ..............(1)
समय t के बाद कुल सक्रियता = (R₁ + R₂)
और R₁ = कुल सक्रियता का 90%
∴ R₁ = \(\frac{90}{100}\) (R₁ + R₂)
या 10R₁ = 9R₁ + 9R₂
या R₁ = 9R₂ ............(2)
समी. (2) को (1) से भाग देने पर

या \(\left(\frac{25 \cdot 3-14 \cdot 3}{14 \cdot 3 \times 25 \cdot 3}\right) t=\frac{4 \cdot 3953}{0.6931}\)
या t = \(\frac{4.3953 \times 14.3 \times 25.3}{0.6931 \times 11}\)
या t = 209 दिन
वैकल्पिक विधि-
माना प्रारम्भ में स्रोत में 90% ₁₅P₁³² व 10% ₁₅P₂³³ हैं। माना n दिनों के पश्चात् स्रोत में 90% ₁₅P₂³³ और 10% ₁₅P₁³²
माना प्रारम्भ में स्रोत में 9x ग्राम P₁ और x ग्राम P₂ है। x दिनों के पश्चात् P₁ की मात्रा y ग्राम और P₂ की मात्रा 9y ग्राम है।
M = M₀.2^-t/T1/2 से,
y = 9x.2^-t/14.3 ...........(1)
9y = x.2^-t/25.3 ..........(2)
अत: (1) व (2) से,

= 208:51 ≈ 209 दिन 

प्रश्न 26.
कुछ विशिष्ट परिस्थितियों (certain circumstances) में एक नाभिक, α - कण से अधिक द्रव्यमान वाला एक कण उत्सजित करके क्षयित होता है। निम्नलिखित क्षय प्रक्रियाओं पर विचार कीजिए
₈₈Ra²²³ → ₈₂Pb²⁰⁹ + ₆Cl¹⁴
₈₈Ra²²³ → ₈₆Rn²¹⁹ + ₂He⁴
इन दोनों क्षय प्रक्रियाओं के लिए Q मान की गणना कीजिए और दर्शाइये कि दोनों प्रक्रियाएँ ऊर्जा की दृष्टि से सम्भव हैं।
हल:
(a) क्षय की प्रथम अभिक्रिया-
₈₈Ra²²³ → ₈₂Pb²⁰⁹ + ₆Cl¹⁴ + Q
∴ द्रव्यमान क्षति
∆m = [m(₈₈Ra²²³) - {m(₈₂Pb²⁰⁹) +m(₆Cl¹⁴)}] u
= [223.01850 - (208.98107 + 14.00324)] u
= 0.03419 u
∴ Q = ∆m (u) x 931 MeV = 0.03419 x 931
= 31.83 MeV

(b) क्षय की दूसरी अभिक्रिया-
₈₈Ra²³³ → ₈₆Rn²¹⁹ + ₂He⁴ + Q
∴ द्रव्यमान क्षति-
∆m = [m(₈₈Ra²²³) - {m(₈₆Rn²¹⁹) +m(₂He⁴)}]
= [223.01850 - (219.00948 + 4.00260)] u
= 0.00642 u
∴ Q = 0.00642 x 931 = 5.98 MeV
चूँकि दोनों अभिक्रियाओं के लिए Q के मान धनात्मक है अत: दोनों अभिक्रियाएँ ऊर्जा की दृष्टि से सम्भव हैं।

प्रश्न 27. 
तीव्र न्यूट्रॉनों द्वारा ₉₂U²³⁸ के विखण्डन पर विचार कीजिए। किसी विखण्डन प्रक्रिया में प्राथमिक अंशों (Primary fragments) के ß - क्षय के पश्चात् कोई न्यूट्रॉन उत्सर्जित नहीं होता तथा ₅₈Ce¹⁴⁰ तथा ₃₄Ru⁹⁹ अन्तिम उत्पाद होते हैं। विखण्डन प्रक्रिया के लिए Q - मान का परिकलन कीजिए। आवश्यक आँकड़े इस प्रकार हैं
m(₉₂U²³⁸) = 238.05079 u, m(₅₈Ce¹⁴⁰) = 139.90543 u, m(₃₄Ru⁹⁹) = 98.90594 u
हल: 
विखण्डन अभिक्रिया का समीकरण-
₉₂U²³⁸ +₀n¹ → ₅₈Ce¹⁴⁰ + ₃₄Ru⁹⁹ + Q
∴ द्रव्यमान क्षति-
∆m = [m(₉₂U²³⁸) +m_n - {(₅₈Ce¹⁴⁰) +m(₃₄Ru⁹⁹)}]
= [238.05079 + 1.00867 - (139.90543 + 98.90594)]u
= 0.24809 u
Q = ∆m (u) x 931.5 MeV
= 0.24809 x 931.5 MeV
= 231.1 MeV

प्रश्न 28. 
D - T अभिक्रिया (ड्यूटीरियम - ट्राइटियम संलयन),
₁H² + ₁H³ → ₂He⁴ + n 
पर विचार कीजिए।
(a) नीचे दिये गये आंकड़ों के आधार पर अभिक्रिया में विमुक्त ऊर्जा का मान Mev में ज्ञात कीजिए।
m(₁H²) = 2.014102 u,
m(₁H³) = 3.016049 u
(b) ड्यूटीरियम एवं दाइटियम दोनों की त्रिज्या लगभग 1.5 fm मान लीजिए। इस अभिक्रिया में, दोनों (to overcome the coulomb repulsion) नाभिकों के मध्य कूलोम प्रतिकर्षण से पार पाने के लिए कितनी गतिज ऊर्जा की आवश्यकता है? अभिक्रिया प्रारम्भ करने के लिए गैसों (D तथा T) को किस ताप तक ऊष्मित किया जाना चाहिए?
(संकेत: किसी संलयन प्रक्रिया के लिए आवश्यक गतिज ऊर्जा = संलयन क्रिया में संलग्न कणों की औसत तापीय गतिज ऊर्जा = \(2\left(\frac{3 k \mathrm{~T}}{2}\right))\), जहाँ K वोल्ट्जमैन नियतांक और T परमताप है।)
उत्तर:
(a) दी गई अभिक्रिया-
₁H² + ₁H³ → ₂He⁴ + ₀n¹ + Q
Q = [m(₁H²) + m(₁H³) - m(₂He⁴) - m_n] x 931 Mev 
= [2.014102 + 3.016049 - 4.002603 - 1.00867] x 931 Mev 
= 30.018878 x 931 MeV
= 17.58 MeV 

(b) दोनों नाभिकों को वैद्युत स्थितिज कर्जा जब वे एक - दूसरे को स्पर्श कर रहे होते हैं-

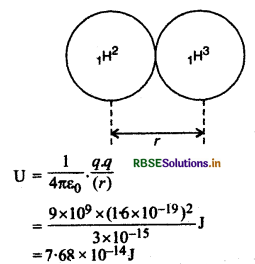
चूंकि दोनों नाभिकों के वैद्युत प्रतिकर्षण के विरुद्ध गतिज ऊर्जा के कारण ही नाभिक संलयन कर पाते हैं अतः कुल गतिज ऊर्जा
K = 2 x \(\frac{3}{2} k \mathrm{~T}\) = 3kT 
या T = \(\frac{\mathrm{K}}{3 k}=\frac{\mathrm{U}}{3 k}=\frac{7.68 \times 10^{-14}}{3 \times 1.38 \times 10^{-23}}\)
= 1.85 x 10⁹ K
वास्तव में अभिक्रिया को प्रारम्भ करने के लिए कुछ कम ताप की आवश्यकता होती है।

प्रश्न 29. 
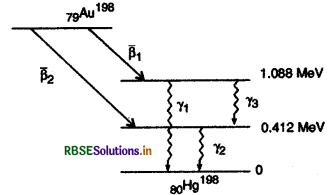
नीचे दी गई भय योजना में, γ - क्षयों की विकिरण आवृत्तियाँ एवं ß - कणों की अधिकतम गतिज ऊर्जाएँ ज्ञात कीजिए। दिया है-
m(₇₉Au¹⁹⁸) = 197.968233 u
m(₈₀Hg¹⁹⁸) = 197.966760 u

उत्तर:
γ - कोटॉन की ऊर्जा
E₁ = 1.088 - 0 = 1.088 MeV
= 1.088 x 1.6 x 10^-15 J
∴ γ₁ फोटॉन की आवृत्ति
v₁ = \(\frac{E_1}{h} = \frac{1088 \times 16 \times 10^{-13}}{66 \times 10^{-34}}\)
= 2.63 x 10²⁰ Hz
γ₂ - फोटॉन की ऊर्जा, E₂ = 0.412 - 0 = 0.412 MeV
या E₂ = 0.412 x 1.6 x 10^-13 J
∴ आवृत्ति v₂ = \(\frac{E_2}{h}=\frac{0.412 \times 16 \times 10^{-13}}{66 \times 10^{-34}}\)
= 9.88 x 10¹⁹ Hz
γ₃ - फोटॉन की ऊर्जा,
E₃ = (1.088 - 0.412) = 0.676 MeV
= 0.676 x 1.6 x 10^-13 J
∴ आवृत्ति v₃ = \(\frac{E_3}{h}=\frac{0 \cdot 676 \times 1 \cdot 6 \times 10^{-13}}{6 \cdot 6 \times 10^{-34}}\)
ß₁ - कण की अधिकतम गतिज ऊर्जा
K_max (ß₁) = [m(₇₉Au¹⁹⁸) - ₈₀Hg¹⁹⁸ का द्वितीय उत्तेजित कक्षा में द्रव्यमान] x 931 MeV
= [m(₇₉Au¹⁹⁸) - m(₈₀Hg¹⁹⁸) - \(\frac{1.088}{931}\)] x 931 MeV
= 931 [197.968233 - 197.966760] - 1.088
= 1.371 - 1.038 = 0.283 MeV
इसी प्रकार हल करके ज्ञात करने पर
Kmax (ß₂) = 0.957 MeV