RBSE Solutions for Class 12 Physics Chapter 13 Nuclei

Rajasthan Board RBSE Solutions for Class 12 Physics Chapter 13 Nuclei Textbook Exercise Questions and Answers.

RBSE Class 12 Physics Solutions Chapter 13 Nuclei

RBSE Class 12 Physics Nuclei Textbook Questions and Answers

Question 13.1.
(a) Two stable isotopes of lithium ⁶₃Li and ⁷₃Li have respective abundances of 7.5% and 92.5%. These isotopes have masses 6.01512 u and 7.01600 u respectively. Find the atomic mass of lithium.
(b) Boron has two stable isotopes ¹⁰₅B and ¹¹₅B. Their respective masses are 10.01294 u and 11.00931 u and the atomic mass of boron is 10.811 u. Find the abundances of ¹⁰₅B and ¹¹₅B.
Answer:
(a) Mass of ⁶₃Li = 6.01512 u
Mass of ⁷₃Li =7.01600 u
Abundance of ⁶₃Li = 7.5%
Abundance of ⁷₃Li = 92.5%
∴ Atomic weight of lithium
= \(\frac{7.5 \times 6.01512+92.5 \times 7.01600}{100}\) u
= \(\frac{45.1134+648.98}{100}\) u
= 6.941 u.

(b) Mass of ¹⁰₅B = 10.01294 u
Mass of ¹¹₅B = 11.00931 u
Atomic weight of boron = 10.811 u
Let abundance of ¹⁰₅B = x %
∴ Abundance of ¹¹₅B = (100 - x)%
Since atomic weight

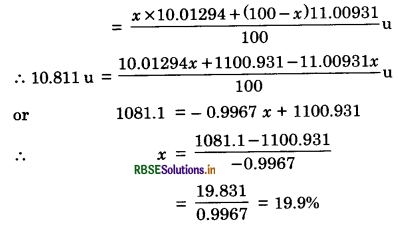
∴ Abundance of ¹⁰₅B = 19.9%.
And abundance of ¹¹₅B = 100 - 19.9 = 80.1%.

Question 13.2.
The three stable isotopes of neon: ²⁰₁₀Ne, ²¹₁₀Ne, ²²₁₀Ne, have respective abundances of 90.51%, 0.27%, 9.22%. The atomic masses of these isotopes are 19.99 u and 21.99 u respectively. Obtain the average atomic mass of neon.
Answer:
The average atomic mass of neon is
m(Ne) = \(\frac{90.51 \times 19.99+0.27 \times 20.99+9.22 \times 21.99}{90.51+0.27+9.22}\)
or m(Ne) = [90.51 x 19.99 + 0.27 x 20.99 + 9.22 x 21.99] x 10^-2
= 20.18 u.

Question 13.3.
Obtain the binding energy of a nitrogen nucleus (¹⁴₇N). Given m ¹⁴₇N = 14.00307 u.
Answer:
Here Z = 7 and A = 14, A - Z = 14 - 7 = 7
∴ Mass defect
∆m = [Zm_H + (A - Z)m_n - m_N]u
= (7 x 1.00783 + 7 x 1.00867 - 14.00307) u
= (7.05481 + 7.06069 - 14.00307) u
= 0.11243 u
Since 1 u = 931.5 MeV
∴ B.E. of ¹⁴₇N = 0.11243 x 931 MeV= 104.7 MeV.

Question 13.4.
Obtain the binding energy of the nuclei ⁵⁶₂₆Fe and ²⁰⁹₈₃Bi in unit of MeV from the following data:
m(⁵⁶₂₆Fe) = 55.934939 u, m(²⁰⁹₈₃Bi) = 208.980388 u
Answer:
B.E. of ⁵⁶₂₆Fe
= [Zm_H+(A - Z)m_N - m(^A_ZX)] 931.5
= [{26 x 1.007825 + (56 - 26) x 1.008665} - 55.934939] 931.5
= [{26.20345 + 30.25995} - 55.934939] 931.5
= 492.26 MeV

B.E. of ²⁰⁹₈₃Bi
= [{83 x 1.007825 + (209 - 83) x 1.008665} - 208.980388] 931.5
= [{83.64975 + 127.09179 - 208.980388] 931.5
= 1640.1 MeV.
B.E. per nucleon = \(\frac{1640.1}{209}\) = 7.84 MeV
Fe56 has greater binding energy per nucleon.

Question 13.5.
A given coin has a mass of 3.0 g. Calculate the nuclear energy that would be required to separate all the neutrons and protons from each other. For simplicity assume that the coin is entirely made of ⁶³₂₉Cu atoms (of mass 62.92960 u).
Answer:
Here Z = 29, A - 63, so A - Z = 34
Mass defect
∆m - (Zm_H + (A - Z)m_n - m_N) u
= [29 x 1.00783 + 34 x 1.00867 - 62.92960] u
= 0.592254 u
Since 1 u = 931.5 MeV
∴ B.E. of ⁶³₂₉Cu
= 0.592254 x 931.5
= 551.68 MeV
Since 63 g of ⁶³₂₉Cu contains 6 x 10²³ atom so 3 g of ⁶³₂₉Cu contains \(\frac{3 \times 6 \times 10^{23}}{63}=\frac{2}{7}\) x 10²³
∴ Total energy required to separate neutrons and protons from each other of 3.0 g Cu.
or E = \(\frac{2}{7}\) x 10²³ x 551.67
= 157.6 x 10²³
= 1.584 x 10²⁵ MeV.

Question 13.6.
Write nuclear reaction equations for
(i) α-decay of ²²⁶₈₈Ra
(ii) α-deacy of ²⁴²₉₄Pu
(iii) ß- -decay pf ³²₁₅P
(iv) ß- -decay of ²¹⁰₈₃Bi
(v) ß+-decay of ¹¹₆C
(vi) ß+-decay of ⁹⁷₄₃Tc
(vii) Electron capture of ¹²⁰₅₄Xe
Answer:

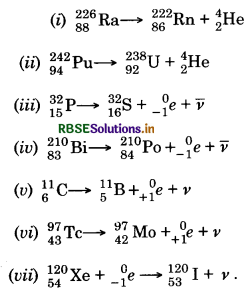
Question 13.7.
A radioactive isotope has a half-life of T years. After how much time is its activity reduced to (a) 3.125% (b) 1% of its original value?
Answer:
(a) Half-life = T years,

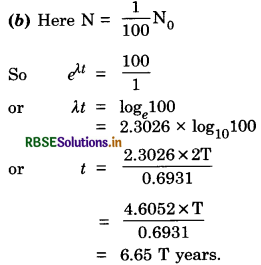
Question 13.8.
The normal activity of living carbon containing matter is found to be about 15 decays per minute for every gram of carbon. This activity arises from the small proportion of radioactive ¹⁴₆C present with the ordinary carbon isotope ¹²₆C. When the organism is dead, its interaction with atmosphere (which maintains the above equilibrium activity) ceases and its activity begins to drop. From the known half-life (= 5730 years) of ¹⁴₆C, and the measured activity, the age of the specimen can approximately be estimated. This is the principle of ¹⁴₆C dating used in archaeology. Suppose a specimen from Mohen-jo-daro gives an activity of 9 decays per minute per gram of carbon. Estimate the approximate age of Indus-Valley civilization.
Answer:
We know that N = N₀e^-λt
Now, activity is proportional to the number of radioactive atoms. So
e^-λt = \(\frac{9}{15}\)
i.e. t = \(\frac{1}{\lambda} \log _e\left(\frac{5}{3}\right)\)
λ is related to half-life T by the relation log 

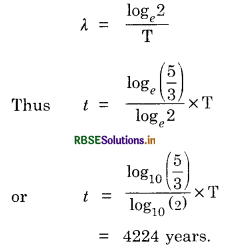
Question 13.9.
Obtain the amount of ⁶⁰₂₇Co necessary to provide a radioactive source of 8.0 m ci strength. The half-life of  ⁶⁰₂₇Co is 5.3 years.
Answer:
The rate of decay of radioactive material is given by

= 7.133 x 10¹⁶ atoms.
Since 60 g of Co contains 6.03 x 10²³ atoms.
∴ Amount necessary to obtain a source of required strength is
= \(\frac{60 \times 7.133 \times 10^{16}}{6.03 \times 10^{23}}\) g
= 7.11 x 10^-6 g.

Question 13.10.
The half life of ⁹⁰₃₈Sr is 28 years.What is the disintegration rate of 15 mg of this isotope?
Answer:
λ = \(\frac{0.693}{\mathrm{~T}}\)
Since 90 g of Sr contains 6.023 x 10²³ atoms
∴ 15 x 10^-3 g of Sr contains \(\frac{6.023 \times 10^{23}}{90}\) x 15 x 10^-3

Question 13.11.
Obtain approximately the ratio of the nuclear radii of the gold isotope ¹⁹⁷₇₉Au and the silver isotope ¹⁰⁷₄₇Ag.
Answer:
Here A₁ = 197 and A₂ = 107
∴ \(\frac{\mathrm{R}_1}{\mathrm{R}_2}=\left(\frac{19.7}{107}\right)^{\frac{1}{3}}\) = 1.23.

Question 13.12.
Find the Q-value and kinetic energy of the emitted α-particle in the α-decay of (a) ²²⁶₈₈Ra (b) ²²⁰₈₆Rn. Given m(²²⁶₈₈Ra) = 226.02540 u m = 222.01750 u, m(²²⁰₈₆Rn) = 220.01137 u, m(²¹⁶₈₄Po) = 216.00189 u. ⁴₂He = 4.002603 amu.
Answer:
(a) The decay takes place according to the equation
²²⁶₈₈Ra → ⁴₂He + ²²²₈₆Rn + Q
Q-value of this reaction
= m(²²⁶₈₈Ra) - [m(⁴₂He) + m(²²²₈₆Rn)]
= [226.02540 - (4.002603 + 222.01750)] u
= [226.02540 - 226.0201] u
= 0.005297 u
= 0.005297 x 931.5 MeV
= 4.9342 MeV.
K.E. of emitted α-particle
= \(\frac{\mathrm{A}-4}{\mathrm{~A}} Q = \frac{226-4}{226}\) x 4.934
= 4.85 MeV

(b) The decay takes place according to the equation
²²⁰₈₆Rn → ⁴₂He + ²¹⁶₈₄Po + Q
Q-value of this reaction
m(²²⁰₈₆Rn) - [m(⁴₂He) + m(²¹⁶₈₄Po)]
= [220.01137 - (4.002603 + 216.00189)] u
= [220.01137 - 220.00449] u
= 0.006877 u
= 0.006877 x 931.5
= 6.41 MeV.

K.E. of emitted α-particle
= \(\frac{\mathrm{A}-4}{\mathrm{~A}}\) Q = \(\frac{220-4}{220}\) x 6.41
= 6.29 MeV.

Question 13.13.
The radionuclide 116C decays according to
¹¹₆C → ¹¹₅B + e⁺ + v : T_1/2 = 20.3 min.
The maximum energy of the emitted positron is 0.960 MeV.
Given the mass values:
m(¹¹₆C) = 11.011434 u and
m(¹¹₆B) = 11.009305 u
Calculate Q and compare it with the maximum energy of the positron emitted.
Answer:
Given
¹¹₆C → ¹¹₅B+ e⁺ + v^- + Q, where Q is the kinetic energy released in the decay process. The Q of this decay process is given by
Q =    [m_N(¹¹₆C) - m_N(¹¹₅B) - m_e]c², the masses used in this equation are nuclear masses.
Now, if we express the Q value in terms of atomic masses we have to subtract 6 m_e from the atomic mass of carbon and 5 m_e from that of boron atomic to get the corresponding nuclear masses. Therefore, we have
Q = [m(¹¹C) - 6 m_e - m(¹¹B) + 5 m_e - m_e]c²
= [m(¹¹C) - m(¹¹B) - 2 m_e ]c²
= [11.011434 - 11.009305 - 2 x 0.000548] uc²
= (0.002129 - 0.001096) x 931.5 [∵ c² = 931 MeV/ u]
= 0.001033 x 931.5 = 0.961 MeV.

Question 13.14.
The nucleus ²³₁₀Ne decay by ß-emission. Write down ß-decay equation and determine the maximum kinetic energy of the electrons emitted. Given that :
m(²³₁₀Ne) = 22.994466 u,
m(²³₁₁Ne) = 22.989770 u, 
Answer:
²³₁₀Ne → [₁₁Na²³ + e^- + \bar{v}_e+ (Q)]
Q = [m_N (₁₀Ne²³) - m_N (₁₁Na²³) - m_e]c²
where the neutrino rest mass has been ignored.
Thus
Q = [m(²³₁₀Ne) - 10m_e - m(²³₁₁Na) + 11m_e - m_e]c²
= [22.994466 - 22.989770]c²
= [m(²³₁₀Ne) - m(²³₁₁Na)]c²
or Q = (22.994466 - 22.989770)uc²
= 0.004696 x 931.5 MeV
or Q = 4.374 MeV
This kinetic energy is mainly shared jointly by the \(e^{-}-\bar{v}\) pair since Na²³ is much more massive than this pair and its recoil energy is therefore negligible. The maximum energy of emission is equal to total kinetic energy of the \(e^{-}-\bar{v}_e\) pair. (When the electron has maximum kinetic energy, the neutrino carries no energy). Thus, the maximum kinetic energy of the ß emitted is 4.37 MeV.

Question 13.15.
The Q-value of a nuclear reaction A + b → C + d is defined by Q = [m_A + m_b - m_C - m_d] c² where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are all exothermic or endothermic:
(i) ¹₁H + ³₁H → ²₁H + ²₁H
(ii) ¹²₆C + ¹²₆C → ²⁰₁₀Ne + ⁴₂He atomic masses are given to be
m(²₁H) = 2.0141102 u, = 3.016049 u, m(¹²₆C) = 12.000000 u, m(²⁰₁₀Ne) = 19.992439 u,
Answer:
Substituting these values in the two equations, we get:
(i) Q = [m(₁H) + m(₁H)
= 2m (₁H)]c²
= (1.007825 + 3.016049 - 2.014102 - 2.014102) u
= (4.023874 - 2.014102 - 2.014102) u
= -0.00433 x 931.5 MeV
= -4.03 MeV
∴ reaction is endothermic

(ii) Q = [2m(₆C) - m(₁₀Ne) - m (₂He)]c²
= (12.000000 + 12.000000 - 19.992439 - 4.002603) u 
= 0.004958 x 931.5
= +4.62 MeV; reaction is exothermic.

Question 13.16.
Suppose, we think of fission of ⁵⁶₂₆Fe nucleus into two equal fragments, ²⁸₁₃Al. Is the fission energetically possible? Argue by working out Q of the process. Given m(⁵⁶₂₆Fe) = 55.93494 u and m(²⁸₁₃Al) = 27.98191 u.
Answer:
The reaction is:
⁵⁶₂₆Fe → ²⁸₁₃Al + ²⁸₁₃Al + Q
∴ Q = m(⁵⁶₂₆Fe) - 2m(²⁸₁₃Al)
= [55.93494 - 2 x 27.98191] u
= [55.93494 - 55.96382] u
= -0.02888 u
= -0.02888 x 931.5 MeV
= -26.9 MeV
Hence not possible.

Question 13.17.
The fission properties of ²³⁹₉₄Pu are very similar to those of ²³⁹₉₂U. The average energy released per fission is 180 MeV. How much energy in MeV is released if all the atoms in 1 kg of pure ²³⁹₉₄U undergo fission?
Answer:
Energy released per fission = 180 MeV
No.of atoms of 1 kg of ²³⁹₉₄Pu = \(\frac{6 \times 10^{23} \times 1000}{239}\)
∴ Energy released from the fission of 1 kg of ²³⁹₉₄Pu.
= 0.025 x 10²⁶ x 180
= 4.536 x 10²⁶ MeV.

Question 13.18.
A 1000 MW fission reactor consumes half of its fuel in 5.00 y. How much ²³⁵₉₂U did it contain initially? Assume that the reactor operates 80% of the time, that all the energy generated arises from the fission of ²³⁵₉₂U and that this nuclide is consumed by the fission process.
Answer:
Energy generated per gram of ²³⁵₉₂U
= \( \frac{6 \times 10^{23} \times 200 \times 1.6 \times 10^{-13}}{235}\) Jg-1
The amount of ²³⁵₉₂U consumed in 5 years with 80% in time.
= \(\frac{5 \times 0.8 \times 365 \times 24 \times 6 \times 6 \times 10^{11}}{6 \times 2 \times 1.6 \times 10^{12}}\) x 235 g
= 1544.15 x 10³ g
= 1544.15 kg.
The initial amount of ²³⁵₉₂U= 1544.15 x 2
= 3088.3 kg.

Question 13.19.
How long an electric lamp of 100 W can be kept glowing by fusion of 2.0 kg of deuterium? The fusion reaction as
²₁H + ₂₁H → ³₂He + n + 3.27 MeV
Answer:
Number of deuterium atoms in 2 kg
= \(\frac{6.023 \times 10^{23}}{2}\) x 2000 = 6.023 x 10²⁶
Energy released when 6.023 x 10²³ nuclei of deuterium fuse together
= \(\frac{3.2}{2}\) x 6.023 x 10²⁶ MeV
= \(\frac{3.2 \times 6.023 \times 10^{26}}{2}\) x 1.6 x 10^-13 J
= 15.76 x 10¹³ J
Power of lamp = 100 W
If the lamp glows for time t, then electric energy consumed = 100 t
∴ 100 t = 15.76 x 10³³
∴ t = 0.1576 x 10¹³ s
= \(\frac{0.1576 \times 10^{13}}{365 \times 86400}\) y
or t ≈ 4.99 x 10⁴ y.

Question 13.20.
Calculate the height of the potential barrier for head-on collision of two deuterons, (Hint: The height of the potential barrier if given by the Coulomb repulsion between the two deuterons when they just touch each other.) Assume that they can be taken as hard spheres of radius 2.0 fm.
Answer:
Radius of deuteron r = 2.0 fm
= 2 x 10^-15 m
Initial energy of two deuterons = 2KE
This energy is converted into PE, after the head-on collision, when deuteron stops and is given by
U = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{e^2}{2 r}\)
From law of conservation of energy, we have

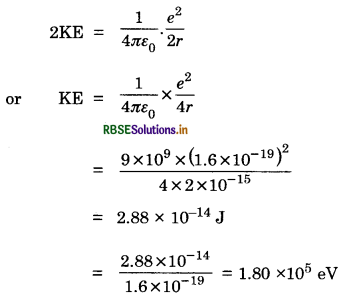
= 180 keV
PE = 2K.E. = 180 x 2 = 360 keV.

Question 13.21.
From the relation R = R₀A^1/3, where R₀ is a constant and A is the mass number of a nucleus. Show that the nuclear matter density is nearly constant (i.e. independent of A).
Answer:
Density of necleus (ρ). It is defined as the nuclear mass per unit volume.

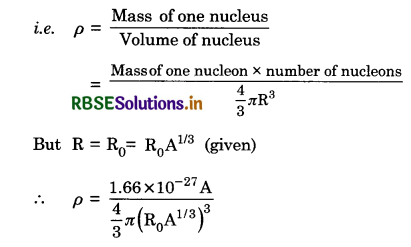
or ρ = \(\frac{3 \times 1.66 \times 10^{-27} \mathrm{~A}}{4 \times 3.142 \times\left(1.2 \times 10^{-15}\right)^3 \times \mathrm{A}}\)
= 2.29 x 10¹⁷ kg m^-3.
Thus the nuclear density is of the order of 10¹⁷ kg m^-3 and is independent of its mass number. Therefore, all nuclei have the same approximate density.

Question 13.22.
For the ß⁺ (positron) emission from a nucleus, there is another competing process known as electron capture (electron from an inner orbit, say the K-shell) is captured by the nucleus and a neutrino is emitted:
e + _ZX^A → _Z-1Y^A + v
Show that if ß⁺ emission is energetically allowed, electron capture is necessarily allowed but not vice versa,
Answer:
Consider the two competing processes:
(i) Case of positron emission
^A_ZX → ^A_z-1Y + e⁺ + Q₁ (positron emission)
Q₁ = [m_N(^A_ZX) = m_N(_Z-1Y^A) - m_e]c²
= [m(^A_ZX) - Zm_e - m(_Z-1^AY) - (Z-1)m_e - m_e]c²
= [m(^A_ZX) - m(^A_Z-1Y) - 2m_e]c²

(ii) Case of electron capture
e^- + _ZX^A → _Z-1Y^A + v_e + Q₂ (electron capture)
Q₂ = [m_N(^A_ZX) + m_e - m_N(_Z-1^AY)]c²
= [m(^A_ZX) -m(^A_Z-1Y]c²
From eqns. Q₂ > Q₁
If Q₁ > 0, Q₂ will necessarily be more than zero. It means that if positron emission allowed e^- capture will necessary be allowed.
But if Q₂ > 0, Q₁ may not be more than zero. It means that if e^- capture is allowed positron emission may not be allowed.

ADDITIONAL EXERCISES

Question 13.23.
In a periodic table atomic mass of magnesium is given as 24.312 u. The average value is based on their natureal abundance on Earth. The three isotopes and their mases are ²⁴₁₂Mg (23.98504 u), ²⁵₁₂Mg (24.98584 u) and ²⁶₁₂Mg (25.98259 u). The natural abundance of ²⁴₁₂Mg is 78.99% by mass. Calculate the abundances of the other two isotopes.
Answer:
Atomic mass of ²⁴₁₂Mg = 23.98504 u
Atomic mass of ²⁵₁₂Mg = 24.98584 u
Natural abundance of ²⁴₁₂Mg = 78.99
Let natural abundance of ²⁴₁₂Mg = x (say)
Atomic mass of ²⁶₁₂Mg = 25.98259 u
Natural abundance of ²⁶₁₂Mg
= [100 - (78.99 + x)] = 21.01 - x
Average atomic mass of magnesium
= 24.312 u .............(i)
∴ Average atomic mass from the given data.
\(\frac{78.99 \times 23.98504+24.98584 \times x+(21.01-x) 25.98254}{100}\) u .....................(ii)
From (i) and (ii)
24.312 = \(\frac{-25.98254 x}{100}\)
or 0.99625 x = 9.27
or x = \(\frac{9.27}{0.99675}\) = 9.30
So 21.01 - x = 21.01 - 9.30 = 11.71.
Hence relative abundance of 2512Mg
= 9.3%
and that of ²⁶₁₂Mg = 11.7%.

Question 13.24.
The neutron separation energy is defined to be the energy required to remove a neutron from a nucleus. Obtain the neutron separation energies of the nuclei ⁴¹₂₀Ca and ²⁷₁₃Al from the following data:
m(⁴⁰₂₀Ca) = 39.962591 u,
m(⁴¹₂₀Ca) = 40.962278 u,
m(₁₃²⁶Al) = 25.986895 u,
m(²⁷₁₃Al) = 26.981541 u,
Answer:
Neutron separation energy S_n of a nucleus ^A_XX is given by
S_n = [m_N(^A-1_ZX) + m_n -m_N(^A_ZX)]c²
Adding and subtracting the term Zm_C in the bracket above ignoring mass defects due to electronic binding energies we get S_n in terms of atomic masses.
S_n = [m_N(^A-1_ZX) + m_n - m(^A_ZX)]c²
Sn(4120X) = [(39.96259 + 1.008665 - 40.962278)]u,
= [40.971255 - 40.962278] 931.5
= 0.008978 x 931.5
= 8.363 MeV.
Neutron separation energy for ²⁷₁₃Al
Sn (²⁷₁₃Al) = [m_N(²⁶₁₃Al) + m_n - m_N(²⁷₁₃Al)]c²
Sn (²⁷₁₃Al) = [25.986895 + 1.0008665 - 26.981541] u
= [26.99556 - 26.981541] 931.5
= 0.014019 x 931.5
= 13.06 MeV.

Question 13.25.
A source contains two phosphorus radio nuclides ³²₁₅P (T_1/2 = 14.3 d) and ³³₁₅P (T_1/2 = 25.3 d). Initially, 10% of the decays come from ³³₁₅P. How long one must wait until 90% do so?
Answer:
Let R₀₁ and R₀₂ be initial activities of ³³₁₅P and ³²₁₅P respectively.
Let R₁ and R₂ be activities at time t, then
Total initial activity = R₀₁ + R₀₂
Total activity at time t = R₁ + R₂
Given R₀₁ = 10% of total activity

λ₁ = \(\frac{0.693}{25.3}\)day^-1
So Eq.(4) becomes
\(\left[\frac{0.693}{14.3}-\frac{0.693}{25.3}\right]\) t = 2.303 log 81
or t = 2.303 x 1.9085\(\frac{25.3 \times 14.3}{0.693(25.3-14.3)}\)
or t = 208.6 days.

Question 13.26.
(a) Under certain circumstances, a nucleus can decay by emitting a particle more massive than an α-particle. Consider the following decay processes:
²²³₈₈Ra → ²⁰⁹₈₂Pb + ¹⁴₆C
²²³₈₈Ra → ²¹⁹₈₆Rn + ⁴₂He
(b) Calculate the Q-values for these decays and determine that both are energetically allowed.
Answer:
(a) For the decay process
²²³₈₈Ra → ²⁰⁹₈₂Pb + ¹⁴₆C + Q
Q = [m_N(²²³₈₂Ra) - m_N(²⁰⁹₈₂Pb) - m_N(¹⁴₆C)]c²
= [m(²²³₈₈Ra) - m(²⁰⁹₈₂Pb) - m (¹⁴₆C)]c²
= [223.01850 - 208.98107 - 14.00324] uc²
or Q = [0.03419]uc²
= 0.03419 x 931.5 MeV
= 31.85 MeV
For the decay process
²²³₈₈Ra → ²¹⁹₈₆Rn + ⁴₂He + Q
Q = [m_N(²²³₈₈Ra) - m_N(²¹⁹₈₆Rn) - m_N(⁴₂He)]c²
= [m(²²³₈₈Ra) - m( ²¹⁹₈₆Rn ) - m (⁴₂He)] c²
= (223.01850 - 219.00948 - 4.00260) uc²
= (0.00642) uc²
= 0.0642 x 931.5 MeV
= 5.98 MeV.

Question 13.27.
Consider the fission of ²³⁸₉₂U by fast neutrons. In one fission event, no neutrons are emitted and the final stable end products, after the beta-decay of the primary fragments, are¹⁴⁰₅₈Ce and ⁹⁹₄₄Ru. Calculate Q for this fission process. The relevant atomic particle masses are
m(²³⁸₉₂U) = 238.05079 u, 
m(¹⁴⁰₅₈Ce) = 139.90543 u,
m(⁹⁹₄₄Ru) = 98.90594 u,
mn = 1.00867 u
Answer:
For the fission
²³⁸₉₂U + ¹₀n → ¹⁴⁰₅₈Ce + ⁹⁹₄₄Ru + Q
Q = [m_N (²³⁸₉₂U) + m_N - m(¹⁴⁰₅₈Ce) - m(⁹⁹₄₄Ru)]c²
= [m(²³⁸₉₂U) + m_N - m(¹⁴⁰₅₈Ce) - m(⁹⁹₄₄Ru)]c²
= [238.05079+1.00867 - 139.90543 - 98.90594] uc²
= [239.05946 -238.81137] uc²
= (0.24809) x 931.5 MeV
= (231.1) MeV.

Question 13.28.
Consider the D - T reaction (deuterium-tritium fusion)
²₁H + ³₁H → ⁴₂He + n
(a) Calculate the energy released in MeV in this reaction from the data:
m(²₁H)= 2.014102 u
m(³₁H) = 3.016049 u
(b) Consider the radius of both deuterium and tritium to be approximately 2.0 fm. What is the kinetic energy needed to overcome the coulomb repulsion between the two nuclei? To what temperature must the gas be heated to initiate the reaction?
(Hint: Kinetic energy required for one fusion event = average Thermal kinetic energy available with the interacting particles = 2(\(\frac{3}{2}\)KT):
k = Boltzmann’s constant,
T = absolute temperature?
Answer:
(a) The given equation is:
²₁H+ ³₁H → ⁴₂He + ¹₀n + Q
So energy released in this reaction:
Q = [m_N(²₁H) + m_N(³₁H) - m(⁴₂He) +m_N]c²
= [{m(²₁H) - m_e} + {m(³₁H) - m_e} -{m(⁴₂He) - m_n}]
= [{m(²₁H) + m(³₁H)} - m(⁴₂He) - m_n]c²
= [2.0114102 + 3.016049 - 4.002603 - 1.008665] uc²
= 0.018883 x 931.5 MeV
= 17.59 MeV

(b) Repulsive potential energy of two approaching nuclei when they are the nearest to each other (r₀) is: 
PE = \(\frac{1}{4 \pi \varepsilon_0} \times \frac{e^2}{r_0}\)
where r₀ = 2r = 2 x 2.0 x 10^-15 m
= 4 x 10^-15 m
So PE = \(\frac{9 \times 10^9\left(1.6 \times 10^{-19}\right)^2}{4.0 \times 10^{-15}}\) J
= 5.76 x 10^-14 J
K.E. required to overcome coulomb repulsion
= P.E.
So K.E. = 7.68 x 10^-14 J
Since K.E. = 3 kT
∴ T = \(\frac{\mathrm{K} . E .}{3 k}=\frac{5.76 \times 10^{-14}}{3 \times 1.38 \times 10^{-23}}\)
= 1.391 x 10⁹ K.

Question 13.29.
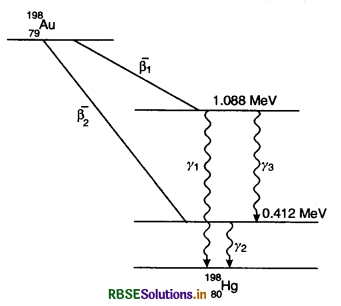
Obtain the maximum kinetic energy of ß-particles, and the radiation frequencies of γ-decays in the following decay scheme. You are given that:
m(₇₉Au¹⁹⁸) = 197.968233 u
m(₈₀Hg¹⁹⁸) = 197.966760 u.

Answer:
Beta decay equation for 79Au198 is
₇₉ Au¹⁹⁸ → ₈₀Hg¹⁹⁸ + _-1e⁰ + \(\overline{\boldsymbol{\nu}}\) + Q
But Q = [M' (₇₉Au¹⁹⁸) - {M' (₈₀Hg¹⁹⁸) + me}]c²
(Ignoring rest mass of antineutrino(\(\overline{\boldsymbol{\nu}})\)
where M' present mass of the nuclei.
Adding and subtracting mass 79m_e of 79 electrons
Q = [{M' (₇₉AU¹⁹⁸) + 97m_e} - M' (₈₀Hg¹⁹⁸) + 79m_e + m_e}] c²
= {[M (₇₉Au¹⁹⁸) - M (₈₀Hg¹⁹⁸] c²
where M represent mass of atoms
Hence, K.E. of particles
Q = [M(₇₉Au¹⁹⁸) - M(₈₀Hg¹⁹⁸)c²
= (197.968233 - 197.966760)] u
= 0.001473 u
or Q = 0.001473 x 931.5 MeV
= 1.3721 MeV

In ß^-₁ transition. K.E. shared by
₈₀Hg¹⁹⁸ = 1.088 MeV (Fig. 13.1)
Max K.E. of ß₁ particle
= 1.3721 - 1.088
= 0.2841 MeV

In ß^-₂ transition, K.E. shared by
₈₀Hg¹⁹⁸ = 0.412 MeV (Fig. 13.1)
Max K.E. of ß₂ particle
= 1.3721 - 0.412
= 0.9601 MeV

For γ₁, energy
hv = 1.088 MeV
= 1.008 x 1.6 x 10^-13 J
Frequency,
V = \(\frac{h v}{h}\)
= \(\frac{1.088 \times 1.6 \times 10^{-13}}{6.626 \times 10^{-34}}\)
= 2.6273 x 10²⁰ Hz.

or γ₂ energy,
hv = 0.412 MeV
= 0.412 x 1.6 x 10^-13 J
Frequency,
V = \(\frac{h v}{h}=\frac{0.412 \times 1.6 \times 10^{-13}}{6.626 \times 10^{-34}}\)
= 0.99488 x 10²⁰ Hz

For γ₃
v(γ₃) = v(γ₁) - v(γ₂)
= 2.62730 x 10²⁰ - 0.99488 x 10²⁰
= 1.63242 x 10²⁰ Hz

For γ₂ energy
hv = 0.412 MeV
= 0.412 x 1.6 x 10^-13 J.

Question 13.30.
Calculate and compare energy released by
(а) fusion of 1.0 kg of hydrogen deep within the sun and
(b) the fission of 1.0 kg of ²³⁵₉₂U in a fission reactor.
Answer:
(a) In Sun, 4 hydrogen nuclei combine to form a helium nucleus with a release of ~26 MeV of energy.
The energy released by fusion of 1 kg of hydrogen.
= \(\frac{6 \times 10^{23} \times 26}{4}\) x 10³ MeV
= 39 x 10²⁵ MeV

(b) Energy released in fission of one atom of
²³⁵₃₅U = 200 MeV
Energy released in fission of 1 kg of
²³⁵₉₂U = \(\frac{6 \times 10^{23} \times 200}{235}\) x 1000 MeV
= 5.1 x 10²⁶ MeV
Thus the energy released in fusion of 1 kg of hydrogen is about 8 times \(\left(\frac{39.13 \times 10^{26}}{5.1 \times 10^{26}}=7.6 \simeq 8\right)\) that of the energy released in the fusion of 1 kg of uranium.

Question 13.31.
Suppose India has a target of producing by 2020 A.D. 200,000 MW of electric power, ten percent of which was to be obtained from nuclear power plants. Suppose we are given that, an average the efficiency of utilization (i.e. conversion to electric energy) of thermal energy produced in a reactor is 25%. How much amount of fissionable uranium would our country need per year by 2020? Take the heat energy per fission ²³⁵U to be about 200 MeV.
Answer:
Required power from nuclear plants
= 2 x 10¹¹ x \(\frac{10}{100}\) = 2 x 10¹⁰ W
Required electric energy from nuclear plant in one year
= 2 x 10¹⁰ x 365.25 x 24 x 60 x 60
= 6.312 x 10¹⁷ J.
Available electric energy per fission
= 25 x 200 M eV = 8 x 10^-12
Energy released per energy per fission = 200 MeV
Energy available per fission
= \(\frac{25}{100}\) x 200 = 50 MeV
= 50 x 1.6 x 10^-13 = 8 x 10^-12 J
Required no.of fission per year
= \(\frac{6.312 \times 10^{17}}{8 \times 10^{-12}}\) = 7.89 x 10²⁸
Mass of 6.023 x 10²³ atoms of ²³⁵₉₂U
= 235 g = 235 x 10^-3 kg
So required mass of ²³⁵₉₂U to produce 7.89 x 10²⁸ nuclei
= \(\frac{235 \times 10^{-3}}{2.023 \times 10^{23}}\) x 7.89 x 10²⁸
= 3.076 x 10⁴ kg.

SELECTED EXEMPLAR PROBLEMS

MCQ I. (with one correct option)

Question 13.1.
Suppose we consider a large number of containers each containing initially 10000 atoms of a radioactive material with a half life of 1 year. After 1 year
(а) all the containers will have 5000 atoms of the material.
(b) all the containers will contain the same number of atoms of the material but that number will only be approximately 5000.
(c) the containers will in general have different numbers of the atoms of the material but their average will be close to 5000.
(d) none of the containers can have more than 5000 atoms.
Answer:
(c) After one year, on the average, half of the atoms will decay, so the containers will in general have different number of atoms of the material but their average will be close to 5000.
 
Question 13.2.
The gravitational force between a H-atom and another particle of mass m will be given by Newton’s law:
F = \(\mathrm{G} \frac{\text { M.m }}{r^2}\), where r is in km and
(а) M = m_proton + m_electron.
(b) M = m_proton + m_electron - \(\frac{\mathbf{B}}{c^2}\) (B = 13.6 eV).
(c) M is not related to the mass of the hydrogen atom.
(d) M = m_proton + m_electron -\(\frac{|\mathbf{V}|}{c^2}\) (|V| = magnitude of the potential energy of electron in the H-atom).
Answer:
(b) M = m_proton + m_electron - \(\frac{\mathbf{B}}{c^2}\) (B = 13.6 eV)

Question 13.3.
When a nucleus in an atom undergoes a radioactive decay, the electronic energy levels of the atom
(а) do not change for any type of radioactivity.
(b) change for α and ß radioactivity but not for γ-radioactivity.
(c) change for α-radioactivity but not for others.
(d) change for ß-radioactivity but not for others.
Answer:
(b) Since γ-rays has no charge, so there is no change of γ-radioactivity.

Question 13.4.
Mx and My denote the atomic masses of the parent and the daughter nuclei respectively in a radioactive decay. The Q-value for a ß⁺ decay is Q₁ and that for a ß⁺ decay is Q₂. If me denotes the mass of an electron, then which of the following statements is correct?
(a) Q₁ = (M_x - M_y) c² and Q₂ = (M_x - M_y - 2 m_e)c²
(b) Q₁ = (M_x - M_y) c² and Q₂ = (M_x - M_y) c²
(c) Q₁ = (M_x - M_y - 2 m_e) c² and Q₂ = (M_x - M_y + 2 m_e) c²
(d) Q₁ = (M_x - M_y + 2 m_e) c² and Q₂ = (M_x - M_y + 2 m_e) c²
Answer:
(a) For ß^- decay Q₁ = (M_x - M_y) c²
For ß+ decay Q₂ = (M_x - M_y - 2 m_e) c²

Question 13.5.
Tritium is an isotope of hydrogen whose nucleus Triton contains 2 neutrons and 1 proton. Free neutrons decay into p + \(\overline{\boldsymbol{e}} + \overline{\boldsymbol{v}}\). If one of the neutrons in Triton decays. It would transform into He³ nucleus. This does not happen. This is because
(а) triton energy is less than that of a He³ nucleus.
(b) the electron created in the beta decay process cannot remain in the nucleus.
(c) both the neutrons in triton have to decay simultaneously resulting in a nucleus with 3 protons, which is not a He³ nucleus.
(d) because free neutrons decay due to external perturbations which is absent in a triton nucleus.
Answer:
(a) Triton energy is less than that of a He³ nucleus.

Question 13.6.
Heavy stable nuclei have more neutrons than protons. This is because of the fact that
(a) neutrons are heavier than protons.
(b) electrostatic force between protons are repulsive.
(c) neutrons decay into protons through beta decay.
(d) nuclear forces between neutrons are weaker than that between protons.
Answer:
(b) The electrostatic force between protons are repulsive, which may reduce stability.

Question 13.7.
In a nuclear reactor, moderators slow down the neutrons which come out in a fission process. The moderator used have light nuclei. Heavy nuclei will not serve the purpose because
(a) they will break up
(b) elastic collision of neutrons with heavy nuclei will not slow them down.
(c) the net weight of the reactor would be unbearably high.
(d) substances with heavy nuclei do not occur in liquid or gaseous state at room temperature.
Answer:
(b) In elastic collision, the velocities are exchanged. Heavy nuclei will serve the purpose as elastic collisions of neutrons with heavy nuclei will not slow down.

MCQ II. (with more than one correct options)

Question 13.8.
Fusion processes, like combining two deuterons to form a He nucleus are impossible at ordinary temperatures and pressure. The reasons for this can be traced to the fact:
(а) nuclear forces have short range.
(b) nuclei are positively charged.
(c) the original nuclei must be completely ionized before fusion can take place.
(d) the original nuclei must first break up before combining with each other.
Answer:
(a), (b) The reason is that nuclear forces are short range forces and nuclei are positively charged.

Question 13.9.
Samples of two radioactive nuclides A and B are taken. λ_A and λ_B are the disintegration constants of A and B respectively. In which of the following cases, the two samples can simultaneously have the same decay rate at any time?
(a) Initial rate of decay of A is twice the initial rate of decay of B and λ_A = λ_B.
(b) Initial rate of decay of A is twice the initial rate of decay of B and λ_A > λ_B.
(c) Initial rate of decay of B is twice the initial rate of decay of A and λ_A > λ_B.
(d) Initial rate of decay of B is the same as the rate of decay of A at t = 2h and λ_B < λ_A.
Answer:
(b), (d) The two samples can simultaneously have the same decay rate, if initial rate of decay of A is twice the initial rate of decay of and also when initial rate of decay of B is same as the rate of A at t = h and λ_B < λ_A.

Question 13.10.
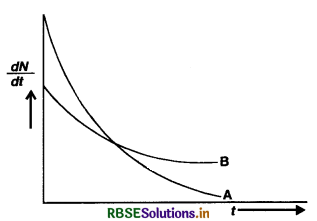
The variation of decay rate of two radioactive samples A and B with time is shown in Fig. 13.2.
Which of the following statements are true?
(а) Decay constant of A is greater than that of B, hence A always decays faster than B.
(b) Decay constant of B is greater than that of A but its decay rate is always smaller than that of A.
(c) Decay constant of A is greater than that of B but it does not always decay faster than B.
(d) Decay constant of B is smaller than that of A but still its decay rate becomes equal to that of A at a later instant.

Answer:
(c), (d) Rate of decay \(\frac{d \mathrm{~N}}{d t}\) ∝ λ, so here λ_A > λ_B. At point of intersection of two curves decay of both is the same.

Very Short Answer Type Questions

Question 13.11.
₂He³ and ₁H³ nuclei have the same mass number. Do they have the same binding energy?
Answer:
No. As ₁He³ has one proton and 2 neutrons, so there is no repulsive force [₂He³ has two protons and one neutron), so the B.E. of ₁H³ > ₂He³.

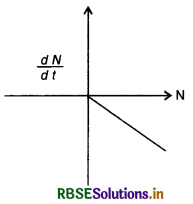
Question 13.12.
Draw a graph showing the variation of decay rate with number of active nuclei.
Answer:
Since -\(\frac{d \mathrm{~N}}{d t}\) = λ_N. So graph between \(\frac{d \mathrm{~N}}{d t}\) and N is as shown in the figure EP 13.12.

Question 13.13.
Which sample, A or B shown in Fig. EP 13.13 has shorter mean life?

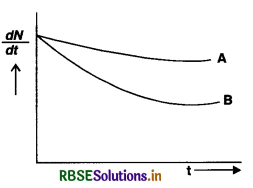
Answer:
At t = 0, (N₀)_A = (N₀)_B
At any later time
\(\left(\frac{d \mathrm{~N}}{d t}\right)_{\mathrm{A}}>\left(\frac{d \mathrm{~N}}{d t}\right)_{\mathrm{B}}\)
or λ_A N_A > λ_B N_B
As N_A > N_B (Decay rate of B is slower)
∴ λ_B > λ_A.

Question 13.14.
Which one the following cannot emit radiation and why?
Excited nucleus, excited electron.
Answer:
Excited nucleus emit radiation but excited electron cannot, because the energy of electronic levels is in the range of eV and energy of γ-rays is in MeV range.

Question 13.15.
In pair annihilation, an electron and a positron destroy each other to produce gamma radiation. How is the momentum conserved?
Answer:
In pair annihilation of an electron and proton, two γ-rays are produced and they move in opposite directrons to conserve momentum.

Short Answer Type Questions

Question 13.16.
Why do stable nuclei never have more protons than neutrons?
Answer:
Because protons are positively charged particles and they exert force of repulsion and this repulsion becomes so great in nuclei with N_p = 10, so an excess of neutrons which produces only attractive forces, is required for stability.

Question 13.17.
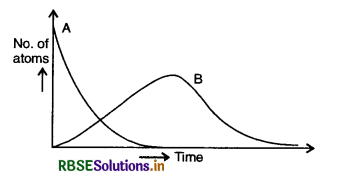
Consider a radioactive nucleus A which decays to a stable nucleus C through the following sequence:
A → B → C
Here B is an intermediate nucleus which is also radioactive. Considering that there are N₀ atoms of A initially, plot the graph showing the variation of number of atoms of A and B versus time.
Answer:
Given that the radioactive decays of A to stable nucleus C is through the sequence
A → B → C
At t = 0, N_A = N₀ and N_B = 0. As time increases, N_A falls off exponentially, the number of atoms of B increases, becomes maximum and finally decay to zero at ∞ as shown in the given figure EP 13.17.

Question 13.18.
A piece of wood from the ruins of an ancient building was found to have a ¹⁴C activity of 12 disintegrations per minute per gram of its carbon content. The ¹⁴C activity of the living wood is 16 disintegrations per minute per gram. How long ago did the tree, from which the wooden sample came, die? Given half-life of ¹⁴C is 5760 years.
Answer:
Given T = 5760 years, t - ?, R₀ = 16 disintegration per min per gram, R = 12 disintegration per min per gram

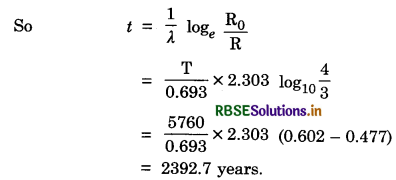
Question 13.19.
Are the nucleons fundamental particles, or do they consist of still smaller parts? One way to find out is to probe a nucleon just as Rutherford probed an atom. What should be the kinetic energy of an electron for it to be able to probe a nucleon? Assume the diameter of a nucleon to be approximately 10^-15 m.
Answer:
Yes, nucleons are fundamental particles.
To resolve two objects separated by distance d, the wavelength λ of the proving signal must be less than d.
So to detect separate parts inside a nucleon the electron must have a wavelength less than 10^-15 m.
And KE = pc = \(\frac{h c}{\lambda}=\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{1.6 \times 10^{-19} \times 10^{-15}}\) eV
or K = 10⁹ eV = 1 GeV.

Question 13.20.
A nuclide 1 is said to be the mirror isobar of nuclide 2 if Z₁ = N₂ and Z₂ = N₁.
(a) What nuclide is a mirror isobar of ²³₁₄Na?
(b) Which nuclide out of the two mirror isobars have greater binding energy and why?
Answer:
(a) ₁₁N²³ : Z₁ = 11, N₁ = 12
₁₂Mg²³ : Z₁ = 12, N₂ = 11
∴ Mirror isobar of ₁₁Na²³ = ₁₂Mg²³.
(b) Since Z₂ > Z₁ so Mg has greater binding energy than Na.

Long Answer Type Questions

Question 13.21.
Deuteron is a bound state of a neutron and a proton with a binding energy B = 2.2 MeV. A γ-ray of energy E is aimed at a deuteron nucleus to try to break it into a (neutron + proton) such that the n and p move in the direction of the incident γ-ray. If E = B, show that this cannot happen. Hence calculate how much bigger than B must E be for such a process to happen.
Answer:
From law of conservation of energy
E - B = K_n + K_p = \(\frac{p_n^2}{2 m}+\frac{p_p^2}{2 m}\) ...................(i)
From law of conservation of momentum 
p_n + p_p = \(\frac{\mathrm{E}}{c}\)  .......................(ii)
If E = B, Eq. (i) gives
p_n = p_p = 0 and hence Eq. (ii) cannot be satisfied and the process cannot take place
For the process to take place Let E = B + λ (λ << B)
Putting the value of p_n from Eq. (ii) in Eq. (i), we get

For p_p to be real

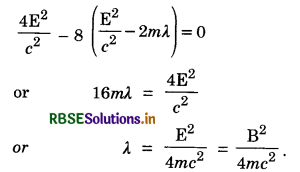
Question 13.22.
Before the neutrino hypothesis, the beta decay process was thought to be the transition n → p + \(\bar{e}\)
If this was true, show that if the neutron was at rest, the proton and electron would emerge with fixed energies and calculate them. Experimentally, the electron energy was found to have a large range.
Answer:
Before ß-decay, neutron is at rest. Hence E_n = m_nc², p_n = 0

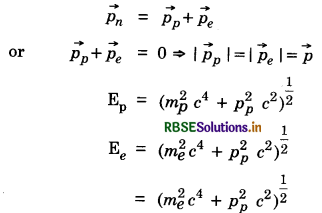
From conservation of energy
\(\left(m_p^2 c^4+p^2 c^2\right)^{\frac{1}{2}}+=\left(m_e^2 c^4+p^2 c^2\right)^{\frac{1}{2}}=m_n c^2\)
m_p c² = 936 MeV, m_n c² = 938 MeV, m_e c² = 0.51 MeV
Since, the energy difference between n and p is small, pc will be small, pc << m_p c², pc may be greater than m_ec²
m_pc² + \frac{p^2 c^2}{2 m_e^2 c^4} = m_nc² - pc
To first order pc = mⁿ c² - m_p c²
= 938 MeV - 936 MeV = 2 MeV
This gives the momentum of proton or neutron.
Then

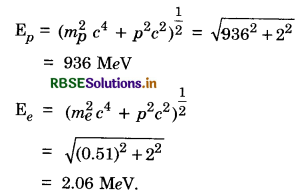
Question 13.23.
Nuclei with magic no. of proton Z = 2, 8, 20, 28, 50, 52 and magic no. of neutrons N = 2, 8, 20, 28, 50, 82 and 126 are found to be very stable, (i) Verify this by calculating the proton separation energy S_p for ¹²⁰Sn (Z = 50) and ¹²¹Sb = (Z = 51). The proton separation energy for a nuclide is the minimum energy required to separate the least tightly bound proton from a nucleus of that nuclide. It is given by
S_p = (M_z-1,N + M_H - M_{z, N})c².
Given ¹¹⁹ln = 118.9058u, ¹²⁰Sn = 119.902199u, ¹²¹Sb = 120.903824u, ¹H = 1.0078252u.
(ii) What does the existence of magic number indicate?
Answer:
(i) Proton separation is given by
S_pSn = (M_119.70 + M_H - M_120.70)c²
= (118.9058 + 1.0078252 - 119.902199)c²
= 0.0114362c²
S_pSb = (M_120.70 + M_H - M_121.70)c²
= (119.902199 + 1.0078252 + 120.903822)c²
= 0.0059912c²
Since S_pSn > S_pSb Sn nucleus is more stable than Sb nucleus.

(ii) It indicates shell structure of nucleus similar to the shell structure of an atom. This also explains the peaks in BE/nucleon curve.