RBSE Solutions for Class 12 Physics Chapter 12 परमाणु

Rajasthan Board RBSE Solutions for Class 12 Physics Chapter 12 परमाणु Textbook Exercise Questions and Answers.

RBSE Class 12 Physics Solutions Chapter 12 परमाणु

RBSE Class 12 Physics परमाणु Textbook Questions and Answers

प्रश्न 1. 
प्रत्येक कथन के अन्त में दिये गये संकेतों से सही विकल्प का चयन कीजिए
(a) थॉमसन मॉडल में परमाणु का साइज, रदरफोर्ड मॉडल में परमाण्वीय साइज से .................... होता है। (अपेक्षाकृत काफी अधिक, भिन्न नाहीं, अपेक्षाकृत काफी कम)
(b) .................. में निम्नतम अवस्था में इलेक्ट्रॉन स्थायी साम्य में होते हैं जबकि ................... में इलेक्ट्रॉन, सदैव नेट बल अनुभव करते हैं। (रदरफोर्ड मॉडल, थॉमसन मॉडल)
(c) .................... पर आधारित किसी क्लासिकी परमाणु का नष्ट होना निश्चित है। (थॉमसन मॉडल, रदरफोर्ड मोडल)
(d) किसी परमाणु के द्रव्यमान का ................................ में लगभग सतत वितरण (continuous distribution) होता है लेकिन ........................... में अत्यन्त असमान द्रव्यमान वितरण होता है। (रदरफोर्ड मॉडल, थॉमसन मॉडल) 
(e) .......................... में परमाणु के अनावेशित भाग का द्रव्यमान सर्वाधिक होता है। (रदरफोर्ड मॉडल, दोनों मॉडलों) 
उत्तर:
(a) भिन्न नहीं
(b) थॉमसन मॉडल, रदरफोर्ड मॉडल
(c) रदरफोर्ड मॉडल
(d) थॉमसन मॉडल, रदरफोर्ड मॉडल
(e) रदरफोर्ड

प्रश्न 2. 
मान लीजिए कि स्वर्ण पन्नी के स्थान पर ठोस हाइड्रोजन की पतली शीट (thin sheet) का उपयोग करके आपको α - कण प्रकीर्णन प्रयोग का अवसर प्राप्त होता है। (हाइड्रोजन 14 K से नीचे ताप पर ठोस हो जाती है।) आप किस परिणाम की अपेक्षा करते हैं (what result do you expect)?
उत्तर:
हाइड्रोजन परमाणु का नाभिक एक प्रोटॉन है जिसका द्रव्यमान (1.67 x 10^-27 kg) α - कण के द्रव्यमान (6.64 x 10^-27 kg) की तुलना में कम (लगभग एक चौथाई) है, अत: यह हल्का नाभिक α - कण को प्रतिक्षिप्त नहीं कर पायेगा। फलस्वरूप व कण सीधे नाभिक की ओर जाने पर भी वापस नहीं लौटेगा। इसके साथ - साथ इस प्रयोग में α - कण का बड़े प्रकीर्णन कोणों पर विक्षेपण भी नहीं होगा।

प्रश्न 3. 
'पाश्चन श्रेणी' में विद्यमान स्पेक्ट्रमी रेखाओं की लघुत्तम तरंगदैर्घ्य (shortest wevelength) क्या है?
उत्तर:
पाश्चन श्रेणी की लघुत्तम तरंगदैर्य के लिए
n₁ = 3, n₂ = ∝
∴\( \frac{1}{\lambda_s}=\mathrm{R}\left[\frac{1}{3^2}-\frac{1}{\infty}\right]=\frac{\mathrm{R}}{9}\)
⇒ \({\lambda_s}=\frac{9}{\mathrm{R}}=\frac{9}{1097 \times 10^7}\)
= 8.2041 x 10^-17 m
= 8204.1 Å

प्रश्न 4.
2.3 eV ऊर्जा अन्तर किसी परमाणु में दो ऊर्जा स्तरों को पृथक् कर देता है। उत्सर्जित विकिरण की आवृत्ति क्या होगी यदि परमाणु में इलेक्ट्रॉन उच्च स्तर से निम्न स्तर में संक्रमण करता है?
हल: 
दिया है ∆E = -2.3 eV = 2.3 x 1.6 x 10^-19 J
h = 6.62 x 10^-34 Js, v = ? 
बोहर के तृतीय अभिगृहीत से,
∆E = hv ⇒ v = \(\frac{\Delta \mathrm{E}}{h}\)
\(v=\frac{2.3 \times 1.6 \times 10^{-19}}{6.62 \times 10^{-34}}\)
= 5.6 x 10¹⁴ Hz

प्रश्न 5. 
हाइड्रोजन परमाणु की निम्नतम अवस्था (ground state energy) में ऊर्जा - 13.6 eV है। इस अवस्था में इलेक्ट्रॉन की गतिज और स्थितिज ऊर्जाएँ क्या होंगी?
हल: 
कुल कर्जा ET = -13.6 eV 
गतिज कर्जा (K) = -ET = (-13.6)
= 13.6 eV
स्थितिज ऊर्जा = -2K = -2 x 13.6 
= - 27.2 eV प्रश्न 6. 
निम्नतम अवस्था में विद्यमान एक हाइड्रोजन परमाणु एक फोटॉन को अवशोषित (absorbs) करता है जो इसे n = 4 स्तर तक उत्तेजित कर देता है। फोटॉन की तरंगदैर्ध्य तथा आवृत्ति ज्ञात कीजिए।
हल: 
हाइड्रोजन परमाणु की गयीं कक्षा की ऊर्जा
\(\mathrm{E}_n=-\frac{13 \cdot 6}{n^2} \mathrm{eV}\)
n = 1 के लिए E₁ = -13.6 eV
n = 4 के लिए, E₄ = \(-\frac{136}{(4)^2}=-\frac{136}{16}\)
= -0.85 eV
∴ n= 1 से n = 4 तक उत्तेजित करने वाले फोटॉन की ऊर्जा
\(\Delta \mathrm{E}=\mathrm{E}_4-\mathrm{E}_1\)
= -0.85 eV - (-13.6 eV)
= 13.6 - 0.85 = 12.75 eV 
या \(\Delta \mathrm{E}=12.75 \times 1.6 \times 10^{-19} \mathrm{~J}\)
यदि इस फोटॉन की आवृत्ति v है तो

प्रश्न 7. 
(a) बोर मॉडल का उपयोग करके किसी हाइड्रोजन परमाणु में n = 1, 2 व 3 स्तरों पर इलेक्ट्रॉन की चाल परिकलित कीजिए।
(b) इनमें से प्रत्येक स्तर के लिए कक्षीय अवधि परिकलित कीजिए।
हल: 
(a) हाइड्रोजन परमाणु के स्तर की कक्षा की त्रिज्या
∆E₁₂ = E₂ - E₁
= -3.4 - (-13.6)
= 13.6 - 3.4 = 10.2 eV
∆E₁₃ = E₃ - E₄
= -1.51 - (-13.6)
= 13.6 - 1.51 = 12.09 eV
∆E₁₄ = E₄ - E₁
= -0.85 - (-13.6)
= 13.6 - 0.85 = 12.75 eV 
यहाँ e = 16 x 10^-19 C, h = 6.62 x 10^-34 Js,\( \frac{1}{4 \pi \varepsilon_0} -9\) x 10⁹ N - m²/C²
∴ \(\mathrm{V}_n=\frac{9 \times 10^9 \times 2 \times 3.14 \times\left(1.6 \times 10^{-19}\right)^2}{n \times 662 \times 10^{-34}}\)
या \(\mathrm{V}_n=\frac{21.86 \times 10^5}{n} \mathrm{~ms}^{-1}\)
∴ n = 1 के लिए,
V₁ = \(\frac{21.8 \times 10^5}{1}\) = 21.8 x 10⁵ ms^-1
या V₁ = 2.18 x 10⁶ ms^-1
n = 2 के लिए,
\(\mathrm{V}_2=\frac{2 \cdot 18 \times 10^6}{2}=1.09 \times 10^6 \mathrm{~ms}^{-1}\)
n = 3 के लिए,
\(V_3=\frac{2.18 \times 10^6}{3}=7.27 \times 10^5 \mathrm{~ms}^{-1}\)

(b) कक्षीय अवधि \(\mathrm{T}=\frac{2 \pi r}{\mathrm{~V}}\) 
चूँकि r₁ = 0.53 x 10^-10 m
\(\begin{aligned} T_1 &=\frac{2 \pi \times 0.53 \times 10^{-10} \mathrm{~m}}{2.19 \times 10^6} \\ &=1.52 \times 10^{-16} \mathrm{~s} \end{aligned}\)
एवं r₂ = 4r₁ तथा V₂ = \(\frac{1}{2} V_1\)
⇒ T₂ = 8T₁ तथा 8 x 1.52 x 10^-16 s
= 1.126 x 10^-15 s
r₃ = 9r₁ तथा V₃ = \(\frac{1}{3} V_1\)
∴ T₃ = 27 T₁ = 27 x 1.52 x 10^-16 s
= 4.1 x 10^-15 s

प्रश्न 8.
हाइड्रोजन परमाणु में अन्तरतम इलेक्ट्रॉन - कक्षा की त्रिज्या 5.3 x 10^-11 m है। 
कक्षा n = 2 और n = 3 की त्रिज्याएँ क्या हैं? 
उत्तर: 
हाइड्रोजन परमाणु में वीं कक्षा की त्रिज्या
\(r_n=\frac{\varepsilon_0 h^2}{\pi m e^2} n^2\)
∴ \(r_n \propto n^2\)
अत: \(\frac{r_2}{r_1}=\left(\frac{n_2}{n_1}\right)^2=\left(\frac{2}{1}\right)^2=4\)
∴ r₂ = 4r₁ = 4 x 5.3 x 10^-11 m
या r₂ = 2.12 x 10^-10 m
पुनः \(\frac{r_3}{r_1}=\left(\frac{3}{1}\right)^2=\frac{9}{1}=9\)
∴ r₃ = 9r₁ = 9 x 5.3 x 10^-11 m
या r₃ = 4.77 x 10^-10 m

प्रश्न 9. 
कमरे के ताप पर गैसीय हाइड्रोजन पर किसी 12.5 eV की इलेक्ट्रॉन पुंज की बमबारी की गई। किन तरंगदैयों की श्रेणी उत्सर्जित होगी?
उत्तर: 
हाइड्रोजन परमाणु के लिए
E_n = \(-\frac{13 \cdot 6}{n^2} eV\)

E₁ = \(-\frac{13 \cdot 6}{1^2}\) = -13.6 eV,
E₂ = \(-\frac{136}{4}\) = - 3.4 eV,
E₃ = \(-\frac{136}{9}\) = - 1.51 eV,
E₄ = \(-\frac{136}{16}\) = -0.85 eV
अतः n = 1 से n = 2, 3, 4 ऊर्जा स्तरों तक उत्तेजित होने के लिए आवश्यक ऊर्जाएँ
∆E₁₂ = E₂ - E₁
= -3.4 - (-13.6)
= 13.6 - 3.4 = 10.2 eV
∆E₁₃ = E₃ - E₁
= -1.51 - (-13.6)
= 13.6 - 1.51 = 12.09 eV
∆E₁₄ = E₄ - E₁
= -0.85 - (-13.6)
= 13.6 - 0.85 = 12.75 eV 
परन्तु प्रश्न के अनुसार इलेक्ट्रॉन पुंज की बमबारी की जाने वाली ऊर्जा
∆E = 12.5 eV
∵ \(\Delta \mathrm{E}_{14}>\Delta \mathrm{E}\)
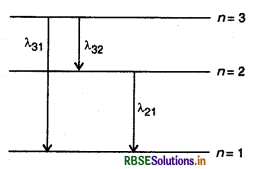
∴ हाइड्रोजन परमाणु उत्तेजित होकर n = 3 कक्षा में जायेगा। इस कक्षा (n = 3) से मूल अवस्था (n = 1) के लिए सम्भव संक्रमण उपर्युक्त चित्र में दिखाया गया है।

अतः उत्सर्जित तरंगदैर्ध्य निम्नलिखित होंगे-
लाइमन श्रेणी λ₃₁ = 1027 Å, λ₂₁ = 1216 Å
बामर श्रेणी λ₃₂ = 6567 Å

प्रश्न 10. 
बोहर मॉडल के अनुसार सूर्य के चारों ओर 1.5 x 10¹¹ m त्रिज्या की कक्षा में, 3 x 10⁴ ms^-1 के कक्षीय वेग से परिक्रमा करती पृथ्वी की अभिलाक्षणिक क्वाण्टम संख्या ज्ञात कीजिए। (पृथ्वी का द्रव्यमान = 6.0 x 10²⁴ kg)। 
हल: 
बोहर के द्वितीय अभिगृहीत के अनुसार,
\(m V r=n \times \frac{h}{2 \pi}\)
∴ \(n=\frac{2 \pi m v r}{h}\)
यहाँ m = 6.0 x 10²⁴ kg, v = 3 x 10⁴ ms^-1, r = 1.5 x 10¹¹ m
∴\( n=\frac{2 \times 3.14 \times 6 \times 10^{24} \times 3 \times 10^4 \times 1.5 \times 10^{11}}{6.63 \times 10^{-34}}\)
= 2.56 x 10⁷⁴

प्रश्न 11. 
निम्नलिखित प्रश्नों के उत्तर दीजिए जो आपको थॉमसन और रदरफोर्ड मॉडल में अन्तर समझने हेतु अच्छी तरह से सहायक हैं-
(a) क्या थॉमसन मॉडल में पतली स्वर्ण - पन्नी से प्रकीर्णित - कणों का पूर्वानुमानित (predicted) औसत विक्षेपण कोण, रदरफोर्ड मॉडल द्वारा पूर्वानुमानित मान में अत्यन्त कम, लगभग समान अथवा अत्यधिक बड़ा है?
(b) थॉमसन मॉडल द्वारा पूर्वानुमानित पश्च प्रकीर्णन (backward seattering) की प्रायिकता (अर्थात् α - कणों का 90° से बड़े कोणों पर प्रकीर्णन) रदरफोर्ड मॉडल द्वारा पूर्वानुमानित मान से अत्यन्त कम, लगभग समान अथवा अत्यधिक है?
(c) अन्य कारकों को नियत रखते हुए, प्रयोग द्वारा यह पाया गया है कि कम मोटाई t के लिए, मध्यम कोणों पर प्रकीर्णित α - कणों की रैखिक निर्भरता t के अनुक्रमानुपाती है। t पर यह रैखिक निर्भरता क्या संकेत करती है?
(d) किस मॉडल में α - कणों के पतली पन्नी से प्रकीर्णन के पश्चात् औसत प्रकीर्णन कोण के परिकलन हेतु बहु प्रकीर्णन की उपेक्षा करना पूर्णतः गलत है? 
उत्तर:
(a) औसत विक्षेपण कोण दोनों मॉडलों के लिए लगभग समान है।
(b) थॉमसन मॉडल द्वारा पूर्वानुमानित पश्च प्रकीर्णन की प्रायिकता, रदरफोर्ड मॉडल द्वारा पूर्वानुमानित मान की तुलना में अत्यन्त कम है।
(c) t पर रैखिक निर्भरता (linear dependence) यह प्रदर्शित करती है कि प्रकीर्णन मुख्यतः एकल संघट्ट (single collision) के कारण होता है। मोटाई t के बढ़ने के साथ लक्ष्य स्वर्ण नाभिकों की संख्या (target gold nucleus) रैखिक रूप से बढ़ती है, अत: α - कणों के स्वर्ण - नाभिक से एकल संघट्ट की सम्भावना रैखिक रूप से बढ़ती है।
(d) थॉमसन मॉडल में परमाणु का सम्पूर्ण धनावेश एवं द्रव्यमान परमाणु में समान रूप से वितरित (distributed) रहता है, अत: एकल संघट्ट α - कणों को अल्प कोणों (small angles) से विक्षेपित कर पाता है। अत: इस मॉडल में औसत प्रकीर्णन कोण का परिकलन, बहुप्रकीर्णन (multiple deflection) के आधार पर ही किया जा सकता है। दूसरी ओर रदरफोर्ड मॉडल में प्रकीर्णन एकल संघट्ट के कारण होता है, अतः बहुप्रकीर्णन की उपेक्षा की जा सकती है।

प्रश्न 12. 
हाइड्रोजन परमाणु में इलेक्ट्रॉन एवं प्रोटॉन के मध्य गुरुत्वाकर्षण, कूलॉम आकर्षण से लगभग 10^-40 के गुणक से कम है। इस तथ्य को देखने का एक वैकल्पिक उपाय यह है कि यदि इलेक्ट्रॉन एवं प्रोटॉन गुरुत्वाकर्षण द्वारा सम्बद्ध हों तो किसी हाइड्रोजन परमाणु में प्रथम बोर कक्षा की त्रिज्या का अनुमान लगाइए। आप मनोरंजक उत्तर पायेंगे।
उत्तर: 
यदि हाइड्रोजन परमाणु में इलेक्ट्रॉन एवं प्रोटॉन के मध्य गुरुत्वाकर्षण बन्धन मानें तो

प्रश्न 13. 
जब कोई हाइड्रोजन परमाणु स्तर n से स्तर (n - 1) पर व्युत्तेजित (de - excites) होता है तो उत्सर्जित विकिरण की आवृत्ति हेतु व्यंजक प्राप्त कीजिए। n के अधिक मान हेतु, दर्शाइए कि यह आवृत्ति, इलेक्ट्रॉन की कक्षा में परिक्रमण की क्लासिकी आवृत्ति के बराबर है। 
हल: 
बोहर की परिकल्पना से,
\(m \mathrm{~V} r=n \times \frac{h}{2 \pi}\) .................(1)
यदि परिक्रमण - आवृत्ति vC हो तो
∵ V = rω
∴ V = r.2πvC

बोहर के तृतीय अभिगृहीत के अनुसार स्तर n से स्तर (n - 1) को उत्सर्जन संक्रमण के दौरान उत्सर्जित फोटॉन के लिए
n के बड़े मानों के लिए, 
2n - 1 = 27  एवं n - 1 = 1
∴ \(v_{\mathrm{B}}=\frac{c \cdot 2 n}{n^2 \cdot n^2} \times \frac{m e^4}{8 \varepsilon_0^2 c h^3}\)
या \(v_{\mathrm{B}}=\frac{m e^4}{4 \varepsilon_0^2 h^3 n^3}\) ..................(3)
समी (2) व (3) की तुलना करने पर के बड़े मानों के लिए,
v_B = v_C ................(4)
समी. (4) से स्पष्ट है कि n के बड़े मानों के लिए वीं कक्षा में इलेक्ट्रॉन की क्लासिकी घूर्णन आवृत्ति (frequency of revolution), हाइड्रोजन परमाणु द्वारा ऊर्जा स्तर से (n = 1) वें ऊर्जा स्तर में जाने के दौरान उत्सर्जित विकिरण की आवृत्ति के बराबर होती है।

प्रश्न 14. 
क्लासिकी रूप में किसी परमाणु में इलेक्ट्रॉन नाभिक के चारों ओर किसी भी कक्षा में हो सकता है। तब (typical) प्रारूपी परमाण्वीय साइज किससे निर्धारित होता है? परमाणु अपने प्रारूपी साइज की अपेक्षा दस हजार गुना बड़ा क्यों नहीं है? इस प्रश्न ने बोहर को अपने प्रसिद्ध परमाणु मॉडल, जो आपने पाठ्य - पुस्तक में पढ़ा है, तक पहुंचने से पहले बहुत अलझन (puzzled) में डाला था। अपनी खोज से पूर्व उन्होंने क्या किया होगा, इसका अनुकरण करने के लिए हम मूल नियतांकों की प्रकृति के साथ निम्न गतिविधि करके देखें कि क्या हमें लम्बाई की विमा वाली कोई राशि प्राप्त होती है, जिसका साइज लगभग परमाणु के ज्ञात साइज (~10^-10 m) के बराबर है।
(a) मूल नियतांकों e, m_e और c से लम्बाई की विमा वाली राशि की रचना कीजिए। उसका संख्यात्मक मान भी निर्धारित कीजिए।
(b) आप पायेंगे कि (a) प्राप्त लम्बाई परमाण्वीय विमाओं (atomic dimensions) के परिमाण की कोटि से काफी छोटी है। इसके अतिरिक्त इसमें c सम्मिलित है। परन्तु परमाणुओं की ऊर्जा अधिकतर अनापेक्षिकीय क्षेत्र (non - relativistic domain) में है जहाँ c की कोई अपेक्षित भूमिका नहीं है। इसी तर्क ने बोहर को का परित्याग (discard) कर सही परमाण्वीय साइज को प्राप्त करने के लिए 'कुछ अन्य' देखने के लिए प्रेरित किया। इस समय प्लांक नियतांक h का कहीं और (elsewhere) पहले ही आविर्भाव (appearance) हो चुका था। बोहर की सूक्ष्म दृष्टि ने पहचाना कि h, m_e और e के प्रयोग से ही सही परमाणु साइज प्राप्त होगा। अत: h, m_e और e लम्बाई की विमा वाली किसी राशि की रचना कीजिए और पुष्टि कीजिए कि इसका संख्यात्मक मान वास्तव में सही परिणाम की कोटि का है। 
हल: 
(a) प्रश्न में दी राशियों के विमीय सूत्र
e का विमीय सूत्र = [A¹T¹] 
m_e  का विमीय सूत्र = [M¹]
c का विमीय सूत्र = [L^-1T^-1]
तथा \(\frac{1}{4 \pi \varepsilon_0}\) का विमीय सूत्र = [M¹L³T^-4A^-2]

माना लम्बाई की विमा वाली राशि L दी गई राशियों पर निम्न समीकरण के अनुसार निर्भर करती है-
\(\mathrm{L} \propto e^x m_e^y c^z\left(\frac{1}{4 \pi \varepsilon_0}\right)^u\)
या \(\mathrm{L}=\mathrm{K} e^x m_e^y c^z\left(\frac{1}{4 \pi \varepsilon_0}\right)^u\) ......................(1)
जहाँ K एक नियतांक है।
L.H.S. का वि. सूत्र = [M⁰L¹T⁰A⁰] 
R.H.S. का वि. सूत्र = [A¹T¹]^x [M¹]^y [L¹T^-1]^z [M¹L³T^-4 A^-2]^u
= A^xT^xM^x L^zT^-z M^u L^3u T^-4u A^-2u
= [M^{(y + u)} L^{(z + 3u)} T^{(x - z - 4u)} A^{(x - 2u)}]
सूत्र (1) की सत्यता के लिए दोनों पक्षों को विमाएँ समान होनी चाहिए। अतः विमाओं की तुलना करने पर,
y + u = 0 .................(2)
z + 3u = 1 ................(3)
x - z - 4u = 0 ..................(4)
x - 2u = 0 ..................(5)
समी. (3) व (4) को जोड़ने पर,
x- u = 1 ...............(6)
समी. (6) में से (5) को घटाने पर,
u = 1
u का मान समी. (6) में रखने पर,
x - 1 = 1 ⇒ x = 2
समी. (2) में u का मान रखने पर,
y + 1 = 0 ⇒ y = -1
समी. (3) में u का मान रखने पर,
z + 3 = 1 ⇒ z = -2  
समी. (1) में K का मान 1 लेकर अन्य मान रखने पर,
\(\mathrm{L}=e^2 \cdot m_e^{-1} c^{-2}\left[\frac{1}{4 \pi \varepsilon_0}\right]^1\)
या \(\mathrm{L}=\frac{1}{4 \pi \varepsilon_0} \cdot \frac{e^2}{m_e \cdot c^2}\)
सभी प्रतीकों के मान रखने पर,
\(L=\frac{\left(9 \times 10^9\right) \times\left(1.6 \times 10^{-19}\right)^2}{\left(9 \cdot 1 \times 10^{-31}\right) \times\left(3 \times 10^8\right)^2} \mathrm{~m}\)
या L = 2.81 x 10^-15 m
परन्तु परमाणु का ज्ञात साइज (~10^-10 m) है। अतः स्पष्ट है कि यह दूरी परमाणु के ज्ञात साइज की तुलना में लगभग 10⁵ गुनी छोटी है।

(b) अब c के स्थान पर h लेने पर \(\left(\hbar=\frac{h}{2 \pi}\right)\),
h का विमीय सूत्र = [M¹L²T^-1] 
अत: (a) की भाँति माना अभीष्ट राशि
\(\mathrm{L}=e^x m_e^y \hbar^z\left[\frac{1}{4 \pi \varepsilon_0}\right]^u\) .....................(1)
या [M⁰L¹T⁰A⁰] = [A¹T¹]^x [M¹L²T^-1]^z [M¹L³T^-4A^-2]^u
या \(\begin{aligned} &{\left[\mathrm{M}^0 \mathrm{~L}^1 \mathrm{~T}^0 \mathrm{~A}^0\right]=\left[\mathrm{M}^{(y+z+u)} \mathrm{L}^{(2 z+3 u)}\right.} \\ &\left.\mathrm{T}^{(x-z-4 u)} \mathrm{A}^{(x-2 u)}\right] \end{aligned}\)
विमाओं की तुलना करने पर,
y + z + u = 0 .......................(2)
2z + 3u = 1 ..........................(3)
x - z - 4u = 0 .......................(4)
x - 2u = 0 .........................(5)
इन समीकरणों को हल करने पर,
u = -1, z = 2, y = -1, x = -2
अतः समी. (1) से,

यही परमाणु के आमाप (size) की कोटि है।

प्रश्न 15. 
हाइड्रोजन परमाणु की प्रथम उत्तेजित अवस्था में इलेक्ट्रॉन की कुल ऊर्जा लगभग - 3.4 eV है।
(a) इस अवस्था में इलेक्ट्रॉन की गतिज ऊर्जा क्या है? 
(b) इस अवस्था में इलेक्ट्रॉन की स्थितिज ऊर्जा क्या है?
(c) यदि स्थितिज ऊर्जा के शून्य स्तर के चयन में परिवर्तन कर दिया जाये तो ऊपर दिये गये उत्तरों में से कौन - सा उत्तर परिवर्तित होगा?
उत्तर: 
(a) माना प्रथम उतेजित अवस्था में कक्षा की त्रिज्या r है। अत: नाभिक एवं इलेक्ट्रॉन के मध्य सन्तुलन को अवस्था में

(b) समी. (3) से इलेक्ट्रॉन की स्थितिज ऊर्जा
U = -2K = -2 x 3.4 eV
या U = -6.8 eV

(c) यदि स्थितिज ऊर्जा के शून्य को बदल दिया जाये तो इलेक्ट्रॉन की स्थितिज ऊर्जा तथा कुल ऊर्जा बदल जायेगी लेकिन गतिज ऊर्जा अपरिवर्तित रहेगी।

प्रश्न 16. 
यदि बोहर का क्वाण्टमीकरण अभिगृहीत (कोणीय संवेग =\( n \times \frac{h}{2 \pi}\)) प्रकृति का मूल नियम है तो यह ग्रहीय गति की दशा में भी लागू होना चाहिए। तब हम सूर्य के चारों ओर ग्रहों की कक्षाओं के क्वाण्टमीकरण के विषय में कभी चर्चा क्यों नहीं करते?
हल: 
यदि बोहर के क्वाण्टम सिद्धान्त को पृथ्वी के लिए लागू करें तो
\(m v r=n \frac{h}{2 \pi}\)
या \(n=\frac{2 \pi m v r}{h}\)
या \(n=\frac{2 \times 3.14 \times\left(6 \times 10^{24}\right) \times\left(3 \times 10^4\right) \times\left(1.49 \times 10^{11}\right)}{6.62 \times 10^{-34}}\)
\(=2.49 \times 10^{74}\)
या \(n \approx 10^{74}\)
क्वाण्टम संख्या n का यह मान बहुत अधिक है अत: इसका अर्थ यह हुआ कि ग्रहों की गति से सम्बद्ध कोणीय संवेग तथा ऊर्जा \(\frac{h}{2 \pi}\) की तुलना में अत्यन्त बड़ी है। n के इतने उच्च मान के लिए किसी ग्रह के बोहर मॉडल के दो क्रमागत क्वाण्टमीकृत (continuous quantised) ऊर्जा स्तरों के बीच ग्रह के कोणीय संवेग तथा ऊर्जाओं के अन्तर किसी ऊर्जा स्तर में ग्रह के कोणीय संवेग तथा ऊर्जा की तुलना में नगण्य हैं, इसी कारण ग्रहों की गति में ऊर्जा स्तर क्वाण्टमीकृत होने के स्थान पर सतत प्रतीत होते हैं।

प्रश्न 17. 
प्रथम बोहर - त्रिज्या और म्यूओनिक हाइड्रोजन परमाणु [ अर्थात् कोई परमाणु जिसमें लगभग 207 m_e द्रव्यमान ऋणावेशित म्यूऑन (µ^-) प्रोटॉन के चारों ओर घूमता है ] की निम्नतम अवस्था की त्रिज्या एवं ऊर्जा को प्राप्त करने का परिकलन कीजिए।
हल: 
माना म्यूऑन का द्रव्यमान m_µ = 207 m_e है। अत: बोहर के सिद्धान्त से,
F_c = F_e
या \(\frac{m_\mu \mathrm{V}^2}{r}=\frac{1}{4 \pi \varepsilon_0} \frac{e^2}{r^2}\) .................(1)
तथा \(m_\mu \mathrm{V} r=n \frac{n}{2 \pi}\) ....................(2)
समी. (1) व (2) से v को विलुप्त करने पर,
\(r=\frac{\varepsilon_0 h^2 n^2}{\pi m_\mu e^2}\)
\(m_\mu=207 m_e\) रखने पर,
\(r=\frac{\varepsilon_0 h^2 n^2}{207 \pi m_e e^2}\)
म्यूऑन को निम्नतम ऊर्जा अवस्था के लिए, n = 1
∴ \(r_\mu=\frac{\varepsilon_0 h^2}{207 \pi m_e e^2}\)
परन्तु \(\frac{\varepsilon_0 h^2}{\pi m_e e^4}\) = सामान्य हाइड्रोजन परमाणु की निम्नतम की त्रिज्या = 0.53 x 10^-10 m
∴ \(r_\mu=\frac{0.53 \times 10^{-10}}{207}\)
= 2.56 x 10^-13 m
इसी प्रकार ऊर्जा
\(\mathrm{E}_n=-\frac{m e^4}{8 \varepsilon_0^2 h^2} \cdot \frac{1}{n^2}\)
या \(\mathrm{E}_n \propto m\) (निम्नतम अवस्था के लिए n = 1) 
∴ \(\frac{\mathrm{E}_\mu}{\mathrm{E}_e}=\frac{m_\mu}{m_e}=\frac{207 m_e}{m_e}=207\)
∴ E_µ = 207E_e
= 207(-13.6 eV)
= -2.8 x 10³ eV = -2.8 keV