RBSE Solutions for Class 12 Physics Chapter 11 विकिरण तथा द्रव्य की द्वैत प्रकृति

Rajasthan Board RBSE Solutions for Class 12 Physics Chapter 11 विकिरण तथा द्रव्य की द्वैत प्रकृति Textbook Exercise Questions and Answers.

RBSE Class 12 Physics Solutions Chapter 11 विकिरण तथा द्रव्य की द्वैत प्रकृति

RBSE Class 12 Physics विकिरण तथा द्रव्य की द्वैत प्रकृति Textbook Questions and Answers

प्रश्न 1. 
30 kV के इलेक्ट्रॉनों के द्वारा उत्पन्न X - किरणों की (a) उच्चतम आवृत्ति, (b) निम्नतम तरंगदैर्घ्यं प्राप्त कीजिए। 
हल: 
दिया है: इलेक्ट्रॉनों का त्वरक विभव
V = 30 kV = 30 x 10³ V 
∴ लक्ष्य से टकराने वाले इलेक्ट्रॉनों की कर्जा
E = V.e जूल 
हम जानते हैं कि लक्ष्य से टकराने पर इलेक्ट्रॉन की सम्पूर्ण ऊर्जा जब X - किरण फोटॉन में बदल जाती है तो उच्चतम आवृति एवं निम्नतम तरंगदैर्ध्य की X - किरणें प्राप्त होती हैं।
(a) ∴ E = hvmax
∴ \(v_{\max }=\frac{\mathrm{E}}{h}=\frac{30 \times 10^3 \times 1.6 \times 10^{-19}}{6.62 \times 10^{-34}} \mathrm{~Hz} = \frac{4.8}{6.62} \times 10^{19}=0.725 \times 10^{19}\)
= 7.25 x 10¹⁸ Hz

(b) ∵ X - किरणे प्रकाश के वेग से चलती है अत:
c = vλ  = vmax.λmax
∴ \(\lambda_{\min }=\frac{c}{v_{\max }}=\frac{3 \times 10^8}{7.25 \times 10^{18}}\)
= \(\frac{3}{7 \cdot 25} \times 10^{-10}\)
= 0.41379 x 10^-10 m
= 0.414 Å

प्रश्न 2. 
सीजियम धातु का कार्य - फलन 2.14 eV है। जब 6 x 10¹⁴ Hz आवृत्ति का प्रकाश थातु पृष्ठ पर आपतित होता है, तो प्रकाश इलेक्ट्रॉनों का उत्सर्जन होता है।
(a) उत्सर्जित इलेक्ट्रॉनों की उच्चतम गतिज ऊजाँ, 
(b) निरोधी विभव (stopping potential) और 
(c) उत्सर्जित प्रकाशिक इलेक्ट्रॉनों की उच्चतम चाल कितनी है? 
हल: 
दिया है: कार्य - फलन
\(\phi_0\) = 2.14 eV = 2.14 x 1.6 x 10^-19 J
आपतित प्रकाश की आवृत्ति
v = 6 x 10¹⁴ Hz, (K)max = ?, V₀ = ?, v_max = ? 

(a) फोटॉन की ऊर्जा

∵आइन्स्टीन के अनुसार,
\(\mathrm{E}=\phi_0+\mathrm{K}_{\max }\)
∴ \((\mathrm{K})_{\max }=\mathrm{E}-\phi_0=(2 \cdot 475-2 \cdot 14) \mathrm{eV}\)
= 0.335 eV
या (K)_max = 0.34 eV

(b) ∵ (K)_max = V₀.e जूल
∴ 0.34 x e = V₀ x e
या V₀ = 0.34 वोल्ट

(c) ∵ \(\frac{1}{2} m v_{\max }^2=\mathrm{V}_0 e\)
∴ \(v_{\max }=\sqrt{\frac{2 \mathrm{~V}_0 \cdot e}{m}}\)
\(\begin{aligned} &=\sqrt{\frac{2 \times 0.34 \times 1.6 \times 10^{-19}}{9.1 \times 10^{-31}}} \\ &=3.44 \times 10^5 \mathrm{~ms}^{-1} \end{aligned}\)

प्रश्न 3. 
एक विशिष्ट प्रयोग (In a certain experiment) में प्रकाश - विद्युत् प्रभाव की अंतक वोल्टता (cut - off potential) 1.5 V है। असर्जित प्रकाशिक इलेक्ट्रॉनों की उच्चतम गतिज ऊर्जा कितनी है?
हल: 
अंतक वोल्टता V₀ = 1.5 V
∴ इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा 
(K)_max = \(\frac{1}{2} m v_{\max }^2\) = eV₀ जूल
= 1.5 x 1.6 x 10^-19 J
= 2.40 x 10^-19 J
\(=\frac{2 \cdot 4 \times 10^{-19}}{1.6 \times 10^{-19}} \mathrm{eV}\)
= 1.5 eV

प्रश्न 4. 
632.8 nm तरंगदैर्ध्य का एकवर्णीय प्रकाश (monochromatic light) एक हीलियम - निऑन लेसर के द्वारा उत्पन्न किया जाता है। उत्सर्जित शक्ति 9.42 mW है।
(a) प्रकाश के किरण - पुंज में प्रत्येक फोटॉन की ऊजां तथा संवेग प्राप्त कीजिए।
(b) इस किरण - पुंज के द्वारा विकिरित (radiated) किसी लक्ष्य (target) पर औसतन कितने फोटॉन पहुँचेंगे? (यह मान लीजिए कि किरण - पुंज की अनुप्रस्थ काट एकसमान है जो लक्ष्य के क्षेत्रफल से कम है, तथा
(c) एक हाइड्रोजन परमाणु को फोटॉन के बराबर संवेग प्राप्त करने के लिए कितनी तेज चाल से चलना होगा?
हल: 
दिया है: 
उत्सर्जित शक्ति P = 9.42 mW = 9.42 x 10^-3 W
λ = 632.8 nm = 632.8 x 10^-9 m 

(a) प्रत्येक फोटॉन की ऊर्जा
E = \(\frac{h c}{\lambda}=\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{632.8 \times 10^{-9}}\) J
= 0.03138 x 10^-17 J
= 3.14 x 10^-19 J
संवेग \(p=\frac{h}{\lambda}=\frac{6 \cdot 62 \times 10^{-34}}{632 \cdot 8 \times 10^{-9}}\)
= 3 x 10¹⁶
1.05 x 10^-27 kg ms^-1

(b) माना प्रति सेकण्ड लक्ष्य पर पहुँचने वाले फोटॉनों की संख्या = n
∴ n x एक फोटॉन की ऊर्जा - उत्सर्जित शक्ति
या n x E = P
∴ \(n=\frac{\mathrm{P}}{\mathrm{E}}=\frac{9 \cdot 42 \times 10^{-3}}{3 \cdot 14 \times 10^{-19}}=3 \times 10^{16}\)
अतः प्रति सेकण्ड निकलने वाले फोटॉन को संख्या
= 3 x 10¹⁶

(c) हाइड्रोजन परमाणु का द्रव्यमान
m = 1.67 x 10^-27 kg
यदि हाइड्रोजन परमाणु का वेग = v 
तो संवेग p = mv
∵ p = mv = फोटॉन का संवेग 
∴ \(v=\frac{p}{m}=\frac{1.05 \times 10^{-27}}{1.67 \times 10^{-27}}\)
= 0.6287 ms^-1
या v = 0.63 ms^-1 

प्रश्न 5. 
पृथ्वी के पृष्ठ पर पहुंचने वाले सूर्य - प्रकाश का ऊर्जा - अभिवाह (Flux) 1.388 x 10³ Wm^-2 है। लगभग कितने फोटॉन प्रति वर्ग मीटर प्रति सेकण्ड पृथ्वी पर आपतित होते हैं? यह मान लीजिए कि सूर्य - प्रकाश में फोटॉन का औसत तरंगदैर्ध्य 550 nm है।
हल: 
दिया है: λ = 550 nm = 550 x 10^-9 m 
पृथ्वी पर सूर्य के प्रकाश का आपतित फ्लक्स
\(\phi\) = 1.388 x 10³ Wm^-2 
एक फोटॉन की ऊर्जा
\(\mathrm{E}=\frac{h c}{\lambda}=\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{550 \times 10^{-9}}\)
या E = 3.6 x 10^-19 J
यदि पृथ्वी पर प्रति सेकण्ड प्रति वर्ग मीटर आपतित फोटॉनों की संख्या = n
तो \(\phi\) = nE
∴ \(n=\frac{\phi}{\mathrm{E}}=\frac{1.388 \times 10^3}{3.6 \times 10^{-19}}\)
= 3.85 x 10²¹
या n ≈ 4 x 10²¹

प्रश्न 6. 
प्रकाश - वैद्युत प्रभाव के एक प्रयोग में, प्रकाश आवृत्ति एवं अंतक वोल्टता के मध्य ग्राफ की ढलान 4.12 x 10^-15 Vs प्राप्त होती है। प्लांक नियतांक का मान ज्ञात कीजिए। 
हल: 
दिया है: वक्र की ढलान
m = tanθ = 4.12 x 10^-15 Vs 
आइन्स्टीन के प्रकाश - वैद्युत् समीकरण से-
(K)_max = V0.e = h (v - v₀)
या \(\mathrm{V}_0=\frac{h}{e}, \boldsymbol{v}-\frac{h v_0}{e}\) .............................(1)

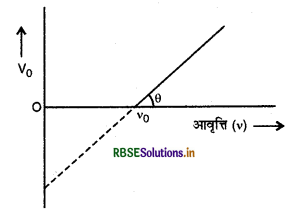
इस समीकरण की तुलना सरल रेखा के समीकरण y= mx + c से करने पर,
\(m=\frac{h}{e}\)
∴ h = m x e
= 4.12 x 10^-15 x 1.6 x 10^-19
= 6.592 x 10^-34
= 6.59 x 10^-34 Js

प्रश्न 7. 
एक 100W सोडियम लैम्प सभी दिशाओं में एकसमान ऊर्जा विकिरत करता है। लैम्प को एक ऐसे बड़े गोले (large sphere) के केन्द्र पर रखा गया है जो इस पर आपतित सोडियम के सम्पूर्ण प्रकाश को अवशोषित करता है। सोडियम प्रकाश की तरंगदैर्ध्य 589 nm है।
(a) सोडियम प्रकाश से जुड़े प्रति फोटॉन की ऊर्जा कितनी है? 
(b) गोले को किस दर से फोटॉन प्रदान (delivered) किये जा रहे हैं? 
हल: 
दिया है: P= 100 W, λ = 589 nm
= 589 x 10^-9 m 
(a) प्रत्येक फोटॉन की ऊर्जा,
\(\mathrm{E}=\frac{h c}{\lambda}=\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{589 \times 10^{-9}} \mathrm{~J}\)
= 0.0337 x 10^-17 J
= 3.37 x 10^-19 J
या \(E=\frac{3.37 \times 10^{-19}}{1.6 \times 10^{-19}}\)
= 2.10625 eV
= 2.1 eV

(b) माना लैम्प द्वारा गोले को प्रति सेकण्ड n फोटॉन प्रदान किये जाते है।
अत: n x एक फोटॉन की ऊर्जा = बल्ब की विकिरण शक्ति 
या n x E = P
∴ \(n=\frac{\mathrm{P}}{\mathrm{E}}=\frac{100}{3.37 \times 10^{-19}}\)
= 29.67 x 10¹⁹
= 2.97 x 10²⁰
≈ 3 x 10²⁰

प्रश्न 8. 
किसी धातु की देहली आवृत्ति 3.3 x 10¹⁴ Hz है। यदि 8.2 x 10¹⁴ Hz आवृत्ति का प्रकाश धातु पर आपतित हो तो प्रकाश - वैद्युत उत्सर्जन के लिए अन्तक वोल्टता (cut - off voltage) ज्ञात कीजिए।
हल: 
दिया है: v₀ = 3.3 x 10¹⁴ Hz, v = 8.2 x 10¹⁴ Hz, V₀ = ?

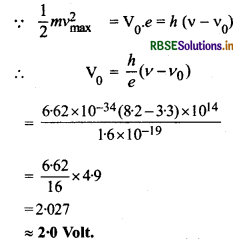
प्रश्न 9. 
किसी धातु के लिए कार्य- फलन 4.2 eV है। क्या यह धातु 330 nm तरंग के आपतित विकिरण के लिए प्रकाश - वैद्यत उत्सर्जन करेगी?
हल:
λ = 330 nm = 330 x 10^-9 m,\( \phi_0\)= 4.2 eV 
∴फोटॉन की ऊर्जा
\(\begin{aligned} \mathrm{E} &=\frac{h c}{\lambda e} \mathrm{eV} \\ &=\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{330 \times 10^{-9} \times 1.6 \times 10^{-19}} \\ &=3.76 \mathrm{eV} \end{aligned}\)
∵ \(\mathrm{E}<\phi_0\)
अतः धातु पृष्ठ से इलेक्ट्रॉन उत्सर्जित नहीं होंगे।

प्रश्न 10.
7.21 x 10¹⁴ Hz आवृत्ति का प्रकाश एक धातु पृष्ठ पर आपतित है। इस पृष्ठ से 6.0 x 10⁵ ms^-1 की उच्चतम गति से इलेक्ट्रॉन असर्जित हो रहे हैं। इलेक्ट्रॉनों के प्रकाश उत्सर्जन के लिए देहली आवृत्ति क्या है?
हल: 
v = 7.21 x 10¹⁴ Hz, vmax = 6.0 x 10⁵ ms^-1, v₀ = ?

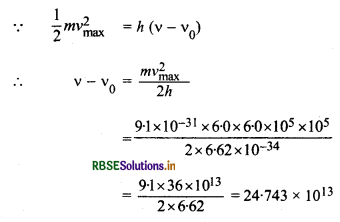
या v - v₀ = 2.47 x 10¹⁴ Hz
v₀ = v - 2.47 x 10¹⁴ Hz
= 7.21 x 10¹⁴ - 2.47 x 10¹⁴
= (7.21 - 2.47) x 10¹⁴
या v₀ = 4.74 x 10¹⁴ Hz

 
प्रश्न 11. 
488 nm तरंगदैर्ध्य का प्रकाश एक ऑर्गन लेसर से उपन्न किया जाता है, जिसे प्रकाश - विद्युत् प्रभाव के उपयोग में लाया जाता है। जब इस स्पेक्ट्रमी रेखा के प्रकाश को उत्सर्जक पर आपतित किया जाता है, तब प्रकाशिक इलेक्ट्रॉनों का निरोधी विभव (अन्तक विभव) 0.38 V है। उत्सर्जक के पदार्थ का कार्य - फलन ज्ञात कीजिए।
हल: 
दिया है: λ = 488 nm = 488 x 10^-9 m, V₀ =  0.38 V, \phi_0=?
फोटॉन को ऊर्जा
E = \(\frac{h c}{\lambda e} \mathrm{eV}\)
= \(\frac{6.6 \times 10^{-34} \times 3 \times 10^8}{488 \times 10^{-9} \times 1.6 \times 10^{-19}} \mathrm{eV}\)
= 2.54 eV
(K)_max = \(\frac{1}{2} m v_{\max }^2\)
= V₀.e J = V₀ eV
= 0.38 eV
∵ E = (K)_max + \(\phi_0\)
∴ \(\phi_0\) = E - (K)_max
= (2.54 - 0.38) eV
= 2.16 eV

प्रश्न 12.
56 V विभवान्तर के द्वारा त्वरित इलेक्ट्रॉनों का (a) संवेग और (b) डी - ब्रॉग्ली तरंगदैर्ध्य का परिकलन कीजिए।
हल: 
दिया है: त्वरक विभव V = 56 वोल्ट 
इलेक्ट्रॉन का द्रव्यमान m = 9.1 x 10^-31 kg,
e = 1.6 x 10^-19 C
(a) त्वरित इलेक्ट्रॉन की ऊर्जा
\(\frac{1}{2} m v^2=\mathrm{Ve}\)
∴ \(v=\sqrt{\frac{2 \mathrm{~V} . e}{m}}\)
\(=\sqrt{\frac{2 \times 56 \times 1.6 \times 10^{-19}}{9 \cdot 1 \times 10^{-31}}}\)
= 4.44 x 10⁶ ms^-1
∴इलेक्ट्रॉनों का संवेग
p = mv = 9.1 x 10^-31 x 4.44 x 10⁶
= 40.404 x 10^-25
= 4.04 x 10^-24 kg ms^-1

(b) इलेक्ट्रॉन से सम्बद्ध द्रव्य तरंगों को डी - ब्रॉग्ली तरंगदैध्य
λ = \(\frac{12.27}{\sqrt{V}}\) Å = \(\frac{12 \cdot 27}{\sqrt{56}}\) Å = 1.64 Å

प्रश्न 13. 
एक इलेक्ट्रॉन जिसकी गतिज ऊर्जा 120 eV है, उसका (a) संवेग, (b) चाल और (c) डी - ब्रॉग्ली तरंगदैर्ध्य क्या है?
हल: 
दिया है: K= 120 eV = 120 x 1.6 x 10^-19 
(a) इलेक्ट्रॉन की गतिज ऊर्जा
\(\mathrm{K}=\frac{1}{2} m y^2=\frac{m^2 v^2}{2 m}=\frac{p^2}{2 m}\)
∴ \(p=\sqrt{2 m \cdot \mathrm{K}}\)
\(=\sqrt{2 \times 9.1 \times 10^{-31} \times 120 \times 1 \cdot 6 \times 10^{-19}}\)
= 5.91 x 10^-24 kg ms^-1

(b) ∵ mv = p
∴ \(v=\frac{p}{m}=\frac{5.91 \times 10^{-24}}{9.1 \times 10^{-31}}\)
= 6.5 x 10⁶ ms^-1

(c) इलेक्ट्रॉन से सम्बद्ध दव्य तरंगों को डी - बॉग्ली तरंगदैर्ध्य
\(\lambda=\frac{h}{p}=\frac{6.62 \times 10^{-34}}{5.91 \times 10^{-24}}\)
= 0.112 nm

प्रश्न 14. 
सोडियम के स्पेक्ट्रमी उत्सर्जन रेखा के प्रकाश की तरंगदैर्ध्य 589 nm है। वह गतिज ऊर्जा ज्ञात कीजिए जिस पर (a) एक इलेक्ट्रॉन और (b) एक न्यूट्रॉन का डी - झॉग्ली तरंगदैर्ध्वं समान होगी। 
हल: 
λ = 589 nm = 589 x 10^-9 m
me = 9.1 x 10^-31 kg, mn = 1.67 x 10^-27 kg 
(a) इलेक्ट्रॉन की गतिज ऊर्जा

(b) इसी प्रकार न्यूट्रॉन की गतिज ऊर्जा

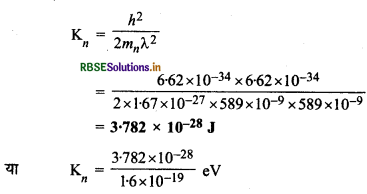
= 2.36 x 10^-9 eV

प्रश्न 15.
(a) एक 0.040 द्रव्यमान का बुलेट जो 1.0 km/s की चाल से चल रहा है, 
(b) एक 0.060 kg द्रव्यमान की गेंद जो 10ms^-1 की चाल से चल रही है, और 
(c) एक धूल कण जिसका द्रव्यमान 1.0 x 10^-9 kg और जो 2.2 ms^-1 की चाल से अनुगमित (drifting) हो रहा है, का डी - ब्रॉग्ली तरंगदैर्ध्य कितना होगा?
हल: 
(a) दिया है m = 0.04 kg
v = 1.0 km.s^-1 = 1.0 x 10³ ms^-1 
∴ डी - ब्रॉग्ली तरंगदैर्ध्य
\(\lambda=\frac{h}{m v}=\frac{6.62 \times 10^{-34}}{0.04 \times 1.0 \times 10^3}\)
= 1.655 x 10^-35 m

(b) यहाँ m = 0.06 kg, v = 1.0 ms^-1
∴\( \lambda=\frac{h}{m v}=\frac{6 \cdot 62 \times 10^{-34}}{0.06 \times 1.0}\)
= 1.1 x 10^-32 m
(c) यहाँ m = 1.0 x 10^-9 kg, v = 2.2 ms^-1
∴ \( \lambda=\frac{h}{m v}=\frac{6.62 \times 10^{-34}}{1.0 \times 10^{-9} \times 2.2}\)
= 3.01 x 10^-25 m

प्रश्न 16. 
एक इलेक्ट्रॉन और एक फोटॉन का तरंगदैर्ध्य 1.00 nm है। (a) इनका संवेग, (b) फोटोंन की ऊर्जा और (c) इलेक्ट्रॉन की गतिज ऊर्जा ज्ञात कीजिए। 
हल: 
यहाँ λ = 1.00 nm = 1.0 x 10^-9 m,
h = 6.62 x 10^-34 Js 
इलेक्ट्रॉन का द्रव्यमान me = 9.1 x 10^-31 kg
(a) ∵ डी - ब्रॉग्ली तरंगदैर्घ्य
\(\lambda=\frac{h}{p} \therefore p=\frac{h}{\lambda}\)
या \(p=\frac{6.62 \times 10^{-34}}{1.0 \times 10^{-9}}\)
= 6.62 x 10^-25 kg ms^-1

(b) फोटॉन की ऊर्जा यदि p है तो
E = \(\frac{h c}{\lambda}\) = p.c
= 6.62 x 10^-25 x 3 x 10⁸
= 1.986 x 10^-16 J
या E = \(\frac{1.986 \times 10^{-16}}{1.6 \times 10^{-19}}\) eV
= 1.24 x 10³ eV
(c) इलेक्ट्रॉन की ऊर्जा
K_e = \(\frac{1}{2} m_e v_e^2=\frac{p^2}{2 m_e}\)
= \(\frac{6.62 \times 10^{-25} \times 6.62 \times 10^{-25}}{2 \times 9.1 \times 10^{-31}}\)
= 2.41 x 10^-19 J
या K_e = \(\frac{2.41 \times 10^{-19}}{1.6 \times 10^{-19}}\) eV
= 1.51 eV
 

प्रश्न 17.
(a) न्यूट्रॉन की किस गतिज ऊर्जा के लिए डी - ब्रॉग्ली तरंगदैर्ध्य 1.40 x 10^-10 m होगा? 
(b) एक न्यूट्रॉन, जो पदार्थ के साथ तापीय साम्य (thermal equilibrium) में है और जिसकी 300 K पर औसत गतिज ऊर्जा \(\frac{3}{2} k T\) है, की भी डी - ब्रॉग्ली तरंगदैर्ध्य ज्ञात कीजिए।
हल: 
(a) दिया है: न्यूट्रॉन की डी - ब्रॉग्ली तरंगदैर्ध्य λ = 1.40 x 10^-10 m 
द्रव्यमान m = 1.67 x 10^-27 kg, E = ?

(b) दिया है: T = 300 K, k = 1.38 x 10^-23 JK^-1 (बोल्ट्स मैन नियतांक) 
∴ न्यूट्रॉन की गतिज ऊर्जा 
\(\mathrm{K}=\frac{3}{2} k \mathrm{~T}=\frac{3}{2} \times 1.38 \times 10^{-23} \times 300\)
= 6.21 x 10^-21 J
∵ K गतिज ऊर्जा वाले गतिशील कण की डी - ब्रॉग्ली तरंगदैर्ध्य
\(\begin{aligned} \lambda &=\frac{h}{\sqrt{2 m K}} \\ &=\frac{6.62 \times 10^{-34}}{\sqrt{2 \times 1.67 \times 10^{-27} \times 6.21 \times 10^{-21}}} \\ &=0.145 \mathrm{~nm} \end{aligned} \)

प्रश्न 18.
यह दशाईए कि विद्युत् - चुम्बकीय विकिरण की डी - ब्रॉग्ली तरंगदैर्ध्य इसके फोटॉन की तरंगदैर्ध्य के बराबर है।
हल: 
∵c = vλ ∴ λ = \(\frac{c}{v}\)
जहाँ λ विद्युत् चुम्बकीय विकिरण की तरंगदैर्ध्य एवं v आवृत्ति है।
इस फोटॉन का गतिक द्रव्यमान
m = \(\frac{h}{c \lambda}\)
∴ फोटॉन का संवेग
\(p=m c=\frac{h}{c \lambda} \times c=\frac{h}{\lambda}\)
∴फोटॉन की डी-ब्रॉग्ली तरंगदैर्ध्य
\(\lambda^{\prime}=\frac{h}{p}=\frac{h}{h / \lambda}=\lambda^{\circ}\)
या λ' = λ
अर्थात् फोटॉन की डी - ब्रॉग्ली तरंगदैर्ध्य = विकिरण की तरंगदैर्ध्य

प्रश्न 19.
वायु में 300 K ताप पर एक नाइट्रोजन अणु की डी - बॉग्ली तरंगदैर्ध्य कितनी होगी? यह मान लीजिए कि अणु इस ताप पर अणुओं की वर्ग - माध्य - मूल चाल (root mean square) से गतिमान है। (नाइट्रोजन का परमाणु द्रव्यमान - 14:0076 u)।
हल: 
दिया है: T= 300 K,
नाइट्रोजन के एक अणु का द्रव्यमान
m = 2 x 14.0076 u
= 2 x 14.0076 x 1.67 x 10^-27 kg
= 46.78 x 10^-27 kg
क्योंकि lu= 1.67 x 10^-27 kg
यदि अणु की वर्ग - माध्य - मूल चाल है तो 
1 अणु की गतिज ऊर्जा

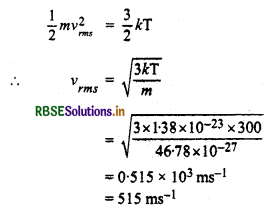
नाइट्रोजन अणु की डी - ब्रॉग्ली तरंगदैर्ध्य
\(\lambda=\frac{h}{m v_{r m s}}=\frac{6.62 \times 10^{-34}}{46.78 \times 10^{-27} \times 515}\)
= 2.75 x 10^-11 m
= 0.0275 x 10^-9 m
= 0.028 m

प्रश्न 20.
(a) एक निर्वात नली के तप्त कैथोड (heated cathode) से उत्सर्जित इलेक्ट्रॉनों की उस चाल का आकलन कीजिए, जिससे वे असर्जक की तुलना में 500 V के विभवान्तर पर रखे गये ऐनोड से टकराते हैं। इलेक्ट्रॉनों की लघु प्रारम्भिक (initial speeds) चालों की उपेक्षा (Ignore) कर दें। इलेक्ट्रॉन का आपेक्षिक आवेश अर्थात् \(\frac{e}{m}=1.76 \times 10^{11} \mathrm{C} \mathrm{kg}^{-1} \)है।
(b) संग्राहक विभव (collector potential) 10 MV के लिए इलेक्ट्रॉनों की चाल ज्ञात करने के लिए उसी सूत्र का प्रयोग करें, जो (a) में काम लाया गया है। क्या आप इस सूत्र को गलत पाते हैं? इस सूत्र को किस प्रकार सुधारा जा सकता है?
हल: 
(a) दिया है: त्वरक विभव V = 500 V 
इलेक्ट्रॉनों का आपेक्षिक आवेश
\(\frac{e}{m}=1.76 \times 10^{11} \mathrm{C} \mathrm{kg}^{-1}\)
यदि ऐनोड से टकराते समय इलेक्ट्रॉन का वेग v मान लें तो

(b) पुन: जब V = 10MV = 10 x 10⁶ V = 10⁷ V
अत: भाग (a) के सूत्र के प्रयोग से,
\(\begin{aligned} v &=\sqrt{2 \times \frac{e}{m} \times V} \\ &=\sqrt{2 \times 1.76 \times 10^{11} \times 10^7} \\ &=1.876 \times 10^9 \\ &=18.76 \times 10^8 \mathrm{~ms}^{-1} \end{aligned}\)
∵ प्राप्त वेग v > c (निर्वात् में प्रकाश की चाल) 
यह सम्भव नहीं है, अतः इस दशा में उक्त सूत्र सही नहीं है।
इस दशा में इलेक्ट्रॉन की सही चाल ज्ञात करने के लिए सापेक्षता के विशिष्ट सिद्धान्त का उपयोग करना होगा। इस सिद्धान्त के अनुसार जब कोई कण प्रकाश के वेग के तुलनीय वेग से गति करता है तो गतिज अवस्था में उसका द्रव्यमान
\(m=\frac{m_0}{\sqrt{1-v^2 / c^2}}\)
जहाँ m₀ = कण का विराम द्रव्यमान
अतः कण की गतिज ऊर्जा में वृद्धि निम्नलिखित सूत्र से प्राप्त होगी-
\(\Delta m \cdot c^2=\mathrm{V} . e\)

या (m - m₀) c² = V.e

 

प्रश्न 21. 
(a). एक समोजी (monoenergetic) (समान ऊर्जा वाले) इलेक्ट्रॉन किरण पुंज जिसमें इलेक्ट्रॉन की चाल 5.20 x 10⁶ ms^-1 है, पर एक चुम्बकीय क्षेत्र 1.30 x 10^-4 T किरण पुंज की चाल
के लम्बवत् लगाया जाता है। किरण पुंज द्वारा आरेखित वृत्त की त्रिज्या कितनी होगी, यदि \(\frac{e}{m}\) का मान 1.76 x 10¹¹ C kg^-1 है।
(b) क्या जिस सूत्र को (क) में उपयोग में लाया गया है वह यहाँ भी एक 20 MeV इलेक्ट्रॉन किरण पुंज की त्रिज्या परिकलित करने के लिए युक्तिपरक है? यदि नहीं तो किस प्रकार इसमें संशोधन (modified) किया जा सकता है?
[नोट-प्रश्न 20 (b) तथा 21 (b) आपको आपेक्षिकीय यान्त्रिकी तक ले जाते हैं जो इस पुस्तक के विषय के बाहर है। यहाँ पर इन्हें इस बिन्दु पर बल देने के लिए सम्मिलित किया गया है कि जिन सूत्रों को आप (a) में उपयोग में लाते हैं वे बहुत उच्च चालों अथवा ऊर्जाओं पर युक्तिपरक नहीं होते।]
हल: 
(a) दिया है: \(\frac{e}{m_0}\) = 1.76 x 10¹¹ C kg^-1, B = 1.30 x 10^-4 T, v = 5.20 x 10⁶ ms^-1
चूँकि चुम्बकीय क्षेत्र इलेक्ट्रॉन पुंज के लम्बवत् लगाया गया है अत: इलेक्ट्रॉनों का मार्ग वृत्ताकार होगा। इस वृत्तीय मार्ग को त्रिज्या
r = \(\frac{m_0 v}{e \mathrm{~B}}=\frac{m_0}{e} \times \frac{v}{\mathrm{~B}}\)
या r = \(\frac{1}{\left(e / m_o\right)} \times \frac{v}{\mathrm{~B}}\)
= \(\frac{1}{1.76 \times 10^{11}} \times \frac{5.20 \times 10^6}{1.30 \times 10^{-4}}\)
= 2.27 x 10^-1
= 22.7 x 10^-2 m
= 22.7 cm

(b) यहाँ इलेक्ट्रॉन की ऊर्जा
\(\frac{1}{2} m_0 v^2=20 \mathrm{MeV}=20 \times 10^6 \mathrm{eV}\)
= 20 x 10⁶ x e जूल

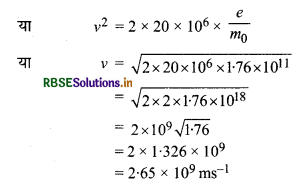
∵ इलेक्ट्रॉन की यह चाल निर्वात् में प्रकाश की चाल (c) से अधिक है। ऐसा सम्भव नहीं है। अत: पथ की त्रिज्या का परिकलन करने के लिए सामान्य सूत्र का प्रयोग नहीं किया जा सकता है। इसके लिए हमें आपेक्षिक यान्त्रिकी (relativistic mechanics) का प्रयोग करना होगा।
अत: त्रिज्या के सूत्र\( r = \frac{m_0 v}{e \mathrm{~B}}\) में m₀ के स्थान पर इलेक्ट्रॉन का गतिक द्रव्यमान m रखना होगा जो निम्न सूत्र से मिलता है-

इस सूत्र का उपयोग करके पथ की त्रिज्या की गणना की जा सकती है।

प्रश्न 22. 
एक इलेक्ट्रॉन गन जिसका संग्राहक (collector) 100 V विभव पर है, एक कम दाब (~10^-2 mm पारा) पर हाइड्रोजन से भरे गोलाकार बल्ब में इलेक्ट्रॉन छोड़ती है। एक चुम्बकीय - क्षेत्र जिसका मान 2.83 x 10^-4 T है, इलेक्ट्रॉन के मार्ग को 12.0 cm त्रिज्या के वृत्तीय कक्षा में वकित कर देता है। (इस मार्ग को देखा जा सकता है क्योंकि मार्ग में गैस आयन किरण पुंज के इलेक्ट्रॉनों को आकर्षित करके और इलेक्ट्रॉन ग्रहण करके प्रकाश उत्सर्जन करके फोकस करते हैं, इस विधि को 'परिष्कृत किरण - पुंज नली' विधि कहते हैं।) आँकड़ों से \(\frac{e}{m}\) का मान निर्धारित कीजिए।
हल: 
दिया है: इलेक्ट्री का त्वरक विभव V = 100 V, B = 2.83 x 10^-4 T, वक़ पथ की त्रिज्या r = 12.0 cm = 0.12 m 
∵ इलेक्ट्रॉनों की गतिज ऊर्जा
\(\frac{1}{2} m v^2 \)= V.e जूल
∴ \(v=\sqrt{\frac{2 \mathrm{~V} . e}{m}}\)
∵ इलेक्ट्रॉनों के वक्र पथ की त्रिज्या

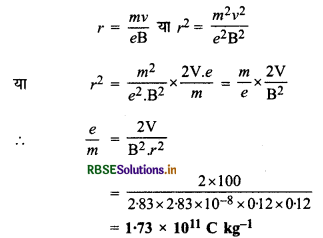
प्रश्न 23.
(a) एक X - किरण नली विकिरण का एक संतत स्पेक्ट्रम (continuous spectrum) जिसका लघु तरंगदैर्घ्य सिरा 0.45 A पर है, उत्पन्न करता है। विकिरण में किसी फोटॉन की उच्चतम ऊजां कितनी
(b) अपने (a) के उत्तर से अनुमान लगाइए कि किस कोटि की त्वरक वोल्टता (इलेक्ट्रॉन के लिए) की इस नली में आवश्यकता है?
हल: 
(a) दिया है: λ_min = 0.45 Å = 0.45 x 10^-10 m
विकिरण में फोटॉन की अधिकतम ऊर्जा

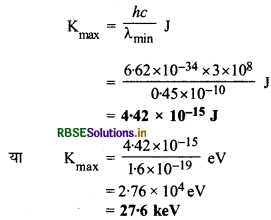
(b) जब इलेक्ट्रॉन की समस्त ऊर्जा X - किरण फोटॉन में बदल जाती है तो न्यूनतम तरंगदैर्ध्य की X - किरणें प्राप्त होती हैं।
∴ \(\mathrm{K}_{\max }=\mathrm{Ve}\)
या \(\mathrm{V}=\frac{\mathrm{K}_{\max }}{e}=\frac{4.42 \times 10^{-15}}{1.6 \times 10^{-19}} \)
या V = 27.6 ke V

प्रश्न 24. 
एक त्वरित्र (accelerator) प्रयोग में पॉजिट्रॉनों (e+) के साथ इलेक्ट्रॉनों के उच्च - ऊर्जा संघट्ट पर, एक विशिष्ट घटना की व्याख्या कुल ऊर्जा 10.2 Be V के इलेक्ट्रॉन - पॉजिट्रॉन युग्म के बराबर ऊर्जा की दो γ - किरणों में विलोपन (annihilation) के रूप में की जाती है। प्रत्येक γ - किरण से सम्बन्धित तरंगदैर्यों के मान क्या होंगे? (1 BeV = 10⁹ eV)।
हल: 
विलुप्त इलेक्ट्रॉन - पॉजिट्रॉन युग्म की कुल ऊर्जा
= 10.2 x 10⁹ eV
यह ऊर्जा दो γ - फोटॉनों में बराबर - बराबर बँट जाती है अत: प्रत्येक फोटॉन की ऊर्जा
\(\begin{aligned} E &=\frac{1}{2} \times 10 \cdot 2 \times 10^9 \mathrm{eV} \\ &=5 \cdot 1 \times 10^9 \times 1.6 \times 10^{-19} \mathrm{~J} \\ &=8.16 \times 10^{-10} \mathrm{~J} \end{aligned}\)
∵ \(\mathrm{E}=\frac{h c}{\lambda} \Rightarrow \lambda=\frac{h c}{\mathrm{E}}\)
∴ \(\lambda=\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{8.16 \times 10^{-10}}\)
= 2.43 x 10^-16 m

प्रश्न 25. 
आगे आने वाली दो संख्याओं का आकलन रोचक हो सकता है। पहली संख्या यह बतायेगी कि रेडियो अभियांत्रिक (radio engineering) फोटॉन की अधिक चिन्ता क्यों नहीं करते। दूसरी संख्या आपको यह बतायेगी कि हमारे नेत्र 'फोटॉनों की गिनती' क्यों नहीं कर सकते? भले ही प्रकाश साफ - साफ संसूचन (detection) योग्य हो।
(a) एक मध्य तरंग (medium wave) 10 kW सामर्थ्य के प्रेषी (transmitter),जो 500 m तरंगदैर्य की रेडियो तरंग उत्सर्जित करता है, के द्वारा प्रति सेकण्ड उत्सर्जित फोटॉनों की संख्या।
(b) निम्नतम तीव्रता का श्वेत प्रकाश जिसे हम देख सकते हैं (perceive) (~10^-10 Wm^-2 ) के संगत फोटॉनों की संख्या जो प्रति सेकण्ड हमारे नेत्रों की पुतली (pupil) में प्रवेश करती है। पुतली का क्षेत्रफल लगभग 0.4 cm² और श्वेत प्रकाश की औसत आवृत्ति को लगभग 6 x 10¹⁴ Hz मानिए। 
हल: 
(a) प्रेषी की शक्ति
P = 10 kW = 10 x 10³ W = 10⁴ W
t = 1 sec, λ = 500 m
प्रेषी द्वारा 1 sec में उत्सर्जित विकिरण ऊर्जा
Q = P जूल = 10⁴ W
एक फोटॉन की ऊर्जा
\(\begin{aligned} \mathrm{E}=\frac{h c}{\lambda} &=\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{500} \mathrm{~J} \\ &=3.98 \times 10^{-28} \mathrm{~J} \end{aligned} \)
यदि स्रोत से प्रति सेकण्ड उत्सर्जित फोटॉनों की संख्या = n हो तो 
Q = n.E
∴ \(n=\frac{Q}{E}=\frac{10^4}{3.98 \times 10^{-28}}\)
= 0.251 x 10³²
n = 2.51 x 10³¹ फोटॉन प्रति सेकण्ड 
स्पष्ट है कि 10 kW के प्रेषी द्वारा प्रति सेकण्ड उत्सर्जित फोटॉनों की संख्या इतनी अधिक है। अत: फोटॉनों की अलग - अलग ऊर्जा की उपेक्षा करके रेडियो तरंगों की कुल ऊर्जा को सतत् माना जा सकता है। 

(b) श्वेत प्रकाश की औसत आवृत्ति
v = 6 x 10¹⁴ Hz
∵ एक फोटॉन की ऊर्जा
E = hv = 6.62 x 10^-34 x 6 x 10¹⁴ J
= 39.72 x 10^-20J
= 3.97 x 10^-19 J
आँख द्वारा संसूचित न्यूनतम तीव्रता = 10^-10 Wm^-2
∴ आँख में प्रवेश करने वाले प्रकाश की न्यूनतम शक्ति 
Pmin = आँख द्वारा संसूचित न्यूनतम तीव्रता x पुतली का क्षेत्रफल 
= 10^-10 Wm^-2 x (0.4 x 10^-4 m²) 
= 0.4 x 10^-14 W
= 4 x 10^-15 W
अत: आँख में प्रति सेकण्ड प्रवेश करने वाले फोटॉनों की संख्या
\(n=\frac{\mathrm{P}_{\min }}{\mathrm{E}}=\frac{4 \times 10^{-15}}{3.97 \times 10^{-19}}\)
= 104 फोटोंन/सेकण्ड 
यद्यपि आँख में प्रति सेकण्ड प्रवेश करने वाले फोटॉनों की यह संख्या प्रेषी से प्रति सेकण्ड उत्सर्जित फोटॉनों की संख्या से काफी कम है परन्तु आँख के सूक्ष्म क्षेत्रफल की दृष्टि से इतनी अधिक है कि हम आँख पर गिरने वाले फोटॉनों के अलग - अलग प्रभाव को संसूचित (detect) नहीं कर पाते हैं बल्कि प्रकाश के सतत् प्रभाव का अनुभव करते हैं।

प्रश्न 26. 
एक 100 w पारद (Mercury) खोत से उत्पन्न 2271 Å तरंगदैर्घ्य का पराबैंगनी प्रकाश एक मॉलिब्डेनम धातु से निर्मित प्रकाश सेल को विकिरित (radiate) करता है। यदि निरोधी विभव - 1.3 V हो तो धातु के कार्य - फलन का आंकलन कीजिए। एक He - Ne लेसर द्वारा उत्पन्न 6328 Å के उच्च तीव्रता(~ 10⁵ Wm^-2)केलाल प्रकाश के साथ प्रकाश सेल किस प्रकार अनुक्रिया करेगा?
हल: 
दिया है: λ₁ = 2271 Å = 2271 x 10^-10 m, V₀ = -1.3 V, e = -1.6 x 10^-19 C, कार्य - फलन \phi_0 = ? 
आपतित फोटॉन की ऊर्जा
\(\begin{aligned} E &=\frac{h c}{\lambda_1}=\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{2271 \times 10^{-10}} \mathrm{~J} \\ &=8.745 \times 10^{-19} \mathrm{~J} \end{aligned}\)
प्रकाश इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा

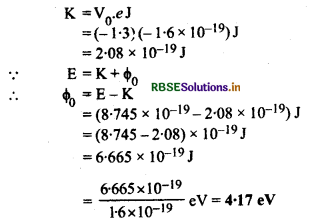
यदि देहली तरंगदैर्ध्य λ₀ हो तो
\(\phi_0=\frac{h c}{\lambda_0} \Rightarrow \lambda_0=\frac{h c}{\phi_0}\)
या \(\lambda_0=\frac{6 \cdot 62 \times 10^{-34} \times 3 \times 10^8}{6.665 \times 10^{-19}}\)
= 2.979 x 10^-7 m
= 2979 x 10^-10 m = 2979 Å
∵ दिया है: λ₂ = 6328 Å
∴ λ₂ > λ₀
अत: प्रकाश सेल इलेक्ट्रॉनों का उत्सर्जन नहीं करेगा और फलस्वरूप कोई प्रकाश - वैद्युत धारा प्रवाहित नहीं होगी।

प्रश्न 27. 
एक निऑन लैम्प से उत्पन्न 640.2 nm (1 nm =10^-9 m) तरंगदैर्घ्य का एकवर्णी विकिरण (monochromatic radiation) टंगस्टन पर सीजियम से निर्मित प्रकाश संवेदी पदार्थ को विकिरित (Irradiates) करता है। निरोथी वोल्टता 0.54 V मापी जाती है। स्त्रोत को एक लौह स्रोत से बदल दिया जाता है। इसकी 427.2 nm वर्ण रेखा उसी प्रकाश सेल को विकिरित करती है। नयी निरोधी वोल्टता ज्ञात कीजिए।
हल: 
दिया है: λ₁ = 640.2 nm = 640.2 x 10^-9 m, V_o1 = 0 54V, λ₂ = 427.2 nm = 427.2 x 10^-9 m, V_o2 = ? 
∵ आइन्स्टीन के प्रकाश वैद्युत् समीकरण से
\(e \mathrm{~V}_0=\frac{h c}{\lambda}-\phi_0\)
∴ \(e \mathrm{~V}_{0_1}=\frac{h c}{\lambda_1}-\phi_0\) ............(1)
और \(e \mathrm{~V}_{0_2}=\frac{h c}{\lambda_2}-\phi_0\) ............(2)
समी. (2) में से (1) को घटाने पर,

∴ V₀₂ = 0.97 + V₀₁ = 0.97 + 0.54
या V₀₂ = 1.51 volt

प्रश्न 28. 
एक पारद लैम्प (mercury lamp), प्रकाश - विद्युत् उत्सर्जन की आवृत्ति निर्भरता के अध्ययन के लिए एक सुविधाजनक स्त्रोत है, क्योंकि यह दृश्य - स्पेक्ट्रम के पराबैंगनी (UV) से लाल छोर तक कई वर्ण - रेखाएँ (speetral lines) असर्जित करता है। रूबीडियम प्रकाश सेल के हमारे प्रयोग में, पारद (Mercury) खोत की विभिन्न निम्न वर्ण रेखाओं का प्रयोग किया गया-
λ₁ = 3650 Å, λ₂ = 4047 Å, λ₃ = 4358 Å, λ₄ = 5461 Å, λ₅ = 6907 Å के लिए निरोधी वोल्टताएँ, क्रमशः निम्नलिखित पायी गई है-
V_o1 = 1.28 V, V_o2 = 0.95 V, V_o3 = 0.74 V, V₀₄ = 0.16 V, V_o5 = 0 V.
(a) प्लांक नियतांक का मान ज्ञात कीजिए।
(b) धातु के लिए देहली आवृत्ति तथा कार्य - फलन का आकलन कीजिए। [नोट-उपर्युक्त आँकड़ों से h का मान ज्ञात करने के लिए आपको e = 1.6 x 10^-19 C की आवश्यकता होगी। इस प्रकार के प्रयोग Na, Li, K आदि के लिए मिलिकन ने किये थे। मिलिकन ने अपने तेल - बंद प्रयोग से प्राप्त e के गन का उपयोग कर आइन्स्टीन के प्रकाश - वैद्युत समीकरण को सत्यापित किया तथा इन्हीं प्रेक्षणों से। के मान के लिए पृथक् अनुमान लगाया।] 
हल: 
∵ किसी तरंगदैर्ध्य λ एवं संगत आवृत्ति v में सम्बन्ध
\(c=v \lambda \quad \therefore v=\frac{c}{\lambda}\)

इस प्रकार आवृत्ति (v) एवं निरोधी विभव (V₀) को निम्न प्रकार सारणीबद्ध किया जा सकता है-

आवृत्ति (v)	8.2 x 1014 Hz	7.4 x 1014 Hz	6.9 x 1014 Hz	5.5 x 1014 Hz	4.3 x 1014 Hz
निरोधी विभव (V0)	1.28 V	0.95 V	0.74 V	0.16 V	0.0 V

इन आँकड़ों से v व V₀ के मध्य खींचा गया ग्राफ निम्न चित्र के अनुसार होगा-

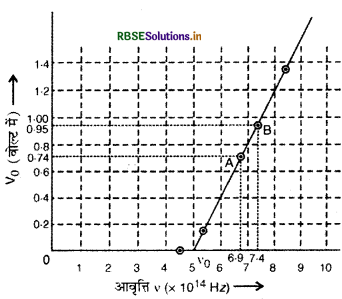
उक्त ग्राफ से स्पष्ट है कि ग्राफ एक सरल रेखा है जो आवृत्ति की अक्ष को 5 x 10¹⁴ Hz आवृत्ति पर काटती है। अत: देहली आवृत्ति v₀ = 5.0 x 10¹⁴ Hz पाँचवें बिन्दु के लिए v < v₀ है अतः इसके संगत निरोधी विभव
(a) हम जानते हैं कि (V0 - v) वक्र की प्रवणता ही प्लांक नियतांक के बराबर होती है अतः 
सूत्र ∵ V_o.e = hv - \(\phi_0\) से,
\(\mathrm{V}_{0_1} \cdot e=h \mathrm{v}_1-\phi_0\)
और \(\mathrm{V}_{0_2} \cdot e=h v_2-\phi_0 \)
अत: \(\left(\mathrm{V}_{0_2}-\mathrm{V}_{0_1}\right) \cdot e=h\left(v_2-v_1\right)\)
⇒ \(\Delta \mathrm{V}_0 \cdot e=h \cdot \Delta \mathrm{v}\)
∴ \(h=\frac{e \cdot \Delta \mathrm{V}_0}{\Delta v}\)
ग्राफ से बिन्दु A के संगत v₁ = 6.9 x 10¹⁴ Hz 
और V_o1 = 0.74 V 
और बिन्दु B के संगत v₂ = 7.4 x 10¹⁴ Hz 
और V_o2 = 0.95 V
∴ \(\begin{aligned} \Delta \mathrm{V}_0 &=\mathrm{V}_{0_2}-\mathrm{V}_{0_1} \\ &=0.95-0.74 \\ &=0.21 \mathrm{~V} \end{aligned}\)
और \(\begin{aligned} \Delta v &=v_2-v_1 \\ &=(7 \cdot 4-6 \cdot 9) \times 10^{14} \\ &=0 \cdot 5 \times 10^{14} \mathrm{~Hz} \end{aligned}\)
अत: \(h=\frac{e . \Delta \mathrm{V}_0}{\Delta v}=\frac{1.6 \times 10^{-19} \times 0.21}{0.5 \times 10^{14}}\)
\(=\frac{0.336}{0.5} \times 10^{-33} \mathrm{~J}-\mathrm{s}=0.672 \times 10^{-33} \mathrm{~J}-\mathrm{s}\)
या h = 6.7 x 10^-34 Js

(b) ग्राफ से देहली आवृत्ति v₀ = 5.0 x 10¹⁴ Hz 
कार्य - फलन \phi_0 = hv₀ = 6.7 x 10^-34 x 5 x 10¹⁴
= 33.5 x 10^-20J
= 3.35 x 10^-19 J
या \(\phi_0=\frac{3.35 \times 10^{-19}}{1.6 \times 10^{-19}} \mathrm{eV}\)
= 2.09 eV = 2.1 eV

प्रश्न 29. 
निम्न धातुओं के कार्य - फलन निम्न प्रकार दिये गये हैं-
Na : 2.75 eV, K : 2.30 eV, Mo : 4.17 eV, Ni : 5.15 eV
इन धातुओं में से कौन प्रकाश सेल से 1 m दूर रखे गये He - Cd लेसर से अपन्न 3300 Å तरंगदैर्ध्य के विकिरण के लिए प्रकाश - वैद्युत उत्सर्जन नहीं देगा? लेसर को सेल के निकट 50 m दूर रखने पर क्या होगा?
हल: 
दिया है: लेसर से उत्पन्न प्रकाश की तरंगदैर्घ्य λ = 3300 Å = 3.3 x 10^-7 m.
इस विकिरण के एक फोटॉन की ऊर्जा
\(\begin{aligned} \mathrm{E} &=\frac{h c}{\lambda} \mathrm{J}=\frac{h c}{\lambda . e} \mathrm{eV} \\ &=\frac{6.6 \times 10^{-34} \times 3 \times 10^8}{3.3 \times 10^{-7} \times 1.6 \times 10^{-19}} \mathrm{eV} \\ &=3.75 \mathrm{eV} \end{aligned}\)
Mo व Ni के लिए E < \(\phi_0\)
अतः इन दोनों धातुओं से इलेक्ट्रॉन उत्सर्जित नहीं होंगे।
लेसर की दूरी 1 m से घटाकर 50 cm कर देने पर उत्सर्जित इलेक्ट्रॉनों की संख्या तो बढ़ जायेगी क्योंकि फोटो सेल पर गिरने वाले प्रकाश की तीव्रता बढ़ जायेगी लेकिन प्रकाश इलेक्ट्रॉनों की गतिज ऊर्जा पर कोई प्रभाव नहीं होगा।

प्रश्न 30.
10^-5 Wm^-2 तीव्रता का प्रकाश सोडियम प्रकाश सेल के 2 cm² क्षेत्रफल के पृष्ठ पर पड़ता है। यह मान लें कि ऊपर की सोडियम की पाँच परतें (layers) आपतित ऊर्जा को अवशोषित (absorbed) करती हैं तो विकिरण के तरंग - चित्रण में प्रकाश - विद्युत् असर्जन के लिए आवश्यक समय का आंकलन (estimate) कीजिए। धातु के लिए कार्य - फलन लगभग 2eV दिया गया है। आपके उत्तर का क्या निहितार्थ (implication) है?
हल: 
दिया है: प्रकाश की तीव्रता
I = 10^-5 Wm^-2 
सेल का क्षेत्रफल
A = 2cm = 2 x 10^-4 m²; \phi_0 = 2 eV 
सोडियम परमाणु की लगभग प्रिज्या
r = 10^-10 m 
∴ सोडियम परमाणु का लगभग क्षेत्रफल
= πr² = 3.14 x 10^-20 m² ≈ 10^-20 m²
∴ एक परत में मौजूद सोडियम परमाणुओं की संख्या

\(=\frac{2 \times 10^{-4}}{10^{-20}}=2 \times 10^{16}\)
∴ 5 परतों में परमाणुओं की संख्या
n = 5 x 2 x 10¹⁶ = 10¹⁷ 
∵ सोडियम परमाणु में एक चालन इलेक्ट्रॉन होता है, अत: सोडियम को सभी परतों में n इलेक्ट्रॉन होंगे। 
सेल पर प्रति सेकण्ड आपतित प्रकाश ऊर्जा
= I x A
= 10^-5 x 2 x 10^-4 = 2 x 10^-9 W
∵ कुल ऊर्जा सोडियम की पाँच परतों द्वारा अवशोषित (absorbed) होती हैं अतः तरंग सिद्धान्त के अनुसार यह ऊर्जा पाँचों परतों में समान रूप से बँट जायेगी।
∴ एक इलेक्ट्रॉन को प्रति सेकण्ड मिलने वाली ऊर्जा
\(=\frac{2 \times 10^{-9}}{10^{17}}=2 \times 10^{-26} \mathrm{Js}^{-1}\)
∵ कार्य - फलन \(\phi_0=2 \mathrm{eV}=2 \times 1.6 \times 10^{-19} \mathrm{~J}\)
= 3.2 x 10^-19 J
अर्थात् एक इलेक्ट्रॉन को उत्सर्जित करने के लिए आवश्यक ऊर्जा = 3:2 x 10^-19 J
∴ किसी इलेक्ट्रॉन को उत्सर्जित होने में लगा समय 
t = आवश्यक ऊर्जा (कार्य - फलन) प्राप्त करने में लगा समय
\(=\frac{3 \cdot 2 \times 10^{-19}}{2 \times 10^{-26}}=1.6 \times 10^7 \mathrm{~s}\)
या \(=\frac{1.6 \times 10^7}{365 \times 24 \times 60 \times 60}\) वर्ष
\(=\frac{160000}{365 \times 24 \times 36}\)
= 0.5037 वर्ष
= 0.5 वर्ष 
उत्तर का निहितार्थ: इस उत्तर से स्पष्ट है कि तरंग सिद्धान्त के अनुसार एक इलेक्ट्रॉन के उत्सर्जन में लगा समय अत्यधिक (0.5 वर्ष) है जो प्रेक्षित समय (~10^-9 s) से बिल्कुल मेल नहीं खाता है। अतः यह तथ्य स्पष्ट हो जाता है कि प्रकाश - वैद्युत प्रभाव की व्याख्या करने में तरंग सिद्धान्त पूर्णतः असफल है।

प्रश्न 31.
X - किरणों के प्रयोग अथवा उपयुक्त वोल्टता से त्वरित इलेक्ट्रॉनों से क्रिस्टल विवर्तन प्रयोग किये जा सकते हैं। कौन - सी जाँच (which probe) अधिक ऊर्जा सम्बद्ध है? [परिमाणिक तुलना (quantitative comparison) के लिए, जाँच के लिए तरंगदैयं को 1 Å लीजिए, जो कि जालक (लैटिस) में अन्तर - परमाणु अन्तरण (Interatomic spacing) की कोटि का है] दिया है-
me = 9.11 x 10^-31 kg
हल:
X - किरणं फोटॉनों की तरंगदैष्य
λ = 1Å = 1 x 10^-10 m 
∴ एक X - किरण फोटॉन की ऊर्जा
\(\mathrm{E}=\frac{h c}{\lambda}=\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{10^{-10}} \mathrm{~J}\)
या \(\mathrm{E}=1.986 \times 10^{-15} \mathrm{~J}\)
इलेक्ट्रॉन की डी - ब्रॉग्ली तरंगदैर्ध्य
\(\lambda=\frac{h}{p} \Rightarrow p=\frac{h}{\lambda}\)
इलेक्ट्रॉन की गतिज ऊर्जा
\(\begin{aligned} \mathrm{E}^{\prime} &=\frac{1}{2} m v^2=\frac{p^2}{2 m}=\frac{h^2}{2 m \lambda^2} \\ &=\frac{6.62 \times 10^{-34} \times 6.62 \times 10^{-34}}{2 \times 9 \cdot 11 \times 10^{-31} \times 10^{-10} \times 10^{-10}} \end{aligned}\), क्योंकि यहाँ λ = 10-10 m
= 2.40 x 10-17 J
स्पष्ट है कि E > E'
अर्थात् X - किरण फोटॉन को कर्जा समान डी - ब्रॉग्ली तरंगदैर्ध्य के इलेक्ट्रॉन की गतिज ऊर्जा से अधिक होती है।

प्रश्न 32. 
(a) एक न्यूट्रॉन, जिसकी गतिज ऊर्जा 1500 eV है, की डी - ब्रॉग्ली तरंगदैर्ध्य प्राप्त कीजिए। जैसा कि आपने प्रश्न 31 में देखा है, इतनी ऊर्जा का इलेक्ट्रॉन किरण पुंज (light beam) क्रिस्टल विवर्तन प्रयोग के लिए उपयुक्त है। क्या समान ऊर्जा का एक न्यूट्रॉन किरण पुंज इस प्रयोग के लिए समान रूप से उपयुक्त होगा? स्पष्ट कीजिए। [m = 1.675 x 10^-27 kgl
(b) कमरे के सामान्य ताप (27°C) पर ऊष्मीय न्यूट्रॉन से सम्बद्ध डी - ब्रॉग्ली तरंगदैर्ध्य ज्ञात कीजिए। इस प्रकार स्पष्ट कीजिए कि क्यों एक तीव्रगामी न्यूट्रॉन को न्यूट्रॉन - विवर्तन प्रयोग में उपयोग में लाने से पहले वातावरण के साथ तापीकृत (thermolised) किया जाता है।
हल: 
(a) डी - बॉग्ली तरंगदैर्ध्य, \(\lambda=\frac{h}{\sqrt{2 m K}} \)
यहाँ K = 150 eV = 150 x 1.6 x 10^-19 J
= 2.4 x 10^-17 J
∴ λ = \(\frac{6.63 \times 10^{-34}}{\sqrt{2 \times 1.675 \times 10^{-27} \times 2.4 \times 10^{-17}}} m\)
= \(\frac{6.63 \times 10^{-34}}{2.835 \times 10^{-22}}\)
= 2.338 x 10^-12 m
= 0.02338 Å 

चूँकि क्रिस्टल में तलों के बीच की दूरी इस तरंगदैर्ध्य से लगभग 100 गुनी अधिक है। अतः न्यूट्रॉन पुंज क्रिस्टल से विवर्तित नहीं होगा बल्कि सीधा ही क्रिस्टल से गुजर जायेगा।

(b) तापीय न्यूट्रॉनों (Thermalneutrons) से बद्ध डी - ब्रॉग्ली तरंगदैर्ध्य,
\(\lambda=\frac{h}{\sqrt{3 m k \mathrm{~T}}}\)
यहाँ T = 273 + 27 = 300 K, k = 1.38 x 10^-23 JK^-1, mn = 1.675 x 10^-27 kg
∴ \(\lambda=\frac{6.63 \times 10^{-34}}{\sqrt{3 \times 1.675 \times 10^{-27} \times 1.38 \times 10^{-23} \times 300}}\)
\(\begin{aligned} &=1.4539 \times 10^{-10} \mathrm{~m} \\ &=\mathbf{1 \cdot 4 5} \AA \end{aligned}​​\)
यह क्रिस्टल में अन्तरापरमाण्विक दूरी से तुलनीय है। अतः तापीय न्यूट्रॉन क्रिस्टल द्वारा विवर्तित हो सकते हैं। उच्च ऊर्जा के न्यूट्रॉन की तरंगदैर्ध्य बहुत कम होती है। अत: वे क्रिस्टल से बिना विवर्तित हुए गुजर जायेंगे। यही कारण है कि तीव्रगामी न्यूट्रॉन पुंज को विवर्तन प्रयोग में प्रयुक्त करने से पहले उसे परिवेश के साथ तापीकृत किया जाता है।

प्रश्न 33. 
एक इलेक्ट्रॉन सूक्ष्मदर्शी में 50 kV वोल्टता के द्वारा त्वरित इलेक्ट्रॉनों का उपयोग किया जाता है। इन इलेक्ट्रॉनों से जुड़े डी - शॉग्ली तरंगदैर्ध्य का मान ज्ञात कीजिए। यदि अन्य बातों (जैसे कि संख्यात्मक द्वारक (numerical aperture) आदि) को लगभग समान लिया जाये, इलेक्ट्रॉन सूक्ष्मदर्शी की विभेदन क्षमता (resolving power) की तुलना पीले प्रकाश का प्रयोग करने वाले प्रकाश सूक्ष्मदर्शी से किस प्रकार होती है? 
हल: 
दिया है:
V = 50 kV = 50 x 10³ V = 5 x 10⁴ V 
∴ इलेक्ट्रॉन की ऊर्जा
E = Ve जूल 
या \(\frac{1}{2} m v^2=V e\)
या \(v=\sqrt{\frac{2 \mathrm{Ve}}{m}}\)
अत: इलेक्ट्रॉनों का संवेग
\(p=m v=m \sqrt{\frac{2 \mathrm{Ve}}{m}}=\sqrt{2 m \mathrm{~V} . e}\)
अतः इलेक्ट्रॉनों को डी - ब्रॉग्ली तरंगदैर्ध्य

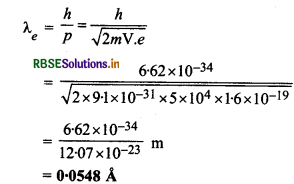
पोले प्रकाश की तरंगदैर्ध्य λ_y = 5900 Å
∵ प्रकाशिक यन्त्र को विभेदन क्षमता\( \propto \frac{1}{\lambda}\)

\(=\frac{\lambda_y}{\lambda_e}=\frac{5900 \AA}{0.0548 \AA}=\mathbf{1 . 0 8} \times 10^5\)
स्पष्ट है कि इलेक्ट्रॉन सूक्ष्मदर्शी की विभेदन अमता प्रकाशिक सूक्ष्मदर्शी की विभेदन क्षमता की 105 गुनी होती है।

प्रश्न 34. 
किसी जाँच की तरंगदैर्ध्य उसके द्वारा कुछ विस्तार में जाँच की जा सकने वाली संरचना के आकार की लगभग आमाप (roughly measure) है। प्रोटॉनों तथा न्यूट्रॉनों की क्वार्क (quark) संरचना 10^-15 m या इससे भी कम लम्बाई के लघु पैमाने की है। इस संरचना को सर्वप्रथम 1970 दशक के प्रारम्भ में, एक रेखीय त्वरित्र (linear accelerator) से उत्पन्न उच्च ऊर्जा इलेक्ट्रॉनों के किरण - पुंजों के उपयोग द्वारा, स्टैनफोर्ड, संयुक्त राज्य अमेरिका में जांचा गया था। इन इलेक्ट्रॉन किरण पुंजों की ऊर्जा की कोटि का अनुमान लगाइए। (इलेक्ट्रॉन की विराम दव्यमान ऊर्जा 0.511 Mev है।)
हल: 
क्वार्क संरचना का आमाप, λ = 10^-15 m 
इलेक्ट्रॉन का विराम दव्यमान m0 = 9.1 x 10^-31 kg 
∴ इलेक्ट्रॉन की विराम द्रव्यमान ऊर्जा
\(\begin{aligned} \mathrm{E}_0 &=m_0 \cdot c^2 \\ &=9 \cdot 1 \times 10^{-31} \times 3 \times 10^8 \times 3 \times 10^8 \mathrm{~J} \\ &=81.9 \times 10^{-15} \mathrm{~J} \\ &=8 \cdot 19 \times 10^{-14} \mathrm{~J} \end{aligned}\)
∵ डी - ब्रॉग्ली तरंगदैर्ध्य\( \lambda=\frac{h}{p}\)
संवेग \(p=\frac{h}{\lambda}\)
या \(p=\frac{6.62 \times 10^{-34}}{10^{-15}}=6.62 \times 10^{-19} \mathrm{~J}\)
∵ आपेक्षिकता के सिद्धान्त से,
E² = m₀²c⁴ + p²c²
= (m₀c²)² + p²c²
= (8.19 x 10^-14)² + (6.62 x 10^-19)² (3 x 10⁸)²
= 67.076 x 10^-28 + 43.824 x 10^-38 x 9 x 10¹⁶
= 6.707 x 10^-28 + 3.94 x 10^-20
\(\approx 3.94 \times 10^{-20}\) , क्योंकि (6.707 x10^-28) बहुत छोटी राशि है अतः इसे छोड़ने पर 
∴ \(\mathrm{E}=\sqrt{3.94 \times 10^{-20}}=1.98 \times 10^{-10} \mathrm{~J}\)
\(\begin{aligned} &=\frac{1.98 \times 10^{-10}}{1.6 \times 10^{-19}} \mathrm{eV} \\ &=1.24 \times 10^9 \mathrm{eV} \end{aligned}\)
अत: रेखीय त्वरित्र (linear accelerator) से निर्गत् इलेक्ट्रॉनों की ऊर्जा 10⁹ eV या BeV की कोटि की है।

प्रश्न 35. 
कमरे के ताप (27° C) और 1 वायुमण्डलीय दाब पर He परमाणु से जुड़े प्रारूपी डी - ब्रॉग्ली तरंगदैर्घ्य ज्ञात कीजिए और इन परिस्थितियों (these conditions) में इसकी तुलना दो परमाणुओं के बीच औसत दूरी से कीजिए। 
हल: 
दिया है: T = 27 + 273 = 300K, P = 1.01 x 10⁵ Nm^-2
ऐवोगैडो संख्या N = 6.02 x 10²³ प्रति ग्राम अणु 
∴ एक हीलियम परमाणु का द्रव्यमान
\(\begin{aligned} m &=\frac{\mathrm{M}}{\mathrm{N}}=\frac{4 \mathrm{gm}}{6.02 \times 10^{23}} \\ &=\frac{4}{6.02} \times 10^{-23} \\ &=0.667 \times 10^{-23} \\ &=6.67 \times 10^{-24} \mathrm{gm} \\ &=6.67 \times 10^{-27} \mathrm{~kg} \end{aligned}\)
∵ \(\mathrm{E}=\frac{1}{2} m v^2=\frac{3}{2} k \mathrm{~T}\)
∴ \(v=\sqrt{\frac{3 k \mathrm{~T}}{m}}\)
∴ संवेग \(p=m v=m \sqrt{\frac{3 k \mathrm{~T}}{m}}=\sqrt{3 m k \mathrm{~T}}\)
अत: डी - ब्रॉग्ली तरंगदैर्ध्य

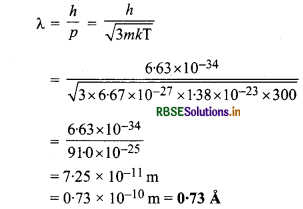
∵ एक मोल गैस के लिए गैस समीकरण
PV = N.kT 
या \(\frac{\mathrm{V}}{\mathrm{N}}=\frac{k \mathrm{~T}}{\mathrm{P}}\)
यदि परमाणुओं के मध्य दूरी r हो तो एक अणु के लिए आयतन r3 होगा।
∴ \(r^3=\frac{\mathrm{V}}{\mathrm{N}}\)
जहाँ V, एक मोल का आयतन है।
या \(r^3=\frac{k \mathrm{~T}}{\mathrm{P}}\)
∴ \(r=\left[\frac{k \mathrm{~T}}{\mathrm{P}}\right]^{1 / 3}\)
\(\begin{aligned} &=\left[\frac{1.38 \times 10^{-23} \times 300}{1.01 \times 10^5}\right]^{1 / 3} \\ &=\mathbf{3} \cdot \mathbf{4} \times 10^{-9} \mathrm{~m} \end{aligned}\)
∴ \(\frac{r}{\lambda}=\frac{0.34 \times 10^{-8}}{0.73 \times 10^{-10}}=\frac{34}{0.73}\)
या \(\frac{r}{\lambda}=46 \cdot 5\)
या r = 46.5 x λ
अर्थात् परमाणुओं के बीच की दूरी, डी - ब्रॉग्ली तरंगदैर्य से लगभग 50 गुनी बड़ी है।

प्रश्न 36. 
किसी धातु में (27°C) पर एक इलेक्ट्रॉन की प्रारूपी डी - ब्रॉग्ली तरंगदैर्ध्य परिकलित कीजिए और इसकी तुलना धातु में दो इलेक्ट्रॉनों के बीच औसत पृथक्य (average separation) से कीजिए, जो लगभग 2 x 10^-10 m दिया गया है। 
[नोट- प्रश्न 35 और 36 प्रदर्शित करते हैं कि जहाँ सामान्य परिस्थितियों में गैसीय अणुओं से जुड़े तरंग पैकेट अ - अतिव्यापी हैं, किसी धातु में इलेक्ट्रॉन तरंग पैकेट प्रबल रूप से एक - दूसरे से अतिव्यापी हैं। यह सुझाता है कि जहाँ किसी सामान्य गैस में अणुओं की अलग पहचान हो सकती है, किसी धातु में इलेक्ट्रॉन की एक-दूसरे से अलग पहचान नहीं हो सकती। इस अप्रभेद्यता की कई मूल निहितार्थताएँ हैं जिन्हें आप भौतिकी के अधिक उच्च पाठ्यक्रमों में पड़ेंगे।] 
हल: 
परम ताप T = 27 + 273 = 300 K
इस ताप पर इलेक्ट्रॉन की गतिज ऊर्जा 
\(\mathrm{E}=\frac{1}{2} m v^2=\frac{3}{2} k \mathrm{~T} \Rightarrow v=\sqrt{\frac{3 k \mathrm{~T}}{m}}\)
∴ \(p=m v=\sqrt{3 m k T}\)
अतः डी - ब्रॉग्ली तरंगदैर्ध्य
\(\lambda=\frac{h}{p}=\frac{h}{\sqrt{3 m k \mathrm{~T}}}\)
या \(\lambda=\frac{6.62 \times 10^{-34}}{\sqrt{3 \times 9.1 \times 10^{-31} \times 1.38 \times 10^{-23} \times 300}}\)
= 62 x 10^-10 m = 62 Å
दो इलेक्ट्रॉनों के मध्य दूरी r₀ = 2 x 10^-10 = 2 Å
∴ \(\frac{\lambda}{r_0}=\frac{62 \AA}{2 \AA}=31\)
λ = 31r₀
अर्थात् डी - ब्रॉग्ली तरंगदैर्ध्य इलेक्ट्रॉनों के मध्य दूरी की 31 गुनी है। 

प्रश्न 37. 
निम्नलिखित प्रश्नों के उत्तर दीजिए-
(a) ऐसा विचार किया गया है कि प्रोटॉन और न्यूट्रॉन के भीतर क्वार्क घर आंशिक (fractionmat) आवेश होते हैं \(\left[\left(+\frac{2}{3} e\right) ;\left(-\frac{1}{3} e\right)\right]\) यह मिलिकन के तेल - बूंद प्रयोग में क्यों नहीं प्रकट होते हैं?
(b) \(\frac{e}{m}\) संयोग की क्या विशिष्टता (specification) है ? हम e तथा के विषय में अलग - अलग विचार क्यों नहीं करते?
(c) गैसें सामान्य दाब पर कुचालक होती हैं, परन्तु बहुत कम दाब पर चालन प्रारम्भ कर देती हैं, क्यों?
(d) प्रत्येक धातु का एक निश्चित कार्यफलन होता है। यदि आपतित विकिरण एकवी हो तो सभी प्रकाशिक इलेक्ट्रॉन समान ऊर्जा के साथ बाहर क्यों नहीं आते हैं? प्रकाशिक इलेक्ट्रॉनों का एक ऊर्जा वितरण (energy distribution) क्यों होता है?
(e) एक इलेक्ट्रॉन की ऊर्जा तथा इसका संवेग इससे जुड़े पदार्थ-तरंग की आवृत्ति तथा इसकी तरंगदैर्ध्य के साथ निम्न प्रकार सम्बन्धित होते हैं-
\(\mathbf{E}=h v, p=\frac{h}{\lambda}\)
परन्तु λ का मान जहाँ भौतिक महत्व का है, v के मान (और इसलिए कला चालनका मान) का कोई भौतिक महत्व नहीं है, क्यों?
हल: 
(a) न्यूट्रॉन एवं प्रोटॉन के भीतर भिन्नात्मक आवेश वाले क्वार्क इस प्रकार सीमित रहते हैं कि प्रोटॉन में उपस्थित क्वाकों के आवेश का मान +e होता है और न्यूट्रॉन में उपस्थित क्वार्कों के आवेश का कुल मान शून्य रहता है। ये क्वार्क पारस्परिक आकर्षण बलों द्वारा बैंधे रहते हैं। जब इन्हें अलग करने का प्रयास किया जाता है तो बल और अधिक शक्तिशाली हो जाते हैं और इसी कारण वे एक साथ बने रहते हैं। इसीलिए प्रकृति में भिन्नात्मक आवेश मुक्त अवस्था में नहीं पाये जाते हैं, वे सदैव इलेक्ट्रॉनिक आवेश (e) के पूर्ण गुणज के रूप में ही पाये जाते हैं।

(b) इलेक्ट्रॉन की गति विभिन्न स्थितियों में विभिन्न समीकरणों जैसे eE = ma, ev = \(\frac{1}{2} m v^2, e v \mathrm{~B}=\frac{m v^2}{r}\), द्वारा निर्धारित होती है। इन
समीकरणों में \(e \text { व } m\) दोनों एक साथ आये हैं। इससे स्पष्ट है कि इलेक्ट्रॉन की गति के लिए e अथवा m पर अकेले अलग - अलग विचार करने के स्थान पर \(\frac{e}{m}\) पर विचार किया जाता है।

(c) गैसों में विद्युत चालन आयनों द्वारा होता है जो पहले से मौजूद नहीं होते बल्कि गैसों में विसर्जन (discharge) के कारण उत्पन्न होते हैं तथा उत्पन्न आयन त्वरित होकर अन्य गैस अणुओं को आयनित करके वैधुत चालन को बनाये रखते हैं। सामान्य दाब पर अणुओं के मध्य दूरी कम होती है जिससे विसर्जन से उत्पन्न आयन आयनीकरण के लिए आवश्यक ऊर्जा एकत्र होने से पूर्व ही अणुओं से टकराकर उदासीन हो जाते हैं। इसके विपरीत अत्यन्त कम दाब परास (4 mm से 10^-3 mm) में अणुओं के मध्य दूरी पर्याप्त हो जाती है और विसर्जन में उत्पन्न आयन गैस अणुओं से टकराने से आयनीकरण के लिए पर्याप्त ऊर्जा एकत्र कर लेते हैं। अत: आयनीकरण की प्रक्रिया जारी रहती है और गैसों में विद्युत् चालन होता रहता है।

(d) कार्यफलन से, चालन बैण्ड के इलेक्ट्रॉनों के उत्सर्जन के लिए आवश्यक न्यूनतम ऊर्जा का ज्ञान होता है परन्तु प्रकाश - वैद्युत उत्सर्जन में इलेक्ट्रॉन विभिन्न ऊर्जा स्तरों से निकलकर आते हैं अतः उनकी ऊर्जाएँ भिन्न - भिन्न होती हैं।

(e) किसी द्रव्य कण की ऊर्जा का निरपेक्ष (absolute) मान (न कि संवेग) एक निरपेक्ष स्थिरांक के अधीन स्वेच्छ होता है। यही कारण है कि द्रव्य तरंगों से सम्बद्ध तरंग - दैर्ध्य λ का ही भौतिक महत्व होता है न कि आवृत्ति v का। इसी कारण कला वेग vλ का भी कोई भौतिक महत्व (physical siginificance) नहीं होता है।
जबकि समूह वेग
\(\frac{d \mathrm{v}}{d\left(\frac{1}{\lambda}\right)}=\frac{d \mathrm{E}}{d p} \frac{d}{d p}\left(\frac{p^2}{2 m}\right)=\frac{p}{m}\)
भौतिक रूप से मान्य है।