RBSE Solutions for Class 12 Physics Chapter 10 तरंग-प्रकाशिकी

Rajasthan Board RBSE Solutions for Class 12 Physics Chapter 10 तरंग-प्रकाशिकी Textbook Exercise Questions and Answers.

RBSE Class 12 Physics Solutions Chapter 10 तरंग-प्रकाशिकी

RBSE Class 12 Physics तरंग-प्रकाशिकी Textbook Questions and Answers

प्रश्न 1.
589 nm तरंगदैर्य का एकवर्णीय प्रकाश वायु से जल की सतह पर आपतित होता है। (a) परावर्तित तथा (b) अपवर्तित प्रकाश की तरंगदैथ्य, आवृत्ति तथा चाल क्या होगी? जल का अपवर्तनांक 1.33 है।
उत्तर:
दिया है: आपतित प्रकाश की तरंगदैर्ध्य λ₁ = 589 nm = 589 x 10⁹ मी.
वायु में प्रकाश की चाल C = 3 x 10⁸ मीटर/सेकण्ड 
तथा \(a \mu_w=1.33\)
(a) परावर्तित प्रकाश के लिए
(i) चूंकि परावर्तित प्रकाश की तरंगदैर्ध्य परावर्तित रहती है अत: परावर्तित प्रकाश की तरंगदैर्ध्य λ_a = λ₁ = 589 nm
(ii) चूँकि परावर्तन में माध्यम नहीं बदलता अतः परावर्तित प्रकाश की चाल C = 3 x 10⁸ m/s
(ii) सूत्र C = vλ से 
परावर्तित प्रकाश की आवृत्ति \(V=\frac{C}{\lambda}\)
\(\begin{aligned} &=\frac{3 \times 10^8}{589 \times 10^{-9}} \\ &=5.093 \times 10^{14} \mathrm{~Hz} \end{aligned}\)

(b) अपवर्तित प्रकाश के लिए 
(i) यदि तरंगदैध्य λ_a हो तो

प्रश्न 2. 
निम्नलिखित दशाओं में प्रत्येक तरंगाग्र की आकृति क्या है?
(a) किसी बिन्दु स्रोत से अपसरित प्रकाश
(b) उत्तल लेंस से निर्गमित प्रकाश, जिनमें फोकस बिन्दु पर कोई स्रोत रखा है।
(c) किसी दूरस्थ तारे से जाने वाले प्रकाश तरंगाग का पृथ्वी द्वारा अवरोधिक (Intercepted) भाग।
उत्तर:
(a) जब एक बिन्दु स्रोत से प्रकाश अपसरित होता है, तब तरंगान गोलीय अभिसारी प्रकार का होता है।
(b) जब बिन्दु स्रोत को उत्तल लेंस के फोकस पर रखा जाता है तब कलेंस से निर्गत प्रकाश किरणें एक - दूसरे के समान्तर होती हैं तथा तरंगाग्न समतल होता है।
(c) इस स्थिति में तरंगान की आकृति लगभग समतल होती है क्योंकि प्रकाश स्रोत पृथ्वी से दूरस्थ तारा है, अत: बड़े गोले के पृष्ठ पर छोटा क्षेत्रफल लगभग समतल है।

प्रश्न 3.
(a) कांच का अपवर्तनांक 1.5 है। काँच में प्रकाश की चाल क्या होगी? (निर्यात में प्रकाश की चाल 3.0 x 10⁸ m/s है)
(b) क्या कांच में प्रकाश की चाल, प्रकाश के रंग पर निर्भर करती है? यदि हाँ, तो लाल तथा बैंगनी में से कौन-सा रंग काँच के प्रिज्म में धीमा चलता? 
उत्तर:
(a) दिया है _aµ_g = 1.5
C = 3.0 x 10⁸ m/s 
काँच में प्रकाश की चाल Vg = ?
\(v_g=\frac{\mathrm{C}}{{ }_a \mu_g}=\frac{3 \times 10^8}{1.5}\)
v_g = 2 x 10⁸ ms^-1

(b) हाँ, काँच में प्रकाश की चाल उसके रंग पर निर्भर करती है। कोची सूत्र के अनुसार अपवर्तनांक रंग पर निर्भर है।
\(\mu=a+\frac{b}{\lambda^2}+\frac{b}{\lambda^4}+\ldots \ldots \ldots\)
अथवा \(\frac{C}{v}=a+\frac{b}{\lambda^2}+\ldots \ldots \ldots\)
यहाँ v काँच में प्रकाश की चाल है।
चूँकि 0, a तथा b नियत है। अत: v का मान तरंगदैर्ध्य λ पर निर्भर करता है। हम जानते हैं कि\( \lambda_V<\lambda_R \)अर्थात् बैंगनी रंग की तरंगदैर्ध्य लाल रंग की तरंगदैर्ध्य से कम है, इसलिए काँच में से बैंगनी प्रकाश लाल रंग की अपेक्षा धीमे चलेगा।

प्रश्न 4. 
यंग के द्विझिरी प्रयोग में झिरियों की बीच की दूरी 0.28 mm है तथा पदार्थ 1.4 m की दूरी पर रखा गया है। केन्द्रीय दीप्त फ्रिज एवं चतुर्थ दीप्त फ्रिन्ज के बीच की दूरी 1.2 cm मापी गई है। प्रयोग में उपयोग किए गए प्रकाश की तरंगदैर्ध्य ज्ञात कीजिए। 
उत्तर:
दिया है - d = 0.28 mm = 2.8 x 10^-4 m
D = 1.4 m
n = 4
y_n = 1.2 cm = 1.2 x 10^-2 m 
केन्द्रीय फ्रिज से वी फ्रिन्ज की दूरी

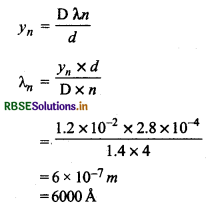
प्रश्न 5. 
बंग के द्विझिरी प्रयोग में λ तरंगदैयं का एकवर्णीय प्रकाश उपयोग करने पर, परदे के एक बिन्दु पर जहाँ पथान्तर λ है, प्रकाश की तीव्रता K इकाई है। उस बिन्दु पर प्रकाश की तीव्रता कितनी होगी जहाँ पथान्तर λ/3 है।
उत्तर:
दिया है- जब पथान्तर λ तथा I₁ = K 
जब पथान्तर \(=\frac{\lambda}{3}\) तथा I₂ = ?

अतः सूत्र \(\mathrm{I}=\dot{\mathrm{I}}_1+\mathrm{I}_2+2 \sqrt{\mathrm{I}, \mathrm{I}_2} \cos \theta\) से 
θ₁ कलान्तर के लिए
\(\begin{aligned} I^{\prime \prime} &=I+I \times 2 \sqrt{I \times I} \cos \frac{2 \pi}{3} \\ &=2 I+2 I\left(-\frac{1}{2}\right) \end{aligned}\)
अथवा I' = 4I = K (दिया है) ...................(1)
तथा θ₂ कलान्तर के लिए
\(\begin{aligned} I^{\prime \prime} &=I+I \times 2 \sqrt{I \times I} \cos \frac{2 \pi}{3} \\ &=2 I+2 I\left(-\frac{1}{2}\right) \end{aligned}\)
अथवा I'' = I
इसमें समीकरण (i) = \(\frac{\mathrm{K}}{4}\) रखने घर
I'' = \(\frac{\mathrm{K}}{4}\)

प्रश्न 6. 
यंग के द्विझिरी प्रयोग में व्यतिकरण फ्रिन्जों को प्राप्त करने के लिए 650 m तथा 520 mm तरंगदैयों के प्रकाश पुंज का उपयोग किया गया।
(a) 650 nm तरंगदैर्ध्य के लिए परदे पर तीसरे दीप्त फ्रिन्ज से केन्द्रीय बच्चिष्ठ की दूरी ज्ञात कीजिए।
(b) केन्द्रीय च्चिष्ठ से उस न्यूनतम दूरी को ज्ञात कीजिए जहाँ दोनों तरंगदैर्यों के कारण दीप्त फ्रिन्ज संपाती होते हैं।
उत्तर:
दिया है - स्लिटों के बीच की दूरी d = 2 x 10^-3 m
स्रोत से पर्दे की दूरी D = 1.20 m
λ₁ = 650 x 10^-9 m
λ₂ = 520 x 10^-9 m
(a) केन्द्रीय उच्चिष्ठ से n वौं फ्रिन्ज की दूरी
\(y_n=\frac{\mathrm{D} \lambda}{d} \times n\) से
\(y_3=\frac{1.20 \times 650 \times 10^{-9} \times 3}{2 \times 10^{-3}}\)
y_n = 1.17 x 10^-3 m

(b) माना λ₁, की n वीं फ्रिन्ज तथा λ₂ को (x + 1) वीं फ्रिन्ज संपाती है,
तब \(n \beta_1=(n+1) \beta_2\)

n = 4
∴ केन्द्रीय उच्चिष्ठ से दूरी
\(\begin{aligned} y &=n \beta_1=n \frac{\mathrm{D} \lambda_1}{d} \\ &=\frac{4 \times 1.20 \times 650 \times 10^{-9}}{2 \times 10^{-3}} \\ &=1.56 \times 10^{-3} \mathrm{~m} \end{aligned}\)

प्रश्न 7. 
एक द्विझिरी प्रयोग में एक मीटर दूर रखे परदे पर एक फ्रिज की कोणीय चौड़ाई 0.2° पाई गई। उपयोग किए गए प्रकाश की तरंगदैर्ध्य 600 nm है। यदि पूरा प्रायोगिक उपकरण जल में डुबो दिया जाए तो फ्रिन्ज की कोणीय चौड़ाई क्या होगी? जल का अपवर्तनांक 4/3 लीजिए। 
उत्तर:
दिया है- λ = 600 nm = 600 x 10^-9 m
θ = 0.2° 
D = 1 मीटर
पानी में फ्रिज की कोणीय चौड़ाई θ_w = ? 
फ्रिज की चौड़ाई के सूत्र \(\beta=\frac{\mathrm{D} \lambda}{d}\) से 
कोणीय चौड़ाई θ = \(\frac{\beta}{\mathrm{D}}=\frac{\lambda}{d}\)
वायु में \(\theta_a=\frac{\lambda_a}{d}\)
जल में \(\theta_w=\frac{\lambda_w}{d}\)
\(\frac{\theta_a}{\theta_w}=\frac{\lambda_a}{\lambda_w}=\mu\)
अथवा \(\theta_w=\frac{\theta_a}{\mu}=\frac{0.2}{4 / 3}=0.15\)

प्रश्न 8. 
वायु में संक्रमण के लिए बूस्टर कोण क्या है? (काँच का अपवर्तनांक = 1.5)
उत्तर:
दिया है- µ = 1.5, i_p = ? 
ब्रूस्टर के नियम से µ =  tan i_p
tan i_p = 1.5 
i_p = tan^-1 (1.5)
= 56.3° 

प्रश्न 9.
5000 Å तरंगदैर्ध्य का प्रकाश एक समतल परावर्तक पृष्ठ पर आपतित होता है। परावर्तित प्रकाश की तरंगदैर्ध्य तथा आवृत्ति क्या है? आपतन कोण के किस मान के लिए परावर्तित किरण आपतित किरण के लम्बवत होगी?
उत्तर:
परावर्तित प्रकाश की तरंगदैर्ध्य तथा आवृत्ति वही होगी जो आपतित प्रकाश की है। 
आवृत्ति \(v=\frac{\mathrm{C}}{\lambda}\)
C = 3 x 10⁸ मी/से 
λ = 5000 Å = 5 x 10^-7 मी.
∴ \(v=\frac{3 \times 10^8}{5 \times 10^{-7}}=6 \times 10^{14}\) हर्ट्ज
यहाँ XY परावर्तक समतल है। OA तथा AB आपतित एवं परावर्तित किरणें हैं।
i = आपतन कोण
r = परावर्तन कोण 
चूँकि AB तथा OA परस्पर लम्बवत हैं
i + r = 90°
परावर्तन के नियमानुसार
r = i
i + i = 90°
2i = 90°
i = \(\frac{90^{\circ}}{2}\) = 45°

प्रश्न 10. 
उस दूरी का आंकलन कीजिए जिसके लिए किसी 4 mm के आकार के द्वारक तथा 400 nm तरंगदैर्ध्य के प्रकाश के लिए किरण प्रकाशिकी सन्निकट रूप से लागू होती है।
उत्तर: 
दिया है- प्रकाश की तरंगदैर्ध्य λ = 400 nm = 400 x 10^-9 m 
छिद्र का द्वारक a = 4 x 10^-3 m
सूत्र \(\mathrm{Z}_f=\frac{a^2}{\lambda}\) से
\(\mathrm{Z}_f=\frac{\left(4 \times 10^{-3}\right)^2}{400 \times 10^{-9}}=40 \mathrm{~m}\)

प्रश्न 11. 
एक तारे में हाइड्रोजन से उत्सर्जित 6563 Å की Hλ लाइन में 15Å का अभिरक्त विस्थापन होता है। पृथ्वी से दूर जा रहे तारे की चाल का आंकलन कीजिये।
उत्तर:
दिया है: उत्सर्जित प्रकाश की तरंगदैर्ध्य λ = 6563 x 10^-10 मी.
डॉप्लर विस्थापन ∆λ = 15 x 10^-10 मीटर 
प्रकाश की चाल C = 38 x 10⁸ मीटर/सेकण्ड 
तारे की चाल v = ? 
सूत्र \(\Delta \lambda=\frac{v}{C} \times \lambda\) से
\(\begin{aligned} v &=\frac{C \times \Delta \lambda}{\lambda} \\ &=\frac{3 \times 10^8 \times 15 \times 10^{-10}}{6563 \times 10^{-10}} \end{aligned}\)
= 6.86 x 10⁵ मीटर/सेकण्ड 

प्रश्न 12. 
किसी माध्यम (जैसे जल) में प्रकाश की चाल निर्वात में प्रकाश की चाल से अधिक है। न्यूटन के कणिका सिद्धांत द्वारा इस आशय की भविष्यवाणी कैसे हो गई। क्या जल में प्रकाश की चाल प्रयोग द्वारा ज्ञात करके इस भविष्यवाणी की पुष्टि हुई? यदि नहीं, तो प्रकाश के चित्रण का कौन-सा विकल्प प्रयोगानुकूल है।
उत्तर:
न्यूटन के कणिका सिद्धांत के अनुसार प्रकाश कों के रूप में गमन करता है। जब प्रकाश विरल माध्यम से सघन माध्यम में प्रवेश करता है, तो प्रकाश कणों पर पृष्ठ के अभिलम्बवत एक आकर्षण बल कार्य करने लगता है, जिससे माध्यम के पृष्ठ पर वेग के लम्बवत घटक का मान बढ़ जाता है, लेकिन पृष्ठ के समान्तर घटक का मान अपरिवर्तित रहता है।
C sin i = v sin r
\(\frac{v}{\mathrm{C}}=\frac{\sin i}{\sin r}=\mu\)
जहाँ C वायु में प्रकाश की चाल है। \(i \text { व } r\) क्रमशः आपतन व अपवर्तन कोण है। वायु के सापेक्ष सघन माध्यम का अपवर्तनंक है।
∵ µ > 1
∴ v > C 
अर्थात् सघन माध्यम में प्रकाश का वेग विरल माध्यम में वेग की अपेक्षा अधिक होना चाहिए।
प्रयोगों द्वारा जल में प्रकाश की चाल ज्ञात करने पर अवधारणा की पुष्टि नहीं होती है। प्रायोगिक मापन में वायु की अपेक्षा जल में प्रकाश की चाल कम प्राप्त होती है। यह परिणाम प्रकाश के तरंग सिद्धांत के अनुकूल है।

प्रश्न 13. 
आप मूल पाठ में पढ़ चुके हैं कि हाइगेन्स का तरंग सिद्धान्त परावर्तन और अपवर्तन के नियमों के लिए किस प्रकार मार्गदर्शक है। इसी सिद्धान्त का उपयोग करके प्रत्यक्ष रीति से निगमन कीजिए कि समतल दर्पण के सामने रखी किसी वस्तु का प्रतिबिम्ब आभासी बनता है जिसकी दर्पण से दूरी उतनी ही होती है जितनी कि वस्तु की दर्पण से होती है।
उत्तर:
माना, एक समतल दर्पण XY के सामने एक बिन्दु बिम्ब O स्थित है। O से चलने वाला एक गोलीय तरंगाग्र APB समतल दर्पण के पृष्ठ पर चित्रानुसार आपतित है। OA, OP तथा OB रेखाएँ, जो तरंगान के बिन्दुओं A, P तथा B पर अभिलम्ब है, आपतित किरणे प्रदर्शित करती हैं। चूँकि दूरी OP दूरियों OA' तथा OB' से कम है, अत: O से चलने वाला विक्षोभ दर्पण के बिन्दुओं A' व B' पर पहुँचने के पूर्व ही बिन्दु P पर पहुँच जाता है। अत: जिस अण पर O से चलने वाला विक्षोभ A' व B' पर पहुँचता है, ठीक उसी क्षण पर P से चलने वाली द्वितीयक तरंगिकाएँ (OA' - OA) या (OB' - OB) त्रिज्या के गोलीय पृष्ठ के रूप में ले लेती है, तथा इस क्षण पर A' व B' भी द्वितीयक तरंगिकाओं के स्रोत बन जाते हैं जिनसे उत्पन्न द्वितीयक तरंगिकाओं की त्रिज्या शून्य होती है। परावर्तित तरंगाय (अर्थात समतल दर्पण से परावर्तन के पश्चात तरंगाग्न की नई स्थिति) प्राप्त करने के लिए, P को केन्द्र मानकर PP' = (OA' - OP) = (OB' - OP) त्रिज्या का एक गोला खींचा गया है। A'B' के बीच दर्पण के विभिन्न बिन्दुओं से चलने वाली द्वितीयक तरंगिकाओं का अन आवरण A'P' B' है जो परावर्तित तरंगान (जो अपसारी है) प्रदर्शित करता है। इस परावर्तित तरंगान के A',P; तथा B' बिन्दुओं पर IA', IP' के IB' अभिलम्ब हैं जो बिन्दु I पर मिलते हैं तथा परावर्तित किरणे प्रदर्शित करते हैं। स्पष्टतः परावर्तित तरंगाग्र बिन्दु I से आता हुआ प्रतीत होता है। अतः बिन्दुवत वस्तु 'O' का आभासी प्रतिबिम्ब I है

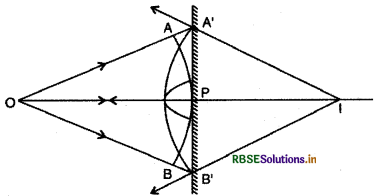
ज्यामिति से स्पष्ट है कि
PI = PO 
अर्थात् समतल दर्पण से प्रतिबिम्ब ठीक उतना ही पीछे बनता है जितना दर्पण के सामने वस्तु स्थित है।

प्रश्न 14. 
तरंग संचरण की चाल को प्रभावित कर सकने वाले कुछ संभावित कारकों की सूची है:
(i) स्रोत की प्रकृति
(ii) संचरण की दिशा
(iii) स्रोत और/या प्रेक्षक की गति
(iv) तरंगदैर्ध्य तथा
(v) तरंग की तीव्रता बताइए कि-
(a) निर्वात में प्रकाश की चाल
(b) किसी माध्यम (माना काँच या जल) में प्रकाश की चाल इनमें से किन कारकों पर निर्भर करती है?
उत्तर:
(a) निर्वात में प्रकाश की चाल एक सार्वत्रिक नियतांक है जो उपर्युक्त कारकों में से किसी पर भी निर्भर नहीं करती।

(b) माध्यम में प्रकाश की चाल की निर्भरता
(i) माध्यम में प्रकाश की चाल प्रकाश स्रोत की प्रकृति पर निर्भर नहीं करती।
(ii) किसी समरैखिक माध्यम में प्रकाश की चाल संचरण की दिशा पर निर्भर नहीं करती।
(iii) माध्यम में प्रकाश की चाल स्रोत और माध्यम की सापेक्ष गति से स्वतंत्र होती है लेकिन माध्यम के सापेक्ष प्रेक्षक की गति पर निर्भर करती है।
(iv) माध्यम में प्रकाश की चाल तरंगदैर्ध्य पर निर्भर करती है।
(v) किसी माध्यम में प्रकाश की चाल उसकी तीव्रता पर निर्भर नहीं करती।

प्रश्न 15.
ध्वनि तरंगों में आवृत्ति विस्थापन के लिए डॉप्लर का सूत्र निम्नलिखित दो स्थितियों में थोड़ा - सा भिन्न है: (i) स्रोत विरामावस्था में तथा प्रेक्षक गति में हो, तथा (ii) स्रोत गति में परन्तु प्रेक्षक विरामावस्था में हो। जबकि प्रकाश के लिए डॉप्लर के सूत्र निश्चित रूप से निर्वात, इन दोनों स्थितियों में एकसमान हैं। ऐसा क्यों है? स्पष्ट कीजिए। क्या आप समझते हैं कि ये सूत्र किसी माध्यम में प्रकाश गमन के लिए भी दोनों स्थितियों में पूर्णतः एक समान होंगे?
उत्तर:
ध्वनि तरंगों के लिए डॉप्लर का प्रभाव असममित होता है अर्थात् स्थिति (i) व (ii) में स्रोत तथा प्रेक्षक के बीच समान आपेक्षिक वेग के संगत आवृत्ति में होने वाला आभासी परिवर्तन समान नहीं है। इसका कारण है कि ध्वनि तरंगों के संचरण के लिए माध्यम की आवश्यकता होती है।
प्रकाश में डॉप्लर का प्रभाव सममित होता है अर्थात स्थिति (i) व (ii) में स्रोत तथा प्रेक्षक के बीच समान आपेक्षिक वेग के संगत आवृत्ति में होने वाला आभासी परिवर्तन समान है। निर्वात में प्रकाश तरंगों के लिए स्थितियों (i) व (ii) में कोई अंतर नहीं है। इसका कारण है कि स्रोत तथा प्रेक्षक के बीच सापेक्ष गति इस बात पर निर्भर नहीं करती है कि स्रोत गतिमान है अथवा प्रेक्षक। लेकिन किसी माध्यम में प्रकाश तरंगों के लिए भी स्थिति (i) व (ii) समान नहीं होगी। ध्वनि तरंगों की भांति ही प्रकाश तरंगों के लिए भी माध्यम की उपस्थिति में डॉप्लर प्रभाव असममित होगा।

प्रश्न 16.
द्विझिरी प्रयोग में 600 nm तरंगदैर्ध्य का प्रकाश करने पर, एक दूरस्थ परदे पर बने फ्रिज की कोणीय चौड़ाई 0.1° है। दोनों झिरियों की बीच कितनी दूरी है?
उत्तर:
दिया है- 
फ्रिज की कोणीय चौड़ाई θ = 0.1°
\(=0.1 \times \frac{\pi}{180}\) रेडियन 
प्रकाश की तरंगदैर्ध्य λ = 600 nm = 600 x 10^-9 मीटर 
झिरियों के बीच दूरी d = ? 
फ्रिज की कोणीय चौड़ाई के सूत्र \(\theta=\frac{\lambda}{d}\) से
\(\begin{aligned} d &=\frac{\lambda}{\theta}=\frac{600 \times 10^{-9}}{\left(0.1 \times \frac{\pi}{180^{\circ}}\right)} \\ &=\frac{6 \times 10^{-7} \times 180}{0.1 \times 3.14} \end{aligned}\)
= 3.44 x 10^-4 मीटर

प्रश्न 17. 
निम्नलिखित प्रश्नों के उत्तर दीजिए
(a) एकल झिरी विवर्तन प्रयोग में, झिरी की चौड़ाई मूल चौड़ाई से दोगुनी कर दी गई है। यह केन्द्रीय विवर्तन बैंड के आकार तथा तीव्रता को कैसे प्रभावित करेगी?
(b) द्वि - झिरी प्रयोग में प्रत्येक झिरी का विवर्तन, व्यतिकरण पैटर्न से किस प्रकार संबंधित है?
(c) सुदूर स्रोत से आने वाले प्रकाश के मार्ग में जब एक लघु वृत्ताकार वस्तु रखी जाती है, तो वस्तु की छाया के मध्य एक प्रदीप्त बिन्दु दिखाई देता है। स्पष्ट कीजिए, क्यों?
(d) दो विद्यार्थी एक 10 m ऊँची कक्ष विभाजक दीवार द्वारा 7 m के अन्तर पर हैं। यदि ध्वनि और प्रकाश दोनों प्रकार की तरंगें वस्तु के किनारों पर मुड़ सकती हैं तो फिर वे विद्यार्थी एक - दूसरे को देख क्यों नहीं पाते तथा वे आपस में आसानी से वार्तालाप किस प्रकार कर पाते हैं?
(e) किरण प्रकाशिकी, प्रकाश के सीधी रेखा में गति करने की संकल्पना पर आधारित है। विवर्तन प्रभाव (जब प्रकाश का संचरण एक द्वारक/झिरी या वस्तु के चारों ओर प्रेक्षित किया जाए) इस संकल्पना को नकारता है। तथापि किरण प्रकाशिकी की संकल्पना प्रकाशकीय यन्त्रों में प्रतिबिम्बों की स्थिति तथा उनके दूसरे अनेक गुणों को समझने के लिए सामान्यतः प्रयोग में लाई जाती है। इसका क्या औचित्य है?
उत्तर: 
(a) एकल झिरी विवर्तन प्रतिरूप में केन्द्रीय उच्चिष्ठ को चौड़ाई \(x=\frac{2 \mathrm{D} \lambda}{2}\)
जहाँ 'e' झिरी की चौड़ाई है, D पर्दे की झिरी से दूरी तथा λ प्रयुक्त प्रकाश की तरंगदैर्ध्य है।
झिरी की चौड़ाई (e) का मान दुगुना करने के केन्द्रीय उच्चिष्ठ की चौड़ाई अपने पूर्व मान की आधी रह जाएगी तथा इसकी तीव्रता बढ़कर चार गुनी हो जाएगी।
(b) द्वि - शिरी प्रयोग में व्यतिकरण फ्रिन्जों की तीव्रता प्रत्येक झिरी के विवर्तन प्रतिरूप द्वारा परिवर्धित होती है।
(c) लघु वृत्ताकार अवरोधक के किनारों से विवर्तित प्रकाश तरंगें छाया के केन्द्र पर सम्पोषी व्यतिकरण द्वारा प्रदीप्त बिन्दु उत्पन्न करती है।
(d) तरंगों के बड़े कोण पर विवर्तन के लिए अवरोधक या छिद्र का आकार तरंग की तरंगदैर्ध्य के समकक्ष होना चाहिए। यदि द्वारक या अवरोधक आकार तरंगदैर्य की तुलना में बहुत बड़ा हो, तो विवर्तन बहुत छोटे कोण से होगा। यहाँ अवरोधक का आकार कुछ मीटर कोटि का है। प्रकाश की तरंगदैर्ध्य लगभग 5 x 10^-7 मीटर होती है अतः दीवार से प्रकाश का विवर्तन नहीं होता है। विद्यार्थियों के वार्तालाप में ध्वनि तरंगों का तरंगदैर्ध्य लगभग 1 मीटर होती है।
अतः ये विभाजक दीवार के किनारों से मुड़ जाती है और विद्यार्थी सुगमता से वार्तालाप कर लेते हैं।
(e) प्रकाशिक यंत्रों में द्वारक का आकार प्रयुक्त प्रकाश की तरंगदैर्घ्य की तुलना में अत्यधिक बड़ा होता है, अत: प्रकाश तरंगों का विवर्तन उपेक्षणीय हो जाता है।

प्रश्न 18. 
दो पहाड़ियों की चोटी पर दो मीनारें एक - दूसरे से 40 km दूरी पर हैं। इनको जोड़ने वाली रेखा मध्य में आने वाली किसी पहाड़ी के 50 m ऊपर से होकर गुजरती हैं। उन रेडियो तरंगों की अधिकतम तरंगदैर्घ्य ज्ञात कीजिए, जो मीनारों के मध्य बिना पर्याप्त विवर्तन प्रभाव के भेजी जा सके।
उत्तर:
यदि बिना विवर्तन प्रभाव के अधिकतम तरंगदैर्ध्य λ_m हो तो 
फ्रेस्नेल दूरी \(\mathrm{Z}_{\mathrm{F}}=\frac{e^2}{\lambda}\)
यहाँ \(\mathrm{Z}_{\mathrm{F}}=\frac{40}{2}=20 \mathrm{~km}=2 \times 10^4\) मी.
e = 50 मीटर
\(\begin{aligned} \lambda_m &=\frac{e^2}{Z_{\mathrm{F}}} \\ &=\frac{(50)^2}{2 \times 10^4} \end{aligned}\)
= 12.5 x 10^-2 मी.
= 125 मिमी. 

प्रश्न 19.
500 nm तरंगदैर्ध्य का एक समान्तर किरण पुंज एक पतली झिरी पर आपतित होता है। इससे 1 मीटर दूर स्थित एक पर्दे पर परिणामी विवर्तन प्रतिरूप प्राप्त होता है। प्रथम निम्निष्ठ पर्दे के केन्द्र से 2.5 mm दूरी पर देखा जाता है। झिरी की चौड़ाई ज्ञात कीजिए।
उत्तर:
दिया है- झिरी से परदे की दूरी D = 1 मीटर 
प्रकाश की तरंगदैर्ध्य \(\lambda=500 \times 10^{-9}\) मीटर 
पर्दे के केन्द्र से प्रथम निम्निष्ठ की दूरी y = 25 mm = 2.5 x 10^-3 मी. 
झिरी की चौड़ाई \(y_1=\frac{\mathrm{D} \lambda}{e}\) से
\(\begin{aligned} e &=\frac{D \lambda}{y_1} \\ &=\frac{1 \times 500 \times 10^{-9}}{2.5 \times 10^{-3}} \end{aligned}\)
= 2.0 x 10^-4 मीटर
= 0.2 सेमी.

प्रश्न 20. 
निम्नलिखित प्रश्नों के उत्तर दीजिए
(a) जब कम ऊंचाई पर उड़ने वाला वायुयान ऊपर से गुजरता है, तो हम कभी - कभी टेलीविजन के पर्दे पर चित्र को हिलते हुए पाते हैं। इसका सम्भावित कारण बताइये।
(b) जैसा कि आप मूल पाठ में पढ़चुके हैं। विवर्तन तथा व्यतिकरण प्रतिरूप में तव्रिता का वितरण समझने के लिए आधारभूत सिद्धान्त तरंगों का रेखीय प्रत्यारोपण है। इस सिद्धांत की तर्क संगति क्या है?
उत्तर:
(a) कम ऊँचाई पर उड़ता वायुयान टेलीविजन संकेतों को परावर्तित करता है। सीधे आने वाले तथा परावर्तित टेलीविजन संकेतों के बीच व्यतिकरण होने के कारण पर्दे पर चित्र हिलता हुआ दिखाई देता है।
(b) अध्यारोपण का सिद्धांत तरंग गति को प्रदर्शित करने वाले अवकल समीकरण के रेखीय चरित्र से प्रतिपादित है।

प्रश्न 21. 
एकल झिरी विवर्तन प्रतिरूप की व्युत्पत्ति में यह कहा गया है। कि \(\frac{n \lambda}{e}\) कोणों पर तीव्रता शून्य होती है। इस निरसन को झिरी के उपयुक्त भागों में बांट कर सत्यापित कीजिए।
उत्तर:
माना, झिरी की चौड़ाई e है। इसे n समान चौड़ाई की झिरियों से बनी माना जा सकता है जिसमें प्रत्येक झिरी की चौड़ाई
e₁ = \(\frac{e}{n}\)
अब निम्निों की कोणीय स्थितियाँ
\(\theta=+\frac{n \lambda}{e}=\pm \frac{n \lambda}{n e_1}=+\frac{\lambda}{e_1}\)
अर्थात प्रत्येक छोटी झिरी से θ कोण पर तीव्रता शून्य है। अत: सभी छोटी झिरियों के कारण θ कोण पर तीव्रताओं का योग भी शून्य होगा।