RBSE Solutions for Class 12 Physics Chapter 10 Wave Optics

Rajasthan Board RBSE Solutions for Class 12 Physics Chapter 10 Wave Optics Textbook Exercise Questions and Answers.

RBSE Class 12 Physics Solutions Chapter 10 Wave Optics

RBSE Class 12 Physics Wave Optics Textbook Questions and Answers

Question 10.1.
Monochromatic light of wavelength 589 nm is incident from air on a water surface. What are the wavelength, frequency and speed of (a) reflected and (b) refracted light? Refractive index of water is 1.33.
Answer:
λ = 589 nm = 589 x 10^-9 m
(а) Reflected light: (Wavelength frequency, speed the same as incident light) = 589 nm, v = 5.09 x 10¹⁴ Hz, c = 3.00 x 10⁸ ms^-1.
v = \(\frac{c}{\lambda}=\frac{3 \times 10^8}{589 \times 10^{-9}}\)
= 5.093 x 10¹⁴ Hz

(b) Refracted light: (frequency the same as the incident frequency)
v = 5.093 x 10¹⁴ Hz.
v = \(\frac{c}{\mu}=\frac{3 \times 10^8}{1.33}\) = 2.256 x 10⁸ ms^-1
λ = \(\frac{v}{v}=\frac{2.26 \times 10^8}{5.09 \times 10^{14}}\) = 443 nm.

Question 10.2.
What is the shape of the wavefront in each of the following cases:
(a) Light diverging from a point source.
(b) Light emerges out of a convex lens when a point source is placed at its focus.
(c) The portion of the wavefront of light from a distant star intercepted by the earth.
Answer:
(a) It is spherical wavefront.
(b) It is plane wavefront.
(c) Plane wavefront (a small area on the surface of a large sphere is nearly planar.)

Question 10.3.
(a) The refractive index of glass is 1.5. What is the speed of light in glass? (Speed of light in vacuum is 3.0 x 10⁸ ms^-1).
(b) Is the speed of light in glass independent of the color of light? If not, which of the two colors red and violet, travels slower in a glass prism?
Answer:
(a) µ = \(\frac{c}{v}\)
or v = \(\frac{c}{µ} = \frac{3 \times 10^8}{1.5}\) = 2 x 10⁸ ms^-1.

(b) No. The refractive index, and hence the speed of light in a medium, depends on wavelength, [When no particular wavelength or color of light is specified, we may take the given refractive index to refer to yellow color]. Now we know violet color deviates more than red in glass i.e. µ_V > µ_R. Therefore the violet component of white light travels slower than the red component.

Question 10.4.
In Young’s double slit experiment, the slits are separated by 0.28 mm and the screen is placed 1.4 m away. The distance between the central bright fringe and the fourth bright fringe is measured to be 1.2 cm. Determine the wavelength of light used in the experiment.
Answer:
d = 0.28 mm = 0.28 x 10^-3 m
D = 1.4 m, ß = 1.2 x 10^-2 m
n = 4

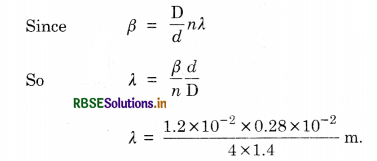
λ = 600 x 10^-9 m = 600 nm.

Question 10.5.
In Young’s double slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ and k units. What is the intensity of light at a point where path difference is \(\frac{\lambda}{3}\)?
Answer:
In Young’s double-slit experiment the intensity of light at any point is given as
Intensity = I₁ + I₂ + 2\(\sqrt{\mathrm{I}_1 \mathrm{I}_2}\) cos Φ .............(1)
Since phase difference
Φ = \(\frac{2 \pi}{\lambda} \cdot x\) (where x is path difference)
When path difference (x) = λ.
Phase difference (Φ) = \(\frac{2 \pi}{\lambda}\).λ = 2π.
So cos Φ = cos 2π = 1.
Put this in eq. (1), we get:
Intensity = I + I + 2\(\sqrt{\mathrm{I} . I}\)
∴ Intensity = 4I = k units
When x = λ/3
Φ = \(\frac{2 \pi}{\lambda} \times \frac{\lambda}{3}=\frac{2 \pi}{3}\)
∴ I' = I + I + 2\(\sqrt{\mathrm{I} . I}\) cos \(\frac{2 \pi}{3}=\frac{k}{4}\) units.

Question 10.6.
A beam of light consisting of two wavelengths 650 nm and 520 nm, is used to obtain interference fringes in Young’s double-slit experiment.
(a) Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
(b) What is the least distance from the central maximum where the bright fringes due to both wavelengths coincide? The distance between the slits is 2 mm and the distance between the plane of slits and the screen is 120 cm.
Answer:
Here λ₁ = 650 nm = 65 x 10^-8 m
λ₂ = 520 nm = 52 x 10^-8 m
d = 2 mm = 2 x 10^-3 m,
D = 120 cm = 1.2 m

(a) y₃ = \(\frac{3 \lambda \mathrm{D}}{d}=\frac{3 \times 65 \times 10^{-8} \times 1.2}{2 \times 10^{-3}}\)
= 1.17 x 10^-3 m = 1.17 mm

(b) Let n₁ the bright fringe of wavelength λ₁ coincides with n2th bright fringe of wavelength λ₂.
Then y' = \(\frac{n_1 \lambda_1 D}{d}=\frac{n_2 \lambda_2 D}{d}\)
or \(\frac{n_1}{n_2}=\frac{\lambda_2}{\lambda_1}=\frac{52 \times 10^{-8}}{65 \times 10^{-8}}=\frac{4}{5}\)
As n₁ and n₂ are integers, the minimum value of and n₂ satisfying the above equation are (4) and (5) respectively. The distance of 5th bright fringe for wavelength 52 x 10^-8 m (or 4th bright fringe for wavelength 65 x 10^-8 m)
∴ y' = \(\frac{n \lambda \mathrm{D}}{d}\)
or y' = \(\frac{4 \times 35 \times 10^{-8} \times 1.2}{2 \times 10^{-3}}\)
∴ y' = 15.6 x 10^-4 m = 1.56 mm.

Question 10.7.
In a double slit experiment, the angular width of a fringe is found to be 0.2° on a screen placed 1 m away. The wavelength of light used is 600 nm. What will be the angular width of the fringe If the entire experimental apparatus is immersed in water? Take refractive index of water to be 4/3.
Answer:
Here θ = 0.2°, λ = 600 nm = 6 x 10^-7 m,
µ = \(\frac{4}{3}\) =1.33.
In air
θ = \(\frac{\beta}{\mathrm{D}}=\frac{\frac{\lambda \mathrm{D}}{d}}{\mathrm{D}}=\frac{\lambda}{d}\)
In water
The wavelength of light
λ' = \(\frac{\lambda}{\mu}\)
∴ Angular width
θ' = \(\frac{\lambda^{\prime}}{d}=\frac{\lambda}{\mu d}=\frac{\theta}{\mu}=\frac{0.2^{\circ}}{1.33}\) = 0.15°.

Question 10.8.
What is the Brewster angle for air-to-glass transition? (refractive index of glass = 1.5).
Answer:
Given
µ = 1.5, θ = ?
Since µ = tan θ
∴ tan θ = 1.5
or θ = tan^-1 1.5 = 56.3°.

Question 10. 9.
Light of wavelength 5000 Å falls on a reflecting surface. What are the wavelength and frequency of the reflected light? For what angle of incidence is the reflected ray normal to the incident ray?
Answer:
Given λ = 5000 Å = 5 x 10^-7 m
The wavelength and frequency of reflected light remain the same.
∴ The wavelength of reflected light,
λ = 5000 Å
Frequency of reflected light,
v = \(\frac{c}{\lambda}=\frac{3 \times 10^8}{5 \times 10^{-7}}\) = 6 x 10¹⁴ Hz.
The reflected ray is normal to incident if angle of incidence i = 45°.

Question 10.10.
Estimate the distance for which ray optics is good approximation for an aperture of 4 mm and wavelength 400 mm.
Answer:
Given a = 4 mm = 4 x 10^-3 m.
λ = 400 nm = 4 x 10^-7 m
Z_F =?
∴ The minimum distance a beam of light has to travel before its deviation from straight line path becomes significant is called Fresnel distance Z_F 
∴ Z_F = \(\frac{a^2}{\lambda}=\frac{16 \times 10^{-6}}{4 \times 10^{-7}}\) = 40 m.

ADDITIONAL EXERCISES

Question 10.11.
The 6563 Å H_α line emitted by hydrogen in a star is found to be red-shifted by 15 Å. Estimate the speed with which the star is receding from the Earth.
Answer:
Given λ' - λ = 15 Å = 15 x 10^-10 m
λ = 6563 Å = 6563 x 10^-10 m
v = ?

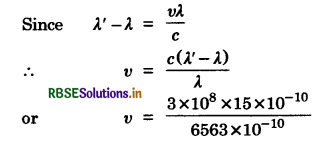
= 6.86 x 10⁵ ms^-1.

Question 10.12.
Explain how corpuscular theory predicts the speed of light in a medium, say water, is greater than the speed of light in vacuum. Is the prediction confirmed by experimental determination of the speed of light in water? If not, which alternative picture of light is consistent with experiment?
Answer:
In Newton’s corpuscular (Particle) picture of refraction, particles of light incident from a rarer to a denser medium experience a force of attraction normal to the surface. This results in an increase in the normal component of velocity but the component along the surface remains unchanged. This means
c sin i = v sin r
or \(\frac{v}{c}=\frac{\sin i}{\sin r}\) = µ.
Since µ > 1, ∴ v > c.
The prediction is opposite to the experimental result: (v < c). The wave picture of light is consistent with experiment.

Question 10.13.
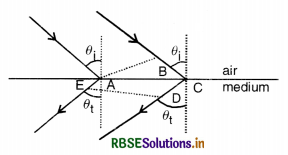
You have learned in the text how Huygens' principle leads to the laws of reflection and refraction. Use the same principle to deduce directly that a point object placed in front of a plane mirror produces a virtual image whose distance from the mirror is equal to the object's distance from the mirror.
Answer:
Image of a point object by reflection from a plane mirror.
Let O be a point object in front of plane mirror XY, at a normal distance OP from it. Fig. TBQ 10.13.

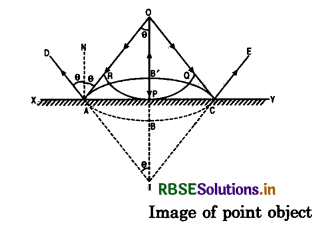
Spherical wavefront starts from it. A part RPQ of the wavefront touches the plane mirror at P. Whereas disturbance from R and Q continues moving forward along normals (rays) OR and OQ, that from P reflects back. When disturbances from R and Q reach the mirror at A and C respectively, that from P reaches B'. This gives rise to reflected spherical wavefront AB'C. ABC is the virtual position (position in absence of mirror) of the wavefront.
The reflected wavefront AB'C, appears to start from I. So I become virtual point image for O as real point object.
Draw AN, normal to XY, hence parallel to PO. Now OA is incident ray (being normal to incident wavefront ABC) and AD is reflected ray (being normal to reflected wavefront AB'C).
Hence ∠OAN = ∠DAN = θ (∵ i = r)
But ∠OAN = alternate ∠AOP
and ∠DAN = corresponding ∠AIP
∴ ∠AOP = ∠AIP
Now in As AIP and AOP,
∠    AIP = ∠AOP (each = θ)
∠API = ∠APO (each = 90°)
AP is common to both As become congruent
Hence PI = PO
i.e., normal distance of image from mirror = normal distance of object from mirror.
Thus virtual image is formed as much behind the mirror, as the object is in front of it.

Question 10.14.
Let us list some of the factors which could possibly influence the speed of wave propagation:    
(i) nature of the source
(ii) direction of propagation
(iii) motion of the source and /or observer
(iv) wavelength
(v) intensity of the wave.
On which of these factors, if any, does
(a) the speed of light in vacuum
(b) the speed of light in a medium (say glass or water) depend?
Answer:
(a) The speed of light in vacuum is a universal constant, independent of all the factors listed and anything else.

(b) Dependence of the speed of light in a medium:
(i) does not depend on the nature of the source (wave speed is determined by the properties of the medium of propagation. This is also true for other waves e.g. sound waves, water waves etc.)
(ii) independent of the direction of propagation for isotropic media.
(iii) Independent of the motion of the source relative to the medium but depends on the motion of the observer relative to the medium.
(iv) depends on wavelength.
(v) independent of intensity.

Question 10.15.
For sound waves, the Doppler formula for frequency shift differs slightly between the two situations: (i) source at rest: observer moving, and (ii) source moving: observer at rest. The exact Doppler formulae for the case of light waves in vacuum are, however, strictly identical for these situations. Explain why this should be so. Would you expect the formulae to be strictly identical for the two situations in case of light traveling in a medium?
Answer:
Sound waves require a medium for propagation. Thus even though situations (i) and (ii) may correspond to the same relative motion (between the source and the observer), they are. not identical physically Since the motion of the observer relative to the medium is different in the two situations. Therefore, we cannot expect, Doppler formulae for sound to be identical for (i) and (ii). For light waves in vacuum, there is clearly nothing to distinguish between (i) and (ii). Here only the relative motion between the source and the observer counts and the relativistic Doppler formula is the same for (i) and (ii). For light propagation in a medium, once again like sound waves, the two situations are not identical and we should expect the Doppler formulae for this case to be different for the two situations (i) and (ii).

Question 10.16.
In double slit experiment using light of wavelength 600 nm, the angular width of a fringe formed art a distant screen is 0.1°. What is the spacing between the two slits?
Answer:
Here λ = 600 nm = 6 x 10^-7 m,
θ = 0.1° = \(\frac{0.1^{\circ}}{180^{\circ}}\) x π rad
d = ?

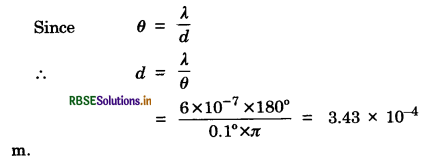
Question 10.17.
Answer the following questions:
(а) In a single-slit diffraction experiment, the width of the slit is made double the original width. How does this affect the size and intensity of the central diffraction band?
(b) In what way is diffraction from each slit related to the interference pattern in a double-slit experiment?
(c) When a tiny circular obstacle is placed in the path of light from a distant source, a bright spot is seen at the center of the shadow of the obstacle. Explain why?
(d) Two students are separated by a 7 m partition wall in a, room 10 m high. If both light and sound waves can bend around obstacles, how is it that the students are unable to see each other even though they can converse easily?
(e) Ray optics is based on the assumption that light travels in a straight line. Diffraction effects (observed when light propagates through small apertures/slits or around small obstacles) disprove this assumption. Yet the ray optics assumption is so commonly used in an understanding location and several other properties of images in optical instruments. What is the justification?
Answer:
(a) The size of central diffraction band reduces by half according to the relation: size λ/d. Intensity increases fourfold.

(b) The intensity of interference fringes in a double-slit arrangement is modulated by diffraction pattern of each slit.

(c) Waves diffracted from the edge of the circular obstacle interfere constructively at the center of the shadow producing a bright spot.

(d) For diffraction the size of the obstacle should be comparable to wavelength. If the size of the obstacle is much too large compared to wavelength, diffraction is by a small angle. Here the size partition of wall is of the order of a few meters. The wavelength of light is about 5 x 10^-7 m, while sound waves of say I kHz frequency have wavelengths of about 0.3 m. Thus sound waves can bend around the partition while light waves cannot.

(e) Typical sizes of apertures involved in ordinary optical instruments are much larger the wavelength.

Question 10.18.
Two towers on top of two hills are 40 km apart. The line joining them passes 50 m above a hill halfway between the towers. What is the longest wavelength of radio waves, which can be sent between the towers without appreciable diffraction effects?
Answer:
We want \(\frac{(5.0)^2}{\lambda} >> \frac{40,000}{2}\)
i.e. λ << \(\frac{(5.0)^2}{20,000}=\frac{250}{20,00}\)
= 0.125 m = 12.5 cm.

Question 10.19.
A parallel beam of light of wavelength 500 nm falls on a narrow slit and the resulting diffraction pattern is observed on a screen 1 m away. It is observed that the first minimum is at a distance of 2.5 mm from the center of the screen. Find the width of the slit.
Answer:
Here λ = 500 nm = 5 x 10^-7 m, D = 1 m, y = 2.5 mm = 2.5 x 10^-3 m, d = ?
For the first secondary minimum,
sin θ = \(\frac{\lambda}{d}=\frac{y}{\mathrm{D}}\)
∴ d = \(\frac{\lambda \mathrm{D}}{y}=\frac{5 \times 10^{-7} \times 1}{2.5 \times 10^{-3}}\) = 2 x 10^-4 m
= 0.2 mm.

Question 10.20.
Answer the following questions:
(a) When a low-flying aircraft passes over our heads, we sometimes note a slight shaking of the picture on our TV screen. Suggest a possible explanation.
(b) As you have learned in the text, the principle of linear superposition of wave displacement is basic to understanding intensity distributions in diffraction and interference patterns. What is the justification of the principle?
Answer:
(a) Interference of the direct signal received by the antenna with the (weak) signal reflected by the passing aircraft.
(b) Superposition principle follows from the linear character of the (differential) equation governing wave motion. It is true so long as waves have small amplitude.

Question 10.21.
In deriving the single slit diffraction pattern, it was stated that the intensity is zero at angles of nλ/a. Justify this by suitably dividing the slit to bring out the cancellation.
Answer:
Divide the single slit into n smaller slits of width a' = a/n. Each of the smaller slits sends zero intensity in the direction θ. The combination gives zero intensity as well.

SELECTED EXEMPLAR PROBLEMS

MCQ I [with one correct option]

Question 10. 1.
Consider a light beam incident from air to a glass slab at Brewster’s angle as shown in Fig. EP 10.1. A polaroid is placed in the path of the emergent ray at point P and rotated about an axis passing through the center and perpendicular to the plane of the polaroid. 
(a) For a particular orientation there shall be darkness as observed through the polaroid.
(b) The intensity of light as seen through the polaroid shall be independent of the rotation.
(c) The intensity of light as seen through the Polaroid shall go through a minimum but not zero for two orientations of the polaroid.
(d) The intensity of light as seen through the Polaroid shall go through a minimum for four orientations of the polaroid. 

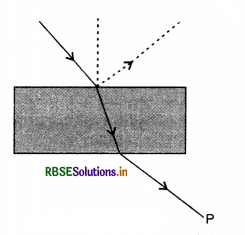
Answer:
(c) From Brewster’s law, we find that the emergent light is partially polarised so by rotating Polaroid, the intensity of light shall go through a minimum but not zero for two orientations of the Polaroid.

Question 10.2.
Consider sunlight incident on a slit of width 104 Å. The image seen through the slit shall
(a) be a fine sharp slit white in color at the center.
(b) a bright slit white at the center diffusing to zero intensities at the edges.
(c) a bright slit white at the center diffusing to regions of different colors.
(d) only be a diffused slit white in color.
Answer:
(a) Width of slit = 104 Å
Wavelength of white light is 4000 Å to 8000 Å so slit width >> wavelength of light, so no diffraction takes place and a fine sharp slit white in color at the center is seen.

Question 10.3.
Consider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at an angle θ. The phase difference between the ray reflected by the top surface of the glass and the bottom surface is:

Question 10.4.
In Young’s double-slit experiment, the source is white light. One of the holes is covered by a red filter and another by a blue filter. In this case.
(a) there shall be alternate interference patterns of red and blue.
(b) there shall be an interference pattern for red distinct from that for blue.
(c) there shall be no interference fringes.
(d) there shall be an interference pattern for red mixing with one for blue.
Answer:
(c) Since light will be of two colors (or wavelengths) and no interference will take place.

Question 10.5.
Figure EP 10.5 shows a standard two-slit arrangement with slits S₁, S₂, P₁, P₂ are the two minima points on either side of P.
At P₂ on the screen, there is a hole and behind P₂ is a second 2-slit arrangement with slits S₃, S₄ and a second screen behind them.

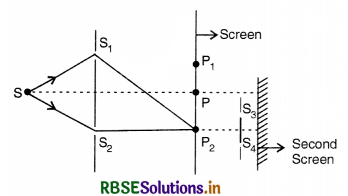
(a) There would be no interference pattern on the second screen but it would be lighted.
(b) The second screen would be totally dark.
(c) There would be a single bright point on the second screen.
(d) There would be a regular two slit pattern on the second screen.
Answer:
(d) Since there is a hole at P₂ (minima), the hole will act as a fresh light source for S₃ and S₄, so there would be a regular two-slit pattern on the second screen.

MCQ II. (with more than one correct options)

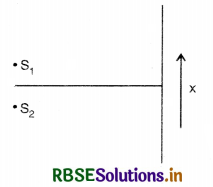
Question 10.6.
Two sources S₁ and S₂ of intensities I₁ and I₂ are placed in front of a screen [Fig. EP 10.6]. The pattern of intensity distribution seen in the central portion is given by Fig. 10.6.
In this case which of the following statements are true.
(a) S₁ and S₂ have the same intensities.
(b) S₁ and S₂ have a constant phase difference.

(c) S₁ and S₂ have the same phase.
(d) S₁ and S₂ have the same wavelength.
Answer:
(a), (b), (d)
Option (c) is incorrect

Question 10.7.
Consider sunlight incident on a pinhole of width 103 Å. The image of the pinhole seen on a screen shall be
(a) a sharp white ring.
(b) different from a geometrical image.
(c) a diffused central spot, white in color.
(d) diffused colored region around a sharp central white spot.
Answer:
(b), (d)
Wavelength of sunlight is 4000 Å to 8000 Å and width of pinhole is 103 Å = lOOO Å, so diffraction will take place, hence the image on the screen will he different from geometrical image and there will be diffused colored region around sharp central white spot.

Question 10.8.
Consider the diffraction pattern for a small pinhole. As the size of the hole is increased.
(a) the size decreases
(b) the intensity increases
(c) the size increases
(d) the intensity decreases.
Answer:
(a), (b)

Question 10.9.
For light diverging from a point source
(a) the wavefront is spherical.
(b) the intensity decreases in proportion to the distance squared.
(c) the wavefront is parabolic
(d) the intensity at the wavefront does not depend on the distance.
Answer:
(a), (b)
Light diverging from a point source is a diverging spherical wavefront
As intensity I ∝ \(\frac{\mathrm{P}}{4 \pi r^2}\) ⇒ I ∝ \(\frac{1}{r^2}\)
So intensity decreases in proportion to the distance squared.
 
Very Short Answer Type Questions

Question 10.10.
Is Huygens’ principle valid for longitudinal sound waves?
Answer:
Yes, it is valid for longitudinal sound waves.

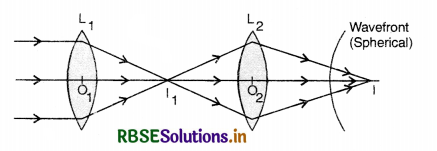
Question 10.11.
Consider a point at the focal point of a convergent lens. Another convergent lens of short focal length is placed on the other side. What is the nature of the wavefronts emerging from the final image?

Answer:
Considering the ray diagram we find that image I₁ due to L₁ is at focal point, we place another convergent lens L₂, the combination of L₁ and L₂ forms a real image, so the wavefront is spherical.

Question 10.12.
What is the shape of the wavefront on earth for sunlight?
Answer:
It will be spherical having very large radius as compared to radius of earth so it is almost a plane wavefront.

Question 10.13.
Why is the diffraction of sound waves more evident in daily experience than that of light waves?
Answer:
The condition for diffraction to take place is that the size of the obstacle or aperture should be comparable to wavelength of the wave to be diffracted.
Light has a wavelength 4 x 10^-7 m to 8 x 10^-7 m and obstacles or apertures of such size are generally not available, on the other hand, wavelength of sound is 15 m to 15 mm and obstacles or apertures of such size are generally available. Hence diffraction of sound waves is more evident in daily experience than that of light waves.

Question 10.14.
The human eye has an approximate angular resolution of Φ = 5.8 x 10^-4 rad and typical photo printer prints a minimum of 300 dpi (dots per inch, 1 inch = 2.54 cm). At what minimal distance z should a printed page be held so that one does not see the individual dots?
Answer:
Linear distance between two dots
l = \(\frac{2.54}{300}\)m =0.84 x 10^-2 cm
At a distance of z cm, this subtends an angle
Φ = \(\frac{l}{z}\)
or z = \(\frac{l}{\phi}=\frac{0.84 \times 10^{-2}}{5.8 \times 10^{-4}}\) = 14.5 cm

Question 10.15.
A polaroid (I) is placed in front of a monochromatic source. Another polaroid (II) is placed in front of this polaroid (I) and rotated till no light passes. A third polaroid (III) is now placed in between (I) and (II). In this case, will light emerge from (II). Explain.
Answer:
The given situation is as shown in Fig. 10.6

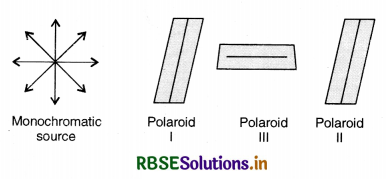
So when polaroid (III) is placed between I and II, light will not emerge from II, if pass axis of III is parallel to pass axis of I or II. In all other cases there shall be light emerging because the pass axis of II is no longer perpendicular to the pass axis of III.

Short Answer Type Questions

Question 10.16.
Can reflection result in plane polarised light if the light is incident on the interface from the side with higher refractive index?
Answer:
Yes. From Brewster’s law, we have
tan ip = n = \(\frac{n_2}{n_1}\), where n₂ < n₁
When light travels in such a medium, the critical angle C is given by
sin C = \(\frac{1}{n}=\frac{n_1}{n_2}\), where n₂ < n₁
As |tan ip| > |sin C| for large angles
∴ ip > C
Thus, polarization by reflection shall definitely occur.

Question 10.18.
Consider a two-slit interference arrangement (Fig. EP 10.18) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen fall at a distance D from the center O.

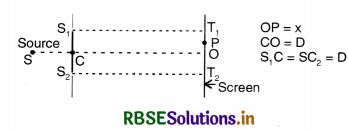
Answer:
From the given figure, we find that
T₂P = D + x, T₁P = D - x
Nowin rt ∠∆S₁T₁P and ∆S₂T₂P, we have
S₁P = \(\sqrt{\left(\mathrm{S}_1 \mathrm{~T}_1\right)^2+\left(\mathrm{PT}_1\right)^2}\)
= [D² + (D - x)²]^1/2
Similarly, S₂P = [D² + (D + x)²]^1/2
Minima will occur when

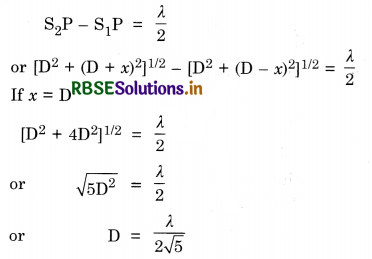
Long Answer Type Questions

Question 10.19.
Figure EP 10.19 shows a two-slit arrangement with a source that emits unpolarised light. P is a polariser with axis whose direction is not given. If I0 is the intensity of the principal maxima when no polariser is present, calculate in the present case, the intensity of the principal maxima as well as of the first minima.

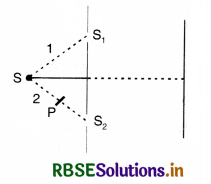
Answer:
Without P, resultant amplitude A is given by
A = A_⊥ + A_||
A_⊥ = A¹_⊥ + A²_⊥
= A⁰_⊥ sin (kx - ωt) + A⁰_⊥ sin (kx - ωt + Φ)
And A_|| = A¹_|| + A²_||
= A_||¹ [sin (kx - ωt) + sin (kx - ωt + Φ)]
where A⁰_⊥, A⁰₁₁ are the amplitudes of either of the beam in ⊥ and || polarisations.
∴ Intensity = |A⁰_⊥| + |A⁰₁₁|² [sin² (kx - ωt) (1 + cos² Φ + 2 sin Φ) + sin² (kx - ωt) sin² Φ)_average
= |A⁰_⊥| + |A⁰₁₁|²\left(\frac{1}{2}\right). 2 (1 + cos Φ)
= 2 |A_⊥⁰|² (1 + cos Φ) [∵ |A⁰_⊥|_average = |A⁰₁₁|]_average
With P
Assume A²_⊥ is blocked
∴ Intensity = (A¹_|| +A²_||)² + (A¹_⊥)²
= |A^0⊥|² (1 + cos Φ) + |A⁰_⊥|². \(\frac{1}{2}\)
Given I₀ = 4|A⁰_⊥|² = intensity without polariser at principal maxima
Intensity at principal maxima with polariser
= |A_0⊥|² \(\left[2+\frac{1}{2}\right]\) = \(\frac{5}{8}\) I₀
Intensity at first minima with polariser
= |A⁰_⊥|² (1 - 1) + \(\frac{\left|\mathrm{A}_{\perp}^0\right|^2}{2}=\frac{\mathrm{I}_0}{8}\)

Question 10.22.
The optical properties of a medium are governed by the relative permittivity (ε_r) and relative permeability (µ_r). The refractive index is defined as \(\sqrt{\mu_{\mathrm{r}} \varepsilon_{\mathrm{r}}}\) = n. For ordinary material ε_r > 0 and µ_r > 0 and the positive sign is taken for the square root. In 1964, Russian scientist V. Veselago postulated the existence of material with εr < 0 and µr < 0. Since then such ‘metamaterials’ have been produced in laboratories and their optical properties studied. For such materials n = -\(\sqrt{\mu_{\mathrm{r}} \varepsilon_{\mathrm{r}}}\). As light enters a medium of such refractive index the phases travel away from the direction of propagation.
(i) According to the description above shows that if rays of light enter such a medium from air (refractive index = 1) at an angle θ in the 2nd quadrant, then the refracted beam is in the 3rd quadrant.
(ii) Prove that Snell’s law holds for such a medium.
Answer:
(i) Suppose the postulate is true, then two parallel rays would proceed as shown in Fig. EP 10.22
(a) Assuming ED shows a wavefront then all points on this must have the same phase. All points with the same optical path length must have the same phase.
Thus = \(\sqrt{\varepsilon_r \mu_r}\) AE = BC - \(\sqrt{\varepsilon_r \mu_r}\) CD
or BC = \(\sqrt{\varepsilon_r \mu_r}\) (CD - AE)
As BC > 0, CD > AE

As showing that the postulate is reasonable. If however, the light proceeded in the sense it does for ordinary material (viz. in the fourth quadrant,
Fig. EP 10.22 (b)        
Then - \(\sqrt{\varepsilon_r \mu_r} \)AE = BC - \(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\sqrt{\varepsilon_r \mu_r}\) CD
or BC = \(\sqrt{\varepsilon_r \mu_r}\) (CD - AE)
As AE > CD, BC < 0

showing that this is not possible. Hence the postulate is correct.
(ii)From Fig. EP 10.22 (a)
BC - AC sin θ₁ and CD - AE = AC sin θ_r.
Since - \(\sqrt{\varepsilon_r \mu_r}\) (AE - CD) = BC
-n sin θ_r = sin θ_t.

Question 10.23.
To ensure almost 100 percent transmissivity, photographic lenses are often coated with a thin layer of dielectric material. The refractive index of this material is intermediated between that of air and glass (which makes the optical element of the lens). A typically used dielectric film is MgF₂ (n = 1.38). What should the thickness of the film be so that at the center of the visible spectrum (5500 Å) there is maximum transmission?
Answer:
Consider a ray incident at an angle i. A part of this ray is reflected from the air-film interface and a part refracted inside. This is partly reflected at the film-glass interface and a part transmitted. A part of the reflected ray is reflected at the film-air interface and a part is transmitted as r₂ parallel to r₁. Of course, successive reflections and transmissions will keep on decreasing the amplitude of the wave. Hence rays r₁ and r₂ shall dominate the behavior. If incident light is to be transmitted through the lens r₁ and r₂ should interfere destructively. Both the reflections at A and D are from lower to higher refractive index and hence there is no phase change on reflection. The optical path difference between r₂ and r₁ is
n (AD + CD) - AB.
If d is the thickness of the film, then
AD = CD = \(\frac{d}{\cos r}\)
AB = AC sin i
\(\frac{\mathrm{AC}}{2}\) = d tan r
∴ AC = 2d tan r
Hence, AB = 2d tan r sin i
Thus the optical path difference is
2n\(\frac{d}{\cos r}\) - 2d tan r sin i
= 2. \(\frac{\sin i}{\sin r} \frac{d}{\cos r}\) - 2d\(\frac{\sin r}{\cos r}\) sin i
= 2d sin\(\left[\frac{1-\sin ^2 r}{\sin r \cos r}\right]\)
= 2nd cos r

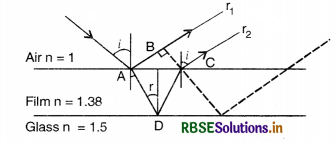
For these waves to interfere destructively this must be \(\frac{\lambda}{2}\)
⇒ 2nd cos r = \(\frac{\lambda}{2}\)
or nd cos r = \(\frac{\lambda}{4}\)
For a camera lens, the sources are in the vertical plane and hence i = r ≃ 0
∴ nd ≃ \(\frac{\lambda}{4}\)
or d = \(\frac{5500 \AA}{1.38 \times 4}\) = 1000Å