RBSE Solutions for Class 12 Physics Chapter 1 वैद्युत आवेश तथा क्षेत्र

Rajasthan Board RBSE Solutions for Class 12 Physics Chapter 1 वैद्युत आवेश तथा क्षेत्र Textbook Exercise Questions and Answers.

RBSE Class 12 Physics Solutions Chapter 1 वैद्युत आवेश तथा क्षेत्र

RBSE Class 12 Physics वैद्युत आवेश तथा क्षेत्र Textbook Questions and Answers

प्रश्न 1. 
वायु में एक - दूसरे से 30 cm की दूरी पर रखे दो छोटे आवेशित गोलों पर क्रमशः 2 x 10^-7C तथा 3 x 10^-7C आवेश हैं। उनके बीच कितना बल है?  
हल: 
गोलों पर दिया गया आवेश क्रमश:
q₁ = 2 x 10^-7C, q₂ = 3 x 10^-7C
दूरी r = 30 cm  =0.30m
F = ?
कूलॉम के नियम से गोलों के मध्य वैद्युत बल
F = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2}\)
= 9 x 10⁹ x \(\frac{2 \times 10^{-7} \times 3 \times 10^{-7}}{0.3 \times 0.3}\)
= 6 x 10^-3 N(प्रतिकर्षां) 

प्रश्न 2. 
0.4µC के आवेश के किसी छोटे गोले पर अन्य छोटे आवेशित गोले के कारण वायु में 0.2 N बल लगता है। यदि दूसरे गोले पर 0.8µC आवेश हो तो 
(a) दोनों गोलों के बीच कितनी दूरी है? 
(b) दूसरे गोले पर पहले गोले के कारण कितना बल लगता है? 
हल: 
(a) गोलों पर दिया गया आवेश
q₁ = 0.4µC = 0.4 x 10^-6 C
q₂ = 0.8µC = 0.8 x 10^-6C
∵ F₁₂ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2}\) या r₂ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{\mathrm{~F}_{12}}\)
या r² = 9 x 10⁹ x \(\frac{0.4 \times 10^{-6} \times 0.8 \times 10^{-6}}{0.2}\)
या r² = 9 x 4 x 4 x 10^-4
∴ r = 3 x 4 x 10^-2m
= 12 x 10^-2m 
= 12cm

(b) दो आवेशों के मध्य वैद्युत बल परिमाण में समान होते हैं अतः दूसरे गोले द्वारा पहले गोले पर बल
= पहले गोले द्वारा दूसरे पर बल 
|\(\overrightarrow{\mathrm{F}_{12}}\)| = |\(\overrightarrow{\mathrm{F}_{21}}\)|
∴ F₂₁ = F₁₂ = 0.2 N (आकर्षण) 

प्रश्न 3. 
जाँच द्वारा सुनिश्चित कीजिए कि \(\frac{k e^2}{\mathbf{G} m_e \cdot m_p}\) विमाहीन है। भौतिक नियतांकों की सारणी देखकर इस अनुपात का मान ज्ञात कीजिए। यह अनुपात क्या बताता है?
हल: 
कूलॉम बल 

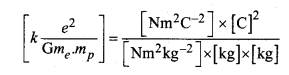
= कोई इकाई नहीं 
∵ अनुपात की कोई इकाई नहीं है अतः यह विमाहीन राशि है।
∵ k = 9x 10⁹ Nm²C^-2, 
e = 1.6 x 10^-19 C,
m_p = 1.66 x 10^-27kg,
m_e = 9.1 x 10^-31kg,
G = 6.67 x 10^-11 Nm²kg^-2
∴\( \frac{k e^2}{\mathrm{G} m_e m_p}=\frac{9 \times 10^9 \times\left(1.6 \times 10^{-19}\right)^2}{6 \cdot 67 \times 10^{-11} \times 9.1 \times 10^{-31} \times 1.66 \times 10^{-27}}\)
= 2.29 x 10³⁹

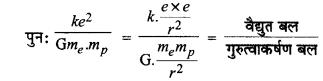
अतः यह राशि \(\left(\frac{k e^2}{\mathrm{G} m_e \cdot m_p}\right)\) एक इलेक्ट्रॉन एवं प्रोटॉन के बीच स्थिर वैद्युत बल तथा गुरुत्वाकर्षण बल के अनुपात को प्रदर्शित करती है। साथ ही साथ यह अनुपात (2.29x 10³⁹) यह बताता है कि इलेक्ट्रॉन एवं प्रोटॉन के मध्य विद्युत - स्थैतिक बल गुरुत्वाकर्षण बल की तुलना में काफी प्रबल है।

प्रश्न 4. 
(a) "किसी वस्तु का विद्युत् आवेश क्वाण्टीकृत है।" इस कथन से क्या तात्पर्य है?
(b) स्थूल अथवा बड़े पैमाने पर विद्युत् आवेशों से व्यवहार करते समय हम विद्युत् आवेश के क्वाण्टमीकरण की उपेक्षा कैसे कर सकते है?
उत्तर:
(a) किसी वस्तु के आवेश के क्वाण्टीकृत का अर्थ यह है कि हम किसी वस्तु को जितना चाहें उतना आवेश नहीं दे सकते अपितु आवेश की न्यूनतम इकाई, जिसे मूल आवेश कहते हैं जिसका मान e = 1.6  x  10^-19C होता है, के पूर्ण गुणों में ही दिया जा सकता है। अत: किसी वस्तु पर आवेश 
q =  \(\pm\)ne , जहाँ n = 1, 2, 3, 4, ... (पूर्ण संख्या) 

(b) स्थूल अथवा बड़े पैमाने पर आवेशों से व्यवहार करते समय आवेश के क्वाण्टमीकरण का कोई महत्त्व नहीं होता और इसकी उपेक्षा की जा सकती है। इसका कारण यह है कि बड़े पैमाने पर व्यवहार में आने वाले आवेश मूल आवेश की तुलना में बहुत बड़े होते हैं। उदाहरण के लिए, 1µC आवेश में लगभग 10¹³ मूल आवेश (e) सम्मिलित है। ऐसी अवस्था में आवेश को सतत मानकर व्यवहार किया जा सकता है।

प्रश्न 5. 
जब काँच की छड़ को रेशम के टुकड़े से रगड़ते हैं तो दोनों पर आवेश आ जाता है। इसी प्रकार की परिघटना का वस्तुओं के अन्य युग्मों में भी प्रेक्षण किया जाता है। स्पष्ट कीजिए कि यह प्रेक्षण आवेश संरक्षण के नियम से किस प्रकार सामंजस्य रखता है?
उत्तर:
घर्षण द्वारा आवेशन की घटनाएँ आवेश संरक्षण के साथ पूर्ण सामंजस्य रखती हैं। जब दो उदासीन वस्तुओं को रगड़ा जाता है तो एक वस्तु से कुछ इलेक्ट्रॉन दूसरी वस्तु पर चले जाते हैं जिससे दोनों वस्तुएँ आवेशित हो जाती है। एक वस्तु पर जितना ऋण आवेश आ जाता है, दूसरी पर उतना ही धनावेश आ जाता है। इस प्रकार यदि दोनों के आवेश को जोड़ दें तो उनका योग शुन्य मिलेगा। स्पष्ट है कि आवेशन से पूर्व और आवेशन के बाद कुल आवेश शून्य ही रहता है। यही आवेश संरक्षण का नियम है।

प्रश्न 6. 
चार बिन्दु आवेश q_A =2µC, q_B = -5µC, q_C = +2µC तथा q_D = -5µC, 10 cm भुजा के किसी वर्ग ABCD के शीर्षों पर अवस्थित हैं। वर्ग के केन्द्र पर रखे +1µC आवेश पर लगने वाला बल कितना है?

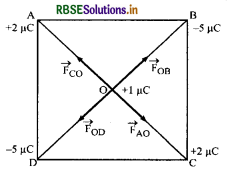
हल: 
वर्ग के शीर्षों A व C पर समान आवेश (+2µC) है अत: वर्ग के केन्द्र O पर रख्खे आवेश + 1µC पर परिमाण में समान किन्तु दिशा में विपरीत बल \(\overrightarrow{\mathrm{F}_{\mathrm{AO}}} \text { व } \overrightarrow{\mathrm{F}_{\mathrm{CO}}} \)लगेगा अर्थात्
\(\overrightarrow{\mathrm{F}_{\mathrm{AO}}}+\overrightarrow{\mathrm{F}_{\mathrm{CO}}}=0\)
इसी प्रकार शेष दो शीर्षों B व D पर समान आवेश -5µC रखे हैं अतः ये आवेश भी केन्द्र O पर रखे +1µC आवेश पर परिमाण में समान 
किन्तु दिशा में विपरीत बल \(\overrightarrow{\mathrm{F}_{\mathrm{OB}}} \text { व } \overrightarrow{\mathrm{F}_{\mathrm{OD}}}\) लगायेंगे अत: 
\(\overrightarrow{\mathrm{F}_{\mathrm{OB}}}+\overrightarrow{\mathrm{F}_{\mathrm{OD}}}=0\)
फलस्वरूप केन्द्र O पर रखे आवेश पर परिणामी बल

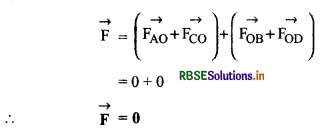
प्रश्न 7.
(a) स्थिर वैद्युत क्षेत्ररेखाएक सतत वक्र होती है, अर्थात् कोई क्षेत्र रेखा एकाएक नहीं टूट सकती, क्यों?
(b) स्पष्ट कीजिए कि दो क्षेत्र रेखाएँ कभी भी एक-दूसरे का प्रतिच्छेदन नहीं कर सकतीं, क्यों?
उत्तर:
(a) विद्युत क्षेत्र रेखा वह काल्पनिक वक्र है जिस पर स्वतन्त्रतापूर्वक छोड़ा गया धन परीक्षण आवेश चलता है और इसके किसी बिन्दु पर खींची गई स्पर्श रेखा उस बिन्दु पर परिणामी विद्युत् क्षेत्र की दिशा व्यक्त करती है। ये क्षेत्र रेखाएँ सतत बक्र होती हैं अर्थात् किसी बिन्दु पर एकाएक टूट नहीं सकती है अन्यथा उस बिन्दु पर विद्युत् क्षेत्र की कोई दिशा ही नहीं होगी, जो कि सम्भव नहीं है।

(b) वैद्युत क्षेत्र रेखाएँ (Electric Lines of Field)
"वैद्युत क्षेत्र में स्वतन्त्रतापूर्वक (freely) छोड़ा गया धन परीक्षण आवेश जिस मार्ग का अनुसरण (follow) करता है, उसे उस क्षेत्र की वैद्युत क्षेत्र - रेखा या विद्युत बल रेखा कहते हैं।" वैद्युत क्षेत्र रेखाओं की निम्नलिखित विशेषताएँ (characteristics) होती हैं-
(i) वैद्युत क्षेत्र रेखा के किसी बिन्दु पर खींची गई स्पर्श रेखा उस बिन्दु पर परिणामी विद्युत् क्षेत्र की दिशा व्यक्त करती है।
(ii) वैद्युत क्षेत्र रेखाएँ धन आवेश से ऋण आवेश की ओर चलती है।
(iii) दो क्षेत्र रेखाएँ कभी एक - दूसरे को नहीं काटती (intersect) हैं क्योंकि यदि वे काटेंगी तो कटान बिन्दु (point of intersection) पर दोनों वक्रों पर खींची गई स्पर्श रेखाएँ दो परिणामी विद्युत् क्षेत्र व्यक्त करेंगी जो कि सम्भव नहीं है। अत: क्षेत्र रेखाओं का काटना भी सम्भव नहीं है।

(iv) वैद्युत क्षेत्र रेखाएँ खुले वक्र (open curves) के रूप में होती हैं क्योंकि ये धनावेश से चलकर ऋणावेश पर समाप्त हो जाती हैं।
(v) वैद्युत क्षेत्र रेखाएँ किसी पृष्ठ से लम्बवत् बाहर निकलती है और पृष्ठ पर लम्बवत क्षेत्र ही समाप्त होती है।
(vi) किसी स्थान पर वैद्युत बल रेखाओं का पृष्ठ घनत्व (surface density) (एकांक क्षेत्रफल से गुजरने वाली क्षेत्र रेखाओं की संख्या) उस स्थान पर 'वैद्युत' क्षेत्र की तीव्रता के अनुपात में होता है अर्थात् क्षेत्र रेखाएँ जितनी सघन (dense) होंगी, वहाँ विद्युत् क्षेत्र उतना ही प्रबल (strong) होगा। क्षेत्र रेखाओं की संख्या के पदों में विद्युत् क्षेत्र की तीव्रता की परिभाषा निम्न प्रकार की जा सकती है-
"किसी स्थान पर क्षेत्र रेखाओं की दिशा के लम्बवत् एकांक क्षेत्रफल (unit area) से गुजरने वाली क्षेत्र रेखाओं की संख्या, उस स्थान पर विद्युत् क्षेत्र की तीव्रता के तुल्य होती है।"

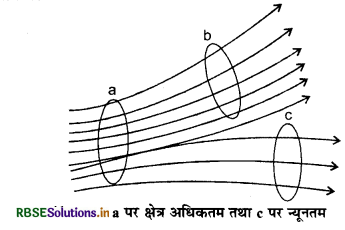
(vii) ये खिची हुई लचकदार डोरी (flexible string) की तरह लम्बाई में सिकुड़ने (contract) का प्रयत्न करती हैं। इसी कारण विपरीत आवेशों में आकर्षण होता है।
(viii) ये अपनी लम्बाई की लम्ब दिशा में एक-दूसरे से दूर रहने (for apart) का प्रयास करती हैं। इसलिए समान आवेशों के मध्य प्रतिकर्षण होता है।

प्रश्न 8. 
दो बिन्दु आवेश q_A = 3µC तथा q_B = -3µC निर्वात् में एक - दूसरे से 20 cm दूरी पर स्थित हैं।
(a) दोनों आवेशों को मिलाने वाली रेखा AB के मध्य - बिन्दु O पर विद्युत् क्षेत्र कितना है?
(b) यदि 1.5 x 10^-9 C परिमाण का कोई ऋणात्मक परीक्षण आवेश इस बिन्दु पर रखा जाए तो यह परीक्षण आवेश कितने बल का अनुभव करेगा?
उत्तर:
(a) बिन्दु O पर A के कारण विद्युत् क्षेत्र तथा B के कारण O पर विद्युत् क्षेत्र की दिशा एक ही है क्योंकि विद्युत् क्षेत्र धनात्मक आवेश से दूर तथा ऋणात्मक आवेश की ओर जाता है।

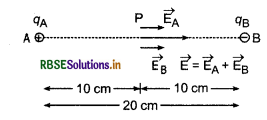
A के कारण बिन्दु O पर विद्युत् क्षेत्र, 
E_A = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_{\mathrm{A}}}{r^2}=\frac{9 \times 10^9 \times 3 \times 10^{-6}}{(0.10)^2}\)
= 27 x 10⁵ N/C OB की ओर
B के कारण O पर विद्युत क्षेत्र
E_B = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_{\mathrm{B}}}{r^2}=\frac{9 \times 10^9 \times 3 \times 10^{-6}}{(0.10)^2}\)
= 27 x 10⁵ N/C OB की ओर
E_O = E_A + E_R
= 27 x 10⁵ + 27 x 10⁵ 
= 54 x 10⁵ N/C,OB की दिशा में
=5.4 x 10⁶ N/C, OB की दिशा में 

(b) ऋणात्मक आवेश q = 1.5 x 10^-9C पर लगने वाला बल
F = qE_o
= -1.5 x 10^-9 x 5.4 x 10⁶ 
= -8.10 x 10^-3N
= - 8.1 x 10^-3N, OA की दिशा में 
ऋणात्मक चिह्न प्रदर्शित करता है कि वैद्युत बल की दिशा वैद्युत क्षेत्र की दिशा के विपरीत दिशा में है।

प्रश्न 9. 
किसी निकाय में दो आवेश q_A = 2.5 x 10^-7C तथा q_B = -2.5 x 10^-7C क्रमश: दो बिन्दुओं A : (0, 0,-15 cm) तथा B : (0, 0, + 15 cm) पर स्थित हैं। निकाय का कुल आवेश तथा विद्युत् द्वियुव आघूर्ण क्या है?

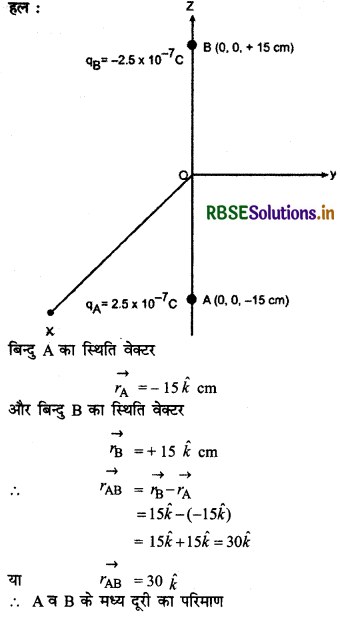
r_AB = \(\left|\overrightarrow{r_{\mathrm{AB}}}\right| = \sqrt{(30)^2}\) = 30 cm
या r_AB = 0.30 m
अतः वैद्युत द्विध्रुव की प्रभावी लम्बाई
2l = r_AB = 0.30 m
अत: विद्युत द्विध्रुव आघूर्ण
p = q.2l
= 2.5 x 10^-7 x 0.30
= 0.75 x 10^-7 = 7.5 x 10^-8 Cm

प्रश्न 10.
4 x 10^-9Cm द्विध्रुव आघूर्ण का कोई वैद्युत द्विधुव 5 x 10⁴ NC^-1 परिमाण के किसी एक - समान विद्युत् क्षेत्र की दिशा से 30° पर सरैखित है। द्विघुव पर कार्यरत बल आघूर्ण का परिमाण परिकलित कीजिए। 
हल:
दिया है: द्विध्रुव आघूर्ण
p = 4x10^-9 Cm 
विद्युत क्षेत्र की तीव्रता E = 5 x 10⁴ N/C 
विद्युत क्षेत्र के साथ द्विवव का कोण
θ = 30° 
द्विध्रुव पर आघूर्ण τ = ?
∴ τ = pE sinθ
= 4 x 10^-9 x 5 x 10⁴ x sin 30°
= 4 x 10^-9 x 5 x 10⁴ x \(\frac{1}{2}\)
= 10 x 10^-5 = 10^-4 Nm 

प्रश्न 11. 
ऊन से रगड़े जाने पर कोई पॉलीथीन का टुकड़ा 3 x 10^-7C के ऋणावेश से आवेशित पाया गया।
(a) स्थानान्तरित (किस पदार्थ से किस पदार्थ में) इलेक्ट्रॉनों की संख्या का आकलन कीजिए।
(b) क्या ऊन से पॉलीथीन में संहति (दव्यमान) का स्थानान्तरण भी होता है? 
हल: 
(a) टुकड़े पर आवेश
q = 3 x 10^-7C
पॉलीथीन का टुकड़ा ऋणावेशित होता है अतः इस पर इलेक्ट्रॉनों की अधिकता होगी और यह अधिकता यदि n है तो
q = ne, से n = \(\frac{q}{e}=\frac{3 \times 10^{-7}}{1.6 \times 10^{-19}}\) = 1.875 x 10¹²
अत: 1.875 x 10¹² इलेक्ट्रॉन ऊन से पॉलीथीन पर स्थानान्तरित होंगे।

(b) हाँ, द्रव्यमान का भी स्थानान्तरण होता है क्योंकि इलेक्ट्रॉन एक द्रव्यमान कण है अतः ऊन से पॉलीथीन पर द्रव्यमान स्थानान्तरित होगा। 
∴ स्थानान्तरित द्रव्यमान 
∆m = n.me = 1.875 x 10¹² x 9.1 x 10^-31 kg
= 1.7 x 10^-18 kg 

प्रश्न 12. 
(a) दो विद्युत्रोधी आवेशित ताँबे के गोलों तथा B के केन्द्रों के बीच की दूरी 50 cm है। यदि दोनों गोलों पर पृथक् - पृथक आवेश 6.5x10-7C हैं तो इनमें पारस्परिक स्थिर विद्युत् प्रतिकर्षण बल कितना है? गोलों के बीच की दूरी की तुलना में गोलों A तथा B की त्रिज्याएँ नगण्य हैं।
(b) यदि प्रत्येक गोले पर आवेश की मात्रा दोगुनी तथा गोलों के बीच की दूरी आधी कर दी जाये तो प्रत्येक गोले पर कितना बल लगेगा? (राजस्थान बोर्ड नमूना प्रश्न पत्र) 
हल: 
(a) गोलों A तथा B पर आवेश
q₁ = q₂ = + 6.5 x 10^-7C
दोनों के मध्य दूरी r = 50 cm = 0.5 m
∵ गोलों की त्रिज्याएँ उनके बीच की दूरी की तुलना में नगण्य हैं अत: उन्हें बिन्दु आवेश की तरह मान सकते हैं।
∴ दोनों गोलों के मध्य प्रतिकर्षण बल

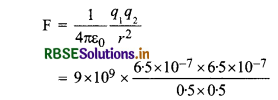
या F = 1.521 x 10^-2 N 

(b) जब आवेश की मात्रा दोगुनी एवं उनके बीच की दूरी आधी कर दी जाती है तो q₁' = 2q₁, q₂' = 2q₂
और r' = \(\frac{r}{2}\)
अतः अब गोलों के मध्य बल

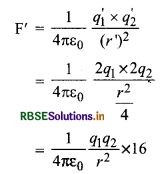
या F' = 16 F = 16 x 1.521 x 10^-2 = 0.24N 

प्रश्न 13. 
मान लीजिए प्रश्न 12 में गोले A तथा B साइज में सर्वसम हैं तथा इसी साइज का कोई तीसरा अनावेशित गोला पहले तो पहले गोले के सम्पर्क में, तत्पश्चात् दूसरे गोले के सम्पर्क में लाकर, अन्त में दोनों से ही हटा लिया जाता है। अब A तथा B के बीच नया प्रतिकर्षण बल कितना होगा?
हल: 
माना प्रारम्भ में गोले A व B पर अलग समान आवेश q(q = 6.5x10^-7C) है।
माना कि तीसरा गोला है जिस पर प्रारम्भ में कोई आवेश नहीं है।
∴ प्रारम्भ में q_A = q_B = q
जब C को A के साथ सम्पर्क में रखते हैं तो A का आवेश दोनों में समान रूप से बँट जाएगा अतः
q_A' = q_C' = \(\frac{q+0}{2}=\frac{q}{2}\)
जब A से सम्पर्क कराने के बाद गोला C गोले B के सम्पर्क में रखा जायेगा तो
q_B' = q_C' = \(\frac{q+\frac{q}{2}}{2}=\frac{3}{4} q\)
अतः अब q_A' = \( \frac{q}{2}\) और q_B' = \(\frac{3}{4} q\)

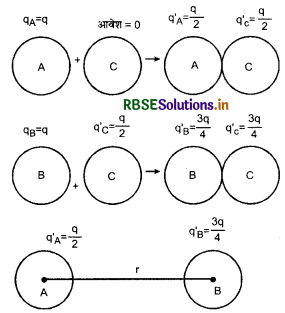
∴ प्रतिकर्षण बल

प्रश्न 14. 
चित्र में किसी एकसमान स्थिर विद्युत् क्षेत्र में तीन आवेशित कणों के पथचिह्न (tracks) दर्शाए गए हैं। तीनों आवेशों के चिह्न लिखिए। इनमें से किस कण का आवेश - संहति अनुपात (\(\frac{q}{m}\)) अधिकतम है?

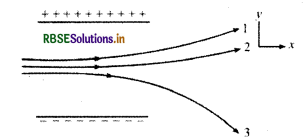
हल: 
मुख्य अभिधारणा: धनावेशित कण ऋण प्लेट की ओर तथा ऋणावेशित कण धन प्लेट की ओर विक्षेपित होते हैं।
चित्र में कण (1) व (2) धन प्लेट की ओर विक्षेपित हो रहे हैं अत: कणों (1) व (2) पर ऋणात्मक आवेश है। कण (3) ऋण प्लेट की ओर विक्षेपित हो रहा है, अतः कण (3) पर धन आवेश है। दिये गये विद्युत् क्षेत्र में कण का अभिलम्बवत् विस्थापन
y = \(\frac{1}{2}\left(\frac{q}{m}\right) \frac{\mathrm{E}_x^2}{u^2} \propto \frac{q}{m}\)
चित्र से स्पष्ट है कि कण (3) का अभिलम्बवत् विस्थापन 
अधिकतम है, अतः कण (3) के लिये \left(\frac{q}{m}\right) का मान अधिकतम है।

प्रश्न 15. 
एकसमान वैद्युत क्षेत्र 
\(\overrightarrow{\mathrm{E}}=3 \times 10^3 \hat{i} \mathrm{NC}^{-1}\) पर विचार कीजिए
(a) इस क्षेत्र का 10 cm भुजा के वर्ग के उस पाव से जिसका तल YZ तल के समान्तर है, गुजरने वाला फ्लक्स क्या है?
(b) इसी वर्ग से गुजरने वाला फ्लक्स कितना है यदि इसके तल का अभिलम्बर X - अक्ष से 60° का कोण बनाता है?
हल: 
दिया है: \(\overrightarrow{\mathrm{E}}=3 \times 10^3 \hat{i} \mathrm{NC}^{-1}\)
(a) वर्ग की भुजा l = 10 cm = 0.1m 
∴ वर्ग का क्षेत्रफल dS = l x l
= 0.1 x 0.1 = 0.01m²

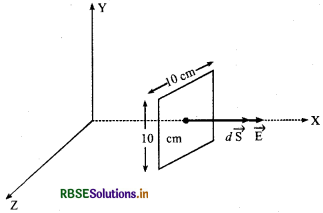
∵ विद्युत क्षेत्र X - अक्ष की दिशा में है और वर्ग का तल YZ तल में है अत: क्षेत्रफल वेक्टर d \(\overrightarrow{\mathrm{S}}\) की दिशा भी X - अक्ष की दिशा में होगी। 
अत: क्षेत्रफल वेक्टर
d \(\overrightarrow{\mathrm{S}}\) = 0.01\(\hat{i} \mathrm{~m}^2\)
∴ वर्ग के फलक से निर्गत फ्लक्स

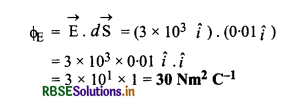
(b) इस प्रश्न में \(\overrightarrow{\mathrm{E}} \text { व } d \overrightarrow{\mathrm{S}}\) के मध्य कोण 60° है।
∴\(\phi=\overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}\)
= E.dS cos θ
= (3 x 10³).(0.01).cos60°
= 3 x 10¹ x 1/2 = 15 Nm²C^-1

प्रश्न 16. 
प्रश्न 15 में दिये गये एकसमान विद्युत् क्षेत्र का 20 cm भुजा के किसी घन से (जो इस प्रकार अभिविन्यस्त है कि उसके फलक निर्देशांक तलों के समान्तर है) कितना फ्लक्स गुजरेगा?
हल: 
एक घन में छ: फलक होते हैं। इनमें से दो फलक Y - Z तल के, दो Z - X तल के और दो X - Y तल के समान्तर होंगे।
∵ विद्युत् क्षेत्र \(\overrightarrow{\mathrm{E}}=3 \times 10^3 \hat{i} \mathrm{NC}^{-1}\) , X - अक्ष के अनुदिश है अत: Z - X व X - Y तलों के समान्तर फलों के समान्तर होगा।
∴ इन चारों फलकों से गुजरने वाला फ्लक्स शून्य होगा।
∵ विषुत् क्षेत्र एकसमान है अत: Y - Z तल के समान्तर फलकों में से जितना फ्लक्स एक फलक से अन्दर प्रवेश करेगा, उतना ही फ्लक्स दूसरे फलक से बाहर निकलेगा।
अत: घन से गुजरने वाला नेट फ्लक्स शून्य होगा।

प्रश्न 17. 
किसी काले बॉक्स के पृष्ठ पर विद्युत् क्षेत्र की सावधानीपूर्वक ली गई माप यह संकेत देती है कि बॉक्स के पृष्ठ से गुजरने वाला नेट फ्लक्स 8.0 x 10³ Nm²C^-1 है।
(a) बॉक्स के भीतर नेट आवेश कितना है?
(b) यदि बॉक्स के पृष्ठ से नेट बहिर्मुखी फ्लक्स शून्य है तो क्या आप यह निष्कर्ष निकालेंगे कि बॉक्स के भीतर कोई आवेश नहीं है? क्यों अथवा क्यों नहीं?
हल: 
(a) गाठस - प्रमेय से,

अत: घन के भीतर 0.071µC आवेश है। 

(b) पुन: गाउस प्रमेय से,
\(\phi_{\mathrm{E}}=\frac{1}{\varepsilon_0} \cdot \Sigma q\)
जहाँ  गाउसीय पृष्ठ द्वारा परिबद्ध आवेश है।
∴ \(\Sigma q=\phi_{\mathrm{E}} \cdot \varepsilon_0\)
∵ प्रश्न के अनुसार, \phi_{\mathrm{E}} = 0
∴ ∑q = 0
अर्थात् गाउसीय पृष्ठ द्वारा परिबद्ध आवेश शून्य है। इस कथन के दो अर्थ निकलते हैं-
(i) या तो पृष्ठ के अन्दर कोई आवेश नहीं है, या 
(ii) पृष्ठ (बॉक्स) के अन्दर आवेश तो है लेकिन नेट आवेश शून्य है।

प्रश्न 18. 
चित्र में 10cm भुजा के किसी वर्ग के केन्द्र से ठीक 5 cm ऊँचाई पर कोई +10µC आवेश रखा है। इस वर्ग से गुजरने वाले विद्युत् फ्लक्स का परिमाण क्या है?
(संकेत - वर्ग को 10cm किनारे के किसी घन का फलक मानिये।)

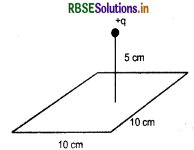
हल: 
10 cm भुजा के एक ऐसे घनाकार गाउसीय पृष्ठ की कल्पना करते हैं जिसका केन्द्र वही हो जहाँ आवेश q(10µC) रखा है। अतः गाउस के प्रमेय से गाउसीय पृष्ठ से निर्गत कुल विद्युत् फ्लक्स

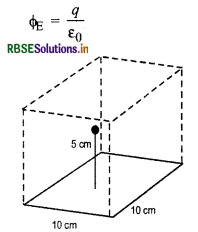
∵ घन में समान क्षेत्रफल फलक होते हैं, अतः एक फलक से निर्गत फ्लक्स

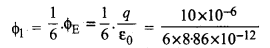
= 1.88 x 10⁵Nm²C^-1

प्रश्न 19.
2.0µC का कोई बिन्दु आवेश किसी 9.0 cm किनारे वाले किसी घनीय गाउसीय पृष्ठ के केन्द्र पर स्थित है। पृष्ठ से गुजरने वाला नेट फ्लक्स क्या है? 
हल: 
गाउस - प्रमेय से गाउसीय पृष्ठ से निर्गत वैद्युत फ्लक्स
\(\phi_{\mathrm{E}}=\frac{1}{\varepsilon_0} \times\) परिबद्ध आवेश = \(\frac{q}{\varepsilon_0}\)
दिया है:  q = 2.0µC = 2 x 10^-6C
∴\(\phi_{\mathrm{E}}=\frac{2 \times 10^{-6}}{8.854 \times 10^{-12}}\)
= 2.26 x 10⁵ Nm²C^-1

प्रश्न 20. 
किसी बिन्दु आवेश के कारण, उस बिन्दु को केन्द्र मानकर खींचे गये 10 cm त्रिज्या के गोलीय गाउसीय पृष्ठ पर विद्युत् फ्लक्स - 1.0 x 10³ Nm²C^-1है।
(a) यदि गाउसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाये तो पृष्ठ से कितना फ्लक्स गुजरेगा? 
(b) बिन्दु आवेश का मान क्या है?
हल: 
(a) गाउस के प्रमेय के अनुसार किसी बन्द गाउसीय पृष्ठ से निर्गत कुल फ्लक्स पृष्ठ द्वारा परिबद्ध आवेश पर निर्भर करता है, पृष्ठ के आकार पर नहीं। अतः पृष्ठ की त्रिज्या दोगुनी कर देने पर भी उससे निर्गत फ्लक्स पूर्ववत् रहेगा अर्थात् 

प्रश्न 21. 
10 cm त्रिज्या के चालक गोले पर अज्ञात परिमाण का आवेश है। यदि गोले के केन्द्र से 20 cm दूरी पर विद्युत् क्षेत्र 1.5 x 10³ NC^-1 त्रिज्यतः अन्तर्मुखी (radially inward) है तो गोले पर नेट आवेश कितना है?
हल: 
आवेशित गोले के केन्द्र को केन्द्र मानकर 20 cm त्रिज्या का गोलाकार गाउसीय पृष्ठ खींचते है और इस पृष्ठ पर बिन्दु P पर एक

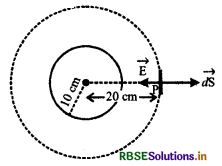
सूक्ष्म पृष्ठीय क्षेत्रफल \(\overrightarrow{d S}\) ले लेते हैं। चित्र से स्पष्ट है कि इस बिन्दु पर \(\overrightarrow{\mathrm{E}} \text { व } d \overrightarrow{\mathrm{S}}\) के मध्य 180° कोण होगा। अतः सूक्ष्म पृष्ठ से निर्गत वैद्युत फ्लक्स
\(d \phi_{\mathrm{E}}=\overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}\)
∴सम्पूर्ण गाउसीय पृष्ठ से निर्गत विद्युत् फ्लक्स

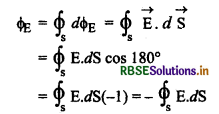
∵विद्युत् क्षेत्र की तीव्रता पूरे गोलाकार गाउसीय पृष्ठ पर समान होगी अतः

प्रश्न 22.
2.4 m व्यास के एकसमान आवेशित चालक गोले का पृष्ठीय आवेश घनत्व 80.0µCm^-2 है।
(a) गोले पर आवेश ज्ञात कीजिए। 
(b) गोले के पृष्ठ से निर्गत कुल विद्युत फ्लक्स क्या है?
हल: 
(a) समानावेशित गोले के पृष्ठ पर आवेश का पृष्ठ घनत्व
σ = \(\frac{q}{\mathrm{~A}}=\frac{q}{4 \pi r^2}\)
∴ q = 4πr2.σ
= 4 x 3.14 x 1.2 x 1.2 x 80.0 x 10^-6 C
= 1447 x 10^-6 C = 1.447 x 10^-3 C
= 1.45 x 10^-3 C

(b) गाउस के प्रमेय से यदि गोले के पृष्ठ को ही गाउसीय पृष्ठ मान लें तो गोले का समस्त आवेश परिबद्ध आवेश की श्रेणी में आयेगा। अत: पृष्ठ से निर्गत फ्लक्स
\(\phi_{\mathrm{E}}=\frac{q}{\varepsilon_0}=\frac{1.45 \times 10^{-3}}{8.854 \times 10^{-12}}\)
या Φ = 1.6 x 10⁸ Nm²C^-1

प्रश्न 23. 
कोई अनन्त रैखिक आवेश 2 cm दूरी पर 9 x 10⁴ NC^-1 विद्युत् क्षेत्र उत्पन्न करता है। रैखिक आवेश घनत्व ज्ञात कीजिए।
हल:
अनन्त विस्तार के रेखीय आवेश के कारण उत्पन्न विद्युत क्षेत्र की तीव्रता
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{2 \lambda}{r}\)
जहाँ λ आवेश का रेखीय घनत्व है और r आवेश से प्रेक्षण बिन्दु की दूरी है। 
प्रश्न से, r = 2 cm = 2 x 10^-2 m
λ = ?, E = 9 x 10⁴ NC^-1
∴ 9 x 10⁴ = 9 x 10⁹ x \(\frac{2 \lambda}{2 \times 10^{-2}}\)
∴ λ = 1.0 x 10^-7 Cm^-1
या  λ = 0.1 x 10^-6 = 0.1 µCm^-1

प्रश्न 24. 
दो बड़ी, पतली धातु की प्लेटें एक-दूसरे के समान्तर एवं निकट हैं। इनके भीतरी फलकों पर, प्लेटों के पृष्ठीय आवेश घनत्वों के चिह्न विपरीत हैं तथा इनका परिमाण 17.0 x 10^-22 Cm^-2 है।
(a) पहली प्लेट के बाहा क्षेत्र में, 
(b) दूसरी प्लेट के बाह्य क्षेत्र में तथा 
(c) प्लेटों के बीच विद्युत् क्षेत्र \(\overrightarrow{\mathrm{E}}\) का परिमाण परिकलित कीजिए। 
हल: 
दिया है, प्रत्येक प्लेट पर आवेश का पृष्ठ घनत्व
σ = 17.0 x 10^-22Cm^-2

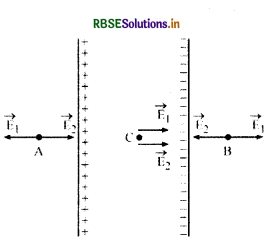
प्रत्येक प्लेट के कारण उसके निकट स्थित किसी बिन्दु पर उत्पन्न विद्युत क्षेत्र की तीव्रता
E₁ = E₂ = \(\frac{\sigma}{2 \varepsilon_0}\)
(a) पहली प्लेट के बाह्य क्षेत्र में स्थित बिन्दु A पर परिणामी विद्युत
\(\overrightarrow{\mathrm{E}}=\overrightarrow{\mathrm{E}_1}+\overrightarrow{\mathrm{E}_2}\)
या E = E₁ ~ E₂ = 0
क्योंकि \(\overrightarrow{\mathrm{E}_1} \text { व } \overrightarrow{\mathrm{E}_2}\) की दिशाएँ विपरीत हैं और परिमाण समान हैं।
(b) इसी प्रकार दूसरी प्लेट के बाह्य क्षेत्र में स्थित बिन्दु B पर परिणामी विद्युत् क्षेत्र की तीव्रता
E = E₁ ~ E₂ = 0
(c) दोनों प्लेटों के मध्य गित बिन्दुक पर दोनों प्लेटों के कारण उत्पन्न विद्युत् क्षेत्र\( \overrightarrow{\mathrm{E}_1} \text { व } \overrightarrow{\mathrm{E}_2}\) दोनों एक ही दिशा में होंगे,, अतः परिणामी विद्युत् क्षेत्र

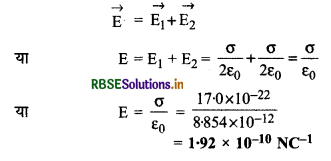
प्रश्न 25.
2.55 x 10⁴NC^-1 के नियत विद्युत क्षेत्र के प्रभाव में 12 इलेक्ट्रॉन आधिक्य की कोई तेल बूंद स्थिर रखी जाती है (मिलिकन तेल बूंद प्रयोग)। तेल का घनत्व 1.26g cm^-3 है। बूंद की त्रिज्या का आकलन कीजिए (g = 9.81 ms^-2, e = 1.60x10^-19C) 
हल: 
बूंद पर आवेश q = ne
और बूंद का द्रव्यमान m = \(\frac{4}{3} \pi r^3 \cdot \rho\)
जहाँ r बँद की त्रिज्या एवं ρ घनत्व है। 
बूँद के सन्तुलन की अवस्था में,
F_g =  F_e या m_g = E_q या \(\frac{4}{3} \pi r^3 \cdot \rho \cdot g\)= E.ne
∴ r³ = \(\frac{3 n e \mathrm{E}}{4 \pi \rho g}\)
दिया है: 
n = 12, e = 1.6 x 10^-19 C, E = 2.55 x 10⁴ NC^-1 
ρ=1.26 gcm^-3 = 1.26 x 10³ kgm^-3, g = 9.81ms^-2)
∴ \(r^3=\frac{3 \times 12 \times 1.6 \times 10^{-19} \times 2.55 \times 10^4}{4 \times 3.14 \times 1.26 \times 10^3 \times 9.81}\)
= 946 x 10^-21 m³
∴ r = (946 x 10^-21 m³)^1/3 9.81 x 10^-7 m
= 9.81 x 10^-4 mm

प्रश्न 26. 
निम्न चित्र में प्रदर्शित वक्रों में से कौन सम्भावित स्थिर विद्युत क्षेत्र रेखाएँ निरूपित नहीं करते और क्यों?

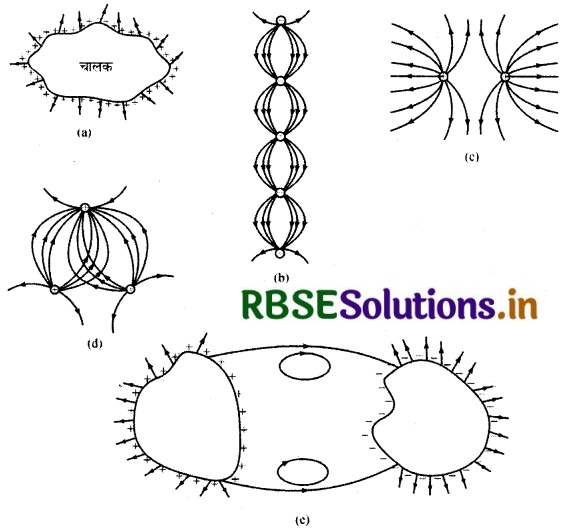
उत्तर:
केवल चित्र (c) सम्भावित विद्युत् क्षेत्र रेखाएँ निरूपित करता है।
(a) विद्युत् क्षेत्र रेखाएँ सदैव चालक पृष्ठ के लम्बवत् होती हैं, इस चित्र में रेखाएँ पृष्ठ के लम्बवत् नहीं हैं, अत: सही नहीं है।
(b) क्षेत्र रेखाओं को ऋणावेश से धनावेश की ओर प्रदर्शित किया गया है जो सही नहीं है।
(d) क्षेत्र रेखाएं एक-दूसरे को काट रही हैं जो कि सही नहीं हैं।
(e) क्षेत्र रेखाएँ क्षेत्र बन्द वक्रों के रूप में दिखायी गई है जो कि सही नहीं हैं।

प्रश्न 27. 
दिकस्थान के किसी क्षेत्र में, विद्युत् क्षेत्र सभी जगह z - दिशा के अनुदिश है, परन्तु विद्युत् क्षेत्र का परिमाण नियत नहीं है, इसम एकसमान रूप से z - दिशा के अनुदिश 105NC^-1m^-1 की दर से वृद्धि होती है। वह निकाय जिसका z - दिशा में कुल ऋणात्मक द्विध्रुव आघूर्ण 10^-7 Cm के बराबर है, कितना बल तथा बल - आघूर्ण अनुभव करता है?
हल: 
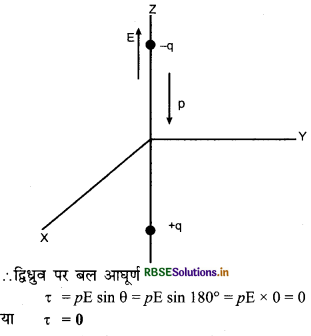
प्रश्न के अनुसार, वैद्युत द्विध्रुव z - अक्ष के अनुदिश संरेखित है, अतः
P_x  = 0,P_y = 0,P_z = -10^-7 Cm 
विद्युत् क्षेत्र का परिवर्तन z - दिशा में होता है अत:
\(\frac{\partial \mathrm{E}}{\partial x}=0, \frac{\partial \mathrm{E}}{\partial y}=0, \frac{\partial \mathrm{E}}{\partial z}=10^5 \mathrm{NC}^{-1} \mathrm{~m}^{-1}\)
अत: द्विध्रुव पर बल
\(\mathrm{F}=p_x \cdot \frac{\partial \mathrm{E}}{\partial x}+p_y \cdot \frac{\partial \mathrm{E}}{\partial y}+p_z \frac{\partial \mathrm{E}}{\partial z}\)
= 0 + 0 + (-10 ^-7)(10⁵)
= -1 x 10^-2 N 
या F = -0.01N (Z - अक्ष को ऋण दिशा में) 
पुनः प्रश्न के अनुसार वैद्युत क्षेत्र की दिशा Z - अक्ष के अनुदिश है और \(\vec{p}\) को दिशा -Z - अक्ष के अनुदिश है, अत: दोनों के मध्य कोण θ = 180°

प्रश्न 28.
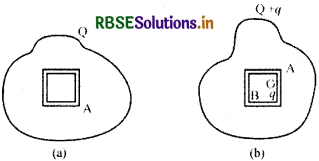
(a) किसी चालक A, जिसमें प्रस्तुत चित्र (a) के अनुसार कोई कोटर/गुहा (cavity) है, को Q आवेश दिया गया है। यह दर्शाइए कि समस्त आवेश चालक के बाह्य पृष्ठ पर प्रतीत होना चाहिए। 
(b) कोई अन्य चालक B, जिस पर q आवेश है, को कोटर/गुहा में इस प्रकार घुसा दिया जाता है कि चालक B चालक A से विद्युतरोधी रहे। यह दर्शाइए कि चालक A के बाह्य पृष्ठ पर कुल आवेश (Q+q) है|चित्र (b)]।
(c) किसी सुग्राही उपकरण को उसके पर्यावरण के प्रबल स्थिर विद्युत् क्षेत्रों से परिरक्षित (shield) किया जाना है। सम्भावित उपाय लिखिए।

उत्तर:
(a) एक ऐसे गाउसीय पृष्ठ की कल्पना करते हैं जो पूर्णत: चालक A के अन्दर है और चालक के बाहा पृष्ठ के अत्यन्त समीप है। चूँकि आवेशित चालक के अन्दर विद्युत् क्षेत्र शून्य (अर्थात् E = 0) होता है, अतः गाउसीय पृष्ठ से निर्गत विद्युत् फ्लक्स शून्य होगा अर्थात्
Φ = 0
परन्तु Φ = \(\frac{q}{\varepsilon_0}\) ⇒ q = Φε₀ = 0
अर्थात् सतह के अन्दर आवेश शून्य होगा। फलस्वरूप चालक का समस्त आवेश Q उसके पृष्ठ पर वितरित होगा। 

(b) प्रश्नानुसार,
चालक A पर कुल आवेश = Q 
और चालक B पर कुल आवेश = q
माना चालक A के अन्दर बने कोटर के पृष्ठ पर आवेश q1 है और चालक A के आय पृष्ठ पर आवेश Q₁ है तो चालक A पर कुल आवेश
Q = Q₁ + q₁
या Q₁ + q₁ = Q ..........(i)
पुन: एक ऐसे गाउसीय पृष्ठ की कल्पना करते हैं जो पूर्णत: चालक A के अन्दर हो और इसके बाह्य पृष्ठ के अत्यन्त समीप हो। चूंकि आवेशित चालक के अन्दर E = 0 होता है अत: चालक के अन्दर कुल आवेश = 0 होगा अर्थात्
q₁ + q = 0
⇒ q₁ = -q
∴ समीकरण (i) से,
Q₁ - q = Q
या Q₁ = (Q + q)

(c) खोखले बन्द चालक के अन्दर विद्युत् क्षेत्र शून्य होता है, अत: किसी सुग्राही उपकरण को पर्यावरण के प्रबल स्थिर - विद्युत् क्षेत्रों से परिरक्षित करने के लिए उसे बन्द खोखले चालक के अन्दर रखना होगा।

प्रश्न 29. 
किसी खोखले आवेशित चालक में उसके पृष्ठ पर कोई छिद बनाया गया है। यह दर्शाइए कि छिद में विद्युत् क्षेत्र \(\left(\frac{\sigma}{2 \varepsilon_0}\right)\) \(\hat{n}\) है, जहाँ \hat{n} अभिलम्बवत् दिशा में बहिर्मुखी एकांक वेक्टर है तथा σ छिद के निकट आवेश का पृष्ठ घनत्व है।
उत्तर:
माना किसी खोखले चालक को कुछ धनावेश दिया जाता है जो उसके पृष्ठ पर समान रूप से वितरित हो जायेगा और पृष्ठ पर आवेश का पृष्ठ घनत्व σ है।

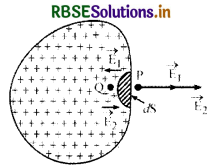
चालक पर किसी क्षेत्रफल अल्पांश dS पर विचार करते हैं। इस अल्पांश पर आवेश की मात्रा σ.dS होगी। माना इस क्षेत्रफल अल्पांश के अति समीप पृष्ठ के बाहर एवं भीतर बिन्दु क्रमशः P व Q हैं। बिन्दु P पृष्ठ के बाहर है अत: इस पर चालक के कारण विद्युत् क्षेत्र की तीव्रता E= \(\frac{\sigma}{\varepsilon_0}\) पृष्ठ के लम्बवत् बाहर की ओर होगी। माना P पर क्षेत्रफल अल्पांश dS व शेष पृष्ठ के कारण विद्युत् क्षेत्र की तीव्रताएँ क्रमश: E₁ व E₂ हैं। ये दोनों क्षेत्र पृष्ठ के लम्बवत् बाहर की ओर होंगे अतः
E₁ + E₂ = \(\frac{\sigma}{\varepsilon_0}\)  .........(i)
बिन्दुए Q पृष्ठ के अन्दर है और क्षेत्रफल अल्पांश dS के अति समीप तथा P के विपरीत ओर है, अत: क्षेत्रफल अल्यांश के कारण विद्युत् क्षेत्र E₁ एवं शेष पृष्ठ के कारण E₂ परस्पर विपरीत दिशा में होंगे और आवेशित चालक के अन्दर परिणामी विद्युत् क्षेत्र E = 0 होता है, अत: Q पर परिणामी विद्युत् क्षेत्र
E₂ - E₁ = 0
या E₁ = E₂
अतः समीकरण (i) से,

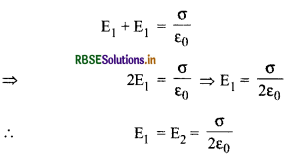
अतः शेष चालक के कारण बिन्दु P पर विद्युत् क्षेत्र की तीव्रता
E₂ = \(\frac{\sigma}{2 \varepsilon_0}\)
अब यदि बिन्दु पर एक छिद कर दिया जाये तो क्षेत्रफल अल्पांश dS तथा इसके कारण आन्तरिक बिन्दु Q पर विद्युत् क्षेत्र E₁ दोनों जगह समाप्त हो जायेंगे।
इस प्रकार किसी बिन्दु पर विद्युत् क्षेत्र केवल E₂ शेष रहेगा। अत: छिद्र पर विद्युत् क्षेत्र की तीव्रता
\(\overrightarrow{\mathrm{E}}=\frac{\sigma}{2 \varepsilon_0} \hat{n}\)
जहाँ \(\hat{n}\) छिद पर बाहर की दिशा में एकांक वेक्टर है।

प्रश्न 30. 
गाउस नियम का उपयोग किये बिना किसी एकसमान रैखिक आवेश घनत्व λ के लम्बे पतले तार के कारण विद्युत् क्षेत्र के लिए सूत्र प्राप्त कीजिए।
उत्तर:
माना एक अनन्त लम्बाई के धनावेशित रैखिक चालक के निकट r दूरी पर चालक के कारण उत्पन्न विद्युत् क्षेत्र की तीव्रता ज्ञात करनी है। चालक पर आवेश का रेखीय घनत्व λ है। बिन्दु P के सम्मुख बिन्दु O से एक ओर x दूरी पर dx लम्बाई का एक अल्पांश AB ले लेते हैं। इस अल्पांश पर आवेश का मान λ.dx होगा। इस अल्पांश के कारण P बिन्दु पर AP दिशा में विद्युत् क्षेत्र dE उत्पन्न↨होता है। इसी प्रकार O के दूसरी ओर इतनी ही दूरी पर स्थित आवेश अल्पांश के करण dE विद्युत् क्षेत्र उत्पन्न होगा। इन दोनों के OP दिशा में घटक dE cosθ जुड़कर विद्युत् क्षेत्र प्रदान करेंगे और लम्ब घटक dE sin θ एक - दूसरे को निरस्त कर देंगे। 
∴ अल्पांश AB पर आवेश
dq =  λ.dx
अतः इस आवेश के कारण P पर विद्युत् क्षेत्र की तीव्रता 
dE =  (AP दिशा में) 
OP दिशा में पूरे तार के कारण P पर उत्पन्न विद्युत् क्षेत्र को तीव्रता
E = Σ dEcosθ

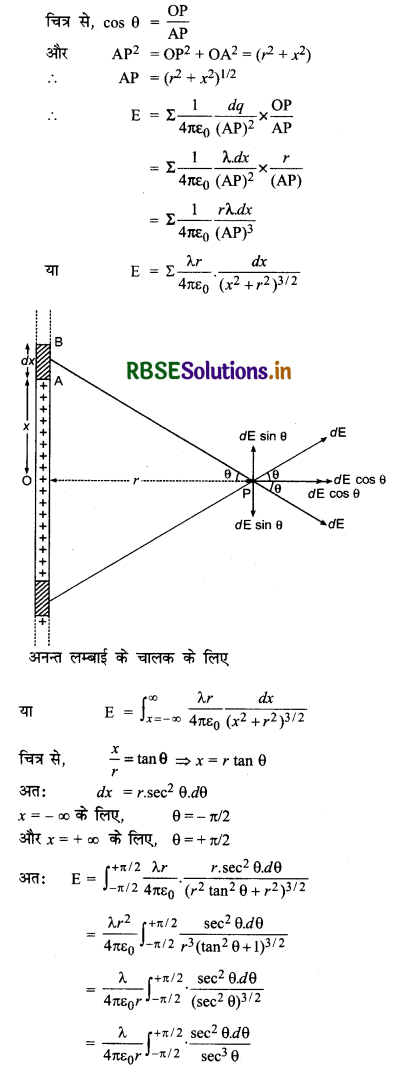
प्रश्न 31.
अब ऐसा सिद्ध हो चुका है कि स्वयं प्रोटॉन एवं न्यूट्रॉन (जो सामान्य द्रव्य के नाभिकों का निर्माण करते है और अधिक मूल इकाइयों, जिन्हें क्वार्क कहते हैं, के बने हैं। प्रत्येक प्रोटॉन तथा न्यूट्रॉन तीन क्वाकों से मिलकर बनता है। दो प्रकार के क्वार्क होते हैं- 'अप क्वार्क' (u द्वारा निर्दिष्ट) जिन पर +\(\left(\frac{2}{3}\right)\) e आवेश तथा 'डाउन क्वार्क' (व द्वारा निर्दिष्ट) जिन पर -\(\left(\frac{1}{3}\right)\)e आवेश होता है, इलेक्ट्रॉन से मिलकर सामान्य द्रव्य बनाते हैं। (कुछ अन्य प्रकार के क्वार्क भी पाये गये हैं जो भिन्न असामान्य प्रकार का द्रव्य बनाते हैं।) प्रोटॉन तथा न्यूट्रॉन के सम्भावित क्वार्क संघटन सुझाइए।
हल: 
दिया है: 
अप क्वार्क पर आवेश u = +\(\left(\frac{2}{3}\right)\) e
और डाउन क्वार्क पर आवेश
d = -\(\left(\frac{1}{3}\right)\) e
∵ प्रोटॉन पर कुल आवेश = \(-\frac{1}{3}\)e
= + e
=\(+\frac{2}{3} u +\frac{2}{3} u -\frac{1}{3} d \)
= u + u + d = 2u + d
∴ 2u + d = +e
अतः प्रोटॉन 2u क्वार्क तथा 1d क्वार्क से मिलकर बना है। 
इसी प्रकार न्यूट्रॉन पर आवेश = 0
= \(+\frac{2}{3} u -\frac{1}{3} u -\frac{1}{3} d\)
= u + d + d = u + 2d
u + 2d 
या u + 2d = 0
अत: न्यूट्रॉन एक u क्वार्क तथा एक 2d क्वार्क से मिलकर बना है।

प्रश्न 32. 
(a) किसी यादृच्छिक स्थिर विद्युत् क्षेत्र विन्यास पर विचार कीजिए। इस विन्यास की किसी शून्य - विक्षेप स्थिति (nullpoint अर्थात् जहाँ \(\overrightarrow{\mathrm{E}}\) = 0) पर कोई छोटा परीक्षण आवेश रखा गया है। यह दर्शाइए कि परीक्षण आवेश का सन्तुलन आवश्यक रूप से अस्थायी है।
(b) इस परिणाम का समान परिमाण तथा चिह्नों के दो आवेशों (जो एक - दूसरे से किसी दूरी पर रखे है) के सरल विन्यास के लिए सत्यापन कीजिए।
उत्तर:
(a) माना शून्य विक्षेप स्थिति में रखे परीक्षण आवेश का सन्तुलन स्थायी है। अब यदि परीक्षण आदेश को सन्तुलन स्थिति से थोड़ा - सा विस्थापित किया जाये तो परीक्षण आवेश पर एक प्रत्यानयन बल लगना चाहिए जो उसे वापस सन्तुलन स्थिति की ओर ले जाये। इसका अर्थ यह हुआ कि उस स्थान पर शून्य विक्षेप बिन्दु की ओर जाने वाली क्षेत्र रेखाएँ होनी चाहिए, जबकि स्थिर विद्युत् - क्षेत्र रेखाएँ कभी भी शुन्य विक्षेप बिन्दु तक नहीं पहुँची। अत: हमारी यह परिकल्पना कि परीक्षण आवेश का सन्तुलन स्थायी है, गलत है। यह निश्चित रूप से अस्थायी सन्तुलन है।

(b) माना दो बिन्दु आवेश (प्रत्येक +q) A व B पर रखे हैं और इन बिन्दुओं के मध्य दूरी 2a है। A व B के मध्य - बिन्दु C पर एक बिन्दु आवेश -Q रखा है।
बिन्दु आवेश -Q पर A व B पर रखे +q आवेशों के कारण लगने वाले बल \(\overrightarrow{\mathrm{F}_1} \text { व } \overrightarrow{\mathrm{F}_2}\) परिमाण में समान एवं दिशा में विपरीत होने के कारण एक - दूसरे को निरस्त कर देंगे। फलस्वरूप -Q आवेश सन्तुलन में रहेगा।

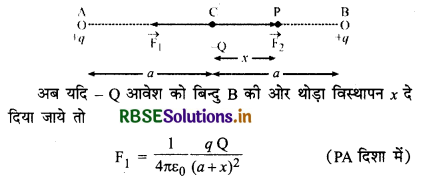
और F₂ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q \mathrm{Q}}{(a-x)^2}\)  (PB दिशा में) 
स्पष्ट है कि F₂ > F₁
आत: -Q आवेश पर परिणामी बल (F₂ - F₁) PB दिशा में लगेगा जो इसे सन्तुलन स्थिति C से और दूर ले जायेगा। इस प्रकार आवेश (-Q) का मध्य - बिन्दु C पर सन्तुलन अस्थायी है।

प्रश्न 33. 
प्रारम्भ में x - अक्ष के अनुदिश vx चाल से गति करता हुआ, दो आवेशित प्लेटों के मध्य क्षेत्र में m द्रव्यमान तथा -q आवेश का एक कण प्रवेश करता है। प्लेटों की लम्बाई L है। इन दोनों प्लेटों के बीच एकसमान विद्युत क्षेत्र E बनाये रखा जाता है। दर्शाइए कि प्लेट के अन्तिम किनारे पर कण का ऊधिर विक्षेप\( \frac{q E L^2}{\left(2 m v_x^2\right)}\) है। साथ ही गुरुत्वीय क्षेत्र में प्रक्षेप्य गति के साथ इस कण की गति की तुलना कीजिए।
उत्तर:
एकसमान विद्युत् क्षेत्र में आवेशित कण का गमन - पथ जबकि कण का प्रारम्भिक वेग विद्युत् क्षेत्र की दिशा के लम्बवत् हो - माना कोई आवेश (-q) वेग vx से किसी विद्युत् क्षेत्र E में क्षेत्र के लम्बवत् प्रवेश करता है। क्षेत्र E की दिशा Y - अक्ष के अनुदिश है और आवेश का प्रारम्भिक वेग X - अक्ष के अनुदिश है। यदि आवेश -q है तो कण पर एक वैद्युत बल F = qE वैद्युत क्षेत्र की विपरीत दिशा में लगेगा और कण पर Y - दिशा में एक त्वरण कार्य करेगा। चौक कण का प्रारम्भिक वेग विद्युत् क्षेत्र के लम्बवत् है अत: वैद्युत बल के कारण vx में कोई परिवर्तन नहीं होगा। सुविधा के लिए विद्युत् क्षेत्र में प्रवेश बिन्दु को ही हमने मूल बिन्दु मान लिया है और प्लेटों की लम्बाई x ली है। माना t सेकण्ड बाद कण के निर्देशांक (x,y) हैं तो

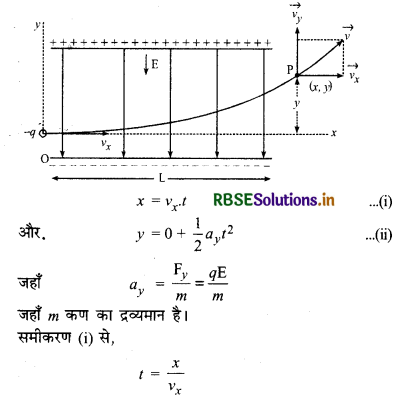
समी. (ii) में t का मान रखने पर,

यह समीकरण y = ax² रूप का है जो कि परवलय का समीकरण है। अत: वैद्युत क्षेत्र के लम्बवत् प्रवेश करने वाले आवेश का पथ परवलयाकार होता है।
यदि प्लेटों की लम्बाई L हो तो x = L 
अतः समीकरण (iii) निम्न स्वरूप में होगा-
y = \(\left(\frac{q \mathrm{E}}{2 m v_x^2}\right) \mathrm{L}^2=\left(\frac{q \mathrm{EL}^2}{2 m v_x^2}\right)\)
अतः प्लेटों के दूसरे किनारे पर कण का ऊधिर विक्षेप \(\left(\frac{q \mathrm{EL}^2}{2 m v_x^2}\right)\) होगा।

प्रश्न 34. 
प्रश्न 33 में वर्णित कण की इलेक्ट्रॉन के रूप में कल्पना कीजिए जिसको vx = 2.0 x 10⁶ms^-1 के साथ प्रक्षेपित किया गया है। यदि 0.5cm की दूरी पर रखी प्लेटों के बीच विद्युत् क्षेत्र E का मान 9.1 x 10²NC^-1 हो तो ऊपरी प्लेट पर इलेक्ट्रॉन कहाँ टकरायेगा? 
\(\left.|| e \mid=1.6 \times 10^{-19} \mathrm{C}, m_e=9 \cdot 1 \times 10^{-31} \mathrm{~kg}\right]\)
हल: 
Y - दिशा में आवेशित कण का विस्थापन
y = \(\frac{q \mathrm{E}}{2 m v_x^2} \cdot x^2 ⇒ x2 = \frac{2 m v_x^2}{q \mathrm{E}} \cdot y\)
​यहाँ q = e = 1.6 x 10^-19C, E = 9.1 x 10^-2 NC^-1
v_x = 2.0 x 10⁶ ms^-1, m_e = 9.1 x 10^-31 kg 
यदि इलेक्ट्रॉन का प्रवेश प्लेटों के मध्य - बिन्दु पर हो तो
अत: इलेक्ट्रॉन ऊपरी प्लेट से 1.12 cm की दूरी पर टकरायेगा।