RBSE Solutions for Class 12 Physics Chapter 1 Electric Charges and Fields

Rajasthan Board RBSE Solutions for Class 12 Physics Chapter 1 Electric Charges and Fields Textbook Exercise Questions and Answers.

RBSE Class 12 Physics Solutions Chapter 1 Electric Charges and Fields

RBSE Class 12 Physics Electric Charges and Fields Textbook Questions and Answers

Question 1.1.
What is the force between two small charged spheres having charges of 2 x 10^-7 C and 3 x 10^-7 C placed 30 cm apart in air?
Answer:
Given q₁ = 2 x 10^-7 C, q₂ = 3 x 10^-7 C, r = 30 cm = 0.3 m
∴ Force of repulsion, F = 9 x 10⁹ x \(\frac{q_1 q_2}{r^2}\)
= 9 x 10⁹ x \(\frac{2 \times 10^{-7} \times 3 \times 10^{-7}}{(0.3)^2}=\frac{54 \times 10^{-5}}{9 \times 10^{-2}}\)
= 6 x 10^-3 N

Question 1.2.
The electrostatic force on a small sphere of charge 0.4 µC due to another small sphere of charge -0.8 µC in air is 0.2 N.
(a) What is the distance between the two spheres?
(b) What is the force on the second sphere due to the first?
Answer:
Given q₁ = 0.4 µC = 0.4 x 10^-6 C
q₂ = - 0.8 µC = - 0.8 x 10^-6 C
F = 0.2 N, r = ?

(a) Since F = 9 x 10⁹ x \(\frac{q_1 q_2}{r^2}\)
or 0.2 = \(\frac{9 \times 10^9 \times\left(0.4 \times 10^{-6}\right)\left(0.8 \times 10^{-6}\right)}{r^2}\)
or r² = \(\frac{9 \times 10^9 \times 0.32 \times 10^{-12}}{0.2}\)
or r = 12 x 10^-2 m = 12 cm

(b) The second sphere will attract the first with the same force i.e. force of 0.2 N.

Question 1.3.
Check that the ratio ke²/Gm_em_p is dimensionless. Look up a table of physical constants and determine the value of this ratio. What does the ratio signify?
Answer:
Since F_e = \(-\frac{k e^2}{r^2}\) .................(1)
So k_e² = -F_er²
And    F_G = -G\(\frac{m_p m_e}{r^2}\) ................(2)
So dimensions of \(\frac{k e^2}{\mathrm{G} m_e m_p}=\frac{\mathrm{F}_e r^2}{\mathrm{~F}_{\mathrm{G}} r^2}=\frac{\mathrm{F}_e}{\mathrm{~F}_{\mathrm{G}}}\)
= \(\frac{\left[\mathrm{MLT}^{-2}\right]}{\left[\mathrm{MLT}^{-2}\right]}\) = [M⁰L⁰T⁰]
= No dimensions
The value of \(\frac{k e^2}{\mathrm{G} m_e m_p}\)
= \(\frac{9 \times 10^9 \times\left(1.6 \times 10^{-19}\right)^2}{6.67 \times 10^{-11}\left(1.67 \times 10^{-27}\right)\left(9.1 \times 10^{-31}\right)}\)
From  Eq. (1) and (2), we have
\(\left|\frac{\mathrm{F}_e}{\mathrm{~F}_\theta}\right| = \frac{k e^2}{\mathrm{G} m_p m_e}\) = 2.9 x 10³⁹
The ratio of the two forces shows that electrical forces are enormously stronger than the gravitational forces.

Question 1.4.
(a) Explain the meaning of the statement 'electric charge of a body is quantised.'
(b) Why can one ignore quantisation of electric charge when dealing with macroscopic i.e,large scale charges?
Answer:
(a) Quantisatin of charge. It is that property of charge by virtue of which charge on a body exists in the form of discrete packet of charge e, only, where e is the charge on a electron. The charge carried by anybody would be equal to ±ne, where n = 0, 1, 2, 3, 4, 5, etc. The charge on a body is thus some multiple of e and cannot exist as a fraction of e. So charge exists in the form of packets and not in continuous amounts. Thus, charge is said to have a discrete (discontinuous) nature or is said to be quantised.

(b) At macroscopic level, we deal with charges that are enormous as compared to the magnitude of minimum charge i.e. e (1.6 x 10^-19 C). In this case, the increase and decrease in units of e is not very different from saying that charges are continuous. So at macroscopic level we can ignore quantisation of electric charge.

Question 1.5.
When a glass rod is rubbed with a silk cloth, charges appear on both. A similar  phenomenon is observed with many other pairs of bodies. Exaplain how this observation is consistent with the law of conservation  of charge.
Answer:
When a glass rod is rubbed with silk, the charges developed on the glass rod and the piece of silk are equal and opposite. Similar is the case in other pair of bodies. So electric charge can neither be produced nor destroyed but simply transferred from one body to another, hence is consistent with the law of conservation of charge.

Question 1.6.
Four point charges q_A = 2 µC, q_B = -5 µC, q_C = 2 µC, q_D = -5 µC are located at the corners of a square ABCD of side 10 cm. What is the force on a charge of 1 µC placed at the centre of the square?
Answer:
ABCD is a square having charges q_A = 2 µC, q_B = -5 µC, q_C = 2 µC, q_D = -5 µC at its corners and a charge 1 µC is placed at the centre O.
AO = \(\frac{1}{2} AC = \frac{1}{2} \sqrt{10^2+10^2}\)
or AO = \(\frac{10}{\sqrt{2}}\) cm = x (say)

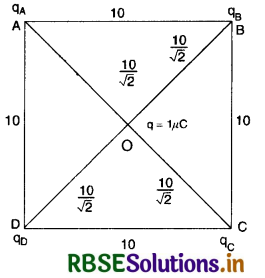
Force on q due to q_A
|F₁| = \(\frac{9 \times 10^9 \times 2 \times 10^{-6} \times 10^{-6}}{\left(\frac{10}{\sqrt{2}} \times 10^{-2}\right)^2}\)
= 3.6 N along OC
Force on q due to q_C
|F₂| = \(\frac{9 \times 10^9 \times 2 \times 10^{-6} \times 10^{-6}}{\left(\frac{10}{\sqrt{2}} \times 10^{-2}\right)^2}\)
= 3.6 N along OA
∴ Net force on q due to q_A and q_C = 0
Force on q due to q_B
|F₃| = \(\frac{9 \times 10^9 \times\left(5 \times 10^{-6}\right) \times 10^{-6}}{\left(\frac{10}{\sqrt{2}} \times 10^{-2}\right)^2}\)
= 9 N along OB
Force on q due to q_D
|F₄| = \(\frac{9 \times 10^9 \times\left(5 \times 10^{-6}\right) \times 10^{-6}}{\left(\frac{10}{\sqrt{2}} \times 10^{-2}\right)^2}\)
= 9 N along OD
∴ Net force on q due to q_B and q_D = 0
So net force on q due to four charges is zero.

Question 1.7.
(a) An electrostatic field line is a continuous curve. That is, a field line cannot have sudden break. Why not?
(b) Explain why two field lines never cross each other at any point.
Answer:
(a) The electric line of force starts from a positively charged body and ends at a negatively charged body and it carries information about the direction of electric field at different points in space, thus it cannot have sudden break.

(b) Because if any two lines cross each other at any point, then the electric field at the point of intersection will not have a unique direction, which is impossible. Hence no two electric lines of force can intersect each other.

Question 1.8.
Two point charges q_A = 3 µC and q_B = -3 µC are located 20 cm apart in vacuum.
(a) What is the electric field at the mid point O of the line AB joining the two charges?
(b) If a negative test charge of magnitude 1.5 x 10^-9 C is placed at this point, what is the force exprienced by the test charge?
Answer:
Given,
q_A = 3 µC = 3 x 10^-6 C
q_B = -3 µC = -3 x 10^-6 C

(a) Electric field at O due to q_A
E_A = \(\frac{9 \times 10^9 \times 3 \times 10^{-6}}{0.01}\) = 2.7 x 10⁶ NC^-1 along OB

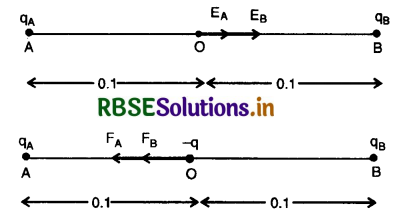
Electric field at O due to q_B
E_B = \(\frac{9 \times 10^9 \times 3 \times 10^{-6}}{0.01}\)
or E_B = 2.7 x 10⁶ NC^-1 along OB
Total electric field at O due to qA and qB 
E = E_A + E_B
= 2.7 x 10⁶ + 2.7 x 10⁶ 
= 5.4 x 10⁶ NC^-1 along OB

(b) If a charge - q = 1.5 x 10^-9 C is placed at O, then Force acting on - q due to q_A
F_A = \(\frac{9 \times 10^9 \times 3 \times 10^{-6} \times 1.5 \times 10^{-9}}{0.01}\)
= 4.05 x 10^-3 N along OA
∴ Total Force acting on - q due to q_A and q_B
F = F_A + F_B = 4.05 x 10^-3 + 4.05 x 10^-3
= 8.1 x 10^-3 N along OA

Question 1.9.
A system has two charges q_A = 2.5 x 10^-7 C and q_B = -2.5 x 10^-7 C located at A: (0, 0, -15 cm) and B: (0, 0, +15 cm) respectively. What is the total charge and electric dipole of the system?
Answer:
Since electric dipole consists of two equal and opposite charges,
Hence total charge = q_A + q_B = 0

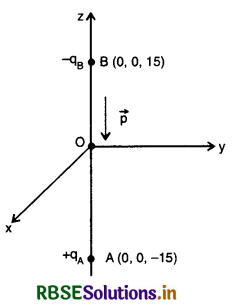
Diploe moment, \(\vec{p} = q (2\vec{a})\) along - z - axis
where q = q_A = q_B = 2.5 x 10^-7 C
2a = 30 cm = 0.3 m
So \(\vec{p}\) = 2.5 x 10^-7 x 0.3
or \(\vec{p}\) = 7.5 x 10^-8 cm along - z - axis

Question 1.10.
An electric dipole with dipole moment 4 x 10^-9 C m is aligned at 30° with the direction of a uniform electric field of magnitude 5 x 10⁴ NC^-1. Calculate the magnitude of the torque acting on the dipole.
Answer:
Given p = 4 x 10^-9 Cm, θ = 30°, E = 5 x 10⁴ NC^-1, r = ?
Since τ = pEsinθ = 4 x 10^-9 x 5 x 10⁴ x sin30°
= 20 x 10^-5 x \(\frac{1}{2}\) = 10^-4 Nm

Question 1.11.
A polythene piece rubbed with wool is found to have a negative charge of 3 x 10^-7 C.
(a) Estimate the number of electrons transferred (from which to which).
(b) Is there a transfer of mass from wool to polythene?
Answer:
(a) Charge on one electron = 1.6 x 10^-19 C
∴ Number of electrons in the given charge
n = \(\frac{q}{e}=\frac{3 \times 10^{-7}}{1.6 \times 10^{--19}}\) = 1.875 x 10¹² = 2 x 10¹²

(b) Since wool gets negative charge on rubbing with polythene, wool must gain electrons from polythene.
∴ Ideally speaking there must be a transfer of mass due to transfer of electrons but since the mass of electron is very small, this transfer of mass may be negligible (= 2 x 10^-18 kg)

Question 1.12.
Two insulated charged copper spheres A and B have their centres separated by a distance of 50 cm.
(а) What is the mutual force of electrostatic repulsion if the charge on each is 6.5 x 10^-7 C? The radii of A and B are negligible as compared to the distance of separation.
(b) What is the force of repulsion if each sphere is charged double the above amount and the distance between them is halved?
Answer:
(a) q₁ = 6.5 X 10^-7 C, q₂ = 6.5 X 10^-7 C, r = 50 cm = 0.50 m
F = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2}=\frac{9 \times 10^9 \times 6.5 \times 10^{-7} \times 6.5 \times 10^{-7}}{(0.50)^2}\)
= 1.52 x 10^-2 N

(b) When each charge is doubled and the distance between them is reduced to half, then
F = \(\frac{1}{4 \pi \varepsilon_0} \frac{\left(2 q_1\right)\left(2 q_2\right)}{(r / 2)^2}=16 \cdot \frac{1}{4 \pi \varepsilon_0} \cdot \frac{q_1 q_2}{r^2}\)
= 16 x 1.52 x 10^-2 = 0.24 N

Question 1.13.
Suppose the spheres A and B in Q. 1.10 have identical sizes. A third sphere of the same size but uncharged is brought in contact with the first, then brought in contact with the second and finally removed from both. What is the new force of repulsion between A and B?
Answer:
Let A and B be two given spheres each having charge q = 6.5 X 10^-7 C. When another sphere say C is placed in contact with the sphere A, the two will distribute the charges equally, Fig. TBQ 1.13 (a).

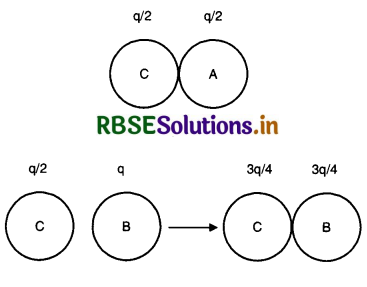
When C (with charge of q/2) is placed in contact with B, they again share charges till their potentials are equal and hence their charges are equal (their capacities are equal).
Charge on each = \(\frac{1}{2}\left(q+\frac{q}{2}\right)=\frac{3}{4}\) q
Finally, charge on A = \(\frac{q}{2}\) , Charge on B = \(\frac{3 q}{4}\), Distance = 0.50 m
Force, F = 9 x 10⁹ x \(\frac{\left(\frac{q}{2}\right)\left(\frac{3 q}{4}\right)}{(0.50)^2}\)
= \(\frac{3}{8}\left[9 \times 10^9 \times \frac{q^2}{(0.50)^2}\right]\)
or F = \(\frac{3}{8}\) x 1.52 x 10^-2 N.
= 5.7 x 10^-3 N.

Question 1.14.
Figure TBQ 1.14 gives tracks of three charged particles in a uniform electrostatic field. Given the signs of the three charges. Which particle has the highest charge to mass ratio?

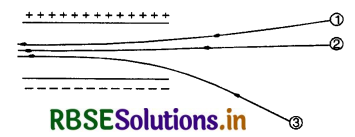
Answer:
Charges 1 and 2 are negative because the deflections are towards +vely charged plate. Particle 3 has the +ve because charge is defleted towards -vely charged plate. Particle 3 has the highest charge to mass ratio because the greater is the charge on the particle (or lesser is its mass) the more is its deflection.

Question 1.15.
Consider a uniform electric field 
\(\overrightarrow{\mathrm{E}}\) = 3 x 10³ \(\hat{i}\) N/C
(a) What is the flux of this field through a square of 10 cm on a side whose plane is parallel to yz - plane?
(b) What is the flux through the same square if the normal to its plane makes a 60° angle with the x - axis?
Answer:
Given, \(\overrightarrow{\mathrm{E}}\) = 3 x 10³ \(\hat{i}\) N/C (i.e. along x - axis)
dS = 10 x 10 = 100 cm² = 0.01 m²
(a) Here θ = 0°
∴ Flux Φ = E dS cos 0°
= E dS = 3 x 10³ x (0.01) = 30 Nm²C^-1
(b) Here θ = 60°
∴ Flux Φ = E dS cos 60° = 30 x \(\frac{1}{2}\) = 15 Nm² C^-1

Question 1.16.
What is the net flux of the uniform electric field of Exercise 1.15 through a cube of side 20 cm oriented so that its faves are parallel to the coordinate planes.
Answer:
Net flux over the cube is zero, because the number of lines entering the cube is the same as the number of lines leaving the cube.

Question 1.17.
Careful measurement of the electric field at the surface of a black box indicates that the net outward flux through the surface of the box is 8.0 x 10³ Nm²/C
(a) What is the net charge inside the box?
(b) If the net outward flux through the surface of the box were zero, could you conclude that there were no charges inside the box? Why or why not?
Answer:
(a) Given
Φ = 8.0 x 10³ Nm² C^-1, q = ?
Since Φ = \(\frac{q}{\varepsilon_0}\)
∴ q = ε₀Φ = 8.854 x 10^-12 x 8.0 x 10³
= 0.07 x 10^-6 C = 0.07 µC

(b) No, only the net charge inside is zero.

Question 1.18.
A point charge +10 µC is at a distance 5 cm directly above the centre of a square of side 10 cm as showm in the figure. What is the magnitude of the electric flux through the square.
[Hint. Think of the square on one face of a cube with edge 10 cm]
Answer:
Here we can imagine that the square ABCD as one face of a cube with edge 0 cm, and charge +q is placed at the centre of the cube as shown in the figure.
From Gauss' theorem, electrix flux through all the faces of the cube
Φ = \(\frac{q}{\varepsilon_0}\)

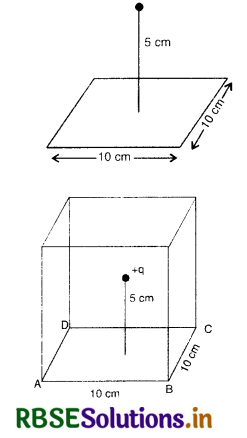
∴ Electrix flux through the square
Φ_e = \(\frac{1}{6} \frac{q}{\varepsilon_0}\)
= \(\frac{1}{6} \times \frac{10 \times 10^{-6}}{8.85 \times 10^{-12}}\)
= 1.88 x 10⁵ Nm² C^-1

Question 1.19.
A point charge of 2.0 µC is at the centre of a cubic Gaussian surface 9.0 cm on edge. What is the net electrix flux through the surface?
Answer:
q = 2.0 µC = 2 x 10^-6 C
∴ Net flux Φ = \(\frac{q}{\varepsilon_0}\)
= \(\frac{2 \times 10^{-6}}{8.854 \times 10^{-12}}\) = 2.26 x 10⁵ Nm² C^-1

Question 1.20.
A point charge causes an electric flux of -1.0 x 10³ Nm² C^-1 to pass through spherical gaussian surface of 10.0 cm radius centred on the charge.
(a) If the radius of the gaussian surface were doubled, how much flux would pass through the surface?
(b) What is the value of the point charge?
Answer:
(a) The electric flux depenf only on the charge present in the gaussian surface. So electric flux passing through the gaussian surface. So electric flux passing through the gaussian surface of double the radius will be the same i.e.
Φ = -1.0 x 10³ Nm² C^-1 = -10³ Nm² C^-1

(b) since Φ = \(\frac{q}{\varepsilon_0}\)
∴ q = ε₀Φ
= 8.854 x 10^-12 x (-03)
= - 8.8 x 10^-9 C
= - 8.8 nC

Question 1.21.
A conducting shpere of radius 10 cm has an unknown charge. If the electric field 20 cm from the centre of the sphere is 1.5 x 10³ NC^-1 and points radially inward, what is the net charge on the sphere?
Answer:
Given E = -1.5 x 10³ NC^-1 [∵ E is directed inwards]
r = 20 cm = 0.2 m, q = ?
Since E = \(\frac{9 \times 10^9 \times q}{r^2}\)
∴ q = \(\frac{\mathrm{E} r^2}{9 \times 10^9}=-\frac{1.5 \times 10^5 \times 0.04}{9 \times 10^9}\)
= -6.67 C

Question 1.22.
A uniformly charged conducting sphere of 2.4 m diameter has a surface charge density of 80.0 µC m^-2
(a) Find the charge on the sphere.
(b) What is the total electric flux leaving the surface of the sphere?
Answer:
Given 
σ = 80.0 µCm^-2 = 80 x 10^-6 C m^-2
D = 2.4 m
or r = 1.2 m
(a) Charge on the sphere,
q = σ x 4πr²
or q = 80 x 10^-6 x 4 x 3.142 x (1.2)² = 1.45 x 10^-3 C
(b) Electric flux, Φ = \(\frac{q}{\varepsilon_0}\)
= \(\frac{1.45 \times 10^{-3}}{8.854 \times 10^{-12}}\) = 1.64 x 10⁸ NC^-1 m²

Question 1.23.
An infinite line charge produces a field of 9 x 10⁴ NC^-1 at a distance of 2 cm. Calculate the linear charge density.
Answer:
Given 
E = 9 x 10⁴ NC^-1 
r = 2 cm = 0.2 m
Since E = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{2 \lambda}{r}\)
or λ = \(\frac{4 \pi \varepsilon_0 \times \mathrm{E} \times r}{2}=\frac{9 \times 10^4 \times 0.02}{9 \times 10^9 \times 2}\) = 10^-7 C m^-1
= 0.1 x 10^-6 Cm^-1 = 0.10 µC m^-1

Question 1.24.
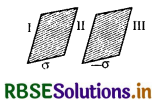
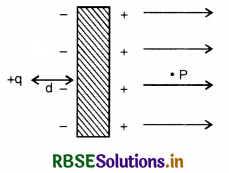
Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17.0 x 10^-22 Cm^-2.
What is \(\overrightarrow{\mathrm{E}}\) : (a) in the outer region of the first plate (b) in the outer region of the second plate, and (c) between the plates?
Answer:
Given ±σ = 17.0 x 10^-22 cm^-2 (See Fig.TBQ 1.24)
(a) In region I,
E = \(-\frac{-\sigma+\sigma}{2 \varepsilon_0}\) = 0
(b) In region II,
E = \(\frac{\sigma}{\varepsilon_0}=\frac{17 \times 10^{-22}}{8.854 \times 10^{-12}}\) = 1.92 x 10^-10 NC^-1
(c) In region III,
E = \(\frac{\sigma-\sigma}{2 \varepsilon_0}\) = 0

ADDITIONAL EXERCISES

Question 1.25.
An oil drop of 12 excess electrons is held stationary under a constant electric field of 2.55 x 10⁴ Vm^-1 in Millinkan's oil drop experment. The density of the oil is 1.26 g cm^-3. Estimate the radius of the drop.(g = 9.81 m s^-2; e = 1.60 x 10^-19 C).
Answer:
Under equilibrium,
qE = mg
neE = \(\frac{4}{3}\) πr³ ρg
r = \(\left(\frac{3 n e \mathrm{E}}{4 \pi \rho g}\right)^{1 / 3}\)

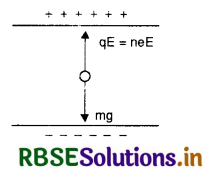
r = \(\left(\frac{3 \times 12 \times 1.6 \times 10^{-19} \times 2.55 \times 10^4}{4 \times \frac{22}{7} \times 1.26 \times 10^3 \times 9.8}\right)^{1 / 3}\)
= 9.82 x 10^-7 m
= 9.82 x 10^-4 mm.

Question 1.26.
Which of the follwoing figures cannot possibly rerpresent electrostatic field lines?

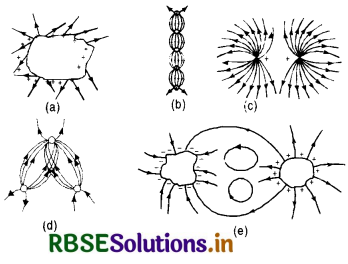
Answer:
Only (c) is right; the rest cannot represent electrostatic field lines.
(a) is werong because field lines must be normal to a conductor.
(b) is wrong because lines of force cannot start from a negative charge.
(d) is wrong because lines of force cannot interesect each other.
(e) is worng because electrostatic field lines cannot form closed loops.

Question 1.27.
In a certain region of space, electric field is along the z - direction throughout. The magnitude of electric field is, however, not constant but increase uniformly along the positive x - direction, at the rate of 10⁵ NC^-1 per metre. What are the force and torque experienced by a system having a total dipole moment equal to 10^-7 Cm in the negative z - directin?
Answer:
Given \(\frac{d \mathrm{E}}{d z}\) = 10⁵ NC^-1 per metre.
p = 10^-7 Cm
Electric dipole moment,
\(\overrightarrow{d p}\) = q x \(\overrightarrow{d z}\) = 10^-7 Cm along BA.
Let \overrightarrow{d E} is the increase in electric field in going from A to B.
Force on charge at A, \(\overrightarrow{\mathrm{F}_{\mathrm{A}}}\) = + q \(\overrightarrow{\mathrm{E}}\)
Force on charge at B, \(\overrightarrow{\mathrm{F}_{\mathrm{A}}}\) =+q \((\overrightarrow{\mathrm{E}} + d\overrightarrow{\mathrm{E}})\)
Net force, \(\overrightarrow{\mathrm{F}}\) = +q \(\overrightarrow{\mathrm{E}} - (\overrightarrow{\mathrm{E}} + d\overrightarrow{\mathrm{E}})\)
= q \(\overrightarrow{\mathrm{E}}\) - q \(\overrightarrow{\mathrm{E}}\) - q d\(\overrightarrow{\mathrm{E}}\)
or \(\overrightarrow{\mathrm{F}}\) = -q d\(\overrightarrow{\mathrm{E}}\)

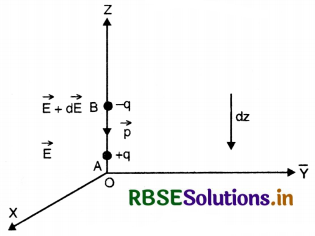
Magnitude of force, F = q\(\frac{d \mathrm{E}}{d z}\).dz
= (q dz) \(\frac{d \mathrm{E}}{d z}\) = 10^-7 x 10⁵
∴ F = 10^-2 N
Net torque, \(\vec{\tau}=\overrightarrow{r_1} \times \overrightarrow{\mathrm{F}_1}+\overrightarrow{r_2} \times \overrightarrow{\mathrm{F}_2}\)
where \(\overrightarrow{r_1}\) and \(\overrightarrow{r_2}\) are the position coordinates of two charges.
Now \(\overrightarrow{r_1},\overrightarrow{r_2}\) are in the same direction but \(\overrightarrow{F_1}\) and\( \overrightarrow{F_2}\) are in the opposite directions.
|\(\overrightarrow{r_1}\) x \(\overrightarrow{F_1}\)| = r₁ F₁ sin 0° = r₁ F₁ x 0 = 0
|\(\overrightarrow{r_2}\) x \(\overrightarrow{F_2}\)| = r₂ F₂ sin 180° = r₂ F₂ x 0 = 0
Hence torque τ is zero.

Question 1.28.
(a) A conductor A with a cavity as shown in figure TBQ 1.28 (a) is given a charge Q. Show that the entire charge must appear on the outer surface of the conductor.
(b) Another conductor B with charge q is inserted into the cavity keeping B insulated from A. Show that the total charge on the outside surface A is Q + q (Figure TBQ 1.28 b).
(c) A sensitive instrument is to be shifted from the strong electrostatic field in its environment. Suggest a possible way.

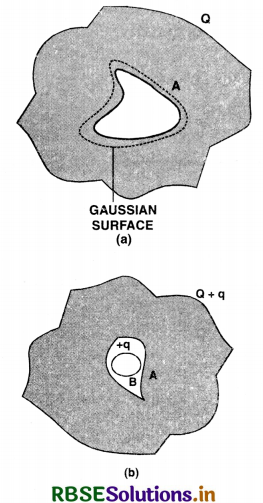
Answer:
(a) We know that the net field inside a charged conductor is zero i.e.
\(\overrightarrow{\mathrm{E}}\) = 0, inside.
Let us choose a gaussian surface lying wholly within the conductor and enclosing the cavity [Fig. TBQ 1.28 (a)].
According to Gauss’ law,
\(\oint \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\frac{q}{\varepsilon_0}=0\) (∵ \(\overrightarrow{\mathrm{E}}\) = 0, inside.)
∴ q = 0 i.e. charge inside the cavity is zero. Hence the entire charge Q on the conductor must appear on the outer surface of the conductor.
(b) The conductor B carrying a charge + q inserted in the cavity induces a charge - q on the metal surface of cavity and + q on the outside surface of the conductor A [Fig. TBQ 1.28 (b)]. As the outer surface of A originally had a charge Q, the total charge on it would become (Q + q).
(c) To shift a sensitive instrument from the strong electrostatic fields in its environment, enclose the instrument fully by a metallic surface.

Question 1.29.
A hollow charged conductor has a tiny hole cut into its surface. Show that the electric field in the hole is \(\frac{\sigma}{2 \varepsilon_0} \hat{n}\), where \(\hat{n}\) is the unit vector in the outward normal direction, and σ is the surface charge density near the hole.
Answer:
If the tiny hole in the hollow charged conductor were filled, then electric intensity E at a point P close to surface of conductor, according to Gauss’s law would be

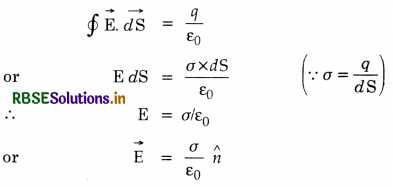
This field is superposition of field due to filled up hole plus the field due to rest of the charged conductor. The two fields inside the conductor are equal and opposite. That is why there is no electric field inside the conductor. But outside the conductor these fields are equal in magnitude and have the same direction.
∴ Field at P due to each = \(\frac{1}{2} \overrightarrow{\mathrm{E}}=\frac{\sigma}{2 \varepsilon_0} \cdot \hat{n}\)

Question 1.30.
Obtain the formula for the electric field due to a long thin wire of uniform linear charge density λ without using Gauss’s law.
Answer:
Suppose the point P is at a ⊥ distance OP = y from the infinite long-line charge. Consider a small charge element of length dx at a distance r from P.
Charge on the element, dq = λdx.
Electric intensity at P due to this charge element
dE = \(\frac{d q}{4 \pi \varepsilon_0 r^2}=\frac{\lambda d x}{4 \pi \varepsilon_0\left(y^2+x^2\right)}\) .......................(1)

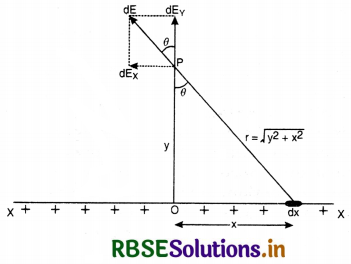
dE acts at ∠θ with OP produced.
Two rectangular components of dE are dE_x = - dE sin θ
(- sign for dE_x being along negative X - axis)
dE_y = dE cos θ
Corresponding to every charge element on the right of O, there is one on its left so that E_x due to both cancels out. Therefore, net field is along OP produced only.
∴ E_y = \(\int_{-\infty}^{+\infty} d E \cos \theta=2 \int_0^{\infty} d E \cos \theta\)
E_y = 2 ∫₀^∞\(\frac{\lambda d x}{4 \pi \varepsilon_0\left(y^2+x^2\right)}\) cos θ
From the figure, x = tan θ
∴ dx = y sec2θ dθ

E_y = \(\frac{\lambda}{2 \pi \varepsilon_0 y}\)

Question 1.31.
It is now believed that protons and neutrons (which constitute nuclei of ordinary matter) are themselves built out of more elementary units called quarks. A proton and a neutron consists of three quarks each. Two types of quarks, the so called 'up' quark (denoted by u) of charge + (2/3) e, and ‘down’ quark (denoted by d) of charge (-1/3) e, together with electrons build up ordinary matter (quarks of other types have also been found which give rise to different unusual varieties of matter.) Suggest a possible quark composition of a proton and neutron.
Answer:
Charge of u = + (2/3) e
Charge of d = (-1/3) e.
A proton and a neutron consists of three quarks each.
Quark composition of a proton is
u + d + d =\( \frac{2}{3}\) e+\(\frac{2}{3}\) e - \(\frac{1}{3}\) e = +e
Quark composition of a neutron is
u + u + d = \(\frac{2}{3}\) e - \(\frac{1}{3}\) e - \(\frac{1}{3}\) e = 0

Question 1.32.
(a) Consider an arbitrary electrostatic field configuration. A small test charge is placed at the null point (i.e. where \(\overrightarrow{\mathrm{E}}\) = 0) of the configuration. Show that the equilibrium of the test charge is necessarily unstable.
(h) Verify this result for the simple configuration of two charges of the same magnitude and sign placed a certain distance apart.
Answer:
(a) Let the equilibrium be stable, so on slightly displacing the test charge, we find that the charge will experience a restoring force towards the null point i.e., all field lines near the null point should be directed inwards towards the null - point So there is a net inward flux of electric field through a closed surface around the null point. But by Gauss’s law, the flux of electric field through a surface, not enclosing any charge, must be zero. Hence the equilibrium cannot be stable.

(b) For a system consisting of two charges of the same magnitude and sign, the null point lies at the mid - point of the line joining the two charges. If the test charge is slightly displaced along the line, there is restoring force. But if the test charge is displaced normal to the line, the test charge will go away from the null point. So the equilibrium is unstable because the stability of equilibrium requires restoring force in all directions.

Question 1.33.
A particle of mass m and charge (-q) enters the region between the two charged plates initially moving along x - axis with speed v_x (like particle in Fig. TBQ 1.33). The length of plate is L and a uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is qEL²i(2mvx²).
Answer:
The distance travelled by the charge along x-axis
L = v_xt
t = \(\frac{\mathrm{L}}{v_x}\) ...................(i)

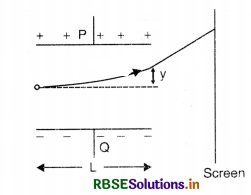
Force acting on the charge q is
F = qE
or ma = qE
or a = \(\frac{q \mathrm{E}}{m}\) ..................(ii)
The vertical deflection of the particle at the far edge
y = ut + \(\frac{1}{2}\) at²
= 0 + \(\frac{1}{2}\) at²
Using equations (i) and (ii), we get
y = \(\frac{q \mathrm{EL}^2}{2 m v_x^2}\) ...................(iii)

Question 1.34.
Suppose that the particle in Exercise 1.33 is an electron projected with velocity v_x = 2.0 x 10⁶ m s^-1. If E between the plates separated by 0.5 cm is 9.1 x 10² NC^-1, where will the electron strike the upper plate? (|e| = 1.6 x 10^-19 C, m_e = 9.1 x 10^-31 kg) 
Answer:
Since y = \(\frac{q \mathrm{EL}^2}{2 m v_x^2}\)
So \(\frac{0 \cdot 5 \times 10^{-2}}{2}=\frac{1 \cdot 6 \times 10^{-19} \times 9 \cdot 1 \times 10^2 \times \mathrm{L}^2}{2 \times 9 \cdot 1 \times 10^{-31} \times\left(2 \times 10^6\right)^2}\)
or L² = \(\frac{2}{1.6}\) x 10^-4
or L = 1.12 x 10^-2 = 1.12 cm
Hence we find that an electron will strike the upper plate, if length of the plate is 1.12 cm.

SELECTED EXEMPLAR PROBLEMS

MCQ I (with one correct option)

Question 1.1.
In Fig. EP 1.1, two positive charges q₂ and q₃ fixed along the y - axis, exert a net electric force in the + x direction on a charge q₁ fixed along the x - axis. If a positive charge Q is added at (x, 0), the force on q₁

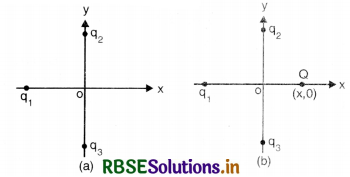
(a) shall increase along the positive x-axis.
(b) shall decrease along the positive x-axis.
(c) shall point along the negative x-axis.
(d) shall increase but the direction changes because of the intersection of Q with q₂ and q₃.
Answer:
(a) Here charge q₁ is negative. Charge Q will attract q₁ along + x direction.

Question 1.2.
A point positive charge is brought near an isolated conducting sphere (Fig. EP 1.2). The electric field is best given by-

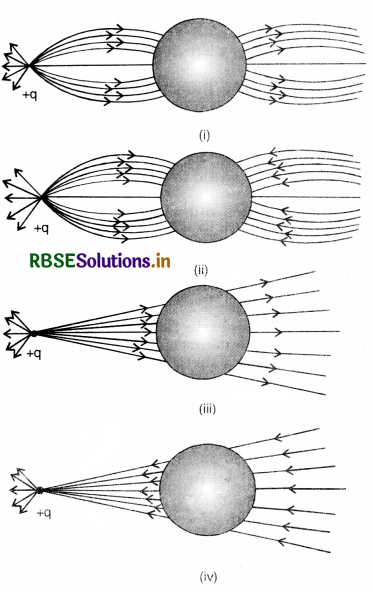
(a) Fig. EP 1.2 (i)
(b) Fig. EP 1.2 (ii)
(c) Fig. EP 1.2 (iii)
(d) Fig. EP 1.2 (iv)
Answer:
(a) Here +q charge induces -ve charge on the left side of the sphere and +ve charge on the right side of the sphere.

Question 1.3.
The Electric flux through the surface 
(a) in Fig. EP 1.3 (iv) is the largest.
(b) in Fig. EP 1.3 (iii) is the least.
(c) in Fig EP 1.3 (ii) is same as Fig. EP 1.3 (iii) but is smaller than Fig. EP 1.3 (iv)
(d) is the same for all the figures.

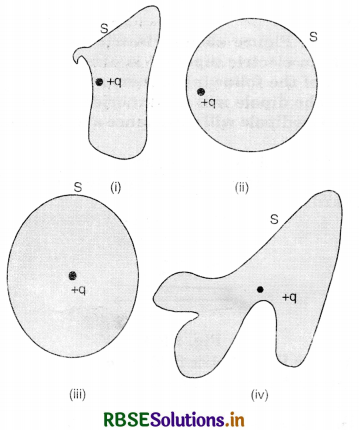
Answer:
(d) because, the flux Φ = \(\frac{q}{\varepsilon_0}\) is independent of the shape of the gaussian surface.

Question 1.4.
Five charges q₁, q₂, q₃, q₄ and q₅ are fixed at their positions as shown in Fig. EP 1.4 S is a gaussian surface. The Gaus' law is given by in a gaussian surface. The Gauss' law is given by 
\(\oint_{\mathrm{s}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\frac{q}{\varepsilon_0}\)

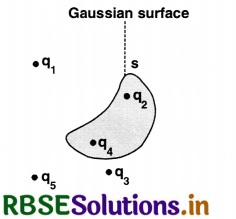
Which of the following statements is correct?
(a) E on the LHS of the above equation will have a contribution from q₁, q₅ and q₃ while q on the RHS will have a contribution from q₂ and q₄ only.
(b) E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q₂ and q₄ only.
(c) E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q₁, q₃ and q₅ only.
(d) Both E on the LHS and q on the RHS will have contributions from q₂ and q₄ only.
Answer:
(b) E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q₂ and q₄ only.

Question 1.5.
Figure shows electric field lines in which an electric dipole P is placed as shown. Which of the following statements is correct?
(a) The dipole will not experience any force.
(b) The dipole will experience a force towards right.
(c) The dipole will experience a force towards left.
(d) The dipole will experience a force upwards.

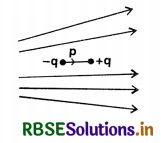
Answer:
(c) Here electric field at -q is more than the electric field at +q, so force on -q is more than force on +q.

Question 1.6.
A point charge +q, is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of the plane is
(a) directed perpendicular to the plane and away from the plane.
(b) directed perpendicular to the plane but towards the plane.
(c) directed radially away from the point charge.
(d) directed radially towards the point charge.
Answer:
(a) Because

Question 1.7.
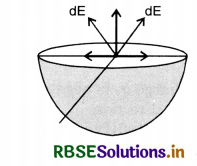
A hemisphere is uniformly charged positively. The electric field at a point on a diameter away from the centre is directed
(a) perpendicular to the diameter
(b) parallel to the diameter
(c) at an angle tilted towards the diameter
(d) at an angle tilted away from the diameter.
Answer:
(a) Because the components of electric field parallel to the diameter cancels out as shown in Fig. EP 1.7.

MCQ II (with more than one correct options)

Question 1.8.
If \(\oint_{\mathrm{s}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=0\) over a surface, then 
(a) the electric field inside the surface and on it is zero.
(b) the electric field inside the surface is necessarily uniform.
(c) the number of flux lines entering the surface must be equal to the number of flux lines leaving it.
(d) all charges must necessarily be outside the surface.
Answer:
(c), (d), \(\oint_{\mathrm{s}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}\) → 0 means net flux over the surface is zero.

Question 1.9. 
The Electric field at a point is
(a) always continuous.
(b) continuous if there is no charge at the point.
(c) discontinuous only if there is a negative charge at that point.
(d) discontinuous if there is a charge at that point.
Answer:
(b), (d), because electric field is continuous only in charge free region.

Question 1.10.
If there were only one type of charge in the universe, then
(a) \(\oint_{\mathrm{S}} \overrightarrow{\mathbf{E}} \cdot d \overrightarrow{\mathrm{S}}\) ≠ 0 on any surface.
(b) \(\oint_{\mathrm{S}} \overrightarrow{\mathbf{E}} \cdot d \overrightarrow{\mathrm{S}}\) = 0 if the charge is outside the surface.
(c) \(\oint_{\mathrm{S}} \overrightarrow{\mathbf{E}} \cdot d \overrightarrow{\mathrm{S}}\) could not be defiened.
(d) \(\oint_{\mathrm{S}} \overrightarrow{\mathbf{E}} \cdot d \overrightarrow{\mathrm{S}} = \frac{q}{\varepsilon_0}\) if charges of magnitude q were inside the surface.
Answer:
(b), (d) See Gauss' law.

Question 1.11
Consider a region inside which there are various types of charges but the total charge is zero. At points outside the region
(a) the electric field is necessarily zero.
(b) the electric field is due to the dipole moment of the charge distribution only.
(c) the dominant electric field is ∝\(\frac{1}{r^3}\), for large r where r is the distance from the origin in this region.
(d) the work done to move a charged particle along a closed path, away from the region, will be zero.
Answer:
(c), (d),  because electric field due to dipole having net charge zero is E ∝\(\frac{1}{r^3}\) and electric field is conservative in nature.

Question 1.12.
Refer to the arrangement of charges in Fig. EP 1.12 and a gaussian surface of radius R with Q at the centre. Then

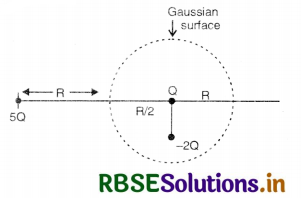
(a) total flux through the surface of the sphere is \(\frac{-\mathrm{Q}}{\varepsilon_0}\).
(b) field on the surface of the shpere is \(\frac{-Q}{4 \pi \varepsilon_0 R^2}\).
(c) flux through the surface of shpere due to 5Q is zero.
(d) field on the surface of sphere due to -2Q is same everywhere.
Answer:
(a), (c) because Φ = \(\frac{\mathrm{Q}_{\text {net }}}{\varepsilon_0}\).

Question 1.13.
A positive charge Q is uniformly distributed along a circular ring of radius R. A small test charge q is placed at the centre of the ring (Fig. EP 1.13). Then

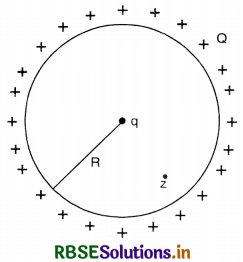
(a) If q > 0 and is displaced away from the centre in the plane of the ring. It will be pushed back towards the centre.
(b) If q < 0 and is displaced away from the centre in the plane of the ring. It will never return to the centre and will continue moving till it hits the ring.
(c) If q < 0, it will perform SHM for small displacement along the axis.
(d) q at the centre of the ring is in an unstable equilibrium within the plane of the ring for q > 0.
Answer:
(a), (b), (c) because the electric field E = 0 at the centre of the ring.

Very Short Answer Type Questions

Question 1.14.
An arbitrary surface encloses a dipole. What is the electric flux through this surface?
Answer:
Φ = \(\frac{q_{\text {net }}}{\varepsilon_0}=\frac{0}{\varepsilon_0}\) = zero.

Question 1.15.
A metallic spherical shell has an inner radius R₁ and outer radius R₂. A charge Q is placed at the centre of the spherical cavity. What will be surface charge density on (i) the inner surface, and (ii) the outer surface?
Answer:
-Q charge will induce on the inner side and +Q charge will induce on the outer side.
So σ on the inner side = \(\frac{-\mathrm{Q}}{4 \pi \mathrm{R}_1^2}\)
And σ on the outer side = \(\frac{\mathrm{Q}}{4 \pi \mathrm{R}_2^2}\)

Question 1.16.
The dimensions of an atom are of the order of an angstrom. Thus there must be large electric fields betweem the protons and electrons. Why, then is the electrostatic field inside a conductor zero?
Answer:
A conductor is neutral, so the electrostatic field (which is due to charge) is zero inside the conductor.

Question 1.17.
If the total charge enclosed by a surface is zero, does it imply that the electric field everywher on the surface is zero? Conversely, if the elctric field everywhere on a surface is zero, does it imply that net charge iside is zero.
Answer:
No, the field may be normal. The converse is true.

Question 1.18.
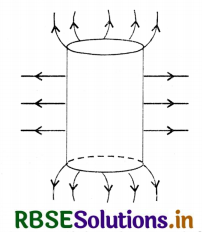
Sketch the electric field lines for a uniformly charged hollow cylinder shown in Fig. EP 1.18(a)

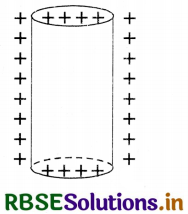
Answer:
Electric lines of force are shown in Fig. EP 1.18 (b)

Question 1.19.
What will be the total flux through the faces of the cube (Fig. EP 1.19) with side of length a if a charge q is palced at

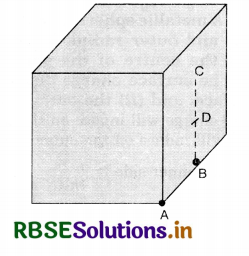
(a) A: a corner of the cube
(b) B: mid-point of an edge of the cube.
(c) C: centre of a face of the cube.
(d) D: mid-point of B and C.
Answer:
(a) Φ = \(\frac{q / 8}{\varepsilon_0}=\frac{q}{8 \varepsilon_0}\) [∵ q is shared by eight cubes]
(b) Φ = \(\frac{q / 4}{\varepsilon_0}=\frac{q}{4 \varepsilon_0}\) [∵ q is shared by four cubes]
(c) Φ = \(\frac{q / 2}{\varepsilon_0}=\frac{q}{2 \varepsilon_0}\) [∵ Centre of face is shared by two cubes]
(d) Φ = \(\frac{q / 2}{\varepsilon_0}=\frac{q}{2 \varepsilon_0}\) [∵ D is shared by two cubes]

Short Answer Type Questions

Question 1.20.
A paisa con is made up of Al-Mg alloy and weighs 0.75 g. It has a square shape and its diagonal measures 17 mm. It is electrically neutral and contains equal amounts of positive and negative charges.
Treating the paisa coins made up of only Al, find the magnitude of equal number of positive and negative charges. What conclusion do you draw from this magnitude?
Answer:
Here m = mass of Al paisa = 0.75 g
M = molecular mass of Al = 26.9815 g
N_A = 6.023 x 10²³ atoms, = Z_Al = 13
Number of atoms of Al in the coin
n = N_A \(\frac{m}{\mathrm{M}}\)
= \(\frac{6.023 \times 10^{23} \times 0.75}{26.9815}\) = 1.67 x 10²² atoms
Since q = nZe
= 1.67 x 10²² x 13 x 1.6 x 10^-19
= 3.48 x 10⁴ C = 34.8 kC
Thus coin of Al contains ± 34.8 kC
This is very large charge. So we see that ordinary neutral matter contains enormous amount of ± charges.

Question 1.21.
Consider a coin of Question 1.20. It is electrically neutral and contains equal amounts of positive and negative charge of magnitude 34.8 kC. Suppose that these equal charges were concentrated in two point charges seprated by
(i) 1 cm [~ \(\frac{1}{2}\) x diagonal of the one paisa coin]
(ii) 100 m (~ length of a long building), and 
(iii) 106 m (radius of the earth). Find the force on each such point charge in each of the three cases. What do you conclude from these results?
Answer:

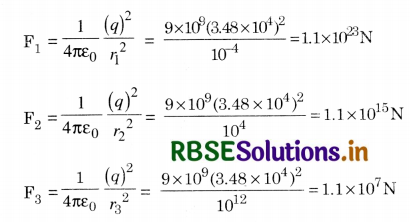
Question 1.23.
Two charges q and -3q are placed fixed on x-axis separated by distance 'd'. Where should a third charge 2q be placed such that it will not experience any force?
Answer:
2q must be placed such that
Force on 2q due to q = Force on 2q due to -3q

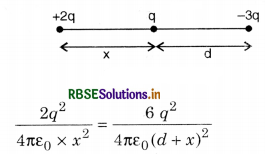
or (d + x)² = 3x²
or 2x² - 2d x - d² = 0
or x = \(\frac{2 d \pm \sqrt{4 d^2+8 d^2}}{2}=\frac{d \pm \sqrt{3} d}{2}=\frac{d}{2}(1+\sqrt{3} d)\)
(-ve sign is neglected as -ve sign between q and -3q is unacceptable).

Question 1.24.
Fig. EP 1.24 shows the electric field lines around three point charges A, B and C.

(a) Which charges are positive?
(b) Which charge has the largest magnitude? Why?
(c) In which region or rerions of the picture could the elctric field be zero? Justify your answer.
(i) near A, (ii) near B, (iii) near C, (iv) nowhere.
Answer:
(a) charegs A and C are positive as electric lines of force emanate from them.
(b) As macimum number of lines are associated with charge C, so charge C has the largest magnitude. 
(c) Electric field is zero in between two like charges and near to the charge closer to the charge with smaller magnitude, so electric field is zero near A.

Long Answer Type Questions

Question 1.26.
In 1959 Lyttleton and Bondi suggested that the expansion of the Universe could be explained if matter carried a net charge. Suppose that the Universe is made up of hydrogen atoms with a number density N, which is maintained a constant. Let the charge on the proton be : e_p = -(1 + y)e, where e is the electronic charge.
(a) Find the critical value of y such that expansion may start.
(b) Show that the velocity of expansion is proportional to the distance from the centre.
Answer:
(a) Let radius of universe = R and universe is made up of hydrogen atoms having constant number density.
∴ Charge on each hydrogen atom 
e_H = -(1 + y) e + e = -ye = |ye|
The expansion starts if the coulomb repuslion on a hydrogen atom at R is more than gravitational force of attaction.
From Gauss's Theorem \(\oint \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\frac{q}{\varepsilon_0}\)
If \(\overrightarrow{\mathrm{E}}(R)\) is the electric field at R, then
4πR² \(\overrightarrow{\mathrm{E}}(R) = \frac{4}{3} \frac{\pi R^3}{\varepsilon_0} \mathrm{~N} \mid \text { ye } \mid\)
or \(\overrightarrow{\mathrm{E}}(R) = \frac{1}{3} \frac{\mathrm{N}|y e|}{\varepsilon_0} \mathrm{R}(\hat{\mathrm{R}})\) .................(i)
If G_R is the gravitational field at R, then
-4πR² G_R = 4πg m_p \(\left(\frac{4}{3} \pi R^3\right)\) N [m_p is mass of proton]
or G_R = -\(\frac{4}{3} \pi \mathrm{G} m_p \mathrm{NR}\)
or \(\overrightarrow{\mathrm{G}}_{\mathrm{R}}(R) = -\frac{4}{3} \pi \mathrm{G} m_p \mathrm{NR}\) ........................(ii)
Coulomb force on a hydrogen atom at R is given by multiplying eqn. (i) by ye
ye \(\overrightarrow{\mathrm{E}}\) = \(\frac{1}{3} \frac{\mathrm{N} y^2 e^2}{\varepsilon_0} \mathrm{R}(\hat{r})\) .........................(iii)
The gravitational force on this atom is given by multiplying equation (ii) by m_p, so we get
m_p\( \overrightarrow{\mathrm{G}}_{\mathrm{R}} = -\frac{4}{3} \pi \mathrm{G} m_p^2 \mathrm{NR}(\hat{r})\)
The net force on the atom is 
\(\overrightarrow{\mathrm{F}} = \left[\frac{1}{3} \frac{\mathrm{N} y^2 e^2}{\varepsilon_0} \mathrm{R}-\frac{4}{3} \pi \mathrm{G} m_p^2 \mathrm{NR}\right]^{\wedge}\)
The critical value is when 
\(\frac{1}{3} \frac{\mathrm{N} y_c^2 e^2}{\varepsilon_0} \mathrm{R}=\frac{4}{3} \pi \mathrm{G} m_p^2 \mathrm{NR}\)
or y_c² = 4πε₀G \(\frac{m_p^2}{e^2}\)
= \(\frac{1}{9 \times 10^9} \times \frac{7 \times 10^{-11} \times(1.8)^2 \times 10^6 \times 81 \times 10^{-62}}{(1.6)^2 \times 10^{-38}}\)
= 63 x 10^-38
or y_c = 8 x 10^-19 ≃ 10^-18 ...................(iv)
(b) The hydrogen atom experiences an acceleration due to the net force and is given by

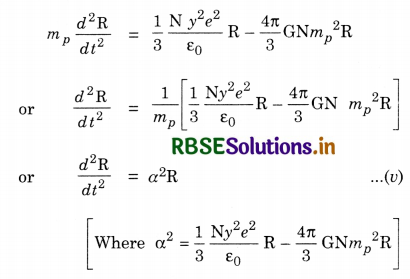
The solution of eq.(v) is the form 
R = A e^αt + Be^-αt
As we are seeking an expansion, B = 0
∴ R = A e^αt
or R = α A e^αt = α R
or V ∝ R i.e. velocity is proportional to the distance from the centre.

Question 1.28.
Two fixed, identical conducting plates (α & ß), each of surface area S are charged to -Q and q, respectively, where Q > q > 0. A third identical plate (γ), free to move is located on the other side of the plate with charge q at a distance d (Fig. EP 1.28 (a)). The third plate is released and collides with the plate ß. Assume the collision is elastic and the time of collision is sufficent to redistribute charge amongst ß & γ.

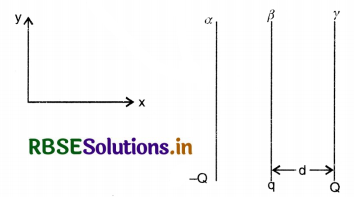
(a) Find the electric field acting on the plate γ before collision.
(b) Find the charges on ß and γ after the collision.
(c) Find the velocity of the plate γ after the collision and at a distance d from the plate ß.
Answer:
(a) Electric field at γ due to plate α,
E₁ = \(-\frac{\sigma}{2 \varepsilon_0}=-\frac{\mathrm{Q}}{2 \varepsilon_0 \mathrm{~S}}\)
Electric field at γ due to plate ß,
E₂ = \(\frac{\sigma}{2 \varepsilon_0}=\frac{q}{2 \varepsilon_0 \mathrm{~S}_0}\)
∴ Net electric field,
E = E₁ + E₂ = \(\frac{q-Q}{2 \varepsilon_0 S}\) towards right.

(b) During the collision the plates ß and γ are in contact hence are at the same potential. Let q₁ be charge on ß and q₂ be charge on γ.
Consider a point O as shown in the figure EP 1.28(b).
Electric field at O due to α,

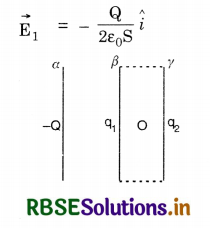
Electric field at O due to ß,
\(\overrightarrow{\mathrm{E}}_2=\frac{q_1}{2 \varepsilon_0 \mathrm{~S}} \hat{i}\)
Electric field at O due to γ,

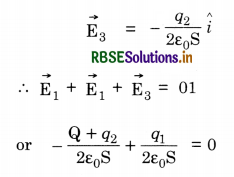
or q₁ - q₂ = Q ......................(i)
Also q₁ + q₂ = Q + q ..........................(ii)
Adding and subtracting eqn.(i) and ε₁ (ii), we get 
q₁ = Q +\( \frac{q}{2}\) and q₂ = \(\frac{q}{2}\)
Thus the charge on ß and γ are Q + \(\frac{q}{2}\) and \(\frac{q}{2}\) respectively.

(c) let v be the velocity of plate γ at a distance d after collision.
Electric field at γ before collision
\(\overrightarrow{\mathrm{E}}_1=\frac{\mathrm{Q}-q}{2 \varepsilon_0 \mathrm{~S}} \hat{i}\)
Electric field at γ after collision
\(\overrightarrow{\mathrm{E}}_2=-\frac{\mathrm{Q}}{2 \varepsilon_0 \mathrm{~S}} \hat{i}+\frac{\left(\mathrm{Q}+\frac{q}{2}\right)}{2 \varepsilon_0 \mathrm{~S}} \hat{i}=\frac{\frac{q}{2}}{2 \varepsilon_0 \mathrm{~S}} \hat{i}\)
The work done when plate γ is released till it  collides with plate ß.
W₁ = F₁d = (E₁Q) d = \(\frac{(\mathrm{Q}-q)}{2 \varepsilon_0 \mathrm{~S}}\) Qd
The work done after the collision till it reaches 'd'
W₂ = F₂d = \(\left(\mathrm{E}_2 \frac{q}{2}\right) d=\frac{(q / 2)^2}{2 \varepsilon_0 \mathrm{~S}} \)d
Total work done,
W = W₁ + W₂ = \(\frac{1}{2 \varepsilon_0 S}\left[(\mathrm{Q}-q) \mathrm{Q}-\left(\frac{q}{2}\right)^2\right]\) d
or W = \(\frac{d}{2 \varepsilon_0 \mathrm{~S}}(\mathrm{Q}-q / 2)^2 d\)
And work done = gain in K.E.
So \(\frac{d}{2 \varepsilon_0 \mathrm{~S}}\left(\mathrm{Q}-\frac{q}{2}\right)^2 d=\frac{1}{2} m v^2\) [m is the mass of the plate γ]
or v = \(\left(Q-\frac{q}{2}\right)\left(\frac{d}{\mathrm{M} \varepsilon_0 \mathrm{~S}}\right)^{1 / 2}\)

Question 1.29.
There is another useful system of units, besides the SI/MKS A system, called the cgs (centimetre - gram - second) system. In this system Coulomb's law is given by
\(\overrightarrow{\mathrm{F}}=\frac{Q q}{r^2} \hat{r}\)
where the distance r is measured in cm (= 10^-2 m), F in dynes (= 10^-5 N) and the charges in electrosatic units (es units), where 1 es unit of charge =\( \frac{1}{[3]}\) x 10^-9 C.
The number [3] actually arises from the speed of light in vacuum which is now taken to be exactly given by c = 2.99792458 x 10⁸ m/s. An approximate value of c then is c = [3] x 10⁸ m/s.
(i) Show that the Coulomb law in cgs units yields 
1 esu of charge =  (dyne)^1/2 cm.
Obtain the dimensions of units of charge in terms of mass M, length L and time T. Show that it is given in terms of fractional powers of M and L.
(ii) Write 1 esu of charge = x C, where x is a dimensionless number. Showe that this gives 

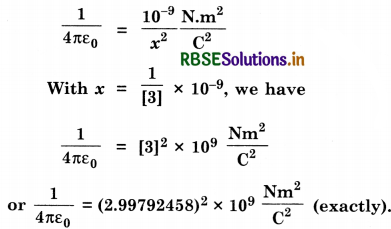
Answer:
(i) We know that in cgs system of units 
F = \(\frac{Q q}{r^2}\) 1 dyne = \(\frac{(1 \text { esu of charge })^2}{(1 \mathrm{~cm})^2}\)
∴ (1 esu of charge) = \(\sqrt{1 \text { dyne }}\). 1cm
= [F]\(\frac{1}{2}\) [L]
or 1 esu of charge = [MLT^-2]^1/2 (L)
= [M^1/2 L^3/2 T^-1]
Hence charge in cgs units is expressed as fractional power \(\left(\frac{1}{2}\right)\) of M, \(\left(\frac{3}{2}\right)\) of L and (-1) of T.

(ii) We know that 1 dyne = 10^-5 N and here q = xC

Question 1.31.
Total charge -Q is uniformly spread along lenght of a ring of radius R. A small test charge +q of mass m is kept at the centre of the ring and is given a gentle push along the axis of the ring.
(a) Show that the particle executes a simple harmonic oscillation.
(b) Obtain its time period.
Answer:
(a) Since the charge -Q is distributed along the length of the ring of radius R.
∴ Charge per unit lenght = \(\frac{-\mathrm{Q}}{2 \pi \mathrm{R}}\)

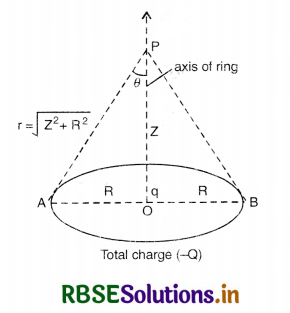
Force on q due to this charge element at A and B
F_A+B = \(\left[\frac{1}{4 \pi \varepsilon_0}\left(\frac{-\mathrm{Q}}{2 \pi \mathrm{R}}\right) q \cdot \frac{1}{r^2} \cos \theta\right]\)
= \(\frac{-\mathrm{Qq}}{4 \pi \varepsilon_0 \pi \mathrm{R}} \cdot \frac{1}{\left(\mathrm{Z}^2+\mathrm{R}^2\right)} \cdot \frac{\mathrm{Z}}{\left(\mathrm{Z}^2+\mathrm{R}^2\right)^{1 / 2}}\)
Total force on q due to whole ring will be
F = (F_A+B)πR
or F = \(\frac{-\mathrm{Q} q}{4 \pi \varepsilon_0} \frac{\mathrm{Z}}{\left(\mathrm{Z}^2+\mathrm{R}^2\right)^{3 / 2}}\)
For Z = R
F = \(\frac{-Q q}{4 \pi \varepsilon_0 R^3}\) Z ......................(i)
or F = -k Z [where k = \(\frac{\mathrm{Q} q}{4 \pi \varepsilon_0 \mathrm{R}^3}\)]
or F ∝ -Z
Hence the motion of charge is SHM.
(b) Since ω = \(\sqrt{\frac{k}{m}}\)
Uding eq.(i), we get 
ω = \(\sqrt{\frac{\mathrm{Q} q}{4 \pi \varepsilon_0 \mathrm{R}^3 m}}\)
∴ T = \(\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{4 \pi \varepsilon_0 m \mathrm{R}^3}{\mathrm{Q}}}\)