RBSE Solutions for Class 11 Maths Chapter 3 त्रिकोणमितीय फलन Ex 3.1

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 3 त्रिकोणमितीय फलन Ex 3.1 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 3 त्रिकोणमितीय फलन Ex 3.1

प्रश्न 1.
निम्नलिखित डिग्री माप के संगत रेडियन माप ज्ञात कीजिए
(i) 25°
(iii) 240°
(ii) - 47°30'
(iv) 520°
हल:
हम जानते हैं कि 180° = π रेडियन
1° = \(\frac{\pi}{180}\) रेडियन

(i) 25° = 25 × \(\frac{\pi}{180}=\frac{5 \pi}{36}\) रेडियन

(ii) - 47°30′ ∵ 60′ = 1°

(iii) 180° = π रेडियन
240° = 240 × \(\frac{\pi}{180}\) रेडियन = \(\frac{4 \pi}{180}\) रेडियन

(iv) 180° = π रेडियन
520° = 520 × \(\frac{\pi}{180}\) रेडियन = \(\frac{26 \pi}{180}\) रेडियन

प्रश्न 2.
निम्नलिखित रेडियन माप के संगत डिग्री माप ज्ञात कीजिए
(π = \(\frac{22}{7}\) का प्रयोग करें)
(i) \(\frac{11}{16}\)
(ii) - 4
(iii) \(\frac{5 \pi}{3}\)
(iv) \(\frac{7 \pi}{6}\)
हल:
हम जानते हैं कि रेडियन Π

प्रश्न 3.
एक पहिया एक मिनट में 360 परिक्रमण करता है तो एक सेकण्ड में कितने रेडियन माप का कोण बनाएगा?
हल:
1 परिक्रमण में पहिये द्वारा बनाया गया कोण = 2π रेडियन
∴ 360 परिक्रमण में पहिये द्वारा बनाया गया कोण = 360 × 2 रेडियन
अतः 1 मिनट या 60 सेकण्ड में बनाया गया कोण = 360 × 2 रेडियन
∴ 1 सेकण्ड में बनाया गया कोण = \(\frac{360 \times 2 \pi}{60}\)
= 12π रेडियन

प्रश्न 4.
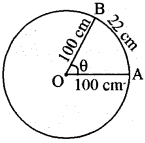
एक वृत्त, जिसकी त्रिज्या 100 सेमी. है, को 22 सेमी. लम्बाई की चाप वृत्त के केन्द्र पर कितने डिग्री माप का कोण बनाएगी ।
(π = \(\frac{22}{7}\) का प्रयोग कीजिए ।)
हल:
हम जानते हैं कि 1 = rθ
यहाँ r = 100 cm, l = 22 cm
∴ 22 = 100 × θ

प्रश्न 5.
एक वृत्त, जिसका व्यास 40 सेमी. है, की एक जीवा 20 सेमी. लम्बाई की है तो इसके संगत छोटे चाप की लम्बाई ज्ञात कीजिए।
हल:
माना कि बिन्दु O वृत्त के व्यास का केन्द्र बिन्दु है । हम जानते हैं कि प्रश्नानुसार वृत्त का व्यास 40 सेमी. है अतः त्रिज्या (r) = 20 cm.
ΔOBC एक समबाहु त्रिभुज है

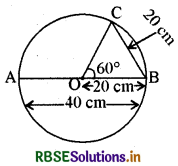
∴ ∠BOC = 60°
∴ θ = \(\frac{60 \times \pi}{180}\) रेडियन = \(\frac{\pi}{3}\) रेडियन
हम जानते हैं कि l = rθ
या l = 20 × \(\frac{\pi}{3}\)
= \(\frac{20\pi}{3}\) cm
= \(\frac{20}{3} \times \frac{22}{7}=\frac{440}{21}\) cm
= 20.95 cm.
अतः वृत्त की जीवा के संगत चाप की लम्बाई
= \(\frac{20\pi}{3}\)cm. या 20.95 cm

प्रश्न 6.
यदि दो वृत्तों के समान लम्बाई वाले चाप अपने केन्द्रों पर क्रमश: 60° तथा 75° के कोण बनाते हों, तो उनकी त्रिज्याओं का अनुपात ज्ञात कीजिए ।
हल:
माना कि चाप की लम्बाई l है ।
चाप द्वारा केन्द्र पर बना कोण = 60°
q₁ = \(\frac{\pi}{3}\) रेडियन

माना कि इस वृत्त की त्रिज्या

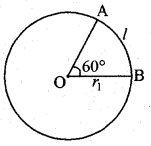
∴ l = r₁θ₁
= r₁\(\frac{\pi}{3}\)
∴ r₁ = \(\frac{3 l}{\pi}\) .......(i)

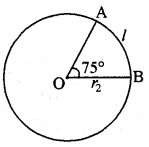
इसी प्रकार माना कि दूसरे वृत्त की त्रिज्या r₂ है
तथा चाप की लम्बाई l है । चूँकि दिया गया है कि समान लम्बाई के चाप हैं ।
चाप द्वारा केन्द्र पर बना कोण = 75° रेडियन

प्रश्न 7.
75 सेमी. लम्बाई वाले एक दोलायमान दोलक का एक सिरे से दूसरे सिरे तक दोलन करने से जो कोण बनता है, उसका माप रेडियन में ज्ञात कीजिए, जबकि उसके नोक द्वारा बनाए गए चाप की लम्बाई निम्नलिखित हैं-
(i) 10 सेमी.
(ii) 15 सेमी.
(iii) 21 सेमी.
हल:
(i) प्रश्नानुसार
r = 75 सेमी.
l = 10 सेमी.
θ = ?

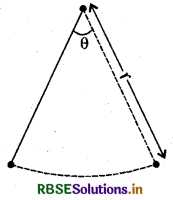
∵ हम जानते हैं कि θ = \(\frac{l}{r}\)
= \(\frac{10}{75}\) रेडियन = \(\frac{2}{15}\) रेडियन

(ii) यहाँ r = 75 सेमी., l = 15 सेमी., θ = ?
∴ θ = \(\frac{l}{r}=\frac{15}{75}\) रेडियन = \(\frac{1}{5}\) रेडियन

(iii) यहाँ r = 75 सेमी., l = 21 सेमी., θ = ?
∴ θ = \(\frac{l}{r}=\frac{15}{75}\) रेडियन = \(\frac{7}{25}\) रेडियन