RBSE Solutions for Class 11 Maths Chapter 2 संबंध एवं फलन विविध प्रश्नावली

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 2 संबंध एवं फलन Ex विविध प्रश्नावली Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 2 संबंध एवं फलन Ex विविध प्रश्नावली

प्रश्न 1.
सम्बन्ध f,

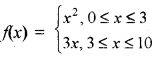
द्वारा परिभाषित है ।
सम्बन्ध g,

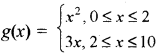
द्वारा परिभाषित है ।
दर्शाइए कि क्यों f एक फलन है और g फलन नहीं है ।
हल:
सम्बन्ध f,

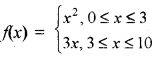
द्वारा परिभाषित है ।
f(0) = 0, f(1) = 1, f(2) = 4, f(3) = 9 f(4) = 12, f(5) = 15, f(6) = 18, f(7) = 21 f(8) = 24, f(9) = 27, f(10) = 30
⇒ f(x) = {(0, 0), (1, 1), (2, 4), (3, 9)} ∪ {(3, 9), (4, 12), (5, 15), (6, 18), (7, 21), (8, 24), (9, 27), (10, 30)}
⇒ f(x) = {(0, 0), (1, 1), (2, 4), (3, 9), (4, 12), (5, 15), (6, 18), (7, 21), (8, 24), (9, 27), (10, 30)}
स्पष्ट है कि f एक फलन है क्योंकि प्रान्त का प्रत्येक अवयव सहप्रान्त के केवल और केवल एक अवयव से सम्बन्धित है । इसी प्रकार
सम्बन्ध g,

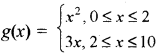
द्वारा परिभाषित है ।
g(0) = 0, g(1) = 1, g(2) = 4, g(2) = 6
स्पष्ट है कि g फलन नहीं है क्योंकि (2, 4) तथा (2,6) में प्रथम घटक 2 समान अवयव है।

प्रश्न 2.
यदि f(x) = x², तो \(\frac{f(1.1)-f(1)}{(1.1-1)}\) ज्ञात कीजिए ।
हल:
प्रश्नानुसार f (x) = x²
∴ f(1.1) = (1.1)² = 1.21
तथा f(1) = 1² = 1
∴ \(\frac{f(1.1)-f(1)}{1.1-1}=\frac{1.21-1}{1.1-1}=\frac{0.21}{0.1}\) = 2.1

प्रश्न 3.
फलन f(x) = \(\frac{x^2+2 x+1}{x^2-8 x+12}\)
हल:
f(x) = \(\frac{x^2+2 x+1}{x^2-8 x+12}\) का प्रान्त ज्ञात कीजिए ।
f(x) का परिकलित दिए गए सूत्रानुसार किया जा सकता
यदि x² - 8x + 12 = 0
या x² - 6x - 2x + 12 = 0
या x (x - 6 ) - 2 (x - 6) = 0
या (x - 6) (x - 2) = 0
लेकिन बहुपदीय फलन x² - 8x + 12, x = 6 तथा x = 2 के लिए शून्य होगा । : इस फलन का प्रान्त = R - {2, 6}

प्रश्न 4.
f(x) = \(\sqrt{(x-1)}\) द्वारा परिभाषित वास्तविक फलन का प्रान्त तथा परिसर ज्ञात कीजिए ।
हल:
दिया है - f(x) = \(\sqrt{(x-1)}\)
प्रान्त फलन के परिभाषित होने के लिए
⇒ f(x) ≥ 0
⇒ x - 1 ≥ 0
⇒ x ≤ 1
अतः फलन का प्रान्त [1, ∞)
परिसर माना कि f(x) = y

अतः y = \(\sqrt{x-1}\)
⇒ y ≥ 0 तथा y = x - 1
⇒ y ≥ 0 तथा x = y + 1
स्पष्ट है कि y ≥ 0 के लिए x ≥ 1
अतः फलन का परिसर = [0, 0)

प्रश्न 5.
f(x) = |x - 1| द्वारा परिभाषित वास्तविक फलन f का प्रान्त तथा परिसर ज्ञात कीजिए ।
हल:
माना कि
y = f(x) = |x - 1|

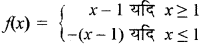
अभीष्ट फलन का प्रान्त = R तथा फलन का परिसर = [0, 0) उत्तर तथा परिसर = R⁺ ∪ {0} = ऋणेतर वास्तविक संख्याएँ

प्रश्न 6.
मान लीजिए कि f = {(x, \(\frac{x^2}{1+x^2}\)); x ∈ R} R से R में एक फलन है । f का परिसर निर्धारित कीजिए ।
हल:
प्रश्नानुसार f: R → R एक ऐसा फलन है कि
f(x) = \(\frac{x^2}{1+x^2}\) ........(1)
माना y = \(\frac{x^2}{1+x^2}\)
या x⁺ = y(1 + x⁺)
या x⁺ (1 - y) = y
या x⁺ = \(\frac{y}{1-y}\)
या x = \(\pm \sqrt{\frac{y}{1-y}}\) .........(2) जबकि x ∈ R
समीकरण (2) सेx के वास्तविक होने के लिये
\(\frac{y}{(1-y)}\) ≥ 0 तथा 1 - y ≰ 0
⇒ y ≥ 0 तथा y ≱ 1 ⇒ y ∈ [0, 1)
अर्थात् अभीष्ट फलन का परिसर = y ∈ [0, 1) है।

प्रश्न 7.
मान लीजिए कि f, g : R - R क्रमश: f(x) = x + 1, g(x) = 2x - 3, द्वारा परिभाषित है ।
f + g, f - g और \(\frac{f}{g}\) ज्ञात कीजिए ।
हल:
माना कि f (x) = x + 1, g(x) = 2x - 3
∴ f + g = f(x) + g(x) = (x + 1) + (2x - 3)
= 3x - 2
f - g = f(x) - g(x) = (x + 1) - (2x - 3)
= x + 1 - 2x + 3
= - x + 4
तथा \(\frac{f}{g}=\frac{f(x)}{g(x)}=\frac{x+1}{2 x-3}\), x ≠ \(\frac{3}{2}\)

प्रश्न 8.
मान लीजिए कि f = {(1, 1), (2, 3), (0, −1), (−1, −3)} Z से Z में, f(x) = ax + b द्वारा परिभाषित एक फलन है, जहाँ a, b कोई पूर्णांक हैं। a, b को निर्धारित कीजिए ।
हल:
माना f = {(1, 1), (2, 3), (0, -1), (-1, -3)}
यहाँ प्रान्त x = {-1, 0, 1, 2}
तथा परिसर y = {-3, -1, 1, 3}
प्रश्नानुसार y = f(x) = ax + b
x और y के मान रखने पर (1, 1) से हमें प्राप्त होगा
1 = a(1) + b
a + b = 1 .......(i)
तथा (2, 3) से 3 = a(2) + b
या 3 = 2a + b
या 2a + b = 3 ..........(ii)

समीकरण (i) व (ii) को हल करने पर

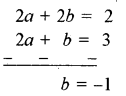
b का मान समीकरण (i) में रखने पर
a + (-1) = 1 या a = 2
∴ a = 2 तथा b = -1

प्रश्न 9.
R = {(a, b) : a, b ∈ N तथा a = b²} द्वारा परिभाषित N से N में एक सम्बन्ध R है । क्या निम्नलिखित कथन सत्य हैं ?
(i) (a, a ) ∈ R, सभी a∈ N,
(ii) (a, b) ∈ R का तात्पर्य है कि ( b, a) ∈ R
(iii) (a, b) ∈ R, (b, c) ∈ R का तात्पर्य है कि (a, c) ∈ R ? प्रत्येक दशों में अपने उत्तर का औचित्य भी बतलाइए।
हल:
(i) यह कथन सत्य नहीं है । क्योंकि जब a = 2 तब (2, 2) ∈ N अर्थात् 2 = 2² ⇒ 2 = 4 जो कि सत्य नहीं है ।

(ii) यह कथन सत्य नहीं है क्योंकि (a, b) ∈ R जो दर्शाता है कि a = b²
∴ ( b, a) ∈ R अर्थात् b = a² जो कि सत्य नहीं है । अतः (b, a) ≠ R

(iii) यह कथन सत्य नहीं है क्योंकि (a, b) ∈R, (b, c) ∈ R अर्थात् a = b², b = c² लेकिन यह a = c² पर लागू नहीं होता है । अतः (a, c) ∉ R

प्रश्न 10.
मान लीजिए कि A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} और f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}. क्या निम्नलिखित कथन सत्य हैं ?
(i) f, A से B में एक सम्बन्ध है।
(ii) f, A से B में एक फलन है ।
प्रत्येक दशा में अपने उत्तर का औचित्य बतलाइए ।
हल:
(i) यह कथन सत्य है क्योंकि फलन f, A × B का एक उपसमुच्चय है।
(ii) यह कथन सत्य नहीं है क्योंकि f में (2, 9) और (2, 11) अवयवों के प्रथम घटक दोनों युग्मों में 2 है ।

प्रश्न 11.
मान लीजिए कि f, f = {(ab, a + b) : a, b ∈ Z} द्वारा परिभाषित Z × Z का एक उपसमुच्चय है । क्या f, Z से Z में एक फलन है? अपने उत्तर का औचित्य भी स्पष्ट कीजिए ।
हल:
माना कि a = 0 तथा b = 1
∴ ab = 0.1 = 0 तथा a + b = 0 + 1 = 1
यदि a = 0 तथा b = 3
तो ab = 0.3 = 0 तथा a + b = 0 + 3 = 3
अर्थात् अवयव 0 के दो प्रतिबिम्ब 1 और 2 हैं। अत: परिभाषा के अनुसार f एक फलन नहीं है।

प्रश्न 12.
मान लीजिए कि A = {9, 10, 11, 12, 13} तथा f: A –N, f(n) = n का महत्तम अभाज्य गुणक द्वारा, परिभाषित है । fका परिसर ज्ञात कीजिए ।
हल:
जब n = 9 हो तो इसके गुणनखण्डों में 3 सबसे बड़ी अभाज्य संख्या है।
जब n = 10 तो 5 इन गुणनखण्डों में सबसे बड़ी अभाज्य संख्या है।
जब n = 11 तो 11 इन गुणनखण्डों में सबसे बड़ी अभाज्य संख्या है।
जब n = 12 तो 3 इनके गुणनखण्डों में सबसे बड़ी अभाज्य संख्या है।
जब n = 13 तो 13 इसके गुणनखण्डों में सबसे बड़ी अभाज्य संख्या है।
∴ f का परिसर = {3, 5, 11, 13}