RBSE Solutions for Class 11 Maths Chapter 2 संबंध एवं फलन Ex 2.2

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 2 संबंध एवं फलन Ex 2.2 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 2 संबंध एवं फलन Ex 2.2

प्रश्न 1.
मान लीजिए कि A = {1, 2, 3, ......, 14}, R = {(x, y) : 3x - y = 0, जहाँ x, y ∈ A} द्वारा, A से A का एक सम्बन्ध R लिखिए | इसके प्रान्त, सहप्रान्त और परिसर लिखिए ।
हल:
यहाँ A = {1, 2, 3, ......, 14}, R : A → A जबकि
R = {(x, y) : 3x - y = 0 जहाँ x, y ∈ A}
R = {(1, 3), (2, 6), (3, 9), (4, 12)}
y = 3x जहाँ x, y ∈ A
प्रान्त = {1, 2, 3, 4}
सहप्रान्त = {1, 2, 3, 4, 5, 6, ......, 14}
तथा परिसर = {3, 6, 9, 12}

प्रश्न 2.
प्राकृत संख्याओं के समुच्चय पर R = {(x, y) : y = x + 5, x संख्या 4 से कम, एक प्राकृत संख्या है x, y ∈ N} द्वारा एक सम्बन्ध R परिभाषित कीजिए। इस सम्बन्ध को (i) रोस्टर रूप में इसके प्रान्त और परिसर लिखिए ।
हल:
दिया गया सम्बन्ध R = {(x, y) : y = x + 5, x संख्या 4 से कम, एक प्राकृत संख्या है, x, y ∈ N}
रोस्टर रूप R = {(1, 6), (2, 7), (3, 8)}
R का प्रान्त = {1, 2, 3}
तथा R का परिसर = {6, 7, 8}

प्रश्न 3.
A = {1, 2, 3, 5} और B = {4, 6, 9}. A से B में एक सम्बन्ध R = {(x, y) : x और y का अन्तर विषम है, x ∈ A, y ∈ B} द्वारा परिभाषित कीजिए । R को रोस्टर रूप में लिखिए ।
हल:
प्रश्नानुसार A = {1, 2, 3, 5} तथा B {4, 6, 9} A से B में सम्बन्ध इस प्रकार दिया गया है कि
R = {(x, y) : x और y का अन्तर विषम है, x ∈ A, y ∈ B}
R = {(1, 4), (1, 6), (2, 9), (3, 4), (3, 6), (5, 4), (5, 6)}

प्रश्न 4.
आकृति समुच्चय P से Q का एक सम्बन्ध दर्शाती है । इस सम्बन्ध को
(i) समुच्चय निर्माण रूप
(ii) रोस्टर रूप में लिखिए। इसके प्रान्त तथा परिसर क्या हैं?
हल:

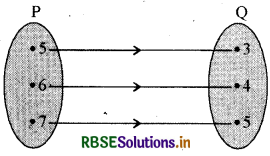
(i) चित्रानुसार P से Q में सम्बन्ध R इस प्रकार है कि x व y में 2 का अन्तर है । अर्थात्
R = {(x, y) : y = x - 2, x = 5, 6, 7 के लिए यही इस सम्बन्ध का समुच्चय निर्माण रूप है।

(ii) इस सम्बन्ध का रोस्टर रूप R = {(5, 3), (6, 4), (7, 5)}
R का प्रान्त = {5, 6, 7}
तथा R का परिसर = {3, 4, 5}

प्रश्न 5.
मान लीजिए कि A = {1, 2, 3, 4, 6}. मान लीजिए कि R, A पर {(a, b) : a, b ∈ A, संख्या a संख्या b को यथावत् विभाजित करती है} द्वारा परिभाषित एक सम्बन्ध है ।
(i) R को रोस्टर रूप में लिखिए ।
(ii) R का प्रान्त ज्ञात कीजिए ।
(iii) R का परिसर ज्ञात कीजिए ।
हल:
(i) प्रश्नानुसार A = {1, 2, 3, 4, 6}
तथा R = {(a, b) : a, b ∈ A, a संख्या b को विभाजित करती है}
अर्थात् R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)}

(ii) R का प्रान्त = {1, 2, 3, 4, 6}
(iii) R का परिसर = {1, 2, 3, 4, 6}

प्रश्न 6.
R = {(x, x + 5 ) : x ∈ {0, 1, 2, 3, 4, 5}} द्वारा परिभाषित सम्बन्ध R के प्रान्त और परिसर ज्ञात कीजिए ।
हल:
प्रश्नानुसार R = {(x, x + 5) : x = {0, 1, 2, 3, 4, 5}}
अर्थात् R = {(0,5), (1, 6), (2, 7), (3, 8), (4, 9), (5, 10)}
माना कि y = x + 5 ∈ N
∴ R का प्रान्त = {0, 1, 2, 3, 4, 5}
तथा R का परिसर = {5, 6, 7, 8, 9, 10}

प्रश्न 7.
सम्बन्ध R = {(x, x³): x संख्या 10 से कम एक अभाज्य संख्या है} को रोस्टर रूप में लिखिए ।
हल:
यहाँ R = {(x, x) : x संख्या 10 से कम एक अभाज्य संख्या है }
∴ यहाँ पर x ∈ {2, 3, 5, 7}
∴ R = {(2, 8), (3, 27), (5, 125), (7, 343)}
यही इसका रोस्टर रूप है ।

प्रश्न 8.
मान लीजिए कि A = {x, y, z} और B = {1, 2}, A से B के सम्बन्धों की संख्या ज्ञात कीजिए ।
हल:
प्रश्नानुसार A = {x, y, z} तथा B = {1, 2}
∴ A × B = {x, y, z} × {1, 2}
= {(x, 1), (x, 2), (y, 1), (y, 2), (z, 1), (z, 2)}
अर्थात् n(A × B) = 6
सम्बन्धों की कुल संख्या = A × B के उपसमुच्चयों की संख्या
= 2⁶ = 64

प्रश्न 9.
मान लीजिए कि R, Z पर, R = {(a, b ) : a, b ∈ Z, a - b एक पूर्णांक है}, द्वारा परिभाषित एक सम्बन्ध है । R के प्रान्त तथा परिसर ज्ञात कीजिए ।
हल:
यहाँ R = {(a, b) : a, b ∈ Z, a b एक पूर्णांक है}
प्रश्नानुसार a b एक पूर्णांक है अतः a और b सम या विषम दोनों ही हो सकते हैं ।
∴ R का प्रान्त = Z (पूर्णांक) ∵ a एक पूर्णांक है ।
तथा R का परिसर = Z (पूर्णांक) ∵ b एक पूर्णांक है ।