RBSE Solutions for Class 11 Maths Chapter 2 संबंध एवं फलन Ex 2.1

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 2 संबंध एवं फलन Ex 2.1 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 2 संबंध एवं फलन Ex 2.1

प्रश्न 1.
यदि (\(\frac{x}{3}\) + 1, y - \(\frac{2}{3}\)) = \(\left(\frac{5}{3}, \frac{1}{3}\right)\), तो x तथा y ज्ञात कीजिए।
हल:
प्रश्नानुसार (\(\frac{x}{3}\) + 1, y - \(\frac{2}{3}\)) = \(\left(\frac{5}{3}, \frac{1}{3}\right)\)

यहाँ क्रमित युग्म समान है, अतः संगत घटकों की तुलना से

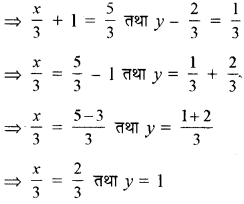
या x = 2, y = 1

प्रश्न 2.
यदि समुच्चय A में 3 अवयव हैं तथा समुच्चय B = {3, 4, 5, तो (A × B) में अवयवों की संख्या ज्ञात कीजिए ।
हल:
प्रश्नानुसार n(A) = 3, n(B) = 3
∴ n(A × B) = n (A) . n (B) = 3 × 3 = 9
अर्थात् समुच्चय (A × B) में अवयवों की संख्या 9 है।

प्रश्न 3.
यदि G = {7, 8} और H = {5, 4, 2}, तो G × H और H × G ज्ञात कीजिए |
हल:
प्रश्नानुसार G = {7, 8} तथा H = {5, 4, 2}
G × H= {7, 8} × {5, 4, 2}
= {(7, 5), (7, 4), (7, 2), (8, 5), (8, 4), (8, 2)}

तथा H × G = {5, 4, 2} × {7, 8}
= {(5, 7), (5, 8), (4, 7), (4, 8), (2, 7), (2, 8)}

प्रश्न 4.
बतलाइए कि निम्नलिखित कथनों में से प्रत्येक सत्य है अथवा असत्य है । यदि कथन असत्य है, तो दिए गए कथन को सही बनाकर लिखिए ।
(i) यदि P = {m, n} और Q = {n, m}, तो P × Q = {(m, n), (n, m)}
(ii) यदि A और B अरिक्त समुच्चय हैं, तो A × B क्रमित युग्मों (x, y) का एक अरिक्त समुच्चय है, इस प्रकार कि x ∈ A तथा y ∈ B.
(iii) यदि A = {1, 2}, B = {3, 4}, तो A × (B ∩ Φ) = 0.
हल:
(i) यह कथन असत्य है । यहाँ n (P) = 2 तथा (Q) = 2
∴ n(P × Q) = 2 × 2 = 4
यदि P = {m, n} तथा Q = {n, m}
अत: P × Q = {(m, n), (m, m), (n, n), (n, m)}

(ii) कथन असत्य है ।
कथन A × B क्रमित युग्मों (x, y) का वह अरिक्त समुच्चय है जिसमें x ∈ A तथा y ∈ B
∵ A × B = {(x, y) : x ∈ A, y ∈ B}

(iii) यह कथन सत्य है चूँकि B ∩ Φ = Φ
इस प्रकार A × (B ∩ Φ) = A × Φ = Φ
क्योंकि Φ में कोई अवयव नहीं होता है।

प्रश्न 5.
यदि A = {-1, 1}, तो A × A × A ज्ञात कीजिए ।
हल:
यहाँ A = {-1, 1}
तब A × A = {−1, 1} × {−1, 1}
= {(-1, -1), (-1, 1), (1, -1), (1, 1)}

∴ A × A × A = {−1, 1} × {(-1, -1), (−1, 1), (1, −1), (1, 1)}
= {(−1, −1, −1), (−1, −1, 1), (−1, 1, −1), (−1, 1, 1), (1, −1, −1), (1, −1, 1), (1, 1, −1), (1, 1, 1)}

प्रश्न 6.
यदि A × B = {(a, x), (a, y), (b, x), (b, y)} तो A तथा B ज्ञात कीजिए ।
हल:
प्रश्नानुसार A × B = {(a, x), (a, y), (b, x), (b, y)}
A = {a, b} तथा B = {x, y}
A में क्रमित युगमों के प्रथम घटक होंगे
A = {a, b}
इसी प्रकार B में क्रमित युगमों के द्वितीय घटक होंगे
अर्थात् B = {x, y}
∴ A = {a, b} तथा B = {x, y}

प्रश्न 7.
मान लीजिए कि A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} तथा D = {5, 6, 7, 8} सत्यापित कीजिए कि
(i) A × (B ∩ C) = (A × B) ∩ (A × C),
(ii) A × C, B × D का एक उपसमुच्चय है ।
हल:
(1) A × (B ∩ C) = (A × B) ∩ (A × C),
L.H.S. = A × (B ∩ C)
= {1, 2} × [{1, 2, 3, 4} ∩ {5, 6}]
= {1, 2} × Φ
R.H.S. = (A × B) ∩ (A × C)
= [{1, 2} × {1, 2, 3, 4}]~[{1, 2} × {5,6}]
= {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1),
= Φ
अतः L.H.S. = R.H.S
(2, 2), (2, 3), (2, 4)} ∩ {(1, 5), (1, 6), (2, 5), (2, 6)}
= R.H.S.
अर्थात् A × (B ∩ C) = (A × B) ∩ (A × C)

(ii) A × C = {1, 2} × {5, 6}
= {(1, 5), (1, 6), (2, 5), (2, 6)}
तथा B × D= {1, 2, 3, 4} × {5,6, 7, 8}
= {(1, 5), (1, 6), (1, 7), (1, 8), (2, 5), (2, 6), (2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8), (4, 5), (4, 6), (4, 7), (4, 8)}
यहाँ हम देखते हैं कि A × C के समस्त अवयव समुच्चय B × D में हैं
∴ A × C ⊂ B × D

प्रश्न 8.
मान लीजिए कि A = {1, 2} और B {3, 4}, A × B लिखिए | A × B के कितने उपसमुच्चय होंगे? उनकी सूची बनाइए ।
हल:
प्रश्नानुसार A = {1, 2} B = {3, 4}
∴ A × B = {1, 2} × {3, 4}
= {(1, 3), (1, 4), (2, 3), (2, 4)}
A × B में 4 अवयव हैं अतः इसके कुल उप-समुच्चय 2⁴ = 16 होंगे जो निम्नलिखित होंगे
= Φ, {(1, 3)}, {(1, 4)}, {(2, 3)}, {(2, 4)}, {(1, 3), (1, 4)}, {(1, 3), (2, 3)}, {(1, 3), (2, 4)}, {(1, 4), (2, 3)}, {(1, 4), (2, 4)}, {(2, 3), (2, 4)}, {(1, 3), (1, 4), (2, 3)}, {(1, 3), (1, 4), (2, 4)}, {(1, 3), (2, 3), (2, 4)}, {(1, 4), (2, 3), (2, 4)}, {(1, 3), (1, 4), (2, 3), (2, 4)

प्रश्न 9.
मान लीजिए कि A और B दो समुच्चय हैं, जहाँ n(A) = 3 और n(B) = 2. यदि (x, 1), (y, 2), (z, 1), A × B में हैं, तो A और B को ज्ञात कीजिए, जहाँ x, y और z भिन्न-भिन्न अवयव हैं ।
हल:
प्रश्नानुसार n (A) = 3, n (B) = 2
∴ n(A × B), = n(A) . n(B) = 3 × 2 = 6
यदि (x, 1), (, 2), (z, 1) A × B में हैं, तो A = {x, y, z} {1, 2} उत्तर
तथा B = {1, 2}

प्रश्न 10.
कार्तीय गुणन A × A में 9 अवयव हैं, जिनमें (-1, 0) तथा (0, 1) भी है । समुच्चय A ज्ञात कीजिए तथा A × A के शेष अवयव भी ज्ञात कीजिए ।
हल:
(-1, 0) ∈ A × A ⇒ -1 ∈ A तथा 0 ∈ A
⇒ - 1, 0 ∈ A
तथा ( 0, 1 ) ∈ A
⇒ 0 ∈ A तथा I ∈ A
⇒ 0, 1 ∈ A
⇒ −1, 0, 1 ∈ A
∴ A = {−1, 0, 1}
∴ A × A = {-1, 0, 1} × {−1, 0, 1}
= {(−1, −1), (-1, 0), (−1, 1), (0, −1), (0, 0), (0, 1), (1, −1), (1, 0), (1, 1)}
इसमें (−1, 0), (0, 1) सम्मिलित हैं । इसलिये शेष अवयव होंगे {(−1, −1), (−1, 1), (0, −1), (0, 0), (1, −1), (1, 0), (1, 1)}