RBSE Solutions for Class 11 Maths Chapter 1 समुच्चय विविध प्रश्नावली

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 1 समुच्चय विविध प्रश्नावली Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 1 समुच्चय विविध प्रश्नावली

प्रश्न 1.
निम्नलिखित समुच्चयों में से कौन किसका उपसमुच्चय है, इसका निर्णय कीजिए
A = {x : x ∈ R तथा x² - 8x + 12 = 0 को सन्तुष्ट करने वाली सभी वास्तविक संख्याएँ x}, B = {2, 4, 6}
C = {2, 4, 6, 8, . . .}, D = {6}.
हल:
∴ x² – 8x + 12 = 0
या x² - 6x - 2x + 12 = 0
या x(x -.6) - 2(x - 6) = 0
या (x - 6) (x - 2) = 0
या x - 6 = 0 या x - 2 = 0
= {2, 4, 6},

या x = 6 या x = 2
A = {2, 6}, B = {2, 4, 6}
{2, 4, 6, 8 ......} तथा D = {6}

(i) समुच्चय A के अवयव 2, 6 समुच्चय B में भी हैं ।
⇒ A ⊂ B
(ii) समुच्चय A के अवयव 2, 6 समुच्चय C में भी हैं ।
⇒ A ⊂ C
(iii) समुच्चय B के अवयव 2, 4, 6 समुच्चय C में हैं ।
⇒ B ⊂ C
(iv) समुच्चय D का अवयव 6 समुच्चय A, B तथा C में है ।
⇒ D ⊂ A, D ⊂ B, D ⊂ C

प्रश्न 2.
ज्ञात कीजिए कि निम्नलिखित में से प्रत्येक कथन सत्य है या असत्य है । यदि सत्य है, तो उसे सिद्ध कीजिए। यदि असत्य है, तो एक उदाहरण दीजिए ।
(i) यदि x ∈ A तथा A ∈ B, तो x ∈ B
(ii) यदि A ⊂ B तथा B ∈ C, तो A ∈ C
(iii) यदि A ⊂ B तथा B ⊂ C, तो A ⊂ C
(iv) यदि A ⊂ B तथा B ⊂ C, तो A ⊂ C
(v) यदि x ∈ A तथा A ∉ B, तो x ∈ B
(vi) यदि A ⊂ B तथा x ∉ B, तो x ∉ A
हल:
(i) दिया गया कथन असत्य है। माना कि A = {1}, B = {{1}, 2} है। स्पष्ट है कि 1 ∈ A, A ∈ B परन्तु 1 ∉ समुच्चय B क्योंकि 1, B में नहीं है ।
(ii) दिया गया कथन असत्य है। माना कि A = {1}, B = {1, 2} तथा C = {{1, 2}, 3} है । यहाँ समुच्चय A का अवयव समुच्चय B में है : A ⊂ B अवयव {1, 2} समुच्चय C में है ⇒ B ∈ C परन्तु A = {1} समुच्चय C में नहीं है ।

(iii) दिया गया कथन सत्य है। A ⊂ B ⇒ यदि x ∈ A तथा X ∈ B
परन्तु B ⊂ C ⇒ यदि X ∈ B तब x ∈ C यदि x ∈ A तब x ∈ C ⇒ A ⊂ C

(iv) दिया गया कथन असत्य है। माना कि A = {1, 2}, B = {2, 3}, C = {1, 2, 5} है। समुच्चय A के सभी अवयव 1, 2 समुच्चय B में नहीं हैं ∴ A ⊄ B
समुच्चय B के सभी अवयव 2, 3 समुच्चय C में नहीं हैं ।
∴ B ⊄ C
परन्तु समुच्चय A के सभी अवयव 1, 2 समुच्चय C में हैं ।
∴ A ⊂ C

(v) दिया गया कथन असत्य है । माना कि A = {1, 2}, B = {2, 3, 4, 5}
समुच्चय A के सभी अवयव 1, 2 समुच्चय B में नहीं हैं।
∴ A ⊄ B
समुच्चय A का अवयव 1 समुच्चय B में नहीं है ।
∴ x ∉ B

(vi) दिया गया कथन सत्य है । A ⊂ B अर्थात् यदि x ∈ A तब x ∈ B यदि x ∉ B तथा x ∉ A

प्रश्न 3.
मान लीजिए A, B और C ऐसे समुच्चय हैं कि A ∪ B = A ∪ C तथा A ∩ B = A ∩ C, तो दर्शाइए कि B = C ।
हल:
दिया है
A ∪ B = A ∪ C .....(i)
A ∩ B = A ∩ C .......(ii)

समीकरण (i) से
A ∪ B = A ∪ C
(A ∪ B) ∩ B = (A ∪ C) ∩ B
⇒ (A ∩ B)
⇒ B = (A ∪ C) ∩ B
⇒ (C ∩ B) = B
⇒ (A ∩ C) U (B ∩ C) = B
[∵ (A ∪ B) ∩ B = B]
⇒ (A ∩ B) ∪ (C ∩ B) = B
⇒ (A ∩ C) ∪ (B ∩ C ) = B
[∵ B ∩ C = C ∩ B तथा समीकरण (ii) ]
⇒ (A ∪ B) ∪ C = B
⇒ (A ∪ C) ∩ C = B [समीकरण (i) से]
⇒ C = B [∵ (A ∪ C) ∩ C = C]
⇒ B = C

प्रश्न 4.
दिखाइए कि निम्नलिखित चार प्रतिबन्ध तुल्य हैं-
(i) A ⊂ B
(iii) A ∪ B = B
(ii) A - B = Φ
(iv) A ∩ B = A
हल:
(i) व (ii) की तुल्यता के लिए-
दिया है - ACB तथा x ∈ A ⇒ x ∈ B
अतः A - B में एक भी अवयव नहीं होगा
अर्थात् A - B = Φ इति सिद्धम्

(ii) व (iii) की तुल्यता के लिए-
दिया है - A - B = Φ
Φ ⇒ A ∩ B = Φ
अर्थात् A व B में एक भी अवयव उभयनिष्ठ नहीं है ।
⇒ A का प्रत्येक अवयव B का अवयव है
⇒ A ⊂ B अर्थात् A ∪ B ⊂ B
पुन: B ⊂ B अर्थात् A ∪ B ⊂ B
अतः स्पष्ट है B ⊂ A ∪ B या A ∪ B = B इति सिद्धम्

(iii) व (iv) की तुल्यता के लिए-
दिया है
A ∪ B = B
⇒ A ⊂ A ∪ B = B
⇒ A ⊂ B
पुन: A ⊂ A अत: A ⊂ A ∩ B
अर्थात् A ∩ B ⊂ A
या A ∩ B = A इति सिद्धम्

(iv) व (i) की तुल्यता के लिए-
दिया है
A ∩ B = A तथा A ∩ B ⊂ B ⇒ A ⊂ B इति सिद्धम्

प्रश्न 5.
दिखाइए कि यदि A ⊂ B, तो C - B ⊂ C - A.
हल:
A ⊂ B ⇒ x ∈ A तथा x ∈ B .....(i)
और यदि x ∉ B तो x ∉ A .....(ii)

माना x ∈ (C - B)
⇒ x ∈ C तथा x ∈ B
⇒ x ∈ C तथा x ∈ A
[समीकरण (i) से]
⇒ x ∈ (C – A)
(C - B) ⊂ (C - A) इति सिद्धम्

प्रश्न 6.
मान लीजिए कि P(A) = P (B), सिद्ध कीजिए कि A = B
हल:
माना कि x समुच्चय A का कोई अवयव है। तब एक उपसमुच्चय X ऐसा माना जिसमें x ∈ A अतः
X ⊂ A ⇒ X ∈ P(A)
⇒ X ∈ P(B)
[∵ P(A) = P(B)]
∴ X ∈ B या x∈ B
अर्थात् यदि x ∈ A तब x∈ B
⇒ A ⊂ B
पुनः माना कि y समुच्चय B का कोई अवयव है ....(i)
⇒ तब समुच्चय B का कोई उपसमुच्चय Y ऐसा माना कि y ∈ B
y ∈ B ⇒ y ∈ P(B)
⇒ y ∈ P(A)
⇒ y ∈ A [∵ P(B) = P(A)]
⇒ यदि y, ∈ B तब y∈ A
⇒ B ⊂ A ...(ii)
समीकरण (i) व (ii) से A = B ( इति सिद्धम्)

प्रश्न 7.
किन्हीं भी समुच्चयों A तथा B के लिए, क्या यह सत्य है कि P(A) ∪ P(B) = P (A ∪ B) ? अपने उत्तर का औचित्य बताइए ।
हल:
दिया गया कथन असत्य है । यदि A = {a}, B = {b}
तथा A ∪ B = {a, b}
P(A) = {Φ, {a}}, P(B) = {Φ, {b}}
P(A) ∪ P(B) = {Φ, {a}, {b}} .......(i)
अब A ∪ B = {a, b}
∴ P(A ∪ B) = {Φ, {a}, {b}, {a, b}} .......(ii)
समीकरण (i) तथा (ii) के अनुसार
P(A) ∪ P(B) ≠ P(A ∪ B)
अतः उपर्युक्त कथन असत्य है ।

प्रश्न 8.
किन्हीं दो समुच्चयों A तथा B के लिए सिद्ध कीजिए कि
A = (A ∩ B) ∪ (A - B ) और A ∪ ( B - A ) = (A ∪ B)
हल:
(i) R.H.S. = (A ∩ B) ∪ ( A - B)
= (A ∩ B) ∪ (A ∩ B)
[∵ A - B = A ∩ B']
= A ∩ (B ∪ B') ( वितरण गुण)
= A ∩ U [U सार्वत्रिक समुच्चय ]
= A = L.H.S.
अत: (A ∩ B) ∪ (A - B) = A

(ii) L.H.S. = A ∪ ( B - A)
= A ∪ (B ∩ A') [∵ B - A = B ∩ A']
= (A ∪ B) ∩ (A ∪ A) (वितरण गुण)
= (A ∪ B) ∩ U [U सार्वत्रिक समुच्चय ]
= A ∪ B = R.H.S.
अत: A ∪ (B - A) = A ∪ B.

प्रश्न 9.
समुच्चयों के गुणधर्मों का प्रयोग करके सिद्ध कीजिए कि
(i) A ∪ (A ∩ B) = A
(ii) A ∩ (A ∪ B ) = A.
हल:
(i) A ∪ (A ∩ B) = A
L.H.S. A ∪ (A ∩ B)
= (A ∪ A) ∩ (A ∪ B) (वितरण गुण)
= A ∩ (A ∪ B) [∵ A ∪ A = A] [A ⊂ A ∪ B]
= A
= R.H.S.
A ∪ (A ∩ B) = A

(ii) A ∩ (A ∪ B) = A
L.H.S. = A
(A ∪ B)
= (A ∩ A) ∪ (A ∩ B) (वितरण गुण)
= A ∪ (A ∩ B)[A ∩ A = A]
= A [A ∩ B ⊂ A]
= A
= R.H.S.
अत: A ∩ (A ∪ B) = A (इति सिद्धम्)

प्रश्न 10.
दिखलाइए कि A ∩ B = A ∩ C का तात्पर्य B = C आवश्यक रूप से नहीं होता है।
हल:
माना कि A = {1, 2}, B = {1, 7}, C = {1, 4}
∴ A ∩ B = {1, 2} ∩ {1, 7} = {1}
तथा A ∩ C = {1, 2} ∩ {1, 4} = {1}
⇒ A ∩ B = A ∩ C
परन्तु B ≠ C
⇒ यदि A ∩ B = AC तो आवश्यक नहीं है कि B = C.

प्रश्न 11.
मान लीजिए कि A और B समुच्चय हैं। यदि किसी समुच्चय X के लिए A ∩ X = B ∩ X = Φ तथा A ∪ X = B ∪ X, तो सिद्ध कीजिए कि A = B .
[संकेत: A = A ∩ (A ∪ X), B = B ∩ (B ∪ X) वितरण नियम का प्रयोग कीजिए ]
हल:
प्रश्नानुसार दिया गया है कि A ∪ X = B ∪ X जबकि X कोई समुच्चय है ।
⇒ A ∩ (A ∪ X) = A ∩ (B ∪ X)
⇒ A = (A ∩ B) ∪ (A ∩ X)
[: A ∩ (A ∪ X) = A]
= (A ∩ B) ∪
[∵ A ∩ X = Φ (दिया है) ]
= A ∩ B ⇒ A ⊂ B
पुन: A ∪ X = B ∪ X
⇒ B ∩ (A ∪ X) = B ∩ (B ∪ X)
⇒ (B ∩ A) ∪ (B ∩ X) = B [∵ B ∩ (B ∪ X) = B]
⇒ (B ∩ A) ∪ Φ = B [B ∩ X = Φ (दिया है ) ]
⇒ B ∩ A = B
⇒ A ∩ B = B ⇒ B ⊆ A ............ (ii)
समीकरण (i) व (ii) से A = B ( इति सिद्धम्)

प्रश्न 12.
ऐसे समुच्चय A, B और C ज्ञात कीजिए ताकि A ∩ B, B ∩ C तथा A ∩ C आरिक्त समुच्चय हों और A ∩ B ∩ C = Φ
हल:
माना कि A = {1, 2}, B = {2, 3} तथा C = {1, 3}
A ∩ B = {1, 2} ∩ {2, 3} = {2}
B ∩ C = {2, 3} ∩ {1, 3} = {3}
C ∩ A = {1, 3} ∩ {1, 2} = {1}
इस प्रकार A ∩ B, B ∩ C, C ∩ A रिक्त समुच्चय नहीं हैं ।
∴ A ∩ B ∩ C = (A ∩ B) ∩ C
= {2} ∩ {1, 3} = Φ ( इति सिद्धम् )
अर्थात् A ∩ B ∩ C = Φ

प्रश्न 13.
किसी विद्यालय के 600 विद्यार्थियों के सर्वेक्षण से ज्ञात हुआ कि 150 विद्यार्थी चाय, 225 विद्यार्थी कॉफी तथा 100 विद्यार्थी चाय और कॉफी दोनों पीते हैं। ज्ञात कीजिए कि कितने विद्यार्थी न तो चाय पीते हैं और न कॉफी पीते हैं।
हल:
माना कि T चाय पीने वाले विद्यार्थियों तथा कॉफी पीने वाले विद्यार्थियों के समुच्चय हैं और U सर्वेक्षण किये गये विद्यार्थियों का समुच्चय है ।
अतः प्रश्नानुसार n(U) = 600,
n(T) = 150, n(C) = 225,
n(T ∩ C) = 100

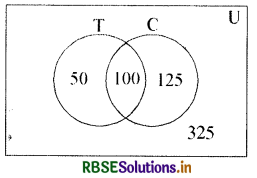
n(T ∪ C) = n(T) + n (C) - n (T ∩ C)
= 150 + 225 - 100
= 275
अर्थात् ये विद्यार्थी चाय या कॉफी पीते हैं या चाय और कॉफी दोनों पीते हैं ।
कुल विद्यार्थी = 600
पुन: n(T ∪ C)' = n(U) - n (T ∪ C)
⇒ n(T ∪ C)' = 600 - 275
⇒ n(T ∪ C)' = 325
अतः 325 विद्यार्थी न तो चाय पीते हैं और न कॉफी पीते हैं ।

प्रश्न 14.
विद्यार्थियों के एक समूह में, 100 विद्यार्थी हिन्दी, 50 विद्यार्थी अंग्रेजी तथा 25 विद्यार्थी दोनों भाषाओं को जानते हैं । विद्यार्थियों में से प्रत्येक या तो हिन्दी या अंग्रेजी जानता है । समूह में कुल कितने विद्यार्थी हैं?
हल:
माना कि हिन्दी जानने वाले विद्यार्थियों का समुच्चय H तथा अंग्रेजी जानने वाले विद्यार्थियों का समुच्चय E है ।
अतः प्रश्नानुसार n (H) = 100, n (E) = 50 तथा n (H ∩ E) = 25
n(H ∪ E) = n(H) + n (E) - n (H ∩ E)
= 100 + 50 - 25
= 125
अर्थात् ऐसे विद्यार्थी जो हिन्दी या अंग्रेजी जानते हैं = 125.

प्रश्न 15.
60 लोगों के सर्वेक्षण में पाया गया कि 25 लोग समाचार-पत्र H, 26 लोग समाचार पत्र T, 26 लोग समाचार-पत्र I, 9 लोग H तथा I दोनों, 11 लोग H तथा T दोनों, 8 लोग T तथा । दोनों और 3 लोग तीनों ही समाचार-पत्र पढ़ते हैं, तो निम्नलिखित ज्ञात कीजिए-
(i) कम से कम एक समाचार-पत्र पढ़ने वालों की संख्या ।
(ii) ठीक-ठीक केवल एक समाचार-पत्र पढ़ने वालों की संख्या ।
हल:
(i) माना कि H, T तथा I उन समाचार पत्रों का समुच्चय है जो लोगों द्वारा पढ़े जाते हैं । यहाँ

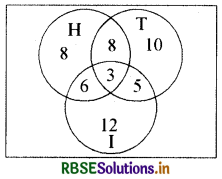
n(H) = 25, n(T) = 26, n (I) = 26, n (H ∩ T) = 11, n('I ∩ I) = 8, n (H ∩ I) = 9, n(H ∩ T ∩ I) = 3
n(H ∩ T ∪ I) = n (H) + n (T) + n(I) - (H ∩ T) - n(T ∩ I) – n(H ∩ I) + n(H ∩ T ∩ I)
मान रखने पर = 25 + 26 + 26 - 11 - 8 - 9 + 3
= 77 - 28 + 3
= 80 - 28
= 52
अतः कम से कम एक समाचार पत्र पढ़ने वालों की संख्या = 52 है ।

(ii) केवल H और T समाचार - पत्र पढ़ने वालों की संख्या = 11 - 3 = 8
केवल T और I समाचार पत्र पढ़ने वालों की संख्या = 8 - 3 = 5
केवल I और H समाचार पत्र पढ़ने वालों की संख्या = 9 - 3 = 6
तीनों समाचार - पत्र पढ़ने वालों की संख्या 3 केवल एक समाचार-पत्र पढ़ने वालों की संख्या
= 52 - (8 + 5 + 6 + 3)
= 52 - 22 = 30

प्रश्न 16.
एक सर्वेक्षण में पाया गया कि 21 लोग उत्पाद A, 26 लोग उत्पाद B, 29 लोग उत्पाद C पसन्द करते हैं । यदि 14 लोग उत्पाद A तथा B, 12 लोग उत्पाद C तथा A, 14 लोग उत्पाद B तथा C और 8 लोग तीनों ही उत्पादों को पसन्द करते हैं । ज्ञात कीजिए कि कितने लोग केवल उत्पाद C को पसन्द करते हैं।
हल:
प्रश्नानुसार n (A) = 21, n(B) = 26, n(C) = 29

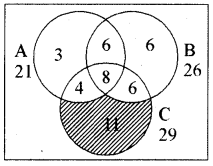
∴ n(A ∩ B) = 14
n(A ∩ C) = 12
n(B ∩ C) = 14
तथा n(A ∩ B ∩ C) = 8
n(C केवल) = 29 (4 + 8 +6)
= 29 - 18 = 11
अर्थात् उत्पाद C को पसन्द करने वाले लोग = 11