RBSE Solutions for Class 10 Maths Chapter 7 निर्देशांक ज्यामिति Ex 7.3

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 7 निर्देशांक ज्यामिति Ex 7.3 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 7 निर्देशांक ज्यामिति Ex 7.3

प्रश्न 1.
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष हैं :
(i) (2, 3), (-1, 0), (2, -4)
हल-
माना कि ∆ABC के शीर्ष A(2, 3), B(-1, 0) और C(2, -4) हैं।
यहाँ x₁ = 2, x₂ = -1, x₃ = 2
y₁ = 3, y₂ = 0, y₃ = -4
∴ ∆ABC का क्षेत्रफल = \(\frac{1}{2}\) [x₁(y₂ - y₃) + x₂ (y₃ - y₁) + x₃(y₁ - y₂)]
= \(\frac{1}{2}\) [2 × (0 + 4) - 1 × (-4 - 3) + 2 × (3 - 0)]
= \(\frac{1}{2}\) [8 + 7 + 6]
= \(\frac{21}{2}\)
= 10.5 वर्ग मात्रक

(ii) (-5, -1), (3, -5), (5, 2)
हल-
माना कि ∆ABC के शीर्ष A(-5, -1), B(3, -5) और C(5, 2) हैं।
यहाँ x₁ = -5, x₂ = 3, x₃ = 5
y₁ = -1, y₂ = -5, y₃ = 2
∴ ∆ABC का क्षेत्रफल = \(\frac{1}{2}\) [x₁(y₂ - y₃) + x₂ (y₃ - y₁) + x₃(y₁ - y₂)]
= \(\frac{1}{2}\) [-5(-5 - 2) + 3(2 + 1) + 5(-1 + 5)]
= \(\frac{1}{2}\) [35 + 9 + 20]
= \(\frac{1}{2}\) × 64
= 32 वर्ग मात्रक

प्रश्न 2.
निम्नलिखित में से प्रत्येक में 'k' का मान ज्ञात कीजिए, ताकि तीनों बिन्दु संरेखी हों :
(i) (7, -2), (5, 1), (3, k)
हल-
माना कि दिए गए बिन्दु A(7, -2), B(5, 1) और C(5, k) हैं।
यहाँ x₁ = 7, x₂ = 5, x₃ = 3
y₁ = -2, y₂ = 1, y₃ = k
यदि तीन बिन्दु संरेखी होते हों तो त्रिभुज का क्षेत्रफल शून्य होना चाहिए।
अर्थात् \(\frac{1}{2}\) [x₁(y₂ - y₃) + x₂ (y₃ - y₁) + x₃(y₁ - y₂)] = 0
या \(\frac{1}{2}\) [7(1 - k) + 5(k + 2) + 3(-2 - 1)] = 0
या 7 - 7k + 5k + 10 - 9 = 0
या -2k + 8 = 0
या -2k = -8
या k = 4
अतः k = 4 के लिए तीनों बिन्दु संरेख हैं।

(ii) (8, 1), (k, -4), (2, -5)
हल-
माना कि दिए गए बिन्दु A(8, 1), B(k, -4) और C(2, -5) हैं।
यहाँ x₁ = 8, x₂ = k, x₃ = 2
y₁ = 1, y₂ = -4, y₃ = -5
यदि तीन बिन्दु संरेखी हों, तो त्रिभुज का क्षेत्रफल शून्य होना चाहिए।
अर्थात्, \(\frac{1}{2}\) [x₁(y₂ - y₃) + x₂ (y₃ - y₁) + x₃(y₁ - y₂)] = 0
या \(\frac{1}{2}\) [8(-4 + 5) + k(-5 - 1) + 2(1 + 4)] = 0
या 8 - 6k + 10 = 0
या -6k = -18
या k = 3
अतः k = 3 के लिए तीनों बिन्दु संरेख हैं।

प्रश्न 3.
शीर्षों (0, -1), (2, 1) और (0, 3) वाले त्रिभुज की भुजाओं के मध्य-बिन्दुओं से बनने वाले त्रिभुज का क्षेत्रफल ज्ञात कीजिए। इस क्षेत्रफल का दिए हुए त्रिभुज के क्षेत्रफल के साथ अनुपात ज्ञात कीजिए।
हल-
माना कि दिए गए त्रिभुज ABC के शीर्ष A(0, -1), B(2, 1) और C(0, 3) हैं।
तथा D, E, F क्रमशः AB, BC, CA के मध्य बिन्दु हैं।
अतः मध्य-बिन्दु सूत्र से

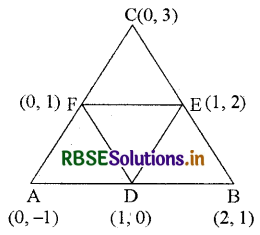
D के निर्देशांक = \(\left(\frac{0+2}{2}, \frac{-1+1}{2}\right)\) = (1, 0)
E के निर्देशांक = \(\left(\frac{2+0}{2}, \frac{1+3}{2}\right)\) = (1, 2)
F के निर्देशांक = \(\left(\frac{0+0}{2}, \frac{3-1}{2}\right)\) = (0, 1)
∴ ∆DEF के शीर्षों के निर्देशांक D(1, 0), E(1, 2), F(0, 1) हैं।
यहाँ x₁ = 1, x₂ = 1, x₃ = 0
y₁ = 0, y₂ = 2, y₃ = 1
∆DEF का क्षेत्रफल = \(\frac{1}{2}\) [x₁(y₂ - y₃) + x₂ (y₃ - y₁) + x₃(y₁ - y₂)]
= \(\frac{1}{2}\) [1(2 - 1) + 1(1 - 0) + 0(0 - 2)]
= \(\frac{1}{2}\) [1 + 1 + 0]
= \(\frac{2}{2}\)
= 1 वर्ग मात्रक
∆ABC में,
x₁ = 0, x₂ = 2, x₃ = 0
y₁ = -1, y₂ = 1, y₃ = 3
∆ABC का क्षेत्रफल = \(\frac{1}{2}\) [x₁(y₂ - y₃) + x₂ (y₃ - y₁) + x₃(y₁ - y₂)]
= \(\frac{1}{2}\) [0(1 - 3) + 2(3 + 1) + 0 (-1 - 1)]
= \(\frac{1}{2}\) [0 + 8 + 0]
= \(\frac{8}{2}\)
= 4 वर्ग मात्रक
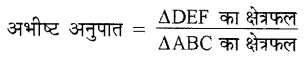=   \(\frac{1}{4}\)
अर्थात् 1 : 4 
अतः दोनों त्रिभुजों के क्षेत्रफलों का अनुपात = 1 : 4

प्रश्न 4.
उस चतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष, इसी क्रम में (-4, -2), (-3, -5), (3, -2) और (2, 3) हैं।
हल-
माना कि दी गई चतुर्भुज ABCD के निर्देशांक A(-4, -2), B(-3, -5), C(3, -2) और D(2, 3) हैं।
AC को मिलाइए, तो चतुर्भुज ABCD, दो त्रिभुजों में विभाजित हो जाता है।
अर्थात् ∆ABC और ∆CDA

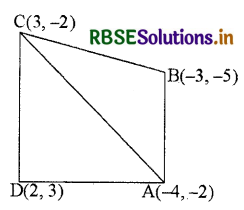
∆ABC में, यहाँ x₁ = -4, x₂ = -3, x₃ = 3
y₁ = -2, y₂ = -5, y₃ = -2
∆ABC का क्षेत्रफल = \(\frac{1}{2}\) [x₁(y₂ - y₃) + x₂ (y₃ - y₁) + x₃(y₁ - y₂)]
= \(\frac{1}{2}\) [-4(-5 + 2) + (-3) (-2 + 2) + 3(-2 + 5)]
= \(\frac{1}{2}\) [12 + 0 + 9] 
= \(\frac{21}{2}\) वर्ग मात्रक
∆CDA में,
x₁ = 3, x₂ = 2, x₃ = -4
y₁ = -2, y₂ = 3, y₃ = -2
∆CDA का क्षेत्रफल = \(\frac{1}{2}\) [x₁(y₂ - y₃) + x₂ (y₃ - y₁) + x₃(y₁ - y₂)]
= \(\frac{1}{2}\) [3(3 + 2) + 2(-2 + 2) + (-4) (-2 - 3)]
= \(\frac{1}{2}\) [15 + 0 + 20]
= \(\frac{35}{2}\) वर्ग मात्रक
अब, चतुर्भुज ABCD का क्षेत्रफल = (∆ABC का क्षेत्रफल) + (∆ACD का क्षेत्रफल)
= \(\frac{21}{2}+\frac{35}{2}\)
= \(\frac{56}{2}\)
= 28 वर्ग मात्रक 
अतः अभीष्ट चतुर्भुज का क्षेत्रफल = 28 वर्ग मात्रक

प्रश्न 5.
कक्षा IX में आपने पढ़ा है (अध्याय 9, उदाहरण 3) कि किसी त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है। उस त्रिभुज ABC के लिए इस परिणाम का सत्यापन कीजिए जिसके शीर्ष A(4, -6), B(3, -2) और C(5, 2) हैं।
हल-
प्रश्नानुसार ∆ABC के शीर्षों के निर्देशांक, A(4, -6), B(3, -2) और C(5, 2) हैं।
माना कि CD एक माध्यिका है। अर्थात् D, AB का मध्य बिन्दु है जो ∆ABC को दो भागों में विभाजित करता है अर्थात्

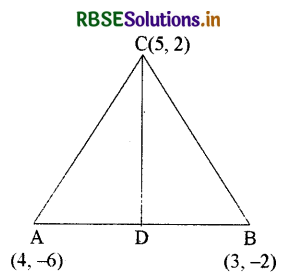
∆ADC में,
x₁ = 4, x₂ = 3.5, x₃ = 5
y₁ = -6, y₂ = -4, y₃ = 2
∆ADC का क्षेत्रफल = \(\frac{1}{2}\) [x₁(y₂ - y₃) + x₂ (y₃ - y₁) + x₃(y₁ - y₂)]
= \(\frac{1}{2}\) [4(-4 - 2) + 3.5(2 + 6) + 5(-6 + 4)]
= \(\frac{1}{2}\) [-24 + 28 - 10]
= \(\frac{1}{2}\) [-34 + 28]
= \(\frac{1}{2}\) [-6]
= -3
= 3 वर्ग मात्रक (∵ क्षेत्रफल ऋणात्मक नहीं हो सकता)
∆CDB में,
x₁ = 5, x₂ = 3.5, x₃ = 3
y₁ = 2, y₂ = -4, y₃ = -2
∆CDB का क्षेत्रफल = \(\frac{1}{2}\) [x₁(y₂ - y₃) + x₂ (y₃ - y₁) + x₃(y₁ - y₂)]
= \(\frac{1}{2}\) [5(-4 + 2) + 3.5(-2 - 2) + 3(2 + 4)]
= \(\frac{1}{2}\) [-10 - 14 + 18]
= \(\frac{1}{2}\) [-24 + 18]
= \(\frac{1}{2}\) [-6]
= -3
= 3 वर्ग मात्रक (∵ क्षेत्रफल ऋणात्मक नहीं हो सकता)
अतः स्पष्ट है कि ∆ADC का क्षेत्रफल = ∆CDB का क्षेत्रफल = 3 वर्ग मात्रक
अतः त्रिभुज की माध्यिका इसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है।