RBSE Solutions for Class 10 Maths Chapter 7 निर्देशांक ज्यामिति Ex 7.1

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 7 निर्देशांक ज्यामिति Ex 7.1 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 7 निर्देशांक ज्यामिति Ex 7.1

Exercise 7.1 Class 10 In Hindi प्रश्न 1.
बिन्दुओं के निम्नलिखित युग्मों के बीच की दूरियाँ ज्ञात कीजिए :
(i) (2, 3), (4, 1)
(ii) (-5, 7), (-1, 3)
(iii) (a, b), (-a, -b)
हल-
(i) प्रश्नानुसार बिन्दु हैं : (2, 3), (4, 1)
अभीष्ट दूरी = \(\sqrt{(4-2)^{2}+(1-3)^{2}}\)
= \(\sqrt{4+4}\)
= √8 
= 2√2 मात्रक

(ii) प्रश्नानुसार बिन्दु हैं : (-5, 7), (-1, 3)
अभीष्ट दूरी = \(\sqrt{(-1+5)^{2}+(3-7)^{2}}\)
= \(\sqrt{16+16}\)
= √32 
= 4√2 मात्रक

(iii) प्रश्नानुसार बिन्दु हैं : (a, b), (-a, -b)
अभीष्ट दूरी = \(\sqrt{(-a-a)^{2}+(-b-b)^{2}}\)
= \(\sqrt{(-2 a)^{2}+(-2 b)^{2}}\)
= \(\sqrt{4 a^{2}+4 b^{2}}\)
= 2\( \sqrt{a^{2}+b^{2}}\) मात्रक

Class 10th Math Chapter 7.1 In Hindi प्रश्न 2.
बिन्दुओं (0, 0) और (36, 15) के बीच की दूरी ज्ञात कीजिए। क्या अब आप अनुच्छेद 7.2 में दिए दोनों शहरों A और B के बीच की दूरी ज्ञात कर सकते हैं?
हल-
प्रश्नानुसार बिन्दु हैं : A(0, 0) और B(36, 15)
दूरी AB = \(\sqrt{(0-36)^{2}+(0-15)^{2}}\)
= \(\sqrt{1296+225}\)
= √1521 
= 39 मात्रक

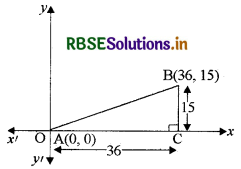
अनुच्छेद 7.2 के अनुसार,
विभिन्न बिन्दु A(0, 0) और B(36, 15) आकृति में दिखाए अनुसार खींची तथा
BC ⊥ X-अक्ष पर खींचिए।
अब, समकोण ∆ACB में,
AB = \(\sqrt{A C^{2}+B C^{2}}\)
= \(\sqrt{(36)^{2}+(15)^{2}}\)
= \(\sqrt{1296+225}\)
= √1521
= 39 मात्रक
अतः दोनों शहरों A और B के बीच की अभीष्ट दूरी 39 km है।

Class 10 Maths Chapter 7 Exercise 7.1 In Hindi प्रश्न 3.
निर्धारित कीजिए कि क्या बिन्दु (1, 5), (2, 3) और (-2, -11) संरेखी हैं।
हल-
प्रश्नानुसार बिन्दु हैं : A(1, 5), B(2, 3) और (-2, -11)

उपर्युक्त दूरियों से, यह स्पष्ट है कि किन्हीं दो का योगफल तीसरे के बराबर नहीं है। अतः, दिए गए बिन्दु संरेखी नहीं हैं।

Class 10 Maths 7.1 Solutions In Hindi प्रश्न 4.
जाँच कीजिए कि क्या बिन्दु (5, -2); (6, 4) और (7, -2) एक समद्विबाहु त्रिभुज के शीर्ष हैं।
हल-
प्रश्नानुसार बिन्दु हैं : A(5, -2), B(6, 4) और C(7, -2)

उपर्युक्त दूरियों से स्पष्ट है कि
AB = BC = √37 मात्रक
∴ दिए गए बिन्दु समद्विबाहु त्रिभुज के शीर्ष हैं।

Class 10 Maths Chapter 7 Exercise 7.1 In Hindi Medium प्रश्न 5.
किसी कक्षा में, चार मित्र बिन्दुओं A, B, C और D पर बैठे हुए हैं, जैसा कि आकृति में दर्शाया गया है। चंपा और चमेली कक्षा के अन्दर आती हैं और कुछ मिनट तक देखने के बाद, चंपा, चमेली से पूछती है, 'क्या तुम नहीं सोचती हो कि ABCD एक वर्ग है?' चमेली इससे सहमत नहीं है। दूरी सूत्र का प्रयोग करके बताइए कि इनमें कौन सही है।

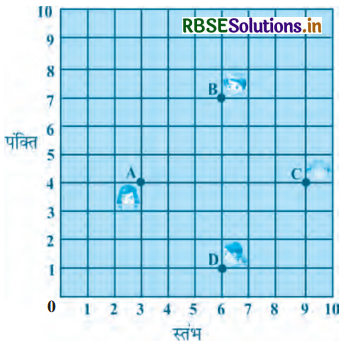
हल-
दी गई आकृति में दिए गए बिन्दुओं के शीर्ष हैं :
A(3, 4), B(6, 7), C(9, 4) और D(6, 1)

उपर्युक्त दूरियों से यह स्पष्ट है कि
AB = BC = CD = DA = 3√2 मात्रक और AC = BD = 6 मात्रक
∴ ABCD एक वर्ग बनाता है तथा चंपा का कथन सही है।

10th Class Maths Chapter 7 Exercise 7.1 In Hindi प्रश्न 6.
निम्नलिखित बिन्दुओं द्वारा बनने वाले चतुर्भुज का प्रकार (यदि कोई है तो) बताइए तथा अपने उत्तर के लिए कारण भी दीजिए :
(i) (-1, -2), (1, 0), (-1, 2), (-3, 0)
हल-
प्रश्नानुसार बिन्दु हैं :
A(-1, -2), B(1, 0), C(-1, 2) और D(-3, 0)

उपर्युक्त से यह स्पष्ट है कि
AB = BC = CD = DA = 8 = 2√2 मात्रक और AC = BD = 4 मात्रक
अतः, दिया गया चतुर्भुज ABCD एक वर्ग है।

(ii) (-3, 5), (3, 1), (0, 3), (-1, -4)
हल-
प्रश्नानुसार बिन्दुओं : A(-3, 5), B(3, 1), C(0, 3) और D(-1, -4)

अब, BC + CA = √13 + √13
= 2√13 
= AB
∴ A, B और C संरेखी हैं तो A, B, C और D चतुर्भुज नहीं बनाते हैं।

(iii) (4, 5), (7, 6), (4, 3), (1, 2)
हल-
प्रश्नानुसार बिन्दुओं : A(4, 5), B(7, 6), C(4, 3) और D(1, 2)

उपर्युक्त से यह स्पष्ट है कि
AB = CD और BC = DA और AC ≠ BD
अर्थात् सम्मुख भुजाएँ बराबर हैं, परन्तु उनके विकर्ण बराबर नहीं हैं।
अतः दिया गया चतुर्भुज ABCD एक समान्तर चतुर्भुज है।

Class 10 Maths Chapter 7.1 In Hindi प्रश्न 7.
x-अक्ष पर वह बिन्दु ज्ञात कीजिए जो (2, -5) और (-2, 9) से समदूरस्थ है।
हल-
माना कि x-अक्ष पर अभीष्ट बिन्दु P(x, 0) और दिए गए बिन्दु हैं A(2, -5) और B(-2, 9)
प्रश्नानुसार, PA = PB
या (PA)² = (PB)²
या (2 - x)² + (-5 - 0)² = (-2 - x)² + (9 - 0)²
या 4 + x² - 4x + 25 = 4 + x² + 4x + 81
या -8x = 56
या x = -7
अतः x-अक्ष पर अभीष्ट बिन्दु (-7, 0) है।

प्रश्न 8.
y का वह मान ज्ञात कीजिए जिसके लिए बिन्दु P(2, -3) और Q(10, y) के बीच की दूरी 10 मात्रक है।
हल-
प्रश्नानुसार बिन्दु हैं : P(2, -3) और Q(10, y)
PQ = \(\sqrt{(10-2)^{2}+(y+3)^{2}}\)
= \(\sqrt{64+y^{2}+9+6 y}\)
= \(\sqrt{y^{2}+6 y+73}\)
पुनः प्रश्नानुसार,
PQ = 10
या \(\sqrt{y^{2}+6 y+73}\) = 10
दोनों पक्षों का वर्ग करने पर या
या y² + 6y + 73 = 100
या y² + 6y - 27 = 0
या y² + 9y - 3y - 27 = 0
या y(y + 9) - 3(y + 9) = 0
या (y + 9) (y - 3)= 0
y + 9= 0 या y - 3 = 0
y = -9 या y = 3
अतः y = -9 और 3

Class 10 Math 7.1 In Hindi प्रश्न 9.
यदि Q(0, 1) बिन्दुओं P(5, -3) और R(x, 6) से समदूरस्थ है, तोx का मान ज्ञात कीजिए। दूरियाँ QR और PR भी ज्ञात कीजिए।
हल-
प्रश्नानुसार बिन्दु हैं : Q(0, 1); P(5, -3) और R(x, 6)
QP = \(\sqrt{(5-0)^{2}+(-3-1)^{2}}\)
= \(\sqrt{25+16}\)
=\( \sqrt{41}\)
और QR = \(\sqrt{(x-0)^{2}+(6-1)^{2}}\)
= \(\sqrt{x^{2}+25}\)
पुनः प्रश्नानुसार,
QP = QR या
\(\sqrt{41} = \sqrt{x^{2}+25}\)
दोनों पक्षों का वर्ग करने पर
41 = x² + 25
या x² = 16
या x = ±√16 = ±4
इस प्रकार से R के निर्देशांक होंगे R(4, 6) या R(-4, 6)
जब x = 4 तो R(4, 6)
QR = \(\sqrt{(4-0)^{2}+(6-1)^{2}}\)

अतः x = ±4, QR = √41 और PR = 9√2 या √162

Class 10 Maths Ex 7.1 In Hindi प्रश्न 10.
x और y में एक ऐसा सम्बन्ध ज्ञात कीजिए कि बिन्दु (x, y) बिन्दुओं (3, 6) और (-3, 4) से समदूरस्थ हो।
हल-
माना कि अभीष्ट बिन्दु P(x, y) है।
दिए गए बिन्दु हैं : A(3, 6) और B(-3, 4)

दोनों पक्षों का वर्ग करने पर,
या x² + y² - 6x - 12y + 45 = x² + y² + 6x - 8y + 25
या -12x - 4y + 20 = 0 [(-4) से दोनों पक्षों में भाग देने पर]
या 3x + y - 5 = 0
यही अभीष्ट सम्बन्ध है।