RBSE Solutions for Class 10 Maths Chapter 6 त्रिभुज Ex 6.6

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 6 त्रिभुज Ex 6.6 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 6 त्रिभुज Ex 6.6

प्रश्न 1.
दी गयी आकृति में, PS कोण ∠QPR का समद्विभाजक है। सिद्ध कीजिए कि \(\frac{\mathrm{QS}}{\mathrm{SR}}=\frac{\mathrm{PQ}}{\mathrm{PR}}\) है।

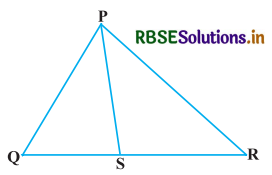
हल-
दिया है : एक ΔPQR है जिसमें PS कोण ∠QPR का समद्विभाजक है अर्थात् ∠1 = ∠2 है।
सिद्ध करना है : \(\frac{Q S}{S R}=\frac{P Q}{P R}\)

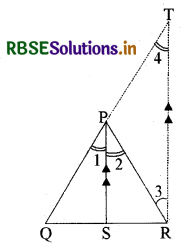
रचना : R में से एक रेखा PS के समान्तर खींचिए जो QP को बढ़ाने पर T पर मिलती है।
उपपत्ति : ΔQRT में, PS || TR
∠2 = ∠3 (एकान्तर कोण)
∠1 = ∠4 (संगत कोण)
परन्तु ∠1 = ∠2 (दिया है)
∴ ∠3 = ∠4
ΔPRT में,
∠3 = ∠4 (सिद्ध कर चुके हैं)
PT = PR [∵ समान भुजाओं के सम्मुख कोण समान होते हैं।]
ΔQRT में, PS || TR
∴ \(\frac{Q P}{P T}=\frac{Q S}{S R}\) [आधारभूत समानुपातिकता प्रमेय से]
\(\frac{Q P}{P R}=\frac{Q S}{S R}\) [∵ PT = PR]
\(\frac{\mathrm{PQ}}{\mathrm{PR}}=\frac{\mathrm{QS}}{\mathrm{SR}}\) (इतिसिद्धम)

प्रश्न 2.
दी गयी आकृति में, D त्रिभुज ABC के कर्ण AC पर स्थित एक बिन्दु है जबकि BD ⊥ AC तथा DM ⊥ BC और DN ⊥ AB, सिद्ध कीजिए कि-
(i) DM² = DN . MC
(ii) DN² = DM . AN

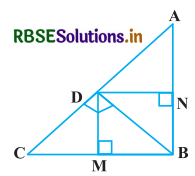
हल-
दिया है : समकोण ΔABC में, DM ⊥ BC, DN ⊥ AB है।
सिद्ध करना है :
(i) DM² = DN . MC
(ii) DN² = DM . AN
उपपत्ति : BD ⊥ AC (दिया है)
∠BDC = 90°
∠BDM + ∠MDC = 90° ......(i)

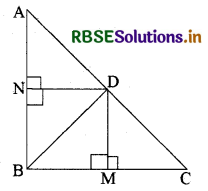
ΔDMC में,
∠DMC = 90° [∵ DM ⊥ BC (दिया है)]
∠C + ∠MDC = 90° ......(ii)
(i) और (ii) से,
∠BDM + ∠MDC = ∠C + ∠MDC
∠BDM = ∠C
अब ΔBMD और ΔMDC में,
∠BDM = ∠C (सिद्ध कर चुके हैं)
∠BMD = ∠MDC (प्रत्येक 90°)
(i) ∴ ΔBMD ~ ΔMDC [AA समरूपता कसौटी से]
\(\frac{\mathrm{DM}}{\mathrm{BM}}=\frac{\mathrm{MC}}{\mathrm{DM}}\)
या DM² = BM × MC
या DM² = DN . MC [∵ BM = DM] (इतिसिद्धम्)
(ii) इसी प्रकार ΔNDA ~ ΔNBD
\(\frac{\mathrm{DN}}{\mathrm{BN}}=\frac{\mathrm{AN}}{\mathrm{DN}}\)
या DN² = BN × AN
या DN² = DM . AN (इतिसिद्धम्)

प्रश्न 3.
दी गयी आकृति में ABC एक त्रिभुज है जिसमें ∠ABC > 90° है तथा AD ⊥ CB है। सिद्ध कीजिए कि AC² = AB² + BC² + 2BC . BD है।

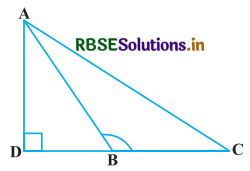
हल-
दिया है : ΔABC में, AD ⊥ BC जब BC को बढ़ाया जाता है।
∠ABC > 90° है।
सिद्ध करना है : AC² = AB² + BC² + 2BC . BD

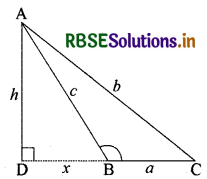
माना कि BC = a, CA = b, AB = c, AD = h और BD = x
समकोण त्रिभुज ΔADC में,
पाइथागोरस प्रमेय से, AC² = CD² + AD²
अर्थात् b² = (x + a)² + h² ......(i)
समकोण त्रिभुज ΔADB में,
AB² = DB² + AD²
c² = x² + h² ......(ii)
समीकरण (i) में से (ii) को घटाने पर
b² - c² = (x + a)² + h² - x² - h²
⇒ b² - c² = x² + 2ax + a² + h² - x² - h²
⇒ b² - c² = a² + 2ax
⇒ b² = c² + a² + 2ax
अतः AC² = AB² + BC² + 2BC . BD (इतिसिद्धम्)

प्रश्न 4.
दी गयी आकृति में, ABC एक त्रिभुज है जिसमें ∠ABC < 90° है तथा AD ⊥ BC है। सिद्ध कीजिए कि AC² = AB² + BC² - 2BC . BD है।

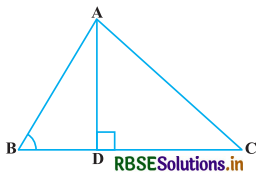
हल-
दिया है : एक ΔABC जिसमें ∠ABC < 90° तथा AD ⊥ BC है।
सिद्ध करना है : AC² = AB² + BC² - 2BC . BD
उपपत्ति : ΔADC एक समकोण त्रिभुज है जिसमें D पर समकोण है।
AC² = CD² + DA² .......(i) (पाइथागोरस प्रमेय से)
साथ ही ΔADB समकोण Δ है D पर समकोण है।
AB² = AD² + DB² .......(ii)
(i) से AC² = AD² + (CB - BD)²
या AC² = AD² + CB² + BD² - 2CB × BD
या AC² = (BD² + AD²) + CB² - 2CB × BD
या AC² = AB² + BC² - 2BC × BD [(ii) के प्रयोग से]
(इतिसिद्धम्)

प्रश्न 5.
दी गयी आकृति में, AD त्रिभुज ABC की एक माध्यिका है तथा AM ⊥ BC है। सिद्ध कीजिए कि
(i) AC² = AD² + BC . DM +\( \left(\frac{B C}{2}\right)^{2}\)
(ii) AB² = AD² - BC . DM + \(\left(\frac{B C}{2}\right)^{2}\)
(iii) AC² + AB² = 2AD² + \(\frac{1}{2}\)BC²

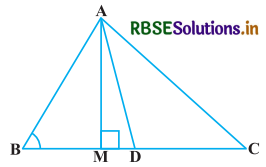
हल-
दिया है : ΔABC में, AM ⊥ BC, AD, ΔABC की एक माध्यिका है।
सिद्ध करना है :
(i) AC² = AD² + BC . DM + \(\left(\frac{B C}{2}\right)^{2}\)
(ii) AB² = AD² - BC . DM + \(\left(\frac{B C}{2}\right)^{2}\)
(iii) AC² + AB² = 2AD² + \(\frac{1}{2}\)BC²
उपपत्ति : ΔAMC में,
AC² = AM² + MC²
AC² = AM² + (MD + DC)²
AC² = AM² + MD² + DC² + 2MD × DC
AC² = (AM² + MD²) + \(\left(\frac{B C}{2}\right)^{2}\) + 2 . MD \(\left(\frac{B C}{2}\right)\) [∵ AD एक माध्यिका है।]
AC² = AD² + BC × MD + \(\left(\frac{\mathrm{BC}}{2}\right)^{2}\)
∴ AC² = AD² + BC . MD + \(\left(\frac{\mathrm{BC}}{2}\right)^{2}\) (इतिसिद्धम्) .....(i)
(ii) समकोण त्रिभुज AMB में,
AB² = AM² + BM²
= AM² + (BD - MD)²
= AM² + BD² + MD² - 2BD × MD

प्रश्न 6.
सिद्ध कीजिए कि एक समान्तर चतुर्भुज के विकर्णों के वर्गों का योग उसकी भुजाओं के वर्गों के. योग के बराबर होता है।
हल-

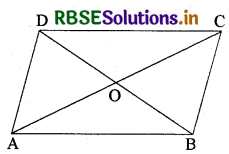
दिया है : माना कि ABCD एक समान्तर चतुर्भुज है जिसमें विकर्ण AC और BD परस्पर बिन्दु O पर प्रतिच्छेद करते हैं।
सिद्ध करना है: AB² + BC² + CD² + DA² = AC² + BD²
उपपत्ति : समान्तर चतुर्भुज के विकर्ण एक-दूसरे को परस्पर विभाजित करते हैं।
अर्थात् OB और OD क्रमशः त्रिभुज ABC और ADC की माध्यिका है।
∴ AB² + BC² = 2BO² + \(\frac{1}{2}\)AC² .......(i)
और AD² + CD² = 2DO² + \(\frac{1}{2}\)AC² ......(i)
(i) और (ii) को जोड़ने पर,
AB² + BC² + AD² + CD² = 2(BO² + DO²) + \(\frac{1}{2}\) (AC² + AC²)
AB² + BC² + AD² + CD² = 2(\(\frac{1}{4}\)BD² + \(\frac{1}{4}\)BD²) + AC²
[∵ BO = \(\frac{1}{2}\) BD, OD = \(\frac{1}{2}\) BD]
AB² + BC² = 2 × \(\frac{1}{2}\) BD² + AC²
∴ AB² + BC² + AD² + CD² = BD² + AC²
अर्थात् एक समान्तर चतुर्भुज के विकर्णों के वर्गों का योग उसकी भुजाओं के वर्गों के योग के बराबर होता है।
(इतिसिद्धम्)

प्रश्न 7.
दी गयी आकृति में, एक वृत्त की दो जीवाएँ AB और CD परस्पर बिन्दु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ΔAPC ~ ΔDPB
(ii) AP . PB = CP . DP

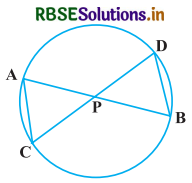
हल-
दिया है : एक वृत्त की दो जीवाएँ AB और CD परस्पर बिन्दु P पर प्रतिच्छेद करती हैं।

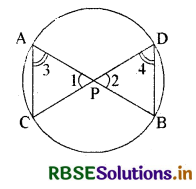
सिद्ध करना है :
(i) ΔAPC ~ ΔDPB
(ii) AP . PB = CP . DP
उपपत्ति : (i) ΔAPC और ΔDPB में,
∠1 = ∠2 (शीर्षाभिमुख कोण)
∠3 = ∠4 (एक ही वृत्तखण्ड के कोण)
∴ ΔAPC ~ ΔDPB [AA समरूपता कसौटी से] (इतिसिद्धम्)
(ii) ΔAPC ~ ΔDPB (सिद्ध कर चुके हैं)
अतः \(\frac{A P}{D P}=\frac{P C}{P B}\) यदि दो त्रिभज समरूप हों तो उनकी संगत भुजायें समानुपाती होती हैं।
AP . PB = PC . DP (इतिसिद्धम्)

प्रश्न 8.
दी गयी आकृति में, एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिन्दु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ΔPAC ~ ΔPDB
(ii) PA . PB = PC . PD

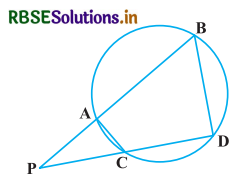
हल-
दिया है : एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिन्दु P पर प्रतिच्छेद करती हैं।
सिद्ध करना है :
(i) ΔPAC ~ ΔPDB
(ii) PA . PB = PC . PD

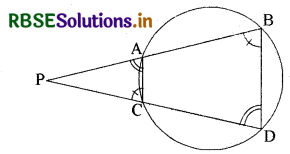
उपपत्ति : (i) ΔPAC और ΔPDB से,
∠P = ∠P (उभयनिष्ठ कोण)
∠PAC = ∠PDB (∵ चक्रीय चतुर्भुज का बाह्य कोण अन्तः सम्मुख कोण के बराबर होता है।)
∴ ΔPAC ~ ΔPDB [AA समरूपता कसौटी से] (इतिसिद्धम्)
(ii) ΔPAC ~ ΔPDB (ऊपर सिद्ध किया है)
∴ \(\frac{\mathrm{PA}}{\mathrm{PD}}=\frac{\mathrm{PC}}{\mathrm{PB}}\) यदि दो Δ समरूप हैं तो उनकी संगत भुजायें समानुपाती होती हैं।
∴ PA × PB = PC × PD (इतिसिद्धम्)

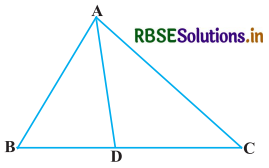
प्रश्न 9.
दी गयी आकृति में, त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि \(\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{AB}}{\mathrm{AC}}\) है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।

हल-
दिया है : ΔABC में, भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि \(\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{AB}}{\mathrm{AC}}\)
सिद्ध करना है : AD, कोण ∠BAC का समद्विभाजक है।
अर्थात् ∠1 = ∠2
रचना : C में से CE || DA खींचिए जो BA को बढ़ाने पर E पर मिले।
उपपत्ति : ΔBCE में,
AD || CE .....(रचना से)

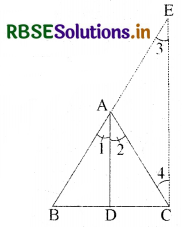
आधारभूत समानुपातिकता प्रमेय से,
\(\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{AB}}{\mathrm{AE}}\)
परन्तु \(\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{AB}}{\mathrm{AC}}\)
∴ \(\frac{\mathrm{AB}}{\mathrm{AE}}=\frac{\mathrm{AB}}{\mathrm{AC}}\)
⇒ AE = AC
ΔACE में, AE = AC
⇒ ∠3 = ∠4 ......(बराबर भुजाओं के सम्मुख कोण)
चूँकि CE || DA और BAE इन्हें प्रतिच्छेद करती है तब
∠2 = ∠4 ......(एकान्तर कोण)
तथा CE || DA और BAE उन्हें प्रतिच्छेद करती है,
∠1 = ∠3 .......(संगत कोण)
इस प्रकार, ∠3 = ∠4
⇒ ∠4 = ∠1
∠3 = ∠1
परन्तु ∠4 = ∠2
⇒ ∠1 = ∠2
AD, ∠BAC को समद्विभाजित करता है। (इतिसिद्धम्)

प्रश्न 10.
नाज़िमा एक नदी की धारा में मछलियाँ पकड़ रही है। उसकी मछली पकड़ने वाली छड़ का सिरा पानी की सतह से 1.8 m ऊपर है तथा डोरी के निचले सिरे से लगा कांटा पानी की सतह पर इस प्रकार स्थित है कि उसकी नाज़िमा से दूरी 3.6 m है और छड़ के सिरे के ठीक नीचे पानी की सतह पर स्थित बिन्दु से उसकी दूरी 2.4 m है। यह मानते हुए कि उसकी डोरी (उसकी छड़ के सिरे से काँटे तक) तनी हुई है, उसने कितनी डोरी बाहर निकाली हुई है (देखिए आकृति )? यदि वह डोरी को 5 cm/s की दर से अन्दर खींचे, तो 12 सेकण्ड के बाद नाजिमा की काँटे से क्षैतिज दूरी कितनी होगी?

हल-
समकोण त्रिभुज ABC में,
AB = 1.8 m, BC = 2.4 m, ∠B = 90°
पाइथागोरस प्रमेय से,
AC² = AB² + BC²
⇒ AC² = (1.8)² + (2.4)²
⇒ AC² = 3.24 + 5.76 = 9
⇒ AC² = (3)²
⇒ AC = 3 m
अब नाज़िमा डोरी को 5 cm/s की दर से अन्दर खींचे, तो डोरी की लम्बाई कम होती है।
= 5 × 12
= 60 cm
= 0.6 m; 12 सेकण्ड में,
माना कि 12 सेकण्ड के बाद काँटे की स्थिति D है।
∴ AD = AC - (12 सेकण्ड में तय दूरी)
= (3 - 0.6) m
= 2.4 m
अब, समकोण त्रिभुज ∆ABD में,
पाइथागोरस प्रमेय से,
AD² = AB² + BD²
⇒ (2.4)² = (1.8)² + BD²
⇒ BD² = 5.76 - 3.24
⇒ BD² = 2.52 m
⇒ BD = 1.587 m ~ 1.59 m
∴ नाज़िमा द्वारा तय की गई क्षैतिज दूरी = BD + 1.2 m
= (1.59 + 1.2) m
= 2.79 m
अतः डोरी की लम्बाई और नाजिमा द्वारा तय की गई दूरी 3 m और 2.79 m है।