RBSE Solutions for Class 10 Maths Chapter 6 त्रिभुज Ex 6.4

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 6 त्रिभुज Ex 6.4 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 6 त्रिभुज Ex 6.4

प्रश्न 1.
मान लीजिए ∆ABC ~ ∆DEF है और इनके क्षेत्रफल क्रमशः 64 cm² और 121 cm² हैं। यदि EF = 15.4 cm हो, तो BC ज्ञात कीजिए।
हल-
∆ABC ~ ∆DEF,
∆ABC का क्षेत्रफल = 64 cm² और ∆DEF का क्षेत्रफल = 121 cm² और EF = 15.4 cm है।

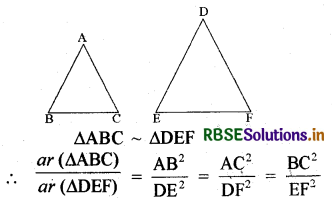
[∵ हम जानते हैं कि यदि दो त्रिभुज समरूप हों तो उनके क्षेत्रफलों का अनुपात संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।]

प्रश्न 2.
एक समलम्ब ABCD जिसमें AB || DC है, के विकर्ण परस्पर बिन्दु O पर प्रतिच्छेद करते हैं। यदि AB = 2CD हो, तो त्रिभुजों AOB और COD के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल-
ABCD एक समलम्ब है जिसमें AB || DC है, के विकर्ण AC और BD परस्पर बिन्दु O पर प्रतिच्छेद करते हैं। AB = 2CD है।

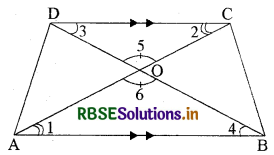
अब, ∆AOB और ∆COD में,
∠1 = ∠2 (एकान्तर कोण)
∠3 = ∠4 (एकान्तर कोण)
∠5 = ∠6 (शीर्षाभिमुख कोण)
∴ ∆AOB ~ ∆COD

∴ वांछित ar ∆AOB और ar ∆COD का अनुपात = 4 : 1

प्रश्न 3.
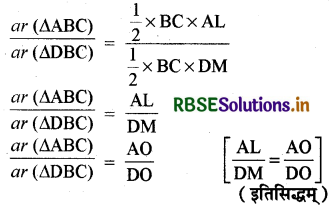
आकृति में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए हैं। यदि AD, BC को O पर प्रतिच्छेद करे, तो दर्शाइए कि \(\frac{\operatorname{ar}(\mathrm{ABC})}{\operatorname{ar}(\mathrm{DBC})}=\frac{\mathrm{AO}}{\mathrm{DO}}\) है।

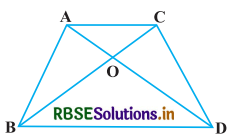
हल-
दिया है : ∆ABC और ∆DBC एक ही आधार BC पर स्थित बने हुए दो त्रिभुज हैं। AD, BC को O पर प्रतिच्छेद करता है।

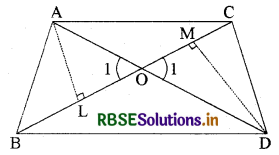
सिद्ध करना है : \(\frac{\operatorname{ar}(\mathrm{ABC})}{\operatorname{ar}(\mathrm{DBC})}=\frac{\mathrm{AO}}{\mathrm{DO}}\)
रचना : AL ⊥ BC, DM ⊥ BC खींचिए।
उपपत्ति : ∆ALO और ∆DMO में,
∠1 = ∠2 (शीर्षाभिमुख कोण)
∠L = ∠M (प्रत्येक 90°)
∴ ∆ALO ~ ∆DMO [AA समरूपता कसौटी]
∴ \(\frac{\mathrm{AL}}{\mathrm{DM}}=\frac{\mathrm{AO}}{\mathrm{DO}}\) .......(i)
[∵ यदि दो त्रिभुज समरूप हों, तो संगत भुजाएँ समानुपाती होती हैं।]

प्रश्न 4.
यदि दो समरूप त्रिभुजों के क्षेत्रफल बराबर हों तो सिद्ध कीजिए कि वे त्रिभुज सर्वांगसम होते हैं।
हल-
दिया है : दो त्रिभुज ABC और DEF समरूप हैं और क्षेत्रफल में बराबर हैं।
सिद्ध करना है : ∆ABC ≅ ∆DEF

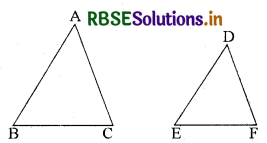
उपपत्ति : चूँकि ∆ABC ~ ∆DEF,
∴ \(\frac{\operatorname{ar}(\triangle \mathrm{ABC})}{\operatorname{ar}(\triangle \mathrm{DEF})}=\frac{\mathrm{BC}^{2}}{\mathrm{EF}^{2}}\)
⇒ \(\frac{\mathrm{BC}^{2}}{\mathrm{EF}^{2}}\) = 1 [∵ ar(∆ABC) = ar(∆DEF)]
⇒ BC² = EF²
⇒ BC = EF
साथ ही, चूँकि ∆ABC ~ ∆DEF, इसलिए वे समकोणिक हैं।
और, ∠B = ∠E और ∠C = ∠F
अब त्रिभुजों ABC और DEF में
∠B = ∠E, ∠C = ∠F और BC = EF
∴ ∆ABC ≅ ∆DEF (ASA सर्वांगसमता प्रमेय)
(इतिसिद्धम्)

प्रश्न 5.
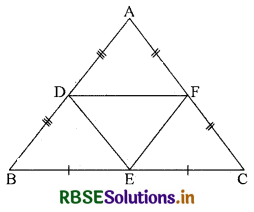
एक त्रिभुज ABC की भुजाओं AB, BC और CA के मध्य-बिन्दु क्रमशः D, E और F हैं। ∆DEF और ∆ABC के क्षेत्रफल का अनुपात ज्ञात कीजिए।
हल-
दिया है : एक ∆ABC की भुजाओं AB, BC और CA के मध्य-बिन्दु क्रमशः D, E और F हैं।
अभीष्ट : ar(∆DEF) : ar(∆ABC) ज्ञात करना है।
उपपत्ति : दिया गया है कि D और E भुजा AB और BC के मध्य बिन्दु ∆ABC में है।
∴ DE || AC
⇒ DE || FC .......(ii)

इसी तरह से D और F भुजा AB और AC के मध्य बिन्दु ∆ABC में है।
∴ DF || BC
⇒ DF || EC ......(ii)
(i) तथा (ii) से स्पष्ट है कि DECF एक समान्तर चतुर्भुज है।
इसी प्रकार से ADEF एक समान्तर चतुर्भुज है।
अब ∆DEF और ∆ABC में
∠DEF = ∠A (समान्तर चतुर्भुज ADEF से)
और ∠EDF = ZC (समान्तर चतुर्भुज DECF से)
∴ AA समरूपता से
∆DEF ~ ∆ABC

∴ क्षेत्रफल (∆DEF) : क्षेत्रफल (∆ABC) = 1 : 4

प्रश्न 6.
सिद्ध कीजिए कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत माध्यिकाओं के अनुपात का वर्ग होता है।
हल-
दिया है : दो समरूप त्रिभुज ABC तथा DEF है।
AP और DM क्रमशः भुजाओं BC और EF की माध्यिकाएँ हैं।

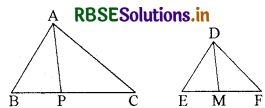
सिद्ध करना है : \(\frac{\operatorname{ar}(\triangle \mathrm{ABC})}{\operatorname{ar}(\triangle \mathrm{DEF})}=\frac{\mathrm{AP}^{2}}{\mathrm{DM}^{2}}\)
उपपत्ति : ∆ABC ~ ∆DEF (दिया है)
∴ \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{2 \mathrm{BP}}{2 \mathrm{EM}}\) [∵ AP और DM माध्यिकाएँ हैं।]
∴ BC = 2BP और EF = 2EM
⇒ \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BP}}{\mathrm{EM}}\) ......(i)
∆ABP और ∆DEM में,
∠B = ∠E [∵ ∆ABC ~ ∆DEF]
\(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BP}}{\mathrm{EM}}\) [(i) में सिद्ध किया है]
∴ ∆ABP ~ ∆DEM [SAS समरूपता कसौटी से]
∴ \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AP}}{\mathrm{DM}}\) ...... (ii)
चूँकि, दो समरूप त्रिभुजों के क्षेत्रफल का अनुपात इनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।
∴ \(\frac{a r(\triangle \mathrm{ABC})}{a r(\triangle \mathrm{DEF})}=\frac{\mathrm{AB}^{2}}{\mathrm{DE}^{2}}=\frac{\mathrm{AP}^{2}}{\mathrm{DM}^{2}}\)
(इतिसिद्धम्)

प्रश्न 7.
सिद्ध कीजिए कि एक वर्ग की किसी भुजा पर बनाए गए समबाहु त्रिभुज का क्षेत्रफल उसी वर्ग के एक विकर्ण पर बनाए गए समबाहु त्रिभुज के क्षेत्रफल का आधा होता है।
हल-
दिया है : ABCD एक वर्ग है। समबाहु ∆ABE वर्ग की भुजा AB पर स्थित है और समबाहु ∆ACF विकर्ण AC पर बना है।

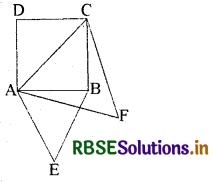
सिद्ध करना है : \(\frac{\operatorname{ar}(\triangle \mathrm{ABE})}{a r(\triangle \mathrm{ACF})}=\frac{1}{2}\)
उपपत्ति : समकोण ∆ABC में,
AB² + BC² = AC² [पाइथागोरस प्रमेय से]
या AB² + AB² = AC² [∵ AB = BC, एक ही वर्ग की भुजाएँ]
या 2AB² = AC² ....... (i)
अब, प्रत्येक ∆ABE और ∆ACF समबाहु हैं इसलिए समकोणिक हैं और इसलिए समरूप हैं।
अर्थात् ∆ABE ~ ∆ACF
यहाँ पहले ∆ की कोई भुजा दूसरे त्रिभुज की किसी भुजा के समान्तर है।
∴ \(\frac{a r(\triangle \mathrm{ABE})}{a r(\triangle \mathrm{ACF})}=\frac{\mathrm{AB}^{2}}{\mathrm{AC}^{2}}\)
[∵ दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी | संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।]
⇒ \(\frac{\mathrm{AB}^{2}}{2 \mathrm{AB}^{2}}=\frac{1}{2}\) [(i) का प्रयोग करने पर]
अत: ∆ABE का क्षेत्रफल = \(\frac{1}{2}\) ∆ACF का क्षेत्रफल
(इंतिसिद्धम्)

सही उत्तर चुनिए और अपने उत्तर का औचित्य दीजिए :

प्रश्न 8.
ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिन्दु है। त्रिभुजों ABC और BDE के क्षेत्रफलों का अनुपात है-
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 1 : 4
हल-
∆ABC और ∆BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिन्दु है।

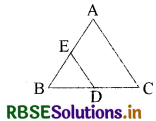
∴ BD = DC = \(\frac{1}{2}\) BC
या BC : BD = 2 : 1
माना किं समबाहु त्रिभुज की भुजा 2a है।
∴ ∆ABC ~ ∆BDE
चूँकि समबाहु त्रिभुज में समान कोण होते हैं।

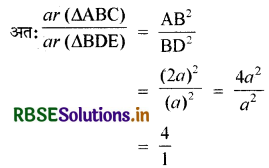
∴ सही विकल्प (C) 4 : 1

प्रश्न 9.
दो समरूप त्रिभुजों की भुजाएँ 4 : 9 के अनुपात में हैं। इन त्रिभुजों के क्षेत्रफलों का अनुपात है :
(A) 2 : 3
(B) 4 : 9
(C) 81 : 16
(D) 16 : 81
हल-

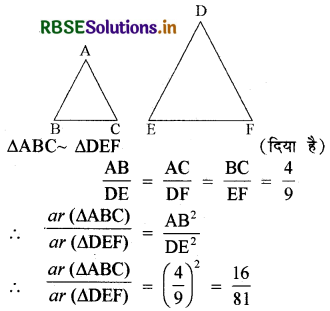
∴ सही विकल्प (D) 16 : 81