RBSE Solutions for Class 10 Maths Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.4

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.4 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.4

प्रश्न 1.
निम्न समीकरणों के युग्म को विलोपन विधि तथा प्रतिस्थापना विधि से हल कीजिये। कौनसी विधि अधिक उपयुक्त है?
(i) x + y = 5 और 2x - 3y = 4
हल-
दिया गया रैखिक समीकरणों का युग्म है :
x + y = 5 ......(1)
और 2x - 3y = 4 .......(2)
विलोपन विधि-
(1) को 2 से गुणा करने पर
2x + 2y = 10 ......(3)
समीकरण (3) में से (2) को घटाने पर
2x + 2y = 10
2x - 3y = 4
या 5y = 6
या y = \(\frac{6}{5}\)
y का यह मान (1) में प्रतिस्थापित करने पर
x + \(\frac{6}{5}\) = 5
या x = 5 - \(\frac{6}{5}\)
या x = \(\frac{19}{5}\)
अतः, x = \(\frac{19}{5}\) और \(\frac{6}{5}\)
प्रतिस्थापन विधि-
(2) से, 2x = 4 + 3y
या x = \(\frac{4+3 y}{2}\) ........(4)
x का यह मान (1) में प्रतिस्थापित करने पर
\(\frac{4+3 y}{2}\) + y = 5
या \(\frac{4+3 y+2 y}{2}\) = 5
या 4 + 5y = 10
या 5y = 10 - 4 = 6
या y = \(\frac{6}{5}\)
y का यह मान (4) में प्रतिस्थापित करने पर

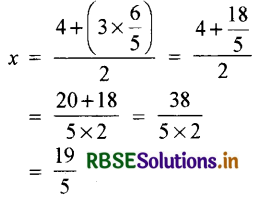
अतः x = \(\frac{19}{5}\) और y = \(\frac{6}{5}\)

(ii) 3x + 4y = 10 और 2x - 2y = 2
हल-
दिया गया रैखिक समीकरण युग्म है :
3x + 4y = 10 ........(1)
और 2x - 2y = 2 ......(2)
विलोपन विधि-
समीकरण (2) को 2 से गुणा करने पर
4x - 4y = 4 ......(3)
समीकरण (3) और (1) को जोड़ने पर
4x - 4y = 4
3x + 4y = 10
7x = 14
या x = 2
x का यह मान (1) में प्रतिस्थापित करने पर
3(2) + 4y = 10
6 + 4y = 10
4y = 10 - 6
4y = 4
y = 1
अतः, x = 2 और y = 1
प्रतिस्थापन विधि-
(2) से, 2x = 2 + 2y
या x = y + 1 .......(3)
x का यह मान (1) में प्रतिस्थापित करने पर ,
3(y + 1) + 4 = 10
या 3y + 3 + 4y = 10
या 7y = 10 - 3 = 7
या 7y = 7
या y = 1
y का यह मान (3) में प्रतिस्थापित करने पर
x = 1 + 1 = 2
अतः, x = 2 और y = 1

(iii) 3x - 5y - 4 = 0 और 9x = 2y + 7
हल-
दिया गया रैखिक समीकरण युग्म है :
3x - 5y - 4 = 0 .......(1)
और 9x = 2y + 7
या 9x - 2y - 7 = 0
विलोपन विधि-
समीकरण (1) को 3 से गुणा करने पर
9x - 15y - 12 = 0 ......(3)
समीकरण (3) में से (2) को घटाने पर
9x - 15y - 12 = 0
9x - 2y - 7 = 0
या -13y - 5 = 0
या -13y = 5
या y = \(-\frac{5}{13}\)
y का यह मान (1) में प्रतिस्थापित करने पर
3x - \(5\left(-\frac{5}{13}\right)\) - 4 = 0
या 3x + \(\frac{25}{13}\) - 4 = 0
या 3x = 4 - \(\frac{25}{13}\)
या 3x = \(\frac{52-25}{13}=\frac{27}{13}\)
या x = \(\frac{27}{13} \times \frac{1}{3}=\frac{9}{13}\)
अतः, x = \(\frac{9}{13}\) और y = \(\frac{-5}{13}\)
प्रतिस्थापन विधि-
(2) से, x = \(\frac{2 y+7}{9}\) .......(4)
x का यह मान (1) में प्रतिस्थापित करने पर

अतः, x = \(\frac{9}{13}\) और y = \(\frac{-5}{13}\)

(iv) \(\frac{x}{2}+\frac{2 y}{3}\) = -1 और x - \(\frac{y}{3}\) = 3
हल-
दिया गया रैखिक समीकरण युग्म है :

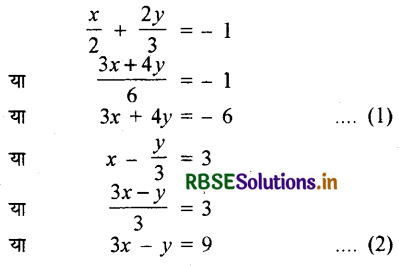
विलोपन विधि-
समीकरण (1) में से (2) को घटाने पर
3x + 4y = -6
3x - y = 9
या 5y = -15
या y = -3
y का यह मान (1) में प्रतिस्थापित करने पर
3x + 4(-3) = -6
या 3x - 12 = - 6
या 3x = -6 + 12
या 3x = 6
या x = 2
अतः, x = 2, y = -3
प्रतिस्थापन विधि-
(2) से, y = 3x - 9 .......(3)
y का यह मान (1) में प्रतिस्थापित करने पर
3x + 4(3x - 9) = -6
या 3x + 12x - 36 = -6
या 15x = -6 + 36
या 15x = 30
या x = 2
x का यह मान (3) में प्रतिस्थापित करने पर
y = 3(2) - 9
= 6 - 9
= -3
अतः, x = 2, y = -3

प्रश्न 2.
निम्न समस्याओं में रैखिक समीकरणों के युग्म बनाइए और उनके हल (यदि उनका अस्तित्व हो) विलोपन विधि से ज्ञात कीजिए।
(i) यदि हम अंश में 1 जोड़ दें तथा हर में से 1 घटा दें, तो भिन्न 1 में बदल जाती है। यदि हर में 1 जोड़ दें, तो यह \(\frac{1}{2}\) हो जाती है। वह भिन्न क्या है?
हल-
माना कि भिन्न का अंश = x
भिन्न का हर = y
∴ अभीष्ट भिन्न = \(\frac{x}{y}\)
पहली शर्त के अनुसार,
\(\frac{x+1}{y+1}\) = 1
या x + 1 = y - 1
या x - y + 2 = 0 .......(1)
दूसरी शर्त के अनुसार,
\(\frac{x}{y+1}=\frac{1}{2}\)
या 2x = y + 1
या 2x - y - 1 = 0 ........(2)
समीकरण (2) में से (1) को घटाने पर
2x - y - 1 = 0
x - y + 2 = 0
या x - 3 = 0
या x = 3
x का यह मान (2) में प्रतिस्थापित करने पर
2 × 3 - y - 1 = 0
या 6 - y - 1 = 0
या 5 - y = 0
या y = 5
अतः, अभीष्ट भिन्न \(\frac{3}{5}\) है।

(ii) पाँच वर्ष पूर्व नूरी की आयु सोनू की आयु की तीन गुनी थी, दस वर्ष पश्चात्, नूरी की आयु सोनू की आयु की दो गुनी हो जाएगी। नूरी और सोनू की आयु कितनी है?
हल-
माना कि नूरी की वर्तमान आयु = x वर्ष
सोनू की वर्तमान आयु = y वर्ष
पाँच वर्ष पूर्व नूरी की आयु = (x - 5) वर्ष
सोनू की आयु = (y - 5) वर्ष
पहली शर्त के अनुसार,
x - 5 = 3(y - 5)
या x - 5 = 3y - 15
या x - 3y + 10 = 0 .......(1)
दस वर्ष पश्चात् नूरी की आयु = (x + 10) वर्ष
सोनू की आयु = (y + 10) वर्ष
दूसरी शर्त के अनुसार,
x + 10 = 2(y + 10)
या x + 10 = 2y + 20
या x - 2y - 10 = 0 ......(2)
समीकरण (1) में से (2) को घटाने पर
x - 3y + 10 = 0
x - 2y - 10 = 0
या -y + 20 = 0
या -y = -20
या y = 20
y का यह मान (2) में प्रतिस्थापित करने पर
x - 2(20) - 0 = 0
या x - 40 - 10 = 0
या x = 50
अतः, नूरी की वर्तमान आयु = 50 वर्ष
सोनू की वर्तमान आयु = 20 वर्ष

(iii) दो अंकों की संख्या के अंकों का योग 9 है। इस संख्या का नौ गुना, संख्या के अंकों को पलटने से बनी संख्या का दो गुना है। वह संख्या ज्ञात कीजिए।
हल-
माना कि इकाई का अंक = x
दहाई का अंक = y
∴ अभीष्ट संख्या = 10y + x
पहली शर्त के अनुसार,
x + y = 9 .......(1)
संख्याएँ पलटने पर
इकाई का अंक = y
दहाई का अंक = x
∴ संख्या = 10x + y
दूसरी शर्त के अनुसार,
9[10y + x] = 2[10x + y]
या 90y + 9x = 20x + 2y
या 90y + 9x - 20x - 2y = 0
या -11x + 88y = 0
या x - 8y = 0 .......(2)
समीकरण (2) में से (1) को घटाने पर
x - 8y = 0
x + y = 9
या -9y = -9
या y = 1
y का यह मान (2) में प्रतिस्थापित करने पर
x - 8 × 1 = 0
या x = 8
अतः, अभीष्ट संख्या = 10y + x
= 10 × 1 + 8
= 18

(iv) मीना 2000 रु. निकालने के लिए एक बैंक गई। उसने खजांची से 50 रु. तथा 100 रु. के नोट देने के लिए कहा। मीना ने कुल 25 नोट प्राप्त किये। ज्ञात कीजिए कि उसने 50 रु. और 100 रु. के कितने-कितने नोट प्राप्त किये।
हल-
माना कि मीना को मिले 50 रु. के नोटों की संख्या = x
साथ ही, मीना को प्राप्त 100 रु. के नोटों की संख्या = y
पहली शर्त के अनुसार,
x + y = 25 ......(1)
दूसरी शर्त के अनुसार,
50x + 100y = 2000
या x + 2y = 40 ......(2)
समीकरण (2) में से (1) को घटाने पर
x + 2y = 40
x + y = 25
या y = 15
y का यह मान (1) में प्रतिस्थापित करने पर
x + 15 = 25
या x = 25 - 15 = 10
अतः, मीना को मिले 50 रु. और 100 के नोटों की संख्या क्रमशः 10 और 15 है।

(v) किराये पर पुस्तकें देने वाले किसी पुस्तकालय का प्रथम तीन दिनों का एक नियत किराया है तथा उसके बाद प्रत्येक अतिरिक्त दिन का अलग किराया है। सरिता ने सात दिनों तक एक पुस्तक रखने के लिए 27 रु. अदा किए, जबकि सूसी ने एक पुस्तक पाँच दिनों तक रखने के 21 रु. अदा किए। नियत किराया तथा प्रत्येक अतिरिक्त दिन का किराया ज्ञात कीजिए।
हल-
माना कि पहले तीन दिन के लिए निश्चित किराया = x रु.
उसके बाद प्रत्येक दिन के लिए अतिरिक्त किराया = y रु.
सरिता की स्थिति में
x + 4y = 27 .......(1)
सूसी की स्थिति में,
x + 2y = 21 .......(2)
समीकरण (1) में से (2) को घटाने पर
x + 4y = 27
x + 2y = 21
या 2y = 6
या y = 3
y का यह मान (2) में प्रतिस्थापित करने पर
x + 2(3) = 21
या x + 6 = 21
या x = 21 - 6 = 15
अतः पहले तीन दिन के लिए नियत किराया और उसके बाद प्रत्येक दिन के लिए अतिरिक्त किराया 15 रु. और 3 रु. है।