RBSE Solutions for Class 10 Maths Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.2

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.2 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.2

प्रश्न 1.
निम्न समस्याओं में रैखिक समीकरणों के युग्म बनाइये और उनके ग्राफीय विधि से हल ज्ञात कीजिए-
(i) कक्षा X के 10 विद्यार्थियों ने एक गणित की पहेली प्रतियोगिता में भाग लिया। यदि लड़कियों की संख्या लड़कों की संख्या से 4 अधिक हो, तो प्रतियोगिता में भाग लिये लड़कों और लड़कियों की संख्या ज्ञात कीजिए।
(ii) 5 पेंसिल और 7 कलमों का कुल मूल्य 50 रु. है, जबकि 7 पेंसिलों और 5 कलमों का कुल मूल्य 46 रु. है। एक पेंसिल का मूल्य और एक कलम का मूल्य ज्ञात कीजिए।
हल-
(i) माना कि
प्रतियोगिता में लड़कों की संख्या = x
और प्रतियोगिता में लड़कियों की संख्या = y
प्रतियोगिता में भाग लेने वाले कल विद्यार्थी = 10
∴ x + y = 10
या x + y - 10 = 0
प्रश्नानुसार y = x + 4
या x = y - 4
अब रैखिक समीकरणों x + y = 10
और x - y + 4 = 0 का आलेख खींचने पर
x + y = 10
x = 10 - y .......(1)
y = 0 को (1) में प्रतिस्थापित करने पर
x = 10 - 0 = 10
y = 7 को (1) में प्रतिस्थापित करने पर
x = 10 - 7 = 3
y = 10 को (1) में प्रतिस्थापित करने पर
x = 10 - 10 = 0

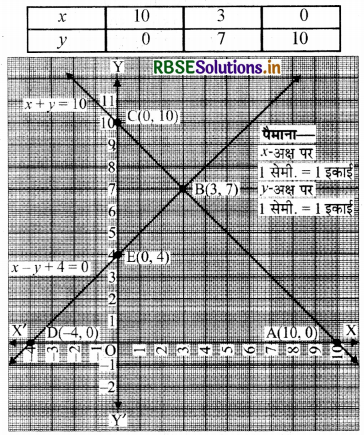
बिन्दुओं A(10, 0), B (3, 7), C (0, 10) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण x + y = 10 का आलेख प्राप्त होता है।
x - y + 4 = 0
या x = y - 4 ......(2)
y = 0 को (2) में प्रतिस्थापित करने पर
x = 0 - 4 = -4
y = 7 को (2) में प्रतिस्थापित करने पर
x = 7 - 4 = 3
y = 4 को (2) में प्रतिस्थापित करने पर
x = 4 - 4 = 0

बिन्दुओं D(-4, 0), B(3, 7), E(0, 4) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण x - y + 4 = 0 का आलेख प्राप्त होता है।
आलेख से यह स्पष्ट है कि दोनों रैखिक समीकरण बिन्दु B(3, 7) पर मिलते
∴ बिन्दु B(3, 7) आलेखीय स्थिति है। अतः प्रतियोगिता में लड़कों की संख्या = 3
प्रतियोगिता में लड़कियों की संख्या = 7

(ii) माना कि 1 पेंसिल का मूल्य = x रु.
और 1 कलम का मूल्य = y रु.
पहली शर्त के अनुसार,
5x + 7y = 50
दूसरी शर्त के अनुसार,
7x + 5y = 46
रैखिक समीकरण युग्म है :
5x + 7y = 50
7x + 5y = 46
अब इन रैखिक समीकरणों का आलेख खींचने पर
5x + 7y = 50
या 5x = 50 - 7y
या x = \(\frac{50-7 y}{5}\) ......(1)
y = 0 को (1) में प्रतिस्थापित करने पर
x = \(\frac{50-7 \times 0}{5}=\frac{50}{5}\) = 10
x = 10
y = 5 को (1) में प्रतिस्थापित करने पर
x = \(\frac{50-7 \times 5}{5}=\frac{50-35}{5}\) = 3
y = 10 को (1) में प्रतिस्थापित करने पर
x = \(\frac{50-7 \times 10}{5} = \frac{50-70}{5}=\frac{-20}{5}\) = -4

बिन्दुओं A(10, 0), B(3, 5), C(-4, 10) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण 5x + 7y = 50 का आलेख प्राप्त होता है।
अब दूसरे समीकरण से
7x + 5y = 46
या 7x = 46 - 5y
या x = \(\frac{46-5 y}{7}\) ....(2)
y = 12 रखने पर,
x = \(\frac{46-5 \times 12}{7} = \frac{46-60}{7}=\frac{-14}{7}\) = -2
y = 5 को (2) में प्रतिस्थापित करने पर
x = \(\frac{46-5 \times 5}{7}=\frac{46-25}{7}\) = 3
y = -2 को (2) में प्रतिस्थापित करने पर
x = \(\frac{46-5 \times(-2)}{7} = \frac{46+10}{7}\) = 8

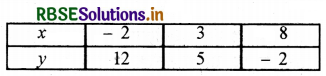
बिन्दुओं E(-2, 12), B(3, 5), F(8, -2) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण 7x + 5y = 46 का आलेख प्राप्त होता है।
आलेख से यह स्पष्ट है कि दोनों रैखिक समीकरण बिन्दु B(3, 5) पर मिलते हैं।
∴ बिन्दु B (3, 5) आलेखीय स्थिति है।
अतः, एक पेंसिल का मूल्य = 3 रु.
एक कलम का मूल्य = 5 रु.

प्रश्न 2.
अनुपाता \(\frac{a_{1}}{a_{2}}, \frac{b_{1}}{b_{2}}\) और \(\frac{c_{1}}{c_{2}}\) ज्ञात कीजिए कि निम्न समीकरण युग्म द्वारा निरूपित रेखाएँ एक बिन्दु पर प्रतिच्छेद करती हैं, समान्तर हैं अथवा संपाती हैं :
(i) 5x - 4y + 8 = 0
7x + 6y - 9 = 0
हल-
दी गई रैखिक समीकरण युग्म है :
5x - 4y + 8 = 0
और 7x + 6y - 9 = 0
उक्त समीकरणों की तुलना a₁x + b₁y + c₁ = 0 तथा a₂x + b₂y + c₂ = 0 से करने पर
यहाँ a₁ = 5, b₁ = -4, c₁ = 8
a₂ = 7, b₂ = 6, c₂ = -9

अतः, दी गई रैखिक समीकरण युग्म एक बिन्दु पर प्रतिच्छेदित करती है।

(ii) 9x + 3y + 12 = 0
18x + 6y + 24 = 0
हल-
दी गई रैखिक समीकरण युग्म है :
9x + 3y + 12 = 0
और 18x + 6y + 24 = 0
उक्त समीकरणों की तुलना a₁x + b₁y + c₁ = 0 तथा a₂x + b₂y + c₂ = 0 से करने पर
यहाँ a₁ = 9, b₁ = 3, c₁ = 12
a₂ = 18, b₂ = 6, c₂ = 24

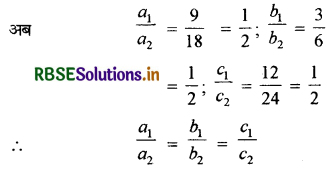
अतः, दी गई समीकरण-युग्म संपाती है।

(iii) 6x - 3y + 10 = 0
2x - y + 9 = 0
हल-
दी गई रैखिक समीकरण-युग्म है :
6x - 3y + 10 = 0
और 2x - y + 9 = 0
उक्त समीकरणों की तुलना a₁x + b₁y + c₁ = 0 तथा a₂x + b₂y + c₂ = 0 से करने पर
यहाँ a₁ = 6, b₁ = -3, c₁ = 10
a₂ = 2, b₂ = -1, c₂ = 9

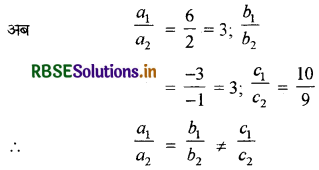
अतः, दी गई रैखिक समीकरण-युग्म एक-दूसरे के समान्तर है।

प्रश्न 3.
अनुपाता \(\frac{a_{1}}{a_{2}}, \frac{b_{1}}{b_{2}}\) और \(\frac{c_{1}}{c_{2}}\) की तुलना कर ज्ञात कीजिए कि निम्न रैखिक समीकरणों के युग्म संगत हैं या असंगत :
(i) 3x + 2y = 5; 2x - 3y = 7
हल-
दी गई रैखिक समीकरण-युग्म है :
3x + 2y = 5
और 2x - 3y = 7
या 3x + 2y - 5 = 0
और 2x - 3y - 7 = 0
यहाँ a₁ = 3, b₁ = 2, c₁ = -5
a₂ = 2, b₂ = -3, c₂ = -7

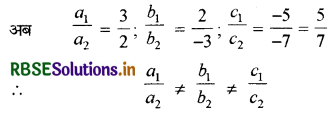
अतः, दी गई रैखिक समीकरण-युग्म संगत है।

(ii) 2x - 3y = 8; 4x - 6y = 9
हल-
दी गई रैखिक समीकरण-युग्म है :
2x - 3y = 8
और 4x - 6y = 9
या 2x - 3y - 8 = 0
4x - 6y - 9 = 0
यहाँ a₁ = 2, b₁ = -3, c₁ = -8
a₂ = 4, b₂ = - 6, c₂ = -9

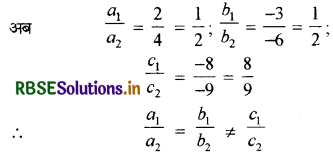
अतः, दी गई रैखिक समीकरण-युग्म असंगत है।

(iii) \(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7; 9x - 10y = 14
हल-
दी गई रैखिक समीकरण-युग्म है :
\(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7
और 9x - 10y = 14
या \(\frac{3}{2}\)x + \(\frac{5}{3}\)y - 7 = 0
और 9x - 10y - 14 = 0
यहाँ a₁ = \(\frac{3}{2}\), b₁ = \(\frac{5}{3}\), c₁ = -7
a₂ = 9, b₂ = -10, c₂ = -14

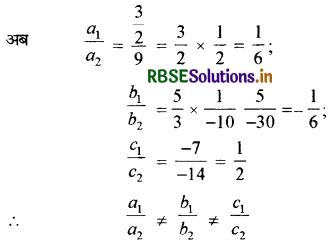
अतः, दी गई रैखिक समीकरण-युग्म संगत है।

(iv) 5x - 3y = 11; -10x + 6y = -22
हल-
दी गई रैखिक समीकरण-युग्म है :
5x - 3y = 11
और -10x + 6y = - 22
या 5x - 3y - 11 = 0
और -10x + 6y + 22 = 0
यहाँ a₁ = 5, b₁ = -3, c₁ = - 11
a₂ = -10, b₂ = 6, c₂ = 22

अतः, दी गई रैखिक समीकरण-युग्म संगत है।

(v) \(\frac{4}{3}\)x + 2y = 8; 2x + 3y = 12
हल-
दी गई रैखिक समीकरण-युग्म है :
\(\frac{4}{3}\)x + 2y = 8
और 2x + 3y = 12
या \(\frac{4}{3}\)x + 2y - 8 = 0
और 2x + 3y - 12 = 0
यहाँ a₁ = \(\frac{4}{3}\), b₁ = 2, c₁ = -8
a₂ = 2, b₂ = 3, c₂ = -12

∴ समीकरण युग्म द्वारा निरूपित रेखाएं सम्पाती होंगी।
अतः, दी गई रैखिक समीकरण-युग्म संगत है। उत्तर

प्रश्न 4.
निम्न रैखिक समीकरणों के युग्मों में से कौनसे युग्म संगत/असंगत हैं, यदि संगत हैं तो ग्राफीय विधि से हल ज्ञात कीजिए :
(i) x + y = 5, 2x + 2y = 10
हल-
दी गई रैखिक समीकरण-युग्म है :
x + y = 5
और 2x + 2y = 10
या x + y - 5 = 0
2x + 2y - 10 = 0
उक्त समीकरण युग्म की तुलना समीकरण युग्म a₁x + b₁y + c₁ = 0 तथा a₂x + b₂y + c₂ = 0 से करने पर
यहाँ a₁ = 1, b₁ = 1, c₁ = -5
a₂ = 2, b₂ = 2, c₂ = -10

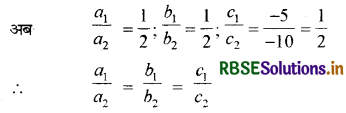
∴ समीकरण युग्म द्वारा निरूपित रेखाएँ सम्पाती होंगी।
अतः, दी गई रैखिक समीकरण-युग्म संगत है।
∴ दी गई रैखिक समीकरण युग्म का आलेख खींचने पर
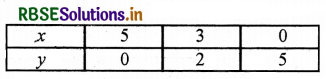
x + y = 5
x = 5 - y ......(1)
y = 0 को (1) में प्रतिस्थापित करने पर
x = 5 - 0 = 5
y = 3 को (1) में प्रतिस्थापित करने पर
x = 5 - 3 = 2
y = 5 को (1) में प्रतिस्थापित करने पर
x = 5 - 5 = 0

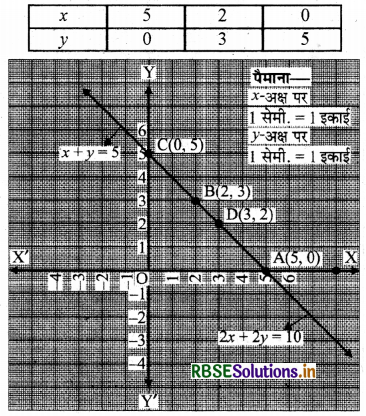
बिन्दुओं A(5, 0), B(2, 3), C(0, 5) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण x + y = 5 का आलेख प्राप्त होता है।
पुनः 2x + 2y = 10
या 2(x + y) = 10
या x + y = 5
या x = 5 - y ........(2)
y = 0 को (1) में प्रतिस्थापित करने पर
x = 5 - 0 = 5
y = 2 को (2) में प्रतिस्थापित करने पर
x = 5 - 2 = 3
y = 5 को (2) में प्रतिस्थापित करने पर
x = 5 - 5 = 0

बिन्दुओं A(5, 0), D(3, 2), C(0, 5) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण 2x + 2y = 10 का आलेख प्राप्त होता है।
आलेख से स्पष्ट है कि दी गई रैखिक समीकरण युग्म संपाती रेखाएँ हैं या इनके अपरिमित रूप से अनेक हल हैं।

(ii) x - y = 8, 3x - 3y = 16
हल-
दी गई रैखिक समीकरण-युग्म है :
x - y = 8
और 3x - 3y = 16
या x - y - 8 = 0
और 3x - 3y - 16 = 0
उक्त समीकरण युग्म की तुलना समीकरण युग्म a₁x + b₁y + c₁ = 0 तथा a₂x + b₂y + c₂ = 0 से करने पर
यहाँ a₁ = 1, b₁ = -1, c₁ = -8
a₂ = 3, b₂ = -3, c₂ = -16

दिये गये समीकरण युग्म का कोई हल नहीं होगा।
अतः, दी गई रैखिक समीकरण-युग्म असंगत है।

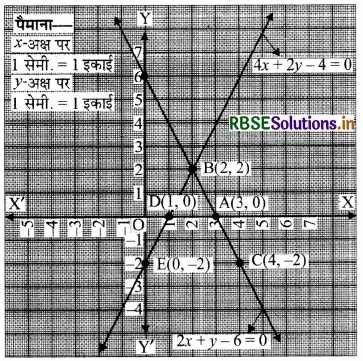
(iii) 2x + y - 6 = 0, 4x - 2y - 4 = 0
हल-
दी गई रैखिक समीकरण-युग्म है :
2x + y - 6 = 0
और 4x - 2y - 4 = 0
यहाँ a₁ = 2, b₁ = 1, c₁ = -6
a₂ = 4, b₂ = -2, c₂ = -4

दिये गये समीकरण युग्म का एक अद्वितीय हल होगा।
∴ दी गई रैखिक समीकरण-युग्म संगत है।
इन रैखिक समीकरणों का आलेख खींचने पर
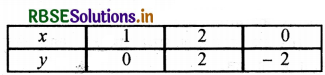
2x + y - 6 = 0
2x = 6 - y
या x = \(\frac{6-y}{2}\) .......(1)
y = 0 को (1) में प्रतिस्थापित करने पर,
x = \(\frac{6-0}{2}=\frac{6}{2}\) = 3
y = 2 को (1) में प्रतिस्थापित करने पर,
x = \(\frac{6-2}{2} = \frac{4}{2}\) = 2
y = -2 को (1) में प्रतिस्थापित करने पर,
x = \(\frac{6-(-2)}{2}=\frac{6+2}{2}\) = 4

बिन्दुओं A(3, 0), B(2, 2), C(4, -2) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण 2x + y - 6 = 0 का आलेख प्राप्त होता है।
पुनः 4x - 2y - 4 = 0
या 2[2x - y - 2] = 0
या 2x - y - 2 = 0
या 2x = y + 2
या x = \(\frac{y+2}{2}\) ........(2)
y = 0 को (2) में प्रतिस्थापित करने पर,
x = \(\frac{0+2}{2}=\frac{2}{2}\) = 1
y = 2 को (2) में प्रतिस्थापित करने पर,
x = \(\frac{2+2}{2}=\frac{4}{2}\) = 2
y = -2 को (2) में प्रतिस्थापित करने पर,
x = \(\frac{-2+2}{2}=\frac{0}{2}\) = 0

बिन्दुओं D(1, 0), B (2, 2), E(0, -2) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण 4x - 2y - 4 = 0 का आलेख प्राप्त होता है।
आलेख से यह स्पष्ट है कि दी गई समीकरण-युग्म बिन्दु B(2, 2) पर मिलती है।
अतः, दी गई रैखिक समीकरण-युग्म अद्वितीय है।

(iv) 2x - 2y - 2 = 0, 4x - 4y - 5 = 0
हल-
दी गई रैखिक किरण-युग्म है :
2x - 2y - 2 = 0
और 4x - 4y - 5 = 0
यहाँ a₁ = 2, b₁ = -2, c₁ = -2
a₂ = 4, b₂ = -4, c₂ = -5

∴ दिये गये समीकरण युग्म का कोई हल नहीं है।
अतः, दी गई समीकरण युग्म असंगत है।

प्रश्न 5.
एक आयताकार बाग, जिसकी लम्बाई, चौड़ाई से 4m अधिक है, का अर्ध परिमाप 36m है। बाग की विमाएँ ज्ञात कीजिए।
हल-
माना किबाग की लम्बाई = x m
बाग की चौड़ाई = y m
∴ बाग का परिमाप = 2[x + y] m
बाग के परिमाप का आधा = (x + y) m
प्रश्न की पहली शर्त के अनुसार,
x = y + 4
प्रश्न की दूसरी शर्त के अनुसार,
x + y = 36
∴ रैखिक समीकरण-युग्म है :
x = y + 4
और x + y = 36
x = y + 4 ......(1)
y = 0 को (1) में प्रतिस्थापित करने पर,
x = 0 + 4 = 4
y = -4 को (1) में प्रतिस्थापित करने पर,
x = -4 + 4 = 0
y = 16 को (1) में प्रतिस्थापित करने पर,
x = 16 + 4 = 20

बिन्दुओं A(4, 0), B(0, -4), C(20, 16) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण x = y + 4 का आलेख प्राप्त होता है।

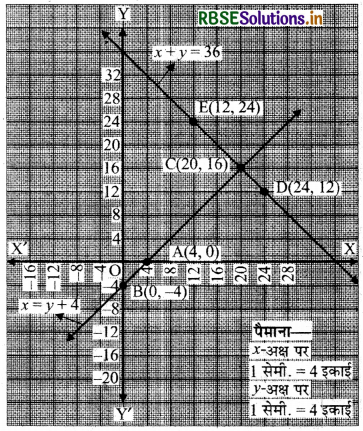
पुनः x + y = 36
x = 36 - y ......(2)
y = 12 को (2) में प्रतिस्थापित करने पर,
x = 36 - 12 = 24
y = 24 को (2) में प्रतिस्थापित करने पर,
x = 36 - 24 = 12
y = 16 को (2) में प्रतिस्थापित करने पर,
x = 36 - 16 = 20

बिन्दुओं D(24, 12), E(12, 24), C(20, 16) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण x + y = 36 का आलेख प्राप्त होता है।
आलेख से यह स्पष्ट है कि रैखिक समीकरणों का युग्म बिन्दु C(20, 16) पर मिलता है।
∴ C(20, 16) अर्थात् x = 20 और y = 10 रैखिक समीकरण युग्म का हल है।
अतः, बाग की लम्बाई = 20m
बाग की चौड़ाई = 16 m

प्रश्न 6.
एक रैखिक समीकरण 2x + 3y - 8 = 0 दी गई है। दो चरों में एक ऐसी और रैखिक समीकरण लिखिए ताकि प्राप्त युग्म का ज्यामितीय निरूपण जैसा कि
(i) प्रतिच्छेद करती रेखाएँ हों
(ii) समान्तर रेखाएँ हों
(iii) संपाती रेखाएँ हों।
हल-
दिया गया रैखिक समीकरण 2x + 3y - 8 = 0
इस समीकरण की व्यापक रैखिक समीकरण a₁x + b₁y + c₁ = 0 से तुलना करने पर,
a₁ = 2, b₁ = 3, c₁ = -8
(i) जब समीकरण युग्म, प्रतिच्छेद करती हुई रेखाएँ निरूपित करता है तो शर्त
\(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
⇒ \(\frac{2}{a_{2}} \neq \frac{3}{b_{2}}\)
अर्थात् a₂ का मान 2 अथवा 0 नहीं होना चाहिए और b₂ का मान 3 अथवा 0 नहीं होना चाहिए।
जहाँ a₂ ≠ 2 अथवा b₂ ≠ 3 और a₂ ≠ 0, b₂ ≠ 0 है।
अतः सम्भावित रैखिक समीकरण 3x + 2y - 7 = 0 प्रकार की होगी।

(ii) जब समीकरण युग्म समान्तर रेखाएँ निरूपित करता है तो शर्त-
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
\(\frac{2}{a_{2}}=\frac{3}{b_{2}} \neq \frac{-8}{c_{2}}\)
\(\frac{2}{a_{2}}=\frac{3}{b_{2}}\)
⇒ \(\frac{a_{2}}{b_{2}}=\frac{2}{3}\)
अर्थात् a₂ और b₂ का मान 2 : 3 में होना चाहिए।
माना a₂ = 2k तथा b₂ = 3k, जहाँ k एक स्थिरांक है।
\(\frac{3}{b_{2}} \neq \frac{-8}{c_{2}}\)
\(\frac{3}{3 k} \neq \frac{-8}{c_{2}}\)
⇒ c₂ ≠ -8k
अतः अभीष्ट रैखिक समीकरण
2kx + 3ky - mk = 0, m ≠ -8
अतः सम्भावित रैखिक समीकरण 2x + 3y - 12 = 0 प्रकार की होगी।

(iii) जब समीकरण युग्म सम्पाती रेखाएँ निरूपित करता है तो शर्त-
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
⇒ \(\frac{2}{a_{2}}=\frac{3}{b_{2}}=\frac{-8}{c_{2}}=\frac{1}{k}\)
⇒ a₂ = 2k, b₂ = 3k और c₂ = -8k
अतः अभीष्ट समीकरण 2kx + 3ky - 8k = 0, जहाँ k एक आनुपातिक स्थिरांक है।
अतः सम्भावित रैखिक समीकरण 4x + 6y - 16 = 0 प्रकार की होगी।

प्रश्न 7.
समीकरणों x - y + 1 = 0 और 3x + 2y - 12 = 0 का ग्राफ खींचिए। x-अक्ष और इन रेखाओं से बने त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए और त्रिभुजाकार पटल को छायांकित कीजिए।
हल-
रैखिक समीकरण-युग्म लेने पर
x - y + 1 = 0
और 3x + 2y - 12 = 0
या x - y + 1 = 0
या x = y - 1 ......(1)
y = 0 को (1) में प्रतिस्थापित करने पर,
x = 0 - 1 = -1
y = 3 को (1) में प्रतिस्थापित करने पर,
x = 3 - 1 = 2
y = 1 को (1) में प्रतिस्थापित करने पर,
x = 1 - 1 = 0

बिन्दुओं A(-1, 0), B(2, 3), C(0, 1) को आलेखित करने और उनको मिलाकर रेखा खींचने पर हमें समीकरण x - y + 1 = 0 का आलेख प्राप्त होता है।

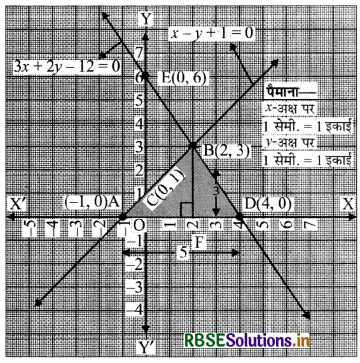
3x + 2y - 12 = 0
या 3x = 12 - 2y
या x = \(\frac{12-2 y}{3}\) .......(2)
y = 0 को (2) में प्रतिस्थापित करने पर,
x = \(\frac{12-2 \times 0}{3}=\frac{12}{3}\) = 4
y = 3 को (2) में प्रतिस्थापित करने पर,
x = \(\frac{12-2 \times 3}{3}=\frac{12-6}{3}\) = 2
y = 6 को (2) में प्रतिस्थापित करने पर,
x = \(\frac{12-2 \times 6}{3} = \frac{12-12}{3}\) = 0

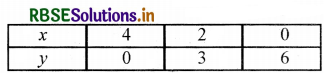
बिन्दुओं D(4, 0), B(2, 3), E(0, 6) को आलेखित करने और उनको मिलाकर रेखा खींचने पर हमें समीकरण 3x + 2y - 12 = 0 आलेख प्राप्त होता है।
रैखिक समीकरणों के युग्म और x-अक्ष द्वारा बनाए गए त्रिभुज के शीर्षों को आलेख में छायांकित किया गया है।
∆ABD इस प्रकार बना त्रिभुज है।
∆ABD के शीर्षों के निर्देशांक हैं : A(-1, 0), B(2, 3) और D(4,0)