RBSE Solutions for Class 10 Maths Chapter 15 Probability Ex 15.2

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 15 Probability Ex 15.2 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 15 Probability Ex 15.2

Question 1.
The customers Shyam and Ekta are visiting a particular shop in the same week (Tuesday to Saturday). Each is equally likely to visit the shop on any day as on another day. What is the probability that both will visit the shop on (i) the same day? (ii) consecutive days? (iii) different days?
Solution:
When Shyam and Ekta are visiting a particular ship in the same weak, then the possible outcomes are:
S = {(T, T), (T, W), (T, Th), (T, F), (T, S), (W, T), (W, W), (W, Th), (W, F), (W, S), (Th, T), (Th, W), (Th, Th), (Th, F), (Th, S), (F, T), (F, W), (F, Th), (F, F), (F, S), (S, T), (S, W), (S, Th), (S, F), (S, S)}
Here T is for Tuesday
W is for Wednesday
Th is for Thursday
F is for Friday
and S is for Saturday
n(S) = 25
Let A be the event that ‘Shyam and Ekta are visiting a particular shop on the same day.’
A = {(T, T), (W, W), (Th, Th), (F, F), (S, S)}
n(A) = 5
(i) Probability that both will visit a particular shop on the same day = \(\frac{5}{25}\)
∴ P(A) = \(\frac{5}{25}\)

(ii) Let B be the event that ‘both visit a particular shop on consecutive day.'
∴ B = {(T, W), (W, T), (W, Th), (Th, W), (Th, F), (F, Th), (F, S), (S, F)}
n(B) = 8
∴ Probability' that both will visit a particular shop on consecutive days = \(\frac{8}{25}\)

(iii) Probability that both will visit a particular shop on different days = 1 - Probability that both will visit a particular shop on the same day
= 1 - \(\frac{1}{5}\) [∵ \(P(\overline{\mathrm{A}})\) = 1 - P(A)]
= \(\frac{4}{5}\)
or \(P(\overline{\mathrm{A}}) = \frac{4}{5}\)

Question 2.
A die is numbered in such a way that its faces show the numbers 1, 2, 2, 3, 3, 6. It is thrown two times and the total score in two throws is noted. Complete the following table which gives a few values of the total score on the two throws:

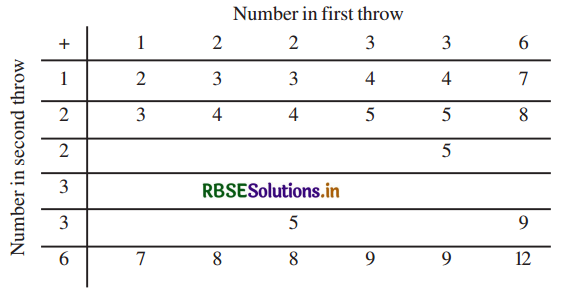
What is the probability that the total score is (i) even? (ii) 6? (iii) at least 6?
Solution:
The completed Table is:

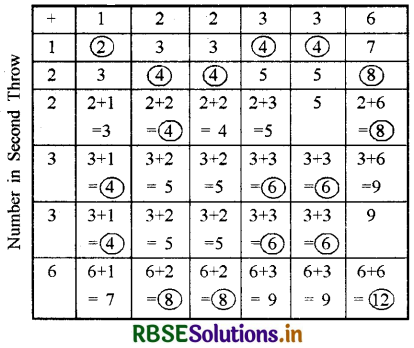
Number of possibe outcomes is 6 × 6 = 36
(i) Let A be the event of getting ‘the total score an even number’
A = {2, 4, 4, 4, 4, 4, 4, 4, 4, 6, 6, 6, 6, 8, 8, 8, 8, 12}
n(A) = 18
∴ Probability of getting the total score an even number = \(\frac{18}{36}=\frac{1}{2}\)
⇒ P(even number) = \(\frac{1}{2}\)
(ii) Let B be the event of getting ‘the total score 6’.
B = {6, 6, 6, 6}
n(B) = 4
∴ Probability of getting the total score 6 = \(\frac{4}{36}\)
P(B) = \(\frac{1}{9}\)
(iii) Let C be the event of getting ‘the total score at least 6’.
C = {6, 6, 6, 6, 7, 7, 8, 8, 8, 8, 9, 9, 9, 9, 12}
n(C) = 15
∴ Probability of getting ‘the total score atleast 6’ = \(\frac{15}{36}=\frac{5}{12}\)
∴ P(C) = \(\frac{5}{12}\)

Question 3.
A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball is double that of a red ball, determine the number of blue balls in the bag.
Solution:
Number of red balls = 5
Let the number of blue balls = x
∴ Total number of balls = 5 + x
Probability of drawing a blue ball = \(\frac{x}{5+x}\)
Similarly, probability of drawing a red ball = \(\frac{5}{5+x}\)
Since it is given in the question that the probability of drawing a blue ball is double that of drawing a red ball.
∴ Probability of drawing a blue ball = 2(Probability of drawing a red ball)
⇒ \(\frac{x}{5+x}=2\left(\frac{5}{5+x}\right)\)
⇒ \(\frac{x}{5+x}=\frac{10}{5+x}\)
∴ x = 10
Therefore the number of blue balls in the bag = 10

Question 4.
A box contains 12 balls out of which x are black. If one ball is drawn at random from the box, what is the probability that it will be a black ball?
If 6 more black balls are put in the box, the probability of drawing a black ball is now double what it was before. Find it.
Solution:
Total number of balls in the box = 12
Number of black balls = x
∴ Probability of drawing a black ball = \(\frac{x}{12}\)
If 6 more black balls are put in the box, then the total number of balls in the box = 12 + 6 = 18
Number of black balls = x + 6
∴ Probability of drawing a black ball = \(\frac{x+6}{18}\)
According to the questions,
Probability of drawing a black ball now = 2 × (Probability of drawing a black ball in former case)
⇒ \(\frac{x+6}{18}=2 \times \frac{x}{12}\)
⇒ \(\frac{x+6}{3}=\frac{2 x}{2}\)
⇒ \(\frac{x+6}{3}\) = x
⇒ x + 6 = 3x
⇒ x = 3
∴ Number of black balls = 3

Question 5.
A jar contains 24 marbles, some are green and others are blue. If a marble is drawn at random from the jar, the probability that it is green is \(\frac{2}{3}\). Find the number of blue balls in the jar.
Solution:
Total number of marbles in the jar = 24
Let the number of green marbles = x
∴ Number of blue marbles = 24 - x
When one marble is drawn, then probability that it is green = \(\frac{2}{3}\)
∴ \(\frac{x}{24}=\frac{2}{3}\)
⇒ x = \(\frac{24 \times 2}{3}\)
⇒ x = 16
∴ Number of green marbles = 16
∴ Number of blue marbles = 24 - x
= 24 - 16
= 8