RBSE Solutions for Class 10 Maths Chapter 15 प्रायिकता Ex 15.1

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 15 प्रायिकता Ex 15.1 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 15 प्रायिकता Ex 15.1

प्रश्न 1.
निम्नलिखित कथनों को पूरा कीजिए :
(i) घटना E की प्रायिकता + घटना 'E नहीं' की प्रायिकता = __________ है।
(ii) उस घटना की प्रायिकता जो घटित नहीं हो सकती __________ है। ऐसी घटना __________ कहलाती है।
(iii) उस घटना की प्रायिकता जिसका घटित होना निश्चित है __________ है। ऐसी घटना __________ कहलाती है।
(iv) किसी प्रयोग की सभी प्रारम्भिक घटनाओं की प्रायिकताओं का योग __________ है।
(v) किसी घटना की प्रायिकता __________ से बड़ी या उसके बराबर होती है तथा __________ से छोटी या उसके बराबर होती है।
हल-
(i) 1
(ii) 0, असम्भव घटना
(iii) 1, अवश्य, या निश्चित घटना 
(iv) 1
(v) 0, 1

प्रश्न 2.
निम्नलिखित प्रयोगों में से किन-किन प्रयोगों के परिणाम समप्रायिक हैं? स्पष्ट कीजिए :
(i) एक ड्राइवर कार चलाने का प्रयत्न करता है। कार चलनी प्रारम्भ हो जाती है या कार चलना प्रारम्भ नहीं होती है।
(ii) एक खिलाड़ी बास्केटबॉल को बॉस्केट में डालने का प्रयत्न करती है। वह बास्केट में बॉल डाल पाती है या नहीं डाल पाती है।
(iii) एक सत्य-असत्य प्रश्न का अनुमान लगाया जाता है। उत्तर सही है या गलत होगा।
(iv) एक बच्चे का जन्म होता है। वह एक लड़का है या एक लड़की है।
उत्तर-
(i) जब एक ड्राइवर कार चलाने का प्रयत्न करता है तो सामान्य स्थिति में कार चलने लगती है परन्तु यदि कार में कोई दोष हो, तो कार नहीं चलती इसलिए परिणाम समप्रायिक नहीं है।

(ii) जब एक खिलाड़ी बास्केट बॉल को बास्केट में डालने का प्रयत्न करती है, तो इस स्थिति में परिणाम समप्रायिक नहीं है क्योंकि परिणाम कई तथ्यों पर निर्भर करता है। जैसे खिलाड़ी का प्रशिक्षण, प्रयोग की जाने वाली बन्दूक की प्रकृति आदि।

(iii) एक प्रश्न के लिए दो सम्भावनाएँ या तो सही या गलत हैं। सत्य- असत्य के इस प्रश्न के इस अभिप्रयोग में एक ही परिणाम हो सकता है : सत्य या असत्य अर्थात् इस घटना के होने का एक ही अवसर है इसलिए दो परिणाम समप्रायिक हैं।

(iv) एक नव जन्मा बच्चा (जिसका जन्म इसी क्षण हुआ है) एक लड़का भी हो सकता है और एक लड़की भी हो सकती है और दोनों पर परिणाम समप्रायिक हैं।

प्रश्न 3.
फुटबॉल के खेल को प्रारम्भ करते समय यह निर्णय लेने के लिए कि कौनसी टीम पहले बॉल लेगी, इसके लिए सिक्का उछालना एक न्यायसंगत विधि क्यों माना जाता है?
उत्तर-
जब सिक्के को उछाला जाता है तो केवल दो ही सम्भावनाएँ होती हैं अर्थात् परिणाम चित या पट दो समप्रायिक हैं। एक सिक्का उछालने के परिणाम की पूर्व भविष्यवाणी नहीं की जा सकती।

प्रश्न 4.
निम्नलिखित में से कौनसी संख्या किसी घटना की प्रायिकता नहीं हो सकती?
(A) \(\frac{2}{3}\)
(B) -1.5
(C) 15%
(D) 0.7
हल-
हम जानते हैं कि एक घटना की प्रायिकता 0 से कम और 1 से अधिक नहीं हो सकती अर्थात् 0 ≤ P(E) ≤ 1
∴ (B) -1.5 सम्भव नहीं है।

प्रश्न 5.
यदि P(E) = 0.05 है, तो 'E नहीं' की प्रायिकता क्या है?
हल-
हम जानते हैं कि P(E) + P(\(\overline{\mathrm{E}}\)) = 1
P(\(\overline{\mathrm{E}}\)) = 1 - P(E)
= 1 - 0.05
= 0.95

प्रश्न 6.
एक थैले में केवल नींब की महक वाली मीठी गोलियाँ हैं। मालिनी बिना थैले में झाँके उसमें से एक गोली निकालती है। इसकी क्या प्रायिकता है कि वह निकाली गई गोली
(i) संतरे की महक वाली है?
(ii) नींबू की महक वाली है?
हल-
(i) क्योंकि एक थैले में केवल नींबू की महक वाली मीठी गोलियाँ हैं।
अतः यहाँ संतरे की महक वाली कोई गोली नहीं है।
अतः, यह एक असम्भव घटना है।
∴ संतरे की महक वाली गोली की प्रायिकता = 0

(ii) क्योंकि थैले में केवल नींबू की महक वाली ही गोलियाँ हैं। इसलिए यह एक निश्चित घटना है।
∴ नींबू की महक वाली गोलियाँ निकालने की प्रायिकता = \(\frac{1}{1}\) = 1

प्रश्न 7.
यह दिया हुआ है कि 3 विद्यार्थियों के एक समूह में से 2 विद्यार्थियों के जन्मदिन एक ही दिन न होने की प्रायिकता 0.992 है। इसकी क्या प्रायिकता है कि इन 2 विद्यार्थियों का जन्मदिन एक ही दिन हो?
हल-
दो विद्यार्थियों के एक ही दिन होने की घटना को E मान लीजिए।
∴ दो विद्यार्थियों के जन्म एक ही दिन न होने की घटना (\(\overline{\mathrm{E}}\)) है।
∴ P(\(\overline{\mathrm{E}}\)) = 0.992
∴ P(E) = 1 - P(\(\overline{\mathrm{E}}\)) [∵ (P(E) + P(\(\overline{\mathrm{E}}\)) = 1)]
= 1 - 0.992
= 0.008
∴ दो विद्यार्थियों का जन्म एक ही दिन होने की प्रायिकता 0.008 है।

प्रश्न 8.
एक थैले में 3 लाल और 5 काली गेंदें हैं। इस थैले में से एक गेंद यादृच्छया निकाली जाती है। इसकी प्रायिकता क्या है कि गेंद
(i) लाल हो?
(ii) लाल नहीं हो?
हल-
लाल गेंदों की संख्या = 3
काली गेंदों की संख्या = 5
गेंदों की कुल संख्या = 3 + 5 = 8
एक गेंद यादृच्छया निकाली गई है
(i) लाल गेंद प्राप्त करने की प्रायिकता

P(लाल गेंद) = \(\frac{3}{8}\)

(ii) लाल गेंद न प्राप्त करने की प्रायिकता = 1 - P(लाल गेंद)
= 1 - \(\frac{3}{8}\)
= \(\frac{5}{8}\) [∵ P(\(\overline{\mathrm{E}}\)) = 1 - P(E)]

प्रश्न 9.
एक डिब्बे में 5 लाल कंचे, 8 सफेद कंचे और 4 हरे कंचे हैं। इस डिब्बे में से एक कंचा यादृच्छया निकाला जाता है। इसकी क्या प्रायिकता है कि निकाला गया कंचा
(i) लाल है?
(ii) सफेद है?
(iii) हरा नहीं है?
हल-
लाल कंचों की संख्या = 5
सफेद कंचों की संख्या = 8
हरे कंचों की संख्या = 4
कंचों की कुल संख्या = 5 + 8 + 4 = 17
क्योंकि एक कंचा निकाला गया है।
(i) लाल कंचे 5 हैं।
लाल कंचा निकालने की प्रायिकता

(ii) क्योंकि सफेद कंचे 8 हैं।
सफेद कंचा निकालने की प्रायिकता

(iii) हरे कंचे 4 हैं।
हरा कंचा निकालने की प्रायिकता

∴ हरा कंचा न निकालने की प्रायिकता = 1 - हरा कंचा निकालने की प्रायिकता
= 1 - \(\frac{4}{17}\)
= \(\frac{13}{17}\)

प्रश्न 10.
एक पिग्गी बैंक (piggy bank) में, 50 पैसे के सौ सिक्के हैं, 1 रु. के पचास सिक्के हैं, 2 रु. के बीस सिक्के और 5 रु. के दस सिक्के हैं। यदि पिग्गी बैंक को हिलाकर उल्टा करने पर कोई एक सिक्का गिरने के परिणाम समप्रायिक हैं, तो इसकी क्या प्रायिकता है कि वह गिरा हुआ सिक्का
(i) 50 पैसे का होगा?
(ii) 5 रु. का नहीं होगा?
हल-
50 पैसे के सिक्कों की संख्या = 100
1 रु. के सिक्कों की संख्या = 50
2 रु. के सिक्कों की संख्या = 20
5 रु. के सिक्कों की संख्या = 10
∴ सिक्कों की कुल संख्या = 100 + 50 + 20 + 10 = 180
(i) चूँकि 50 पैसे के 100 सिक्के हैं,
50 पैसे के सिक्के प्राप्त करने की प्रायिकता

P(50P के सिक्के) = \(\frac{5}{9}\)

(ii) 5 रु. के सिक्कों की संख्या = 10
∴ 5 रु. के सिक्के प्राप्त करने की प्रायिकता

P(5 रु. के सिक्के) = \(\frac{10}{180}=\frac{1}{18}\)
5 रु. के सिक्के प्राप्त न करने की प्रायिकता = 1 - P(5 रु. के सिक्के)
=1 - \(\frac{1}{18}\)
= \(\frac{17}{18}\)

प्रश्न 11.
गोपी अपने जल-जीव कुण्ड (aquarium) के लिए एक दुकान से मछली खरीदती है। दुकानदार एक टंकी, जिसमें 5 नर मछली और 8 मादा मछली हैं, में से एक मछली यादृच्छया उसे देने के लिए निकालती है (देखिए आकृति)। इसकी क्या प्रायिकता है कि निकाली गई मछली नर मछली है?

हल-
नर मछलियों की संख्या = 5
मादा मछलियों की संख्या = 8
जल जीव कुण्ड में मछलियों की कुल संख्या = 5 + 8 = 13
नर मछली प्राप्त करने की प्रायिकता

P(नर मछली) = \(\frac{5}{13}\)

प्रश्न 12.
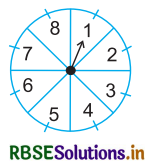
संयोग (chance) के एक खेल में, एक तीर को घुमाया जाता है, जो विश्राम में आने के बाद संख्याओं 1, 2, 3, 4, 5, 6, 7 और 8 में से किसी एक संख्या को इंगित करता है (देखिए आकृति)। यदि ये सभी परिणाम समप्रायिक हों तो इसकी क्या प्रायिकता है कि यह तीर इंगित
(i) 8 को करेगा?
(ii) एक विषम संख्या को करेगा?
(iii) 2 से बड़ी संख्या को करेगा?
(iv) 9 से छोटी संख्या को करेगा?

हल-
(i) परिणामों की कुल संख्या = {1, 2, 3, 4, 5, 6, 7, 8}
तीर द्वारा संख्या 8 को इंगित करने की प्रायिकता

'8' प्राप्त करने की प्रायिकता = \(\frac{1}{8}\)

(ii) विषम संख्याएँ हैं = {1, 3, 5, 7}
तीर द्वारा एक विषम संख्या इंगित करने के परिणामों की संख्या = 4
∴ विषम संख्या इंगित होने की प्रायिकता

विषम संख्या प्राप्त करने की प्रायिकता = \(\frac{4}{8}=\frac{1}{2}\)

(iii) 2 से बड़ी संख्याएँ हैं = {3, 4, 5, 6, 7, 8}
2 से बड़ी संख्या को इंगित करने की घटना के अनुकूल परिणामों की संख्या = 6
∴ 2 से बड़ी संख्या को इंगित करने की प्रायिकता

∴ 2 से बड़ी संख्याएँ प्राप्त करने की प्रायिकता 2 = \(\frac{6}{8}=\frac{3}{4}\)
P(2 से बड़ी संख्या) = \(\frac{3}{4}\)

(iv) 9 से छोटी संख्याएँ हैं = {1, 2, 3, 4, 5, 6, 7, 8}
9 से छोटी संख्या इंगित करने की घटना के अनुकूल परिणामों की संख्या = 8
अतः 9 से छोटी संख्या इंगित करने की प्रायिकता

∴ 9 से छोटी संख्या प्राप्त करने की प्रायिकता = \(\frac{8}{8}\) = 1
P(9 से छोटी संख्या) = 1

प्रश्न 13.
एक पासे को एक बार फेंका जाता है। निम्नलिखित को प्राप्त करने की प्रायिकता ज्ञात कीजिए :
(i) एक अभाज्य संख्या
(ii) 2 और 6 के बीच स्थित कोई संख्या
(iii) एक विषम संख्या।
हल-
जब पासे को एक बार फेंका जाता है तो सम्भव परिणाम हैं
S = {1, 2, 3, 4, 5, 6}
(i) अभाज्य संख्याएँ हैं : {2, 3, 5}
∴ अभाज्य संख्या प्राप्त करने की प्रायिकता = \(\frac{3}{6}=\frac{1}{2}\)

(ii) 2 और 6 के बीच स्थित संख्याएँ = {3, 4, 5}
2 और 6 के बीच स्थित संख्या प्राप्त करने की प्रायिकता = \(\frac{3}{6}=\frac{1}{2}\)

(iii) विषम संख्याएँ हैं = {1, 3, 5}
एक विषम संख्या प्राप्त करने की प्रायिकता = \(\frac{3}{6}=\frac{1}{2}\)
P(एक विषम संख्या) = \(\frac{1}{2}\)

प्रश्न 14.
52 पत्तों की अच्छी प्रकार से फेंटी गई एक गड्डी में से एक पत्ता निकाला जाता है। निम्नलिखित को प्राप्त करने की प्रायिकता ज्ञात कीजिए :
(i) लाल रंग का बादशाह
(ii) एक फेस कार्ड अर्थात् तस्वीर वाला पत्ता
(ii) लाल रंग की तस्वीर वाला पत्ता।
(iv) पान का गुलाम
(v) हुकुम का पत्ता
(vi) एक ईंट की बेगम।
हल-
52 पत्तों की एक गड्डी में पत्तों की संख्या 52 है।
(i) लाल रंग के दो बादशाह हैं अर्थात् पान का बादशाह और ईंट का बादशाह
लाल रंग का बादशाह प्राप्त करने की प्रायिकता = \(\frac{2}{52}=\frac{1}{26}\)
P(लाल रंग का बादशाह) = \(\frac{1}{26}\)

(ii) 12 फेस कार्ड हैं अर्थात् 4 गुलाम, 4 बेगम और 4 बादशाह
तस्वीर वाला पत्ता प्राप्त करने की प्रायिकता = \(\frac{12}{52}\)
∴ P (एक फेस कार्ड) =\(\frac{3}{13}\)

(iii) क्योंकि लाल रंग के 6 पत्ते हैं अर्थात् 2 गुलाम, 2 बेगम और 2 बादशाह हैं।
∴ 6 लाल रंग के फेस कार्ड प्राप्त करने की प्रायिकता = \(\frac{6}{52}\)
P(लाल रंग का फेस कार्ड) = \(\frac{3}{26}\)

(iv) पान का केवल एक ही गुलाम है।
∴ एक पान का गुलाम प्राप्त करने की प्रायिकता = \(\frac{1}{52}\)
P(एक पान का गुलाम) = \(\frac{1}{52}\)

(v) चूँकि हुकुम के 13 पत्ते हैं
∴ हुकुम का पत्ता प्राप्त करने की प्रायिकता = \(\frac{13}{52}\)
P(एक हुकुम का पत्ता) = \(\frac{1}{4}\)

(vi) चूँकि ईंट की बेगम केवल एक ही है
∴ ईंट की बेगम प्राप्त करने की प्रायिकता = \(\frac{1}{52}\)
P(ईंट की प्रायिकता) = \(\frac{1}{52}\)

प्रश्न 15.
ताश के पाँच पत्तों-ईंट का दहला, गुलाम, बेगम, बादशाह और इक्का, को पलट कर के अच्छी प्रकार फेंटा जाता है। फिर इनमें से यादृच्छया एक पत्ता निकाला जाता है :
(i) इसकी क्या प्रायिकता है कि यह पत्ता एक बेगम है?
(ii) यदि बेगम निकल आती है, तो उसे अलग रख दिया जाता है और एक अन्य पत्ता निकाला जाता है। इसकी क्या प्रायिकता है कि दूसरा निकाला गया पत्ता
(a) एक इक्का है?
(b) एक बेगम है?
हल-
पाँच पत्ते ईंट का दहला, गुलाम, बेगम, बादशाह और इक्का हैं।
(i) बेगम प्राप्त करने की प्रायिकता = \(\frac{1}{5}\)
∴ P(एक बेगम) = \(\frac{1}{5}\)

(ii) यदि बेगम निकल आती है, तो उसे अलग रख दिया जाता है तो चार पत्ते बच जाते हैं : ईंट का दहला, गुलाम, बादशाह और इक्का
(a) इक्का प्राप्त करने की प्रायिकता = \(​​\)\(\frac{1}{4}\)
P(एक इक्का) =\(\frac{1}{4}\)
कोई बेगम नहीं बची।
(b) बेगम प्राप्त करने की प्रायिकता = \(\frac{0}{4}\) = 0
P(एक बेगम) = 0

प्रश्न 16.
किसी कारण 12 खराब पेन 132 अच्छे पेनों में मिल गए हैं। केवल देखकर यह नहीं बताया जा सकता है कि कोई पेन खराब है या अच्छा है। इस मिश्रण में से, एक पेन यादृच्छया निकाला जाता है। निकाले गए पेन की अच्छा होने की प्रायिकता ज्ञात कीजिए।
हल-
खराब पेनों की संख्या = 12
अच्छे पेनों की संख्या = 132
पेनों की कुल संख्या = 12 + 132 = 144
अच्छा पेन प्राप्त करने की प्रायिकता = \(\frac{132}{144}=\frac{11}{12}\)
P(एक अच्छा पेन) = \(\frac{11}{12}\)

प्रश्न 17.
(i) 20 बल्बों के एक समूह में 4 बल्ब खराब हैं। इस समूह में से एक बल्ब यादृच्छया निकाला जाता है। इसकी क्या प्रायिकता है कि यह बल्ब खराब होगा?
(ii) मान लीजिए (i) में निकाला गया बल्ब खराब नहीं है और न ही इसे दुबारा बल्बों के साथ मिलाया जाता है। अब शेष बल्बों में से एक बल्ब यादृच्छया निकाला जाता है। इसकी क्या प्रायिकता है कि यह बल्ब खराब नहीं होगा?
हल-
(i) खराब बल्बों की संख्या = 4
अच्छे बल्बों (खराब नहीं) की संख्या = 16
बल्बों की कुल संख्या = 4 + 16 = 20
खराब बल्ब प्राप्त करने की प्रायिकता = \(\frac{4}{20}=\frac{1}{5}\)

(ii) जब निकाला गया बल्ब दोबारा बल्बों के साथ नहीं मिलाया जाता है, तो 19 बल्ब शेष बच जाते हैं।
अब खराब बल्ब प्राप्त करने की प्रायिकता = \(\frac{4}{19}\)
अब खराब बल्ब प्राप्त न होने की प्रायिकता = 1 - \(\frac{4}{19} = \frac{15}{19}\)
∴ P(खराब बल्ब नहीं) = \(\frac{15}{19}\)

प्रश्न 18.
एक पेटी में 90 डिस्क (discs) हैं, जिन पर 1 से 90 तक संख्याएँ अंकित हैं। यदि इस पेटी में से एक डिस्क यादृच्छया निकाली जाती है तो इसकी प्रायिकता ज्ञात कीजिए कि इस डिस्क पर अंकित होगी:
(i) दो अंकों की एक संख्या
(ii) एक पूर्ण वर्ग संख्या
(iii) 5 से विभाज्य एक संख्या।
हल-
1 से 90 तक कुल 90 संख्याएँ हैं और 10 से 90 तक 81 संख्याएँ दो अंकों वाली हैं।
(i) दो अंकों वाली संख्या प्राप्त करने की प्रायिकता = \(\frac{81}{90}\)
∴ P(दो अंकों की एक संख्या) = \(\frac{81}{90} = \frac{9}{10}\)

(ii) पूर्ण वर्ग संख्याएँ हैं : {1, 4, 9, 16, 25, 36, 49, 64, 81}
1 से 90 तक 9 पूर्ण वर्ग संख्याएँ हैं।
पूर्ण वर्ग संख्या प्राप्त करने की प्रायिकता = \(\frac{9}{90}=\frac{1}{10}\)
P(एक पूर्ण वर्ग संख्या) = \(\frac{1}{10}\)

(iii) 5 से विभाज्य संख्याएँ हैं : = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90}
5 से विभाज्य 18 संख्याएँ हैं :
∴ 5 से विभाज्य संख्या प्राप्त करने की प्रायिकता = \(\frac{18}{90} = \frac{1}{5}\)
∴ अभीष्ट प्रायिकता =\( \frac{1}{5}\)

प्रश्न 19.
एक बच्चे के पास ऐसा पासा है जिसके फलकों पर निम्नलिखित अक्षर अंकित हैं :

इस पासे को एक बार फेंका जाता है। इसकी क्या प्रायिकता है कि
(i) A प्राप्त हो?
(ii) D प्राप्त हो?
हल-
पासे के फलकों की संख्या = 6
S = {A, B, C, D, E, A}
n(S) = 6
(i) चूँकि दो फलकों पर A हैं।
∴ A प्राप्त करने की प्रायिकता = \(\frac{2}{6}=\frac{1}{3}\)
P(A) = \(\frac{1}{3}\)

(ii) चूँकि केवल एक फलक पर D अंकित है।
D प्राप्त करने की प्रायिकता = \(\frac{1}{6}\)
∴ P(D) = \(\frac{1}{6}\)

प्रश्न 20.
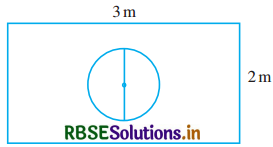
मान लीजिए आप एक पासे को आकृति में दर्शाए आयताकार क्षेत्र में यादृच्छया रूप से गिराते हैं। इसकी क्या प्रायिकता है कि वह पासा 1 m व्यास वाले वृत्त के अन्दर गिरेगा?

हल-
आयत की लम्बाई (l) = 3 m
आयत की चौड़ाई (b) = 2 m
∴ आयत का क्षेत्रफल = 3 m × 2 m = 6 m²
वृत्त का व्यास = 1 m
वृत्त की त्रिज्या (R) = \(\frac{1}{2}\) m
∴ वृत्त का क्षेत्रफल = πR²
= \(\pi\left(\frac{1}{2}\right)^{2}\)
= \(\frac{\pi}{4}\) m²

∴ अभीष्ट प्रायिकता = \(\frac{\pi}{24}\)

प्रश्न 21.
144 बॉल पेनों के एक समूह में 20 बॉल पेन खराब हैं और शेष अच्छे हैं। आप वही पेन खरीदना चाहेंगे जो अच्छा हो, परन्तु ख़राब पेन आप खरीदना नहीं चाहेंगे। दुकानदार इन पेनों में से, यादृच्छया एक पेन निकालकर आपको देता है। इसकी क्या प्रायिकता है कि
(i) आप वह पेन खरीदेंगे?
(ii) आप वह पेन नहीं खरीदेंगे?
हल-
समूह में बॉल पेनों की कुल संख्या = 144
खराब पेनों की संख्या = 20
∴ अच्छे पेनों की संख्या = 144 - 20 = 124
(i) माना कि आप वह पेन खरीदने की घटना A है
∴ पेन खरीदने की प्रायिकता = \(\frac{124}{144}\)
P(A) = \(\frac{31}{36}\)

(ii) वह पेन नहीं खरीदने की घटना \(\overline{\mathrm{A}}\) होगी :
P(\(\overline{\mathrm{A}}\)) = 1 - P(A)
= 1 - \(\frac{31}{36}\)
= \(\frac{5}{36}\)
∴ P(पेन नहीं खरीदने) = \(\frac{5}{36}\)

प्रश्न 22.
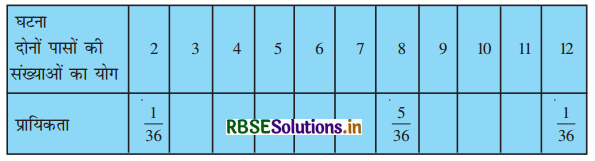
एक सलेटी पासे और एक नीले पासे को एक साथ फेंका जाता है। सभी सम्भावित परिणामों को लिखिए।
(i) निम्नलिखित सारणी को पूरा कीजिए :

(ii) एक विद्यार्थी यह तर्क देता है कि 'यहाँ कुल 11 परिणाम 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 और 12 हैं। अतः, प्रत्येक की प्रायिकता \(\frac{1}{11}\) है।' क्या आप इस तर्क से सहमत हैं? सकारण उत्तर दीजिए।
हल-
(i) जब दो पासे फेंके जाते हैं तो सम्भाव्य परिणामों की कुल संख्या है :
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n(S) = 36
माना कि 'योग 3 प्राप्त करना' घटना A है।
∴ A = {(1, 2), (2, 1)}
n(A) = 2
∴ योग 3 प्राप्त करने की प्रायिकता = \(\frac{2}{36}\)
P(A) = \(\frac{2}{36}\)
माना कि 'योग 4 प्राप्त करना' घटना B है
B = {(1, 3), (3, 1), (2, 2)}
n(B) = 3
∴ P(B) = \(\frac{3}{36}\)
माना कि 'योग 5 प्राप्त करना' घटना C है
C = {(1, 4), (4, 1), (2, 3), (3, 2)}
n(C) = 4
∴ P(C) = \(\frac{4}{36}\)
माना कि 'योग 6 प्राप्त करना' घटना D है
D = {(1, 5), (5, 1), (2, 4), (4, 2), (3, 3)}
n(D) = 5
∴ P(D) = \(\frac{5}{36}\)
माना कि 'योग 7 प्राप्त करना' घटना E है
E = {(1, 6), (6, 1), (2, 5), (5, 2), (4, 3), (3, 4)}
∴ P(E) = P (योग 7 प्राप्त करना) = \(\frac{6}{36}\)
जब दोनों पासों को फेंका जाता है तो 
माना कि 'योग 8 प्राप्त करना' घटना F है।
F = {(2, 6), (6, 2), (3, 5), (4, 4), (5, 3)}
∴ n(F) = 5
∴ P(F) = P(योग 8 प्राप्त करना) = \(\frac{5}{36}\)
माना कि 'योग 9 प्राप्त करना' घटना G है
G = {(4, 5), (5, 4), (3, 6), (6, 3)}
n(G) = 4
∴ P(G) = P(योग 9 प्राप्त करना) = \(\frac{4}{36}\)
माना कि 'योग 10 प्राप्त करना' घटना H है
H = {(6, 4), (4, 6), (5, 5)}
n(H) = 3
∴ P(H) = P(योग 10 प्राप्त करना) = \(\frac{3}{36}\)
माना कि 'योग 11 प्राप्त करना' घटना I है
I = {(5, 6), (6, 5)}
n(I) = 2
∴ P(I) = \(\frac{2}{36}\)
माना कि 'योग 12 प्राप्त करना' घटना J है
J = {(6, 6)}
n(J) = 1
∴ P(J) = \(\frac{1}{36}\)

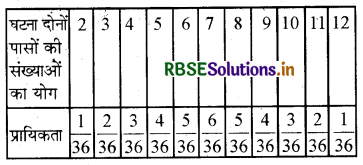
(ii) नहीं सभी 11 सम्भाव्य परिणाम समप्रायिक नहीं हैं। क्योंकि उनकी प्रायिकता भिन्न-भिन्न है।

प्रश्न 23.
एक खेल में एक रुपये के सिक्के को तीन बार उछाला जाता है और प्रत्येक बार का परिणाम लिख लिया जाता है। तीनों परिणाम समान होने पर, अर्थात् तीन चित या तीन पट प्राप्त होने पर, हनीफ खेल में जीत जाएगा, अन्यथा वह हार जाएगा। हनीफ के खेल में हार जाने की प्रायिकता परिकलित कीजिए।
हल-
जब एक रुपये के सिक्के को तीन बार उछाला जाता है तो सम्भाव्य परिणाम हैं:
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
n(S) = 8
माना कि तीनों परिणाम समान होना घटना A है अर्थात् {HHH, TTT}
∴ P(A) = \(\frac{2}{8}=\frac{1}{4}\)
हार जाने की प्रायिकता = 1 - P(A)
P(\(\overline{\mathrm{A}}\)) = 1 - \(\frac{1}{4} = \frac{3}{4}\)
∴ हार जाने की प्रायिकता = \(\frac{3}{4}\)

प्रश्न 24.
एक पासे को दो बार फेंका जाता है। इसकी क्या प्रायिकता है कि
(i) 5 किसी भी बार में नहीं आएगा?
(ii) 5 कम से कम एक बार आएगा?
हल-
जब पासे को दो बार फेंका जाता है तो सभी सम्भाव्य परिणाम हैं :
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n(S) = 36
माना कि '5 प्रत्येक बार 5 आएगा' घटना A है
A = {(1, 5), (2, 5), (3, 5), (4.5), (5, 5), (6, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5)}
n(A) = 11
∴ '5 किसी भी बार नहीं आएगा' घटना \(\overline{\mathrm{A}}\) है
n(\(\overline{\mathrm{A}}\)) = 36 - 11 = 25
(i) ∴ '5 किसी भी बार में नहीं आएगा' की प्रायिकता = \(\frac{25}{36}\)
P(\(\overline{\mathrm{A}}\)) = \(\frac{25}{36}\)
(ii) '5 कम से कम एक बार आएगा' की प्रायिकता = \(\frac{11}{36}\)
∴ P(A) =\( \frac{11}{36}\)

प्रश्न 25.
निम्नलिखित में से कौनसे तर्क सत्य हैं और कौनसे तर्क असत्य हैं? सकारण उत्तर दीजिए:
(i) यदि दो सिक्कों को एक साथ उछाला जाता है, तो इसके तीन सम्भावित परिणाम-दो चित, दो पट या प्रत्येक एक बार हैं। अतः, इनमें से प्रत्येक परिणाम की प्रायिकता \(\frac{1}{3}\) है।
(ii) यदि एक पासे को फेंका जाता है, तो इसके दो सम्भावित परिणाम-एक विषम संख्या या एक सम संख्या हैं। अतः एक विषम संख्या ज्ञात करने की प्रायिकता \(\frac{1}{2}\) है।
हल-
(i) जब दो सिक्कों को उछाला जाता है, तो सम्भाव्य परिणाम हैं :
S = {HH, HT, TH, TT}
दो चित प्राप्त करने की प्रायिकता = \(\frac{1}{4}\)
P(HH) = \(\frac{1}{4}\)
दो पट प्राप्त करने की प्रायिकता =\( \frac{1}{4}\)
P(TT) = \(\frac{1}{4}\)
एक चित और एक पट प्राप्त करने की प्रायिकता = \(\frac{2}{4} = \frac{1}{2}\)
∴ दिया गया तर्क असत्य है।

(ii) जब पासे को फेंका जाता है तो सम्भाव्य परिणाम हैं :
S = {1, 2, 3, 4, 5, 6}
n(S) = 6
∴ विषम संख्याएँ हैं : 1, 3, 5
∴ विषम संख्या प्राप्त करने की प्रायिकता = \(\frac{3}{6}=\frac{1}{2}\)
सम संख्याएँ हैं : 2, 4, 6
∴ सम संख्या प्राप्त करने की प्रायिकता = \(\frac{3}{6}=\frac{1}{2}\)
अतः तर्क सत्य है।