RBSE Solutions for Class 10 Maths Chapter 15 Probability Ex 15.1

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 15 Probability Ex 15.1 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 15 Probability Ex 15.1

Question 1.
Complete the following statements:
(i) Probability of an event E + Probability of the event ‘not E' = __________
(ii) The probability of an event that cannot happen is __________. Such an event is called __________
(iii) The probability of an event that is certain to happen is __________. Such an event is called __________
(iv) The sum of the probabilities of all the elementary events of an experiment is __________
(v) The probability of an event is greater than or equal to __________ and less than or equal to __________
Solution:
(i) 1
(ii) 0, impossible event
(iii) 1, sure or certain event
(iv) 1
(v) 0, 1

Question 2.
Which of the following experiments have equally likely outcomes? Explain.
(i) A driver attempts to start a car. The car starts or does not start.
(ii) A player attempts to shoot a basketball. She/he shoots or misses the shot.
(iii) A trial is made to answer a true-false question. The answer is right or wrong.
(iv) A baby is bom. It is a boy or a girl.
Answer:
(i) When a driver attempts to start a car, then in a normal case the car gets started but if the car has a fault, then the car does not start. Therefore the outcomes are not equally likely.
(ii) When a player attempts to shoot a basketball, then in this case the outcomes are not equally likely since the outcome depends on several facts. For example, the training of players, and the nature of the gun being used in the experiment.
(iii) There are two possibilities for a question - true or false. In this experiment on this question of true or false, only one outcome is possible: true or false i.e. there is only one occasion of the happening of this event, hence the two outcomes are equally likely.
(iv) A newly bom baby (who has taken birth instantly) may be a boy or may be a girl and both the outcomes are equally likely.

Question 3.
Why is tossing a coin considered to be a fair way of deciding which team should get the ball at the beginning of a football game?
Solution:
When a coin is tossed then there are only two possibilities i.e. both the outcomes head or tail are equally likely. So the result of an individual coin toss is completely unpredictable.

Question 4.
Which of the following cannot be the probability of an event?
(A) \(\frac{2}{3}\)
(B) -1.5
(C) 15%
(D) 0.7
Solution:
We know that the probability of an event cannot be less than 0 and more than 1
i.e., 0 ≤ P(E) ≤ 1
∴ (B) -1.5 is impossible.

Question 5.
If P(E) = 0.05, what is the probability of ‘not E’?
Solution:
We know that P(E) + \(\mathbf{P}(\overline{\mathrm{E}})\) = 1
\(\mathbf{P}(\overline{\mathrm{E}})\) = 1 - P(E)
= 1 - 0.05
= 0.95

Question 6.
A bag contains lemon flavoured candies only. Malini takes out one candy without looking into the bag. What is the probability that she takes out
(i) an orange flavoured candy?
(ii) a lemon flavoured candy?
Solution:
(i) Since a bag contains lemon flavoured candies only, therefore there is no orange flavoured candy here.
Hence, it is an impossible event.
∴ Probability of an orange flavoured candy = 0.

(ii) Since in the bag there are only lemon flavoured candies, therefore, it is a sure event.
∴ Probability of a lemon flavoured candy = \(\frac{1}{1}\) = 1

Question 7.
It is given that in a group of 3 students, the probability of 2 students not having the same birthday is 0.992. What is the probability that the 2 students have the same birthday?
Solution:
Let E be the event that the 2 students do not have the same birthday.
∴ E is the event that the 2 students do not have the same birthday.
∴ \(\mathbf{P}(\overline{\mathrm{E}})\) = 0.992
∴ P(E) = 1 - \(\mathbf{P}(\overline{\mathrm{E}})\)
∵ P(E) + \(\mathbf{P}(\overline{\mathrm{E}})\) = 1
= 1 - 0.992
= 0.008
∴ The probability that the 2 students have the same birthday is 0.008.

Question 8.
A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is (i) red? (ii) not red?
Solution:
Number of red balls = 3
Number of black balls = 5
Total number of balls = 3 + 5 = 8
A ball is drawn at random.
(i) Probability that the ball drawn is red = \(\frac {Number of favourable outcomes}{Total number of outcomes}\)
P(red ball) = \(\frac{3}{8}\)

(ii) Probability that the ball drawn is not red = 1 - P(red ball)
= 1 - \(\frac{3}{8}\)
= \(\frac{5}{8}\) [∵ \(P(\bar{E})\) = 1 - P(E)]

Question 9.
A box contains 5 red marbles, 8 white marbles, and 4 green marbles. One marble is taken out of the box at random. What is the probability that the marble is taken out will be (i) red? (ii) white? (iii) not green?
Solution:
Number of red marbles = 5
Number of white marbles = 8
Number of green marbles = 4
Total number of marbles = 5 + 8 + 4 = 17
One marble is taken out.
(i) There are 5 red marbles.
Probability of taking out red marble = \(\frac{Number of favourable outcomes}{Total number of outcomes}\) = \(\frac{5}{17}\)

(ii) There are 5 white marbles.
Probability of taking out white marble = \(\frac{Number of favourable outcomes}{Total number of outcomes}\) = \(\frac{8}{17}\)

(iii) There are 4 green marbles.
Probability of taking out green marble = \(\frac{Number of favourable outcomes}{Total number of outcomes}\) = \(\frac{4}{17}\)
∴ The probability that the marble is taken out is not green = 1 - Probability that the marble is taken out is green
= 1 - \(\frac{4}{17}\)
= \(\frac{13}{17}\)

Question 10.
A piggy bank contains hundred 50p coins, fifty ₹ 1 coin, twenty ₹ 2 coins, and ten ₹ 5 coins. If it is equally likely that one of the coins will fall out when the bank is turned upside down, what is the probability that the coin (i) will be a 50p coin? (ii) will not be an Rs. 5 coins?
Solution:
Number of 50p coins = 100
Number of ₹ 1 coins = 50
Number of ₹ 2 coins = 20
Number of ₹ 5 coins = 10
∴ Total number of coins = 100 + 50 + 20 + 10 = 180
(i) There are 100 coins of 50p.
∴ Probability of getting a ₹ 50p coin = \(\frac{Number of favourable outcomes}{Total number of outcomes}\)
= \(\frac{100}{180}\)
= \(\frac{5}{9}\)

(ii) Number of ₹ 5 coins = 10
∴ Probability of getting a ₹ 5 coins = \(\frac{Number of favourable outcomes}{Total number of outcomes}\)
= \(\frac{10}{180}\)
= \(\frac{1}{18}\)
∴ Probability of not getting a ₹ 5 coins = 1 - P (₹ 5 coins)
= 1 - \(\frac{1}{18}\)
= \(\frac{17}{18}\)

Question 11.
Gopi buys a fish from a shop for his aquarium. The shopkeeper takes out one fish at random from a tank containing 5 male fish and 8 female fish (see Fig. 15.4). What is the probability that the fish taken out is a male fish?

Solution:
Number of male fish = 5
Number of female fish = 8
Total number of fishes in the aquarium = 5 + 8 = 13
Probability that the fish taken out is a male fish = \(\frac{Number of favourable outcomes}{Total number of outcomes}\) = \(\frac{5}{13}\)

Question 12.
A game of chance consists of spinning an arrow that comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (see Fig.), and these are equally likely outcomes. What is the probability that it will point at
(i) 8?
(ii) an old number?
(iii) a number greater than 2?
(iv) a number less than 9?

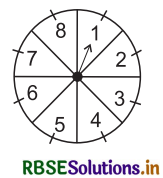
Solution:
(i) Total number of outcomes = {1, 2, 3, 4, 5, 6, 7, 8}
∴ Probability of getting ‘8’ = \(\frac{1}{8}\)

(ii) Odd numbers are = {1, 3, 5, 7}
∴ Probability of getting an odd number = \(\frac{4}{8}=\frac{1}{2}\)

(iii)    The numbers greater than 2 are = (3, 4, 5, 6, 7, 8)
∴ Probability of getting a number greater than 2 = \(\frac{6}{8}=\frac{3}{4}\)
⇒ P(a number greater than 2) = \(\frac{3}{4}\)

(iv) Numbers less than 9 are = {1, 2, 3, 4, 5, 6, 7, 8}
∴ Probability of getting a number less than 9 = \(\frac{8}{8}\)
⇒ P (a number less than 9) = 1

Question 13.
A die is thrown once. Find the probability of getting:
(i) a prime number;
(ii) a number lying between 2 and 6;
(iii) an odd number.
Solution:
When a die is thrown once then the possible outcomes are:
S = {1, 2, 3, 4, 5, 6}
(i) Prime Numbers are = {2, 3, 5}
∴ Probability of getting a prime number = \(\frac{3}{6}=\frac{1}{2}\)

(ii) Numbers lving between 2 and 6 are = {3, 4, 5}
∴ Probability of getting a number lying between 2 and 6 = \(\frac{3}{6}=\frac{1}{2}\)

(iii) Odd numbers are = {1, 3, 5}
∴ Probability of getting an odd number = \(\frac{3}{6}=\frac{1}{2}\)
⇒ P (an odd number) = \(\frac{1}{2}\)

Question 14.
One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting:
(i) a king of red colour
(ii) a face card
(iii) a red face card
(iv) the jack of hearts
(v) a spade
(vi) the queen of diamonds.
Solution:
The number of cards in a deck of cards is 52.
(i) There are two kings of red colour i.e. king of heart and king of diamond.
∴ Probability of getting a king of red colour = \(\frac{2}{52}=\frac{1}{26}\)
⇒ P(a king of red colour) = \(\frac{1}{26}\)

(ii) There are 12 face cards i.e., 4 jacks, 4 queens, and 4 kings.
∴ Probability of getting a face card = \(\frac{12}{52}\)
∴ P(a face card) = \(\frac{3}{13}\)

(iii) There are 6 cards of red colour i.e., 2 jacks, 2 queens and 2 kings.
∴ Probability of getting a red face card = \(\frac{6}{52}\)
⇒ P(a red face card) = \(\frac{3}{26}\)

(iv) There is only one jack of hearts.
∴ Probability of getting a jack of heart = \(\frac{1}{52}\)
⇒ P(The jack of hearts) = \(\frac{1}{52}\)

(v) There are 13 cards of spades.
∴ Probability of getting a card of spades = \(\frac{13}{52}\)
⇒ P(a spade) = \(\frac{1}{4}\)

(vi) There is only one queen of diamonds.
∴ Probability of getting a queen of diamonds = \(\frac{1}{52}\)
⇒ P(The queen of diamonds) = \(\frac{1}{52}\)

Question 15.
Five cards - the ten, jack, queen, king, and ace of diamonds, are well-shuffled with their face downwards. One card is then picked up at random.
(i) What is the probability that the card is the queen? 
(ii) If the queen is drawn and put aside, what is the probability that the second card picked up is (a) an ace? (b) a queen?
Solution:
Five cards are - the ten, jack, queen, king, and ace of diamonds.
(i) Probability of getting a queen = \(\frac{1}{5}\)
∴ P(a queen) = \(\frac{1}{5}\)
(ii) If the queen is drawn and put aside, then four cards are left:
The ten, jack, king, and ace of diamonds
(a) Probability of getting an ace = \(\frac{1}{4}\)
⇒ P(an ace) = \(\frac{1}{4}\)
(b) Probability of getting a queen = \(\frac{0}{4}\) = 0
⇒ P(a queen) = 0

Question 16.
12 defective pens are accidentally mixed with 132 good ones. It is not possible to just look at a pen and tell whether or not it is defective. One pen is taken out at random from this lot. Determine the probability that the pen is taken out is a good one.
Solution:
Number of defective pens = 12
Number of good pens = 132
Total number of pens = 12 + 132 = 144
Probability of getting a good pen = \(\frac{132}{144}=\frac{11}{12}\)
⇒ P(a good pen) = \(\frac{11}{12}\)

Question 17.
(i) A lot of 20 bulbs contain 4 defective ones. One bulb is drawn at random from the lot. What is the probability that this bulb is defective?
(ii) Suppose the bulb drawn in (i) is not defective and is not replaced. Now one bulb is drawn at random from the rest. What is the probability that this bulb is not defective?
Solution:
(i) Number of defective bulbs = 4
Number of good (not defective) bulbs = 16
∴ Total number of bulbs = 4 + 16 = 20
∴ Probability of getting a defective bulb = \(\frac{4}{20}=\frac{1}{5}\)

(ii) When the bulbs drawn are not mixed again with the bulbs, then these remain 19 bulbs.
When the bulbs drawn are not mixed again with the bulbs, then there remain 19 bulbs.
Now the probability of getting a defective bulb = \(\frac{4}{19}\)
So the probability of not getting a defective bulb = 1 - \(\frac{4}{19} = \frac{15}{19}\)
∴ P(not a defective bulb) = \(\frac{15}{19}\)

Question 18.
A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn at random from the box, find the probability that it bears
(i) a two-digit number
(ii) a perfect square number
(iii) a number divisible by 5.
Solution:
(i) There are 90 numbers in all from 1 to 90 and there are 81 two-digit numbers from 10 to 90.
Probability of getting a two-digit number = \(\frac{81}{90}\)
∴ P(a two-digit number) = \(\frac{81}{90}=\frac{9}{10}\)

(ii) Perfect square numbers are {1, 4, 9, 16, 25, 36, 49, 64, 81}
There are 9 perfect square numbers from 1 to 90.
Probability of getting a perfect square number = \(\frac{9}{90}=\frac{1}{10}\)
⇒ P(a perfect square number) = \(\frac{1}{10}\)

(iii) The numbers divisible by 5 are {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90}
There are 18 numbers divisible by 5.
∴ Probability of getting a number divisible by 5 = \(\frac{18}{90}=\frac{1}{5}\)
∴ Required Probability = \(\frac{1}{5}\)

Question 19.
A child has a die whose six faces show the letters as given below:

The die is thrown once. What is the probability of getting (i) A? (ii) D?
Solution:
Number of faces of a die = 6
S = (A, B, C, D, E, A}
n(S) = 6
(i) Since A is on two faces
∴ Probability of getting A = \(\frac{2}{6}=\frac{1}{3}\)
⇒ P(A) = \(\frac{1}{3}\)

(ii) Since D is marked on only one face
∴ Probability of getting D = \(\frac{1}{6}\)
∴ P(D) = \(\frac{1}{6}\)

Question 20.
Suppose you drop a die at random on the rectangular shown in Figure. What is the probability that it will land inside the circle with a diameter of 1 m?

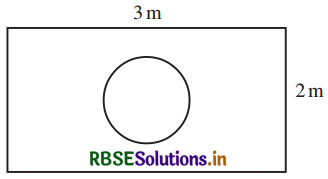
Solution:
Length of rectangle (l) = 3 m
Breadth of rectangle (b) = 2 m
Area of rectangle = 3 m × 2 m = 6m²
Diameter of circle = 1 m
∴ Radius of circle (R) = \(\frac{1}{2}\) m
∴ Area of circle = πR²
= \(\pi\left(\frac{1}{2}\right)^{2}\)
= \(\frac{\pi}{4}\) m²
Probability of a die dropping in a circle = \(\frac {Area of circle}{Area of rectangle}\)
= \(\frac{\frac{\pi}{4} m^{2}}{6 m^{2}}\)
= \(\frac{\pi}{24}\)
∴ Required Probability = \(\frac{\pi}{24}\)

Question 21.
A lot consists of 144 ball pens of which 20 are defective and the others are good. Nuri will buy a pen if it is good, but will not buy it if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that
(i) She will buy it?
(ii) She will not buy it?
Solution:
Total number of ball pens in the lot = 144
Number of defective pens = 20
∴ Number of good pens = 144 - 20 = 124
(i) Let the event of purchasing that pen be A.
∴ Probability of purchasing the pen = \(\frac{124}{144}\)
⇒ P(A) = \(\frac{31}{36}\)

(ii) The event of not purchasing that pen will be \(\overline{\mathrm{A}}\):
⇒ \(P(\bar{A})\) = 1 - P(A)
= 1 - \(\frac{31}{36}\)
= \(\frac{5}{36}\)
∴ P(She will not buy it) = \(\frac{5}{36}\)

Question 22.
Refer to Example 13
(i) Complete the following table:

(ii) A student argues that 'there are 11 possible outcomes 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. Therefore, each of them has probability \(\frac{1}{11}\).' Do you agree with this argument? Justify your answer.
Solution:
(i) When two dice are thrown then the total number of possible outcomes are:
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n{S) = 36
Let A be event of ‘getting a sum 3’.
∴ A = {(1, 2), (2, 1)}
n{A) = 2
∴ Probability of getting a sum 3 = \(\frac{2}{36}\)
⇒ P(A) = \(\frac{2}{36}\)
Let B be the event of ‘getting a sum 4’.
B = {(1, 3), (3, 1), (2, 2)}
n(B) = 3
∴ P(B) = \(\frac{3}{36}\)
Let C be the event of ‘getting a sum 5’.
C = {(1, 4), (4, 1), (2, 3), (3, 2)}
n(C) = 4
∴ P(C) = \(\frac{4}{36}\)
Let D be the event of ‘getting a sum 6’.
D = {(1, 5), (5, 1), (2, 4), (4, 2), (3, 3)}
n(D) = 5
∴ P(D) = \(\frac{5}{36}\)
Let E be the event of ‘getting a sum 7’.
E = {(1, 6), (6, 1), (2, 5), (5, 2), (4, 3), (3, 4)}
∴ P(E) = P(getting a sum 7) = \(\frac{6}{36}\)
Let F be the event of ‘getting a sum 8’.
F = {(2, 6), (6, 2), (3, 5), (4, 4), (5, 3)}
∴ n(F) = 5
∴ P(F) = P(getting a sum 8) = \(\frac{5}{36}\)
Let G be the event of ‘getting a sum 9’.
G = {(4, 5), (5, 4), (3, 6), (6, 3)}
∴ n(G) = 4
∴ P(G) = P(getting a sum 9) = \(\frac{4}{36}\)
Let H be the event of ‘getting a sum 10’.
H = {(6, 4), (4, 6), (5, 5)}
∴ n(H) = 3
∴ P(H) = P(getting a sum 10) = \(\frac{3}{36}\)
Let I be the event of ‘getting a sum 11’.
I = {(5, 6), (6, 5)}
∴ n(I) = 2
∴ P(I) = \(\frac{2}{36}\)
Let J be the event of ‘getting a sum 12’.
J = {(6, 6)}
∴ n(J) = 1
∴ P(J) = \(\frac{1}{36}\)

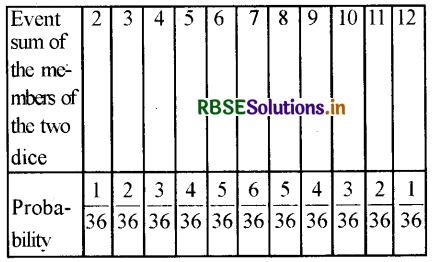
(ii) No, all the eleven possible outcomes are not equally likely since their probabilities are different.

Question 23.
A game consists of tossing a one rupee coin 3 times and noting its outcome each time. Hanif wins if all the tosses give the same result i.e., three heads or three tails, and loses otherwise. Calculate the probability that Hanif will lose the game.
Solution:
When a one rupee coin is tossed three times then the possible outcomes are:
S= {HHH, HHT, HTH, THH, HIT, THT, TTH, TTT}
Let A be event that the three outcomes are the same i.e. {HHH, TTT}
∴ P(A) = \(\frac{2}{8}=\frac{1}{4}\)
Probability of losing = 1 - P(A)
⇒ \(P(\overline{\mathrm{A}}) = 1 - \frac{1}{4} = \frac{3}{4}\)
Probability of losing = \(\frac{3}{4}\)

Question 24.
A die is thrown twice. What is the probability that
(i) 5 will not come up either time?
(ii) 5 will come up at least once?
[Hint: Throwing a die twice and throwing two dice simultaneously are treated as the same experiment]
Solution:
When a die is thrown twice, then all possible outcomes are:
S = {(1, 1), (1, 2), (1. 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n(S) = 36
Let A be the event of '5 coming up each time'.
A = {(1, 5), (2, 5), (3, 5), (4, 5), (5, 5), (6, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5)}
n(A) = 11
∴ \(\overline{\mathrm{A}}\) is the event of '5 will not come up either time’.
\(n(\overline{\mathrm{A}})\) = 36 - 11 = 25
(i) Probability that ‘5 will not come up either time' = \(\frac{25}{36}\)
⇒ \(P(\bar{A}) = \frac{25}{36}\)
(ii) Probability that '5 will come up at least once' = \(\frac{11}{36}\)
∴ P(A) = \(\frac{11}{36}\)

Question 25.
Which of the following arguments are correct and which are not correct? Give reasons for your answer.
(i) If two coins are tossed simultaneously there are three possible outcomes - two heads, two tails, or one of each. Therefore, for each of these outcomes, the probability is \(\frac{1}{3}\).
(ii) If a die is thrown, there are two possible outcomes - an odd number or an even number. Therefore, the probability of getting an odd number is \(\frac{1}{2}\).
Solution:
(i) When two coins arc tossed, then the possible outcomes are:
S = {HH, HT, TH, TT}
Probability of getting two heads = \(\frac{1}{4}\)
⇒ P(HH) = \(\frac{1}{4}\)
Probability of getting two tails = \(\frac{1}{4}\)
⇒ P(TT) = \(\frac{1}{4}\)
Probability of getting one head and one tail = \(\frac{2}{4}=\frac{1}{2}\)
∴ The given argument is incorrect.

(ii) When the die is thrown, then the possible outcomes are:
S = {1, 2, 3, 4, 5, 6}
n(S) = 6
Odd numbers are 1, 3, 5
∴ Probability of getting on odd number = \(\frac{3}{6}=\frac{1}{2}\)
Even numbers are 2, 4, 6
∴ Probability of getting an even number = \(\frac{3}{6}=\frac{1}{2}\)
Hence the argument is correct.