RBSE Solutions for Class 10 Maths Chapter 14 सांख्यिकी Ex 14.4

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 14 सांख्यिकी Ex 14.4 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 14 सांख्यिकी Ex 14.4

प्रश्न 1.
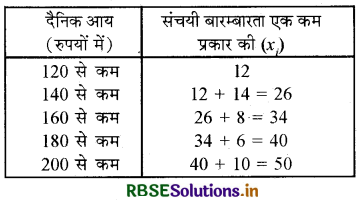
निम्नलिखित बंटन किसी फैक्टरी के 50 श्रमिकों की दैनिक आय दर्शाता है :

'उपर्युक्त बंटन को एक कम प्रकार' के संचयी बारम्बारता बंटन में बदलिए और उसका तोरण खींचिए।
हल-
'से कम' प्रकार का संचयी बारम्बारता बंटन

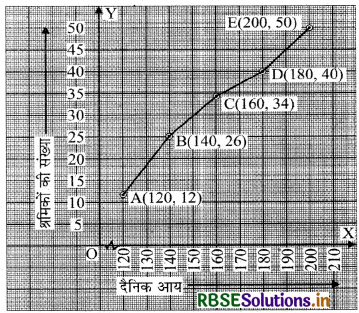
(i) हम सभी बिन्दुओं को अर्थात् A(120, 12); B(140, 26); C(160, 34); D(180, 40); E(200, 50) का ग्राफ पेपर पर आलेखित करते हैं।
(ii) अंकित बिन्दुओं को वक्र के रूप में हाथ से जोड़कर तोरण प्राप्त करते हैं।
हम 'से कम' प्रकार के संचयी बारम्बारता बंटन का ग्राफ प्राप्त करते हैं।
पैमाना : x-अक्ष पर मात्रक 1 cm = रु. 10
तथा y-अक्ष 1 cm = 5 श्रमिक

प्रश्न 2.
किसी कक्षा के 35 विद्यार्थियों की मेडिकल जाँच के समय, उनके भार निम्नलिखित रूप में रिकार्ड किए गए :

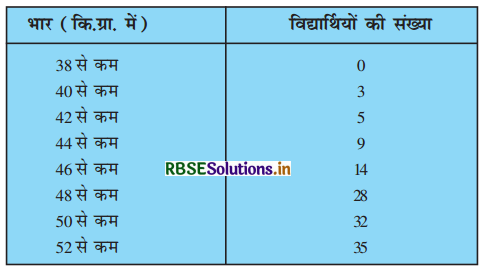
उपर्युक्त आँकड़ों के लिए 'कम प्रकार का तोरण' खींचिए। इसके बाद माध्यक भार ज्ञात कीजिए।
हल-
'से कम' प्रकार का बंटन-

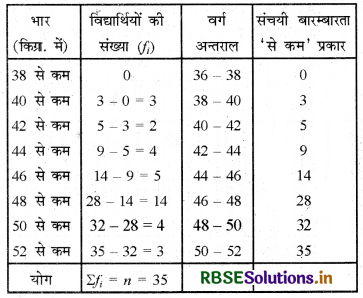
अब, आलेख पर बिन्दुओं अर्थात A(38, 0); B(40, 3); C(42, 5); D(44, 9); E(46, 14); F(48, 28); G(50, 32); H(52, 35)
आलेखित करने पर हमें से कम' प्रकार की संचयी बारम्बारता बहुभुज प्राप्त होता है।
अतः ABCDEFGH अभीष्ट तोरण है।
पैमाना: x-अक्ष पर 1 cm = 2 किग्रा
तथा y-अक्ष पर 1 cm = 5 विद्यार्थी

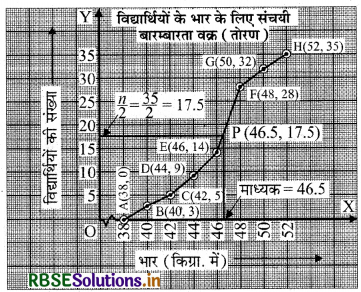
उपर्युक्त आलेख से, यह स्पष्ट है कि
माध्यक = 46.5 किग्रा. जो कि अन्तराल 46 - 48 में स्थित है
अब, दी गई सारणी के अनुसार,
Σfi = n = 35
\(\frac{n}{2}=\frac{35}{2} = 17.5\), जो कि अन्तराल 46 - 48 में स्थित है।
∴ माध्यक वर्ग = 46 - 48
इसलिए l = 46; n = 35; f = 14; cf = 14 और h = 2

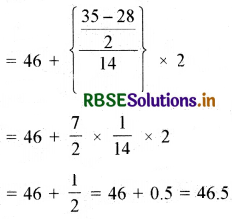
उपर्युक्त ग्राफ से यह स्पष्ट है कि दोनों स्थितियों में माध्यक एक समान ही है।
अतः, विद्यार्थियों का माध्यक भार 46.5 किग्रा. है।

प्रश्न 3.
निम्नलिखित सारणी किसी गाँव के 100 फार्मों में हुआ प्रति हैक्टेयर (ha) गेहूँ का उत्पादन दर्शाते हैं :

इस बंटन को अधिक के प्रकार' के बंटन में बदलिए और फिर उसका तोरण खींचिए।
हल-
दिये गये बंटन को ‘से अधिक' प्रकार के बंटन में बदलना-

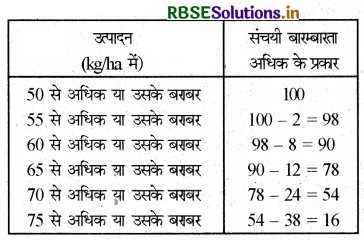
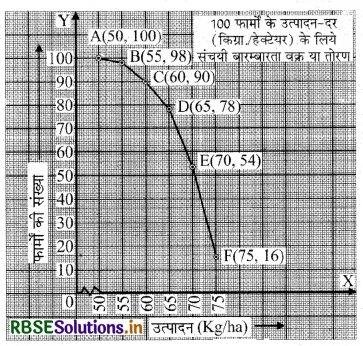
अब, हम बिन्दुओं अर्थात् A(50, 100); B(55, 98); C(60, 90); D(65, 78); E(70, 54); F(75, 16) को ग्राफ पेपर पर आलेखित करते हैं।
हम ‘से अधिक के प्रकार' की संचयी बारम्बारता का ग्राफ प्राप्त करते हैं।
अतः ABCDEF अभीष्ट तोरण है।
पैमाना: x-अक्ष पर 1 cm = 5 kg/ha
तथा y-अक्ष पर 1 cm = 10 फार्म