RBSE Solutions for Class 10 Maths Chapter 14 Statistics Ex 14.4

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 14 Statistics Ex 14.4 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 14 Statistics Ex 14.4

Question 1.
The following distribution gives the daily income of 50 workers of a factory.

Convert the distribution above to a less than type cumulative frequency distribution, and draw its ogive.
Solution:
Cumulative Frequency Distribution of the ‘less than’ Type

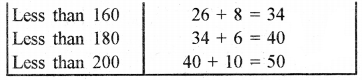
(i) We plot all the points A(120, 12); B(140, 26); C(160, 34); D(180, 40); E(200, 50) on a graph paper.
(ii) Joining the plotted points by a free hand smooth curve we get a cumulative frequency curve or an ogive.
We get the graph of the cumulative frequency distribution of the 'less than' type.
Scale:
On x-axis unit 1 cm = Rs. 10
and on y-axis 1 cm = 5 workers

Question 2.
During the medical check-up of 35 students in a class, their weights were recorded as follows:

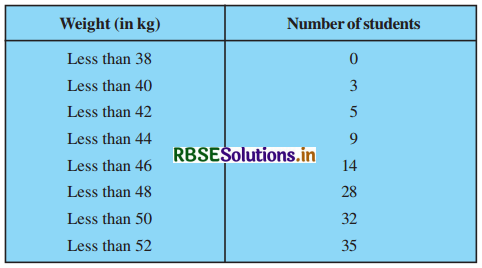
Draw a less than type ogive for the given data. Hence obtain the median weight from the graph and verify the result by using the formula.
Solution:
Distribution of ‘less than’ type

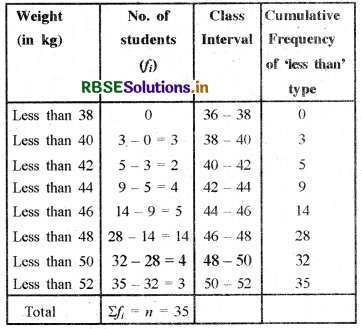
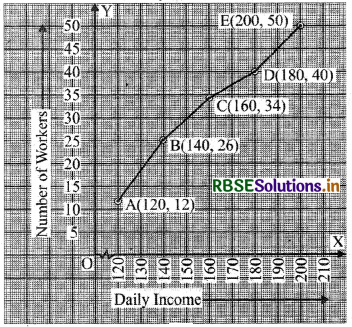
Now, we plot the points i.e., A(38, 0); B(40, 3); C(42, 5); D(44, 9); E(46, 14); F(48, 28); G(50, 32); H(52, 35) on a graph paper and join them by a free hand smooth curve to get cumulative frequency curve. Hence ABCDEFGH is the required ogive.
Scale:
on x-axis 1 cm = 2 kg
and on y-axis 1 cm = 5 students

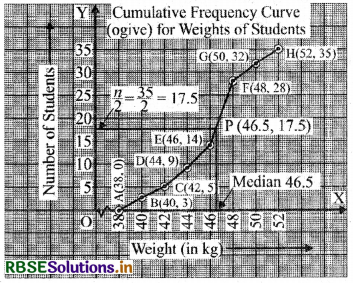
From the above graph, it is clear that the Median = 46.5 kg which lies in the interval 46-48.
Now, according to the given table
Σf_i = n = 35
Then, \(\frac{n}{2}=\frac{35}{2}\) = 17.5, which lies in the interval 46-48.
∴ Median Class = 46 - 48
So, l = 46; n = 35; f = 14; cf = 14 and h = 2

From the above graph, it is clear that in both cases the median is the same.
Hence, the median weight of the students is 46.5 kg.

Question 3.
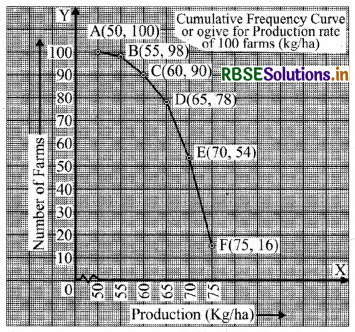
The following table gives the production yield per hectare of wheat of 100 farms in a village.

Change the distribution to a more than type distribution, and draw its ogive.
Solution:
To Convert the given distribution into the distribution of ‘more than’ type

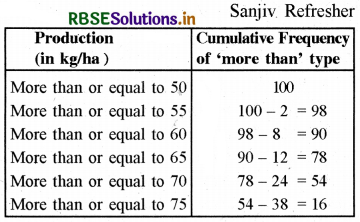
Now, we plot the points, i.e., A(50, 100); B(55, 98); C(60, 90); D(65, 78); E(70, 54); F(75, 16) on a graph paper.
We get the graph of the cumulating frequency of the 'more than type.
Hence ABCDEF is the required ogive.
Scale:
on x-axis is 1 cm = 5 kg/ha
and on y-axis is 1 cm = 10 farms