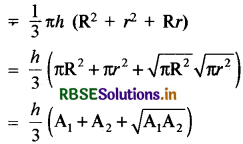RBSE Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes Ex 13.5

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes Ex 13.5 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.5

Use π = \(\frac {22}{7}\), unless stated otherwise.

Question 1.
A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88 per cm³.
Solution:
According to the question,
Diameter of wire (d) = 3 mm
∴ Radius of wire (r) = \(\frac{3}{2}\) mm = \(\frac{3}{20}\) cm
Diameter of cylinder = 10 cm
Radius of cylinder (R) = 5 cm
Height of cylinder (H) = 12 cm

Perimeter of cylinder = Length of wire used in one wrap
⇒ 2πR = Length of wire used in one wrap
⇒ 2 × \(\frac{22}{7}\) × 5 = Length of wire used in one wrap
⇒ \(\frac{220}{7}\) = Length of wire used in one wrap

∴ Length of the wire used = Number of wraps × Length of wire used in one wrap
⇒ H = 40 × \(\frac{220}{7}\) cm = 1257.14 cm
Volume of wire used = πr²H
= \(\frac{22}{7} \times \frac{3}{20} \times \frac{3}{20} \times 1257.14\)
= 88.89 cm³
∵ Mass of 1 cm³ = 8.88 gm
∴ Mass of 88.89 cm³ = 8.88 × 88.89 = 789.41 gm

Question 2.
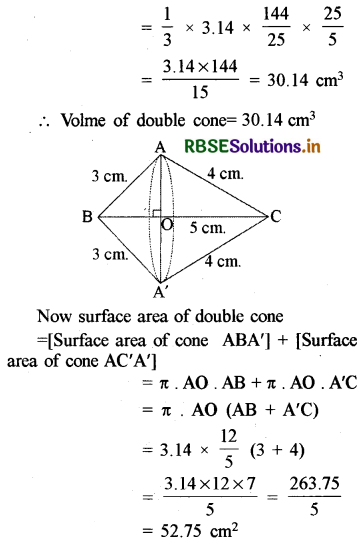
A right triangle, whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose the value of π as found appropriate.)
Solution:
Let ∆ABC be a right-angled triangle at whose A there is a right angle.
The measures of AB and AC are respectively 3 cm and 4 cm.
Length of side BC (hypotenuse) = \(\sqrt{3^{2}+4^{2}}\)
= \(\sqrt{9+16}\)
= 5 cm
Here AO (or A'O) is the radius of the common base of the double-cone obtained by the revolution of the right triangle about side BC.
The height of cone BAA' is BO and the slant height is 3 cm.
The height of the cone CAA' is CO and the slant height is 4 cm.
Now ∆AOB ~ ∆CAB (AA similarity)

Question 3.
A cistern, internally measuring 150 cm × 120 cm × 110 cm, has 129600 cm³ of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being 22.5 cm × 7.5 cm × 6.5 cm?
Solution:
Volume of a brick = 22.5 × 7.5 × 6.5 cm³ = 1096.875 cm³
Volume of cistern = 150 × 120 × 110 cm³ = 1980000 cm³
Let the number of bricks used be = n
Volume of n brides = n (Volume of one brick) = n [1096.875] cm³
Volume of water available for bricks = 1980000 - 129600 = 1850400 cm³
Each brick absorbes \(\frac{1}{17}\)th volume of its volume
∴ Volume of water absorbed by bricks = \(\frac{1}{17}\) × 1096.875 × n = 64.52 × n cm³
∴ 1096.875 × n - 64.52 × n = Volume of water available for bricks
⇒ 1032.355 × n = 1850400
⇒ n = \(\frac{1850400}{1032.355}\) = 1792.41
Hence number of bricks used = 1792

Question 4.
In one fortnight of a given month, there was a rainfall of 10 cm in a river valley. If the area of the valley is 7280 km², show that the total rainfall was approximately equivalent to the addition to the normal water of three rivers each 1072 km long, 75 m wide, and 3 m deep.
Solution:
Volume of each river = L × B × H
= 1072 km × 75 m × 3 m
= 1072 × 1000 × 75 × 3 m³
= 241200000 m³
∴ Volume of total water of these rivers = 3 × 241200000 m³ = 723600000 m³
It is given that area of the valley = 7280 km²
= 7280 × (1000)² m²
= 7280000000 m²
∵ In a river valley the rainfall is 10 cm
∴ Volume of rainfall = 7280000000 × \(\frac{10}{100}\) m³ (∵ 10 cm = \(\frac{10}{100}\) m)
= 728000000 m³
These two volumes must be equal which is not the case.
Hence the facts given in the question are inconsistent.

Question 5.
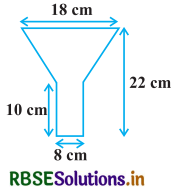
An oil funnel made of the tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, the diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel (see Fig.).

Solution:
According to the question,
Diameter of the upper end of the funnel = 18 cm
∴ Radius of the upper end of the funnel (R) = \(\frac{18}{2}\) cm = 9 cm
Diameter of base of funnel = 8 cm
Radius of base of funnel (r) = 4 cm
Height of the cylindrical portion (h) = 10 cm
Height of the frustum (H) = (22 - 10) = 12 cm

Slant height of frustum (l) = 13 cm
Area of the tin sheet = Curved surface area of the cylindrical base + Curved surface area of the frustum
= 2πrh + πl [R + r]
= 2 × \(\frac{22}{7}\) × 4 × 10 + \(\frac{22}{7}\) × 13 [9 + 4] cm²
= \(\frac{1760}{7}+\frac{3718}{7}\)
= \(\frac{5478}{7}\) cm²
= 782.56 cm²
Hence the total area of the tin sheet used = 782.56 cm² or 782\(\frac{4}{7}\) cm²

Question 6.
Derive the formula for the curved surface area and total surface area of the frustum of a cone, given to you in Section 13.5, using the symbols as explained.
Solution:
We know that frustum of a right circular cone has two unequal circular bases and a curved surface.
Let the frustum obtained by removing part VCD be ACDB.
The line segment joining the centres of both the bases is called the height of the frustum.
Each line segment AC and BD of frustum ACDB is the slant height.

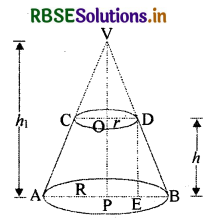
Again let R and r (R > r) be the radii of the circular ends of frustum ACDB of the cone (VAB).
We complete the conical part VCD. Let h and l be respectively the vertical height and the slant height.
Then, OP = h and AC = BD = l
Let the height of the cone VAB be h₁ and slant height be l₁, VP = h₁ and VA = VB = l₁
Now from right angled triangle DEB
DB² = DE² + BE²
l² = h² + (R - r)²
l = \(\sqrt{h^{2}+(\mathrm{R}-r)^{2}}\)
Again ΔVOD ~ ΔVPB

∴ Curved surface area of the frustum of right circular cone = πl (R + r) sq units
where l = \(\sqrt{h^{2}+(\mathrm{R}-r)^{2}}\)
and Total surface area of the frustum of right circular cone = Curved surface area + Area of base + area of upper end
= πl (R + r) + πR² + πr²
= π [R² + r² + l (R + r)] sq units

Question 7.
Derive the formula for the volume of the frustum of a cone, given to you in Section 13.5, using the symbols as explained.
Solution:
We know that the frustum of a right circular cone has two unequal bases and a curved, surface.
Let the frustum ACDB be obtained by removing the part VCD.
The line segment joining the centres of both the bases is called the height of the frustum.
Each line segment AC and BD is the slant height of the frustum ACDB.

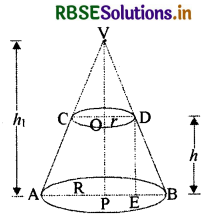
Again, let R and r (R > r) be the radii of the circular ends of the frustum ACDB of the cone (VAB).
We complete the conical part VCD.
Let h and l be respectively the vertical height and the slant height.
Then OP = h and AC = BD = l.
Let the height of cone VAB be h₁ and slant height be l₁
i.e. VP = h₁ and VA = VB = l₁
∴ Height of cone VCD = VP - OP = h₁ - h
∵ Right triangles VOD and VPB are similar

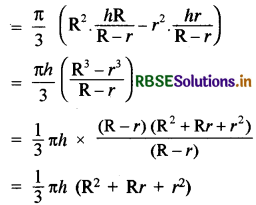
Hence volume of the frustum of cone = \(\frac{1}{3}\) πh (R² + Rr + r²)
Again A₁ and A₂ (A₁ > A₂) be the surface areas of two circular bases
A₁ = πR² and A₂ = πr²
Now the volume of the frustum of the cone