RBSE Solutions for Class 10 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.4

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.4 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.4

जब तक अन्यथा न कहा जाए, π = \(\frac {22}{7}\) लीजिए।

प्रश्न 1.
पानी पीने वाला एक गिलास 14 cm ऊँचाई वाले एक शंकु के छिन्नक के आकार का है। दोनों वृत्ताकार सिरों के व्यास 4 cm और 2 cm हैं। इस गिलास की धारिता ज्ञात कीजिए।
हल-
प्रश्नानुसार,
ऊपरी सिरे की त्रिज्या (R) = 2 cm
निचले सिरे की त्रिज्या (r) = 1 cm
गिलास की ऊँचाई (H) = 14 cm
गिलास छिन्नक के आकार का है

अतः गिलास की धारिता = 102\(\frac{2}{3}\) cm³

प्रश्न 2.
एक शंकु के छिन्नक की तिर्यक ऊँचाई 4 cm है तथा इसके वृत्तीय सिरों के परिमाप (परिधियाँ) 18 cm और 6 cm हैं। इस छिन्नक का वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल-
छिन्नक की तिर्यक ऊँचाई = 4 cm
माना कि ऊपरी सिरे और निचले सिरे की त्रिज्या R और r है।
ऊपरी सिरे की परिधि = 18 cm
∴ 2πR = 18
R = \(\frac{18}{2 \pi}=\frac{9}{\pi}\) cm
निचले सिरे की परिधि = 6 cm
∴ 2πr = 6 cm
r = \(\frac{6}{2 \pi}=\frac{3}{\pi}\) cm
छिन्नक का वक्र पृष्ठीय क्षेत्रफल = π[R + r] l
= \(\pi\left[\frac{9}{\pi}+\frac{3}{\pi}\right] 4\)
= \(\pi\left[\frac{9+3}{\pi}\right] 4\)
= 12 × 4
= 48 cm²
अतः छिन्नक का वक्र पृष्ठीय क्षेत्रफल = 48 cm²

प्रश्न 3.
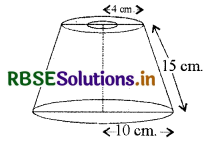
एक तुर्की टोपी शंकु के एक छिन्नक के आकार की है (देखिए आकृति)। यदि इसके खुले सिरे की त्रिज्या 10 cm है, ऊपरी सिरे की त्रिज्या 4 cm है और टोपी की तिर्यक ऊँचाई 15 cm है, तो इसके बनाने में प्रयुक्त पदार्थ का क्षेत्रफल ज्ञात कीजिए।

हल-
प्रश्नानुसार,
छिन्नक के निचले सिरे की त्रिज्या (R) = 10 cm
छिन्नक के ऊपरी सिरे की त्रिज्या (r) = 4 cm
छिन्नक की तिर्यक ऊँचाई (l) = 15 cm
छिन्नक का वक्र पृष्ठीय क्षेत्रफल = πl[R + r]
= \(\frac{22}{7}\) × 15[10 + 4]
= \(\frac{22}{7}\) × 15 × 14
= 22 × 15 × 2
= 660 cm²
बन्द सिरे का क्षेत्रफल = πr²
= \(\frac{22}{7}\) × (4)²
= \(\frac{22}{7}\) × 4 × 4
= \(\frac{352}{7}\) cm²

प्रयुक्त पदार्थ का कुल का क्षेत्रफल = छिन्नक का वक्र पृष्ठीय क्षेत्रफल + बन्द सिरे का क्षेत्रफल
= 660 + \(\frac{352}{7}\)
= \(\frac{4620+352}{7}\)
= \(\frac{4972}{7}\)
= 710\(\frac{2}{7}\) cm²

प्रश्न 4.
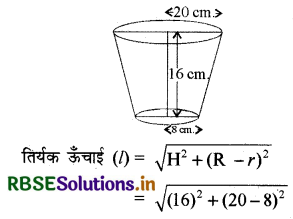
धात की चादर से बना और ऊपर से खुला एक बर्तन शंक के एक छिन्नक के आकार का है, जिसकी ऊँचाई 16 cm है तथा निचले और ऊपरी सिरों की त्रिज्याएँ क्रमशः 8 cm और 20 cm हैं। 20 रु. प्रति लीटर की दर से, इस बर्तन को पूरा भर सकने वाले दूध का मूल्य ज्ञात कीजिए। साथ ही, इस बर्तन को बनाने के लिए प्रयुक्त धातु की चादर का मूल्य 8 रु. प्रति 100 cm की दर से ज्ञात कीजिए। (π = 3.14 लीजिए।)
हल-
प्रश्नानुसार, बर्तन के ऊपरी सिरे की त्रिज्या (R) = 20 cm
बर्तन के निचले सिरे की त्रिज्या (r) = 8 cm
बर्तन की ऊँचाई (H) = 16 cm

∴ बर्तन में दूध का आयतन = 10449.92 cm³ =\(\frac{10449.92}{1000}\) लीटर
∴ बर्तन में दूध का आयतन = 10.45 लीटर
1 लीटर का मूल्य = 20 रु.
∴ 10.45 लीटर का मूल्य = 20 × 10.45
दूध का मूल्य = Rs. 209
छिन्नक का वक्र पृष्ठीय क्षेत्रफल = πl[R + r]
= 3.14 × 20[20 + 8]
= 3.14 × 20 × 28 cm
= 1758.4 cm²
बर्तन के आधार का क्षेत्रफल = πr²
= 3.14 × (8)²
= 3.14 × 64
= 200.96 cm²
बर्तन बनाने के लिए प्रयुक्त धातु = छिन्नक का वक्र पृष्ठीय क्षेत्रफल + आधार का क्षेत्रफल
= (1758.4 + 200.96) cm²
= 1959.36 cm²
∵ 100 cm² धातु की चादर का मूल्य = 8 रु.
∴ 1 cm² धातु की चादर का मूल्य = \(\frac{8}{100}\) रु.
∴ 1959.36 cm² धातु की चादर का मूल्य = \(\frac{8}{100}\) × 1959.36 रु. = 156.748 रु. = 156.75 रु.
अतः दूध का मूल्य = 209 रु.
और चादर का मूल्य = 156.75 रु.

प्रश्न 5.
20 cm ऊँचाई और शीर्ष कोण (vertical angle) 60° वाले एक शंकु को उसकी ऊँचाई के बीचों-बीच से होकर जाते हुए एक तल से दो भागों में काटा गया है, जबकि तल शंकु के आधार के समान्तर है। यदि इस प्राप्त शंकु के छिन्नक को व्यास \(\frac{1}{16}\) cm वाले एक तार के रूप में बदल दिया जाता है तो तार की लम्बाई ज्ञात कीजिए।
हल-
प्रश्नानुसार, शंकु का शीर्ष कोण = 60°
शंकु का शीर्षलम्ब शीर्ष कोण को द्विभाजित करता है।

छिन्नक का आयतन = \(\frac{22}{7} \times 10 \times \frac{700}{9} \)cm³ = \(\frac{22}{7} \times \frac{7000}{9}\) cm³
छिन्नक की तार बनाई गई है जो कि बेलन के आकार की है जिसका व्यास \(\frac{1}{16}\) cm है।
∴ बेलनाकार तार की त्रिज्या (r₁) = \(\frac{1}{2} \times \frac{1}{16} = \frac{1}{32}\) cm
माना कि इस प्रकार बने बेलन की लम्बाई = H cm
∵ रूप बदलने पर भी आयतन समान ही रहता है।
छिन्नक का आयतन = बेलनाकार तार का आयतन

अतः, बेलनाकार तार की लम्बाई (H) = 7964.4 m