RBSE Solutions for Class 10 Maths Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.3

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.3 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.3

(जब तक अन्यथा न कहा जाए, π = \(\frac{22}{7}\) का प्रयोग कीजिए)

प्रश्न 1.
आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि PQ = 24 cm, PR = 7 cm तथा O वृत्त का केन्द्र है।

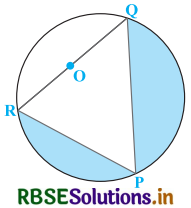
हल-
प्रश्नानुसार, PQ = 24 cm तथा PR = 7 cm
RQ वृत्त का व्यास है।
∠RPQ = 90° अर्द्धवृत्त का कोण
अब ∆PQR में,
QR² = RP² + PQ²
⇒ QR = \(\sqrt{(7)^{2}+(24)^{2}}\)
⇒ QR = \(\sqrt{49+576}\)
⇒ QR = \(\sqrt{625}\)
⇒ QR = 25 cm
∴ वृत्त का व्यास (QR) = 25 cm
अतः वृत्त की त्रिज्या (R) = \(\frac{25}{2}\) cm
छायांकित भाग का क्षेत्रफल = अर्द्धवृत्त का क्षेत्रफल - ∆RPQ का क्षेत्रफल

अतः छायांकित भाग का क्षेत्रफल = \(\frac{4523}{28}\) या 161.53 cm²

प्रश्न 2.
आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि केन्द्र O वाले दोनों संकेन्द्रीय वृत्तों की त्रिज्याएँ क्रमशः 7 cm और 14 cm हैं तथा ∠AOC = 40° है।

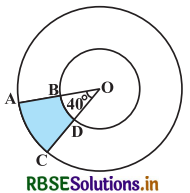
हल-
प्रश्नानुसार,छोटे वृत्त की त्रिज्या (r) = 7 cm
तथा बड़े वृत्त की त्रिज्या (R) = 14 cm
र केन्द्रीय कोण ∠AOC (θ) = 40°
छायांकित भाग का क्षेत्रफल = बड़े वृत्तखण्ड OAC का क्षेत्रफल - छोटे वृत्तखण्ड OBD का क्षेत्रफल
= \(\frac{\pi R^{2} \theta}{360^{\circ}} - \frac{\pi r^{2} \theta}{360^{\circ}}\)
= \(\frac{\pi \theta}{360^{\circ}}\left[\mathrm{R}^{2}-r^{2}\right]\)

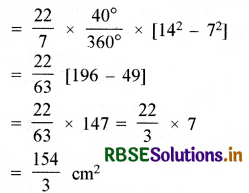
प्रश्न 3.
आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि ABCD भुजा 14 cm का एक वर्ग है तथा APD और BPC दो अर्द्धवृत्त हैं।

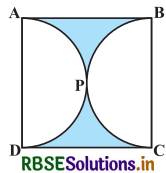
हल-
प्रश्नानुसार, वर्ग की भुजा = 14 cm
∴ अर्द्धवृत्त का व्यास (AD या BC) = 14 cm
अर्द्धवृत्त की त्रिज्या (R) = 7 cm
वर्ग का क्षेत्रफल = (भुजा)²
= 14 × 14
= 196 cm²
∵ अर्द्धवृत्त का क्षेत्रफल = \(\frac{1}{2} \pi \mathrm{R}^{2}\)
= \(\frac{1}{2} \times \frac{22}{7} \times 7 \times 7\)
= 77 cm²
दो अर्द्धवृत्तों का क्षेत्रफल = 2(77) = 154 cm²
छायांकित भाग का क्षेत्रफल = वर्ग ABCD का क्षेत्रफल - दो अर्द्धवृत्तों का क्षेत्रफल
= (196 - 154)
= 42 cm²
∴ छायांकित भाग का क्षेत्रफल = 42 cm²

प्रश्न 4.
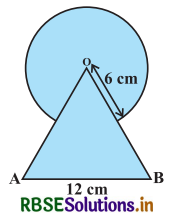
आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, जहाँ भुजा 12 cm वाले एक समबाहु त्रिभुज OAB के शीर्ष O को केन्द्र मानकर 6 cm त्रिज्या वाला एक वृत्तीय चाप खींचा गया है।

हल-
प्रश्नानुसार, चाप की त्रिज्या (R) = 6 cm
समबाहु त्रिभुज OAB की भुजा = 12 cm
OA = OB = AB = 12 cm
त्रिज्यखण्ड का केन्द्रीय कोण = 60°
∵ समबाहु त्रिभुज का प्रत्येक कोण = 60°
∴ वृत्त के दीर्घ त्रिज्यखण्ड का क्षेत्रफल = वृत्त का क्षेत्रफल - त्रिज्यखण्ड का क्षेत्रफल

∴ छायांकित भाग का क्षेत्रफल = समबाहु त्रिभुज का क्षेत्रफल OAB + वृत्त का दीर्घ त्रिज्यखण्ड का क्षेत्रफल = (36√3 + \(\frac{660}{7}\)) cm²

प्रश्न 5.
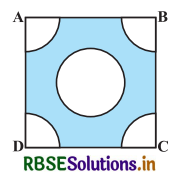
भुजा 4 cm वाले एक वर्ग के प्रत्येक कोने से 1 cm त्रिज्या वाले वृत्त का एक चतुर्थांश काटा गया है तथा बीच में 2 cm व्यास का एक वृत्त भी काटा गया है, जैसा कि आकृति में दर्शाया गया है। वर्ग के शेष भाग का क्षेत्रफल ज्ञात कीजिए।

हल-
प्रश्नानुसार, वर्ग की भुजा = 4 cm
काटे गए प्रत्येक अर्द्धवृत्त की त्रिज्या (r) = 1 cm
वृत्त का व्यास (R) = 2 cm
वृत्त की त्रिज्या (R) = 1 cm
वर्ग का क्षेत्रफल = (भुजा)²
= (4)²
= 16 cm

(∵ बीच वाले वृत्त की त्रिज्या = 1 cm है)
∴ अभीष्ट छायांकित भाग का क्षेत्रफल = वर्ग का क्षेत्रफल - 4 चतुर्थांशों का क्षेत्रफल - वृत्त का क्षेत्रफल

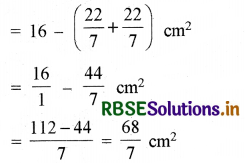
प्रश्न 6.
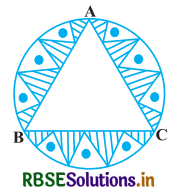
एक वृत्ताकार मेजपोश, जिसकी त्रिज्या 32 cm है, में बीच में एक समबाहु त्रिभुज ABC छोड़ते हुए एक डिजाइन बना हुआ है, जैसा कि आकृति में दिखाया गया है। इस डिजाइन का क्षेत्रफल ज्ञात कीजिए।

हल-
प्रश्नानुसार, मेजपोश की त्रिज्या (R) = 32 cm
OA = OB = OC = 32
∆ABC एक समबाहु त्रिभुज है और O इसके परिवृत्त बने 32 cm की त्रिज्या वाले वृत्त का केन्द्र है।

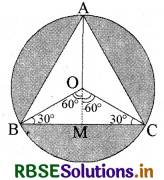
∴ वृत्त का क्षेत्रफल = πr²
= \(\frac {22}{7}\) × 32 × 32 cm²
= \(\frac {22528}{7}\) cm²
∵ ∆ABC समबाहु त्रिभुज है।
∴ ∠B = 60°
OB तथा OC वृत्ताकार मेजपोश की त्रिज्याएँ हैं।
∴ OB = 32 सेमी.
और ∠OBM = \(\frac{1}{2}\) ∠B = 30°
केन्द्र O से OM ⊥ BC खींचा
∴ BM = \(\frac{1}{2}\) BC
BC = 2BM
समकोण ∆OBM में
cos 30° = \(\frac{\mathrm{BM}}{\mathrm{BO}}\)
⇒ \(\frac{\sqrt{3}}{2}=\frac{\mathrm{BM}}{32}\)
⇒ 2BM = 32√3
लेकिन भुजा (BC) = 2(2BM)
∴ भुजा (BC) = 32√3 सेमी.
∴ समबाहु ∆ABC की भुजा = 32√3 सेमी.
∴ समबाहु ∆ABC का क्षेत्रफल
= \(\frac{\sqrt{3}}{4}\) × (भुजा)²
= \(\frac{\sqrt{3}}{4}\) × (32√3)²
= \(\frac{\sqrt{3}}{4}\) × 1024 × 3
= 768√3 वर्ग सेमी.
अतः छायांकित भाग का क्षेत्रफल = मेजपोश का क्षेत्रफल - समबाहु त्रिभुज का क्षेत्रफल = (\(\frac{22528}{7}\) - 768√3) वर्ग सेमी.

प्रश्न 7.
आकृति में, ABCD भुजा 14 cm वाला एक वर्ग है। A, B, C और D को केन्द्र मानकर, चार वृत्त इस प्रकार खींचे गए हैं कि प्रत्येक वृत्त तीन शेष वृत्तों में से दो वृत्तों को बाह्य रूप से स्पर्श करता है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

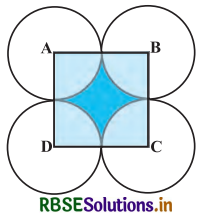
हल-
प्रश्नानुसार, वर्ग ABCD की भुजा = 14 cm
तथा वृत्त की त्रिज्या (R) = 7 cm
त्रिज्यखण्ड कोण (θ) = 90°
वर्ग का क्षेत्रफल = (भुजा)²
= 14 × 14
= 196 cm²
चार चतुर्थांशों का क्षेत्रफल = \(4\left[\frac{\pi \mathrm{R}^{2} \theta}{360^{\circ}}\right]\)
= \(4 \times \frac{22}{7} \times \frac{7 \times 7 \times 90^{\circ}}{360^{\circ}}\)
= 22 × 7
= 154 cm²
∴ अभीष्ट छायांकित क्षेत्रफल = वर्ग का क्षेत्रफल - चार चतुर्थांशों का क्षेत्रफल
= 196 - 154
= 42 cm²

प्रश्न 8.
आकृति एक दौड़ने का पथ (racing track) दर्शाती है, जिसके बाएँ और दाएँ सिरे अर्द्धवृत्ताकार हैं। दोनों आन्तरिक समान्तर रेखाखण्डों के बीच की दूरी 60 m है तथा इनमें से प्रत्येक रेखाखण्ड 106 m लम्बा है। यदि यह पथ 10 m चौड़ा है, तो ज्ञात कीजिए-
(i) पथ के आन्तरिक किनारों के अनुदिश एक पूरा चक्कर लगाने में चली गई दुरी
(ii) पथ का क्षेत्रफल

हल-

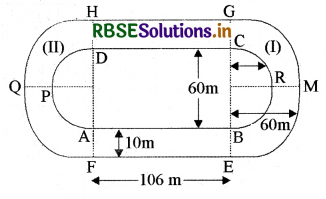
(i) यहाँ AB = DC = 106 m
AF = BE = CG = HD = 10 m
आन्तरिक अर्द्धवृत्त का व्यास = 60 m
∴ अर्द्धवृत्त की आन्तरिक त्रिज्या (r) = 30 m
अर्द्धवृत्त की बाहरी त्रिज्या (R) = r + 10
= 30 + 10
= 40 m
पथ के आन्तरिक किनारों के अनुदिश एक पूरा चक्कर लगाने में चली गई दूरी = AB + अर्द्धवृत्त BRC का परिमाप + CD + अर्द्धवृत्त DPA का परिमाप
= 2AB + 2[अर्द्धवृत्त BRC का क्षेत्रफल]
= 2(106) + \(2\left(\frac{2 \pi r}{2}\right)\) [∵ AB = DC = 106]
= 212 + 2πr
= 212 + 2 × \(\frac {22}{7}\) × 30
= 212 + \(\frac{60 \times 22}{7}\)
= \(\frac{1484+1320}{7}\)
= \(\frac{2804}{7}\) m
(ii) पथ का क्षेत्रफल = आयत ABEF का क्षेत्रफल + क्षेत्र BEMGCRB का क्षेत्रफल + आयत CGHD का क्षेत्रफल + क्षेत्र का क्षेत्रफल
= 2 आयत ABCD का क्षेत्रफल + 2 क्षेत्र का क्षेत्रफल
= 2 (AB × AF) + 2[अर्द्धवृत्त की त्रिज्या 60 cm - अर्द्धवृत्त जिसकी त्रिज्याएँ 30 cm हैं का क्षेत्रफल]

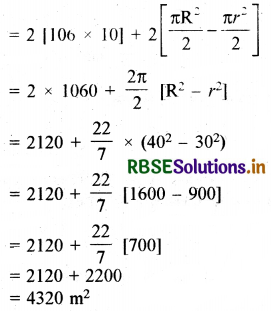
∴ पथ का क्षेत्रफल = 4320 m²

प्रश्न 9.
आकृति में, AB और CD केन्द्र O वाले एक वृत्त के दो परस्पर लम्ब व्यास हैं तथा OD छोटे वृत्त का व्यास है। यदि OA = 7 cm है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

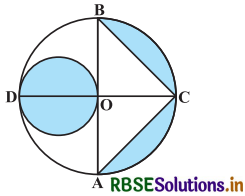
हल-
प्रश्नानुसार, वृत्त का व्यास = 14 cm
∴ वृत्त की त्रिज्या = 7 cm
छोटे वृत्त का व्यास = 7 cm
∴ छोटे वृत्त की त्रिज्या = \(\frac{7}{2}\) cm
AB और CD एक वृत्त के दो परस्पर लम्ब व्यास हैं।
AD ⊥ CD
त्रिज्यखण्ड OCB का क्षेत्रफल = \(\left(\frac{90^{\circ}}{360^{\circ}} \times \frac{22}{7} \times 7 \times 7\right)\) cm²
= \(\frac{1}{4}\) × 22 × 7 cm²
= \(\frac{77}{2}\) cm²
∆OCB का क्षेत्रफल = \(\frac{1}{2}\) × OC × OB
= \(\frac{1}{2}\) × 7 × 7 cm²
= \(\frac{49}{2}\) cm²
∴ वृत्तखण्ड BPC का क्षेत्रफल = \(\left(\frac{77}{2}-\frac{49}{2}\right)\) cm²
= \(\frac{28}{2}\) cm²
= 14 cm²
इसी प्रकार वृत्तखण्ड AQC का क्षेत्रफल = 14 cm²
DO व्यास वाले छोटे वृत्त का क्षेत्रफल = πr²
= \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\)
= \(\frac{77}{2}\) cm²
अतः छायांकित भाग का कुल क्षेत्रफल = (14 + 14 + \(\frac{77}{2}\)) cm²
= \(\left(\frac{28+28+77}{2}\right)\) cm²
= \(\frac{133}{2}\) cm²
= 66.5 cm²

प्रश्न 10.
एक समबाहु त्रिभुज ABC का क्षेत्रफल 17320.5 cm² है। इस त्रिभुज के प्रत्येक शीर्ष को केन्द्र मानकर त्रिभुज की भुजा के आधे के बराबर की त्रिज्या लेकर एक वृत्त खींचा जाता है (देखिए आकृति)। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। (π = 3.14 और √3 = 1.73205 लीजिए।)

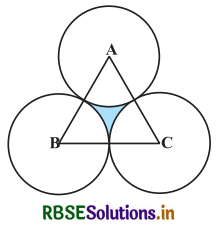
हल-
समबाहु त्रिभुज ABC का क्षेत्रफल = 17320.5 cm²
समबाहु त्रिभुज का क्षेत्रफल = \(\frac{\sqrt{3}}{4}\) × (भुजा)²

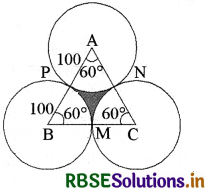
प्रश्नानुसार,
\(\frac{\sqrt{3}}{4}\) (भुजा)² = 17320.5
⇒ (भुजा)² = \(\frac{17320.5 \times 4}{1.73205}\)
⇒ (भुजा)² = \(\frac{173205}{10} \times \frac{100000 \times 4}{173205}\)
⇒ भुजा = \(\sqrt{4 \times 100 \times 100}\)
⇒ भुजा = 2 × 100 = 200 cm
∴ AB = BC = AC = 200 cm [∵ समबाहु त्रिभुज है।]
वृत्त की त्रिज्या (R) = \(\frac{\mathrm{AB}}{2} \)
= \(\frac{200}{2}\)
= 100 cm
त्रिज्यखण्ड का कोण (θ) = 60°
चित्र में तीन त्रिज्यखण्ड हैं।
इसलिये तीनों त्रिज्यखण्डों का क्षेत्रफल = 3 × \(\frac{\pi \mathrm{R}^{2} \theta}{360^{\circ}}\)
= \(\frac{3 \times 3.14 \times 100 \times 100 \times 60^{\circ}}{360^{\circ}}\)
= 3.14 × 50 × 100
= 15700 cm²
∴ अभीष्ट छायांकित क्षेत्रफल = त्रिभुज का क्षेत्रफल - तीन त्रिज्यखण्डों का क्षेत्रफल
= 17320.5 - 15700
= 1620.5 cm²
∴ छायांकित क्षेत्रफल = 1620.5 cm²

प्रश्न 11.
एक वर्गाकार रूमाल पर, नौ वृत्ताकार डिजाइन बने हैं, जिनमें से प्रत्येक की त्रिज्या 7 cm है (देखिए आकृति)। रूमाल के शेष भाग का क्षेत्रफल ज्ञात कीजिए।

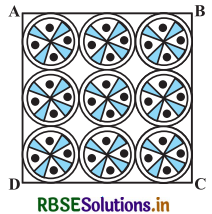
हल-
वृत्त की त्रिज्या (R) = 7 cm
वृत्त का व्यास = 2 × R
= 2 × 7
= 14 cm
क्योंकि वर्ग की भुजा के अनुदिश तीन वृत्त हैं।
∴ वर्ग की भुजा = 3(14) = 42 cm
रूमाल का कुल क्षेत्रफल = वर्ग का क्षेत्रफल = (भुजा)²
= (42)² cm²
= 1764 cm²
नौ वृत्ताकार डिजाइनों का क्षेत्रफल = 9πR²
= 9 × \(\frac {22}{7}\) × (7)²
= 9 × \(\frac {22}{7}\) × 7 × 7
= 9 × 154
= 1386 cm²
∴ शेष भाग का अभीष्ट क्षेत्रफल = वर्ग का क्षेत्रफल - 9 वृत्ताकार डिजाइनों का क्षेत्रफल
= 1764 - 1386
= 378 cm²

प्रश्न 12.
आकृति में, OACB केन्द्र O और त्रिज्या 3.5 cm वाले एक वृत्त का चतुर्थांश है। यदि OD = 2 cm है, तो निम्नलिखित के क्षेत्रफल ज्ञात कीजिए :
(i) चतुर्थांश OACB
(ii) छायांकित भाग

हल-
प्रश्नानुसार, चतुर्थांश की त्रिज्या (R) = 3.5 cm
त्रिज्यखण्ड का कोण (θ) = 90°
OD = 2 cm
(i) चतुर्थांश OACB का क्षेत्रफल = \(\frac{\pi \mathrm{R}^{2} \theta}{360^{\circ}}\)
= \(\frac{22}{7} \times \frac{3.5 \times 3.5 \times 90^{\circ}}{360^{\circ}}\)
= \(\frac{77}{8}\) cm²
(ii) ∆ODB का क्षेत्रफल = \(\frac {1}{2}\) × आधार × ऊँचाई
= \(\frac {1}{2}\) × 3.5 × 2
= 3.5 cm²
∴ छायांकित क्षेत्रफल = चतुर्थांश OACB का क्षेत्रफल - ∆ODB का क्षेत्रफल
= \(\frac{77}{8}\) - 3.5
= \(\frac{49}{8}\) cm²
अतः छायांकित भाग का क्षेत्रफल = \(\frac{49}{8}\) cm² या 6.125 cm²

प्रश्न 13.
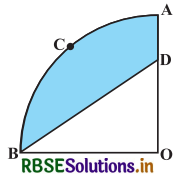
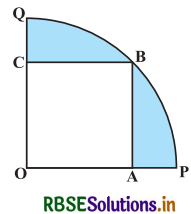
आकृति में, एक चतुर्थांश OPBQ के अन्तर्गत एक वर्ग OABC बना हुआ है। यदि OA = 20 cm है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए।)

हल-
प्रश्नानुसार, वर्ग ABCO की भुजा = 20 cm
∠AOC = 90°
AB = OA

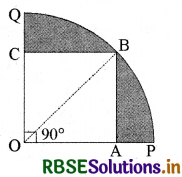
∴ ∆OAB से,
OB² = OA² + AB²
⇒ OB = \(\sqrt{(20)^{2}+(20)^{2}}\)
⇒ OB = \(\sqrt{400+400}\)
⇒ OB = \(\sqrt{800}\)
⇒ OB = 20√2 cm
वर्ग OABC का क्षेत्रफल = (भुजा)² = (20)²
∴ वर्ग का क्षेत्रफल = 400 cm²
चतुर्थांश की त्रिज्या (R) = 20√2
त्रिज्यखण्ड का कोण (θ) = 90°
∴ त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\pi R^{2} \theta}{360^{\circ}}\)
= \(\frac{3.14 \times 20 \sqrt{2} \times 20 \sqrt{2} \times 90^{\circ}}{360^{\circ}}\)
= 2 × 314 cm²
= 628 cm²
∴ अभीष्ट छायांकित क्षेत्रफल = त्रिज्यखण्ड का क्षेत्रफल - वर्ग का क्षेत्रफल
= (628 - 400) cm²
= 228 cm²

प्रश्न 14.
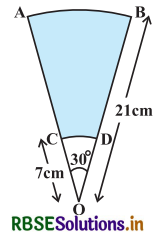
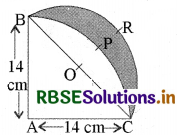
AB और CD केन्द्र O तथा त्रिज्याओं 21 cm और 7 cm वाले दो संकेन्द्रीय वृत्तों के क्रमशः दो चाप हैं (देखिए आकृति)। यदि ∠AOB = 30° है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

हल-
त्रिज्यखण्ड OBA की त्रिज्या (R) = 21 cm
त्रिज्यखण्ड ODC की त्रिज्या (r) = 7 cm
त्रिज्यखण्ड का कोण (θ) = 30°

अब छायांकित भाग का क्षेत्रफल = बड़े त्रिज्यखण्ड OAB का क्षेत्रफल - छोटे त्रिज्यखण्ड OCD का क्षेत्रफल
= \(\frac{231}{2}-\frac{77}{6}\)
= \(\left(\frac{693-77}{6}\right)\)
= \(\frac{616}{6}\)
= \(\frac{308}{3}\) सेमी²
छायांकित भाग का क्षेत्रफल = 102.66 cm²

प्रश्न 15.
आकृति में, ABC त्रिज्या 14 cm. वाले एक वृत्त का चतुर्थांश है तथा BC को व्यास मान कर एक अर्द्धवृत्त खींचा गया है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

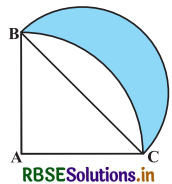
हल-
त्रिज्यखण्ड ACPB की त्रिज्या (r) = 14 cm
त्रिज्यखण्ड कोण (θ) = 90°
AB = AC = 7 cm
त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) × AB × AC
= \(\frac{1}{2}\) × 14 × 14
= 98 cm²

त्रिज्यखण्ड ACPB का क्षेत्रफल = \(\frac{\pi r^{2} \theta}{360^{\circ}}\)
= \(\frac{22}{7} \times \frac{14 \times 14 \times 90^{\circ}}{360^{\circ}}\)
= 154 cm²
∴ BOCPB का क्षेत्रफल = त्रिज्यखण्ड ABPC का क्षेत्रफल - ΔABC का क्षेत्रफल
= 154 cm² - 98 cm²
= 56 cm²
ΔBAC में,
AB² + AC² = BC²
(14)² + (14)² = BC²
BC = \(\sqrt{196+196}\)
= \(\sqrt{2(196)}\)
= 14√2
∴ अर्द्धवृत्त BOCR की त्रिज्या = \(\frac{14 \sqrt{2}}{2}\) = 7√2
अर्द्धवृत्त का क्षेत्रफल = \(\frac{\pi \mathrm{R}^{2}}{2}\)
= \(\frac{22}{7} \times \frac{7 \sqrt{2} \times 7 \sqrt{2}}{2}\)
= 154 cm²
अभीष्ट क्षेत्रफल = अर्द्धवृत्त का क्षेत्रफल - [त्रिज्यखण्ड का क्षेत्रफल - ΔBAC का क्षेत्रफल]
= 154 - [154 - 98]
= 154 - 56
= 98 cm²
छायांकित भाग का क्षेत्रफल = 98 cm²

प्रश्न 16.
आकृति में, छायांकित डिजाइन का क्षेत्रफल ज्ञात कीजिए, जो 8 cm त्रिज्याओं वाले दो वृत्तों के चतुर्थांशों के बीच उभयनिष्ठ है।

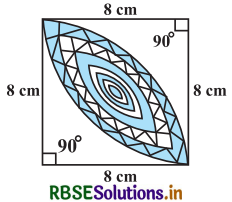
हल-
वर्ग की भुजा = 8 cm
वर्ग का क्षेत्रफल = (8)² = 64 cm
रेखा BD वर्ग ABCD को समान भागों में विभाजित करती है।

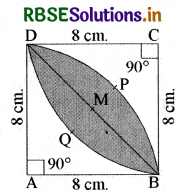
∴ ∆ABD का क्षेत्रफल = ∆BDC का क्षेत्रफल त्रिज्यखण्ड का कोण (θ) = 90°
ABPD त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\pi \mathrm{R}^{2} \theta}{360^{\circ}}\) = \(\frac{22}{7} \times \frac{8 \times 8 \times 90^{\circ}}{360^{\circ}}\)
ABPD त्रिज्यखण्ड का क्षेत्रफल = \(\frac{352}{7}\) cm²
अतः त्रिज्यखण्ड ABPD का क्षेत्र = \(\frac{352}{7}\) cm²
अब ∆ABD का क्षेत्रफल = \(\frac{1}{2}\) × AB × AD
= \(\frac{1}{2}\) × 8 × 8 
= 32 cm²
अत: ABD का क्षेत्रफल = 32 cm²
∴ वृत्तखण्ड DMBPD का क्षेत्रफल = त्रिज्यखण्ड ABPD का क्षेत्रफल - ∆ABD का क्षेत्रफल
= \(\frac{352}{7}-\frac{32}{1}\)
= \(\frac{128}{7}\) cm²
∴ छायांकित भाग का क्षेत्रफल = 2 वृत्तखण्ड DMBPD का क्षेत्रफल
= 2 × \(\frac{128}{7}\) cm²
= \(\frac{256}{7}\) cm²
अतः छायांकित भाग का क्षेत्रफल = \(\frac{256}{7}\) cm²