RBSE Solutions for Class 10 Maths Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.2

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.2 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.2

(जब तक अन्यथा न कहा जाए, π = \(\frac{22}{7}\) का प्रयोग कीजिए)

प्रश्न 1.
6 cm त्रिज्या वाले एक वृत्त के एक त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण 60° है।
हल-
प्रश्नानुसार वृत्त के त्रिज्यखण्ड की त्रिज्या (R) = 6 cm

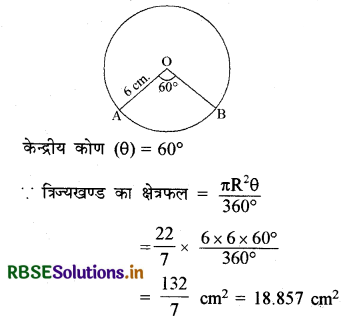
अतः त्रिज्यखण्ड का क्षेत्रफल = \(\frac{132}{7}\) = 18.86 cm (लगभग)

प्रश्न 2.
एक वृत्त के चतुर्थांश (quadrant) का क्षेत्रफल ज्ञात कीजिए, जिसकी परिधि 22 cm है।
हल-
प्रश्नानुसारवृत्त की परिधि = 22 cm
∴ 2πR = 22

अतः इस वृत्त के चतुर्थांश का क्षेत्रफल \(\frac{77}{8}\) cm² होगा।

प्रश्न 3.
एक घड़ी की मिनट की सुई जिसकी लम्बाई 14 cm है। इस सुई द्वारा 5 मिनट में रचित क्षेत्रफल ज्ञात कीजिए।
हल-
प्रश्नानुसार मिनट की सुई की लम्बाई = वृत्त की त्रिज्या (R) = 14 cm
हम जानते हैं कि
60 मिनट = 60' = 360°
1 मिनट = 1' = \(\frac{360}{60}\) = 6°
5 मिनट = 5' = 6° × 5 = 30°
त्रिज्यखण्ड कोण (θ) = 30°
अतः सुई द्वारा 5 मिनट में रचित क्षेत्रफल

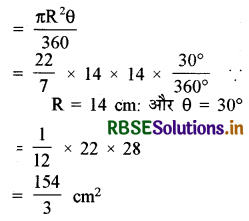
अतः मिनट की सुई द्वारा 5 मिनट में रचित क्षेत्रफल \(\frac{154}{3}\) cm² होगा।

प्रश्न 4.
10 सेमी. त्रिज्या वाले एक वृत्त की कोई जीवा केन्द्र पर एक समकोण अन्तरित करती है। निम्नलिखित के क्षेत्रफल ज्ञात कीजिए :
(i) संगत लघु वृत्तखण्ड
(ii) संगत दीर्घ त्रिज्यखण्ड
(π = 3.14 का प्रयोग कीजिए)
हल-
प्रश्नानुसार, वृत्त की त्रिज्या (R) = 10 cm

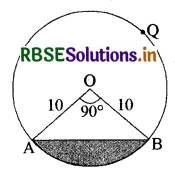
केन्द्रीय कोण (θ) = 90°
लघु त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\pi R^{2} \theta}{360^{\circ}}\)
= 3.14 × 10 × 10 × \(\frac{90^{\circ}}{360^{\circ}}\)
= \(\frac{314}{4}\)
लघु त्रिज्यखण्ड का क्षेत्रफल = \(\frac{314}{4}\) = 78.5 cm
(i) संगत लघु वृत्तखण्ड का क्षेत्रफल = लघु त्रिज्यखण्ड का क्षेत्रफल - ∆AOB का क्षेत्रफल
= 78.5 - \(\frac{1}{2}\) × आधार × ॐनाई
= (78.5 - \(\frac{1}{2}\) × 10 × 10) cm2 [∵ θ = 90°]
= (78.5 - 50) cm²
= 28.5 cm²
∴ संगत लघु वृत्तखण्ड का क्षेत्रफल = 28.5 cm²
(ii) संगत, दीर्घ त्रिज्यखण्ड का क्षेत्रफल

∴ संगत दीर्घ त्रिज्यखण्ड का क्षेत्रफल = 235.5 cm²

प्रश्न 5.
त्रिज्या 21 cm वाले वृत्त का एक चाप केन्द्र पर 60° का कोण अन्तरित करता है। ज्ञात कीजिए :
(i) चाप की लम्बाई
(ii) चाप द्वारा बनाए गए त्रिज्यखण्ड का क्षेत्रफल
(iii) संगत जीवा द्वारा बनाए गए वृत्तखण्ड का क्षेत्रफल।
हल-
(i) प्रश्नानुसार, वृत्त की त्रिज्या (R) = 21 cm
केन्द्रीय कोण (θ) = 60°
चाप की लम्बाई = \(\frac{\theta}{360^{\circ}}\) × 2πR
= \(\frac{60^{\circ}}{360^{\circ}} \times 2 \times \frac{22}{7} \times 21\)
चाप की लम्बाई = 22 cm

(ii) चाप द्वारा बनाए गए त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\pi \mathrm{R}^{2} \theta}{360^{\circ}}\)
= \(\frac{22}{7} \times \frac{21 \times 21 \times 60^{\circ}}{360^{\circ}}\)
= 231 cm²

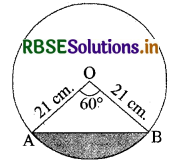
(iii) ∵ ∆OAB समबाहु त्रिभुज है जिसमें (θ) = 60°
∴ वृत्तखण्ड का क्षेत्रफल = त्रिज्यखण्ड का क्षेत्रफल - ∆AOB का क्षेत्रफल
= \(\frac{\pi R^{2} \theta}{360}-\frac{\sqrt{3}}{4}\) (भुजा)²
= 360 - \(\frac{\sqrt{3}}{4}\) × 21 × 21
= (231 - \(\frac{441 \sqrt{3}}{4}\)) cm²
= 231 - 110.25 × 1.732
= 231 - 190.95 लगभग
= 40.05 cm²
अतः वृत्तखण्ड का क्षेत्रफल = 40.05 या (231 - \(\frac{441}{4} \sqrt{3}\)) cm²

प्रश्न 6.
15 cm त्रिज्या वाले एक वृत्त की कोई जीवा केन्द्र पर 60° का कोण अन्तरित करती है। संगत लघु और दीर्घ वृत्तखण्डों के क्षेत्रफल ज्ञात कीजिए।
(π = 3.14 और √3 = 1.73 का प्रयोग कीजिए।)
हल-
प्रश्नानुसार,वृत्त की त्रिज्या (R) = 15 cm
केन्द्रीय कोण (θ) = 60°

∆OAB में; केन्द्रीय कोण θ = 60°
OA = OB = 15 cm
∴ ∠A = ∠B = 60°
∴ ∆OAB समबाहु त्रिभुज है।

दीर्घ वृत्तखण्ड का क्षेत्रफल = वृत्त का क्षेत्रफल - लघु वृत्तखण्ड का क्षेत्रफल
= πR² - 20.43
= 3.14 × 15 × 15 - 20.43
= 706.5 - 20.43
= 686.07 cm²
दीर्घ वृत्तखण्ड का क्षेत्रफल = 686.07 cm²

प्रश्न 7.
त्रिज्या 12 cm वाले एक वृत्त की कोई जीवा केन्द्र पर 120° का कोण अन्तरित करती है। संगत वृत्तखण्ड का क्षेत्रफल ज्ञात कीजिए।
(π = 3.14 और √3 = 1.73 का प्रयोग कीजिए।)
हल-
प्रश्नानुसार, वृत्त की त्रिज्या (R) = 12 cm
केन्द्रीय कोण (θ) = 120°
∆OAM में, OM ⊥ AB
∴ AM = MB = \(\frac{1}{2}\) AB

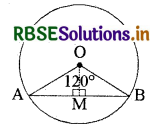
∴ ∠OAM = 30° = ∠OBM
AB = 2AM
⇒ AB = 2 \(\left(\frac{\mathrm{AM}}{\mathrm{OA}}\right)\) OA
⇒ AB = 2 (sin 60°) 12
⇒ AB = 2 × \(\frac{\sqrt{3}}{2}\) × 12
⇒ AB = 12√3 cm
OM = OA\(\left(\frac{\mathrm{OM}}{\mathrm{OA}}\right)\)
= 12 (cos 60°)
= 12 × \(\frac{1}{2}\)
= 6 cm

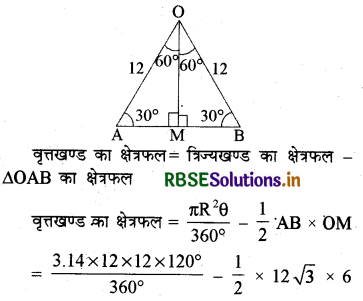
= \(\frac{314}{100} \times \frac{144 \times 120^{\circ}}{360^{\circ}}-36 \sqrt{3}\)
= 150.72 - 36 × 1.73
= (150.72 - 62.28) cm²
= 88.44 cm²
∴ वृत्तखण्ड का क्षेत्रफल = 88.44 cm²

प्रश्न 8.
15 m भुजा वाले एक वर्गाकार घास के मैदान के एक कोने पर लगे खंटे से एक घोड़े को 5 m लम्बी रस्सी से बाँध दिया गया है (देखिए आकृति)। ज्ञात कीजिए :
(i) मैदान के उस भाग का क्षेत्रफल जहाँ घोड़ा घास चर सकता है।
(ii) चरे जा सकने वाले क्षेत्रफल में वृद्धि, यदि घोड़े को 5 m लम्बी रस्सी के स्थान पर 10 m लम्बी रस्सी से बाँध दिया जाए।
(π = 3.14 का प्रयोग कीजिए।)

हल-
प्रश्नानुसार,वर्ग की भुजा = 15 m
(i) खूटे की रस्सी की लम्बाई = रस्सी की त्रिज्या (R) = 5 m
केन्द्रीय कोण (θ) = 90°
त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\pi \mathrm{R}^{2} \theta}{360^{\circ}}\)
= \(\frac{3.14 \times 5 \times 5 \times 90^{\circ}}{360^{\circ}}\)
= \(\frac{3.14 \times 25}{4}\)
= \(\frac{78.5}{4}\)
= 19.625 m²
अतः घोड़े का घास चरने योग्य मैदान का क्षेत्रफल = 19.625 m²

(ii) जब त्रिज्यखण्ड की त्रिज्या 10 m हो जाती है।
त्रिज्यखण्ड की त्रिज्या (R₁) = 10 m
केन्द्रीय कोण (θ) = 90°
∴ त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\pi R_{1}^{2} \theta}{360^{\circ}}\)
= \(\frac{3.14 \times 10 \times 10 \times 90^{\circ}}{360^{\circ}}\)
= \(\frac{314}{100} \times \frac{100 \times 90^{\circ}}{360^{\circ}}\)
= \(\frac{314}{4}\)
= 78.5 m²
∴ चरे जा सकने वाले क्षेत्रफल में वृद्धि = बड़े त्रिज्यखण्ड का क्षेत्रफल - छोटे त्रिज्यखण्ड का क्षेत्रफल
= 78.5 - 19.625
= 58.875 m²
∴ चरे जा सकने वाले क्षेत्रफल में वृद्धि = 58.875 m²

प्रश्न 9.
एक वृत्ताकार बूच (brooch) को चाँदी के तार से बनाया जाना है जिसका व्यास 35 mm है। तार को वृत्त के 5 व्यासों को बनाने में भी प्रयुक्त किया गया है जो उसे 10 बराबर त्रिज्यखण्डों में विभाजित करता है जैसा कि आकृति में दर्शाया गया है। तो ज्ञात कीजिए :
(i) कुल वांछित चाँदी के तार की लम्बाई
(ii) बूच के प्रत्येक त्रिज्यखण्ड का क्षेत्रफल

हल-
प्रश्नानुसार, वृत्त का व्यास (D) = 35 mm
वृत्त की त्रिज्या (R) = \(\frac{35}{2}\) mm
व्यासों की संख्या = 5
बराबर त्रिज्यखण्डों की संख्या = 10
(i) प्रयोग किए गए तार की लम्बाई = 5 व्यासों की लम्बाई + वृत्त (ब्रूच) का परिमाप
= 5(35) + 2πR
= 175 + 2 \(\times \frac{22}{7} \times \frac{35}{2}\)
= 175 + 110
= 285 mm
(ii) ब्रूच के त्रिज्यखण्ड का कोण

अतः ब्रूच के प्रत्येक त्रिज्यखण्ड का क्षेत्रफल = 96.25 mm²

प्रश्न 10.
एक छतरी में आठ ताने हैं, जो बराबर दूरी पर लगे हुए हैं (देखिए आकृति)। छतरी को 45 cm त्रिज्या वाला एक सपाट वृत्त मानते हुए, इसकी दो क्रमागत तानों के बीच का क्षेत्रफल ज्ञात कीजिए।

हल-
प्रश्नानुसार, वृत्त की त्रिज्या = 45 cm
तानों की संख्या = 8
केन्द्रीय कोण (त्रिज्यखण्ड कोण) = \(\frac{360}{8}\) = 45°

अतः दो क्रमागत तानों के बीच का क्षेत्रफल = \(\frac{22275}{28}\) cm²

प्रश्न 11.
किसी कार के दो वाइपर (Wipers) हैं, परस्पर कभी आच्छादित नहीं होते हैं। प्रत्येक वाइपर की पत्ती की लम्बाई 25 cm है और 115° के कोण तक घूम कर सफाई कर सकता है। पत्तियों की प्रत्येक बुहार के साथ जितना क्षेत्रफल साफ हो जाता है, वह ज्ञात कीजिए।
हल-
प्रश्नानुसार, पत्ती की लम्बाई (R) = 25 cm
त्रिज्यखण्ड का कोण (θ) = 115°
वाइपर त्रिज्यखण्ड के रूप में घूमता है।

प्रश्न 12.
जहाजों को समुद्र में जलस्तर के नीचे स्थित चट्टानों की चेतावनी देने के लिए, एक लाइट हाउस (light house) 80° कोण वाले एक त्रिज्यखण्ड में 16.5 km की दूरी तक लाल रंग का प्रकाश फैलाता है। समुद्र के उस भाग का क्षेत्रफल ज्ञात कीजिए जिसमें जहाजों को चेतावनी दी जा सके। (π = 3.14 का प्रयोग कीजिए।)
हल-
त्रिज्यखण्ड कोण (θ) = 80°
त्रिज्यखण्ड की त्रिज्या (R) = 16.5 km

समुद्र के उस भाग का क्षेत्रफल जिसमें जहाजों को चेतावनी दी जा सके अर्थात्
त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\pi \mathrm{R}^{2} \theta}{360^{\circ}}\)
= \(\frac{3.14 \times 16.5 \times 16.5 \times 80^{\circ}}{360^{\circ}}\)
= 189.97 km²
समुद्र के उस भाग का क्षेत्रफल जिसमें जहाजों को चेतावनी दी जा सके = 189.97 km²

प्रश्न 13.
एक गोल मेजपोश पर छः समान डिजाइन बने हुए हैं जैसा कि आकृति में दर्शाया गया है। यदि मेजपोश की त्रिज्या 28 cm है, तो 0.35 रु. प्रति वर्ग सेन्टीमीटर की दर से इन डिजाइनों को बनाने की लागत ज्ञात कीजिए। (√3 = 1.7 का प्रयोग कीजिए)

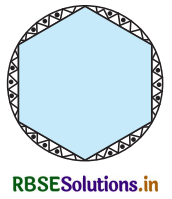
हल-
प्रश्नानुसार समान डिजाइनों की संख्या = 6
डिजाइन की त्रिज्या (R) = 28 cm
प्रत्येक डिजाइन त्रिज्यखण्ड के आकार का है, केन्द्रीय कोण
θ = \(\frac{360^{\circ}}{6}\) = 60°
क्योंकि केन्द्रीय कोण 60° है और OA = OB है।
अतः ∆OAB एक समबाहु त्रिभुज है जिसकी भुजा 28 cm है।

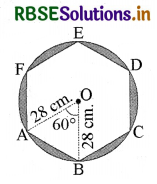
एक छायांकित डिजाइन के भाग का क्षेत्रफल = वृत्तखण्ड का क्षेत्रफल
= त्रिज्यखण्ड OAB का क्षेत्रफल - ∆OAB का क्षेत्रफल
= \(\frac{\pi R^{2} \theta}{360^{\circ}}-\frac{\sqrt{3}}{4}\) (भुजा)²
= \(\left(\frac{22}{7} \times \frac{28 \times 28}{360} \times 60-\frac{1.7}{4} \times 28 \times 28\right)\) cm²
= (410.66 - 333.2) cm²
= 77.46 cm²
एक छायांकित डिजाइन के भाग का क्षेत्रफल = 77.46 cm²
छः डिजाइन के भागों का क्षेत्रफल = 6[एक डिजाइन के भाग का क्षेत्रफल]
= 6[77.46]
= 464.76 cm²
∵ 1 cm² डिजाइन बनाने का खर्च = 0.35 रु.
∴ 464.76 cm² डिजाइन बनाने का खर्च = 0.35 × 464.76 रु. = 162.68 रु.
अतः डिजाइनों को बनाने की लागत = 162.68 रु.

प्रश्न 14.
निम्नलिखित में सही उत्तर चुनिए :
त्रिज्या R वाले वृत्त के उस त्रिज्यखण्ड का क्षेत्रफल जिसका कोण p° है, निम्नलिखित है :
(A) \(\frac{p}{180} \times 2 \pi R\)
(B) \(\frac{p}{180} \times \pi \mathbf{R}^{2}\)
(C) \(\frac{p}{360} \times 2 \pi \mathbf{R}\)
(D) \(\frac{p}{720} \times 2 \pi \mathrm{R}^{2}\)
हल-
त्रिज्यखण्ड का कोण (θ) = p°
वृत्त की त्रिज्या = R
त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\pi \mathrm{R}^{2} \theta}{360^{\circ}}\)
= \(\frac{\pi \mathrm{R}^{2} \times p^{\circ}}{360^{\circ}}\)
= \(\frac{2 \pi \mathrm{R}^{2} \times p^{\circ}}{720^{\circ}}\)
∴ सही विकल्प = (D)