RBSE Solutions for Class 10 Maths Chapter 11 रचनाएँ Ex 11.1

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 11 रचनाएँ Ex 11.1 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 11 रचनाएँ Ex 11.1

निम्न में से प्रत्येक के लिए रचना का औचित्य भी दीजिए:

Ex 11.1 Class 10 In Hindi प्रश्न 1.
7.6 cm लम्बा एक रेखाखण्ड खींचिए और इसे 5 : 8 अनुपात में विभाजित कीजिए। दोनों भागों को मापिए।
हल-
रचना के चरण :

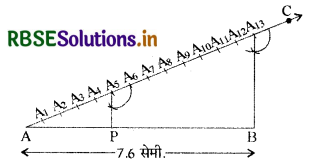
1. सर्वप्रथम रेखाखण्ड AB = 7.6 cm. खींचिए।
2. अब किरण AC खींचिए जो AB के साथ कोई भी न्यून कोण बनाए।
3. किरण AC पर, A से शुरू करके 5 + 8 = 13 बराबर रेखाखण्ड अंकित करें :
AA₁, A₁A₂, A₂A₃, A₃A₄, A₄A₅, A₅A₆, A₆A₇, A₇A₈, A₈A₉, A₉,A₁₀, A₁₀A₁₁, A₁₁A₁₂ और A₁₂A₁₃
4. अब AB को मिलाएँ।
5. A₅ से A₅P || A₁₃B खींचें जो AB से P पर मिले।
6. इस प्रकार, P, AB को 5 : 8 के अनुपात में बाँटता है।
दोनों भागों को मापने पर AP = 2.9 cm और PB = 4.7 cm
स्पष्टीकरण-
∆ABA₁₃ में, PA₅ || BA₁₃
∴ ∆APA₅ ~ ∆ABA₁₃
⇒ \(\frac{\mathrm{AP}}{\mathrm{PB}}=\frac{\mathrm{AA}_{5}}{\mathrm{~A}_{5} \mathrm{~A}_{13}}=\frac{5}{8}\)
⇒ AP : PB = 5 : 8

Class 10 Maths Chapter 11.1 Hindi Medium प्रश्न 2.
4 cm, 5 cm और 6 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर इसके समरूप एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की \(\frac{2}{3}\) गुनी हों।
हल-
रचना के चरण : 
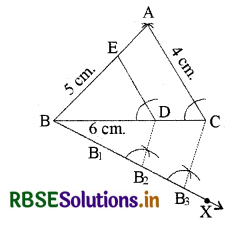
1. सर्वप्रथम एक रेखाखण्ड BC = 6 cm खींचिए।
2. अब B को केन्द्र मानकर, 5 cm के बराबर त्रिज्या भरकर एक चाप काटिए।
3. C को केन्द्र मानकर, 4 cm के बराबर त्रिज्या भरकर, पहले वाले चाप को A पर काटते हुए चाप लगाइए।
4. AB और AC को मिलाइए, इस तरह ∆ABC अभीष्ट त्रिभुज होगा।
5. BC के नीचे, एक न्यून कोण CBX बनाइए।
6. BX के साथ, तीन बिन्दु B₁, B₂ और B₃ इस प्रकार अंकित कीजिए कि BB₁ = B₁B₂ = B₂B₃ हो जाएँ।
7. अब B₃C को मिलाइए।
8. B₂ से B₂D || B₃C खींचिए जो BC को D पर मिलता है।
9. D से ED || AC खींचिए जो BA को E पर मिलता है।
इस प्रकार ∆EBD अभीष्ट त्रिभुज होगा जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac{2}{3}\) गुनी होंगी।

स्पष्टीकरण-
चूँकि DE || CA
∴ ∆ABC ~ ∆EBD
और, \(\frac{\mathrm{EB}}{\mathrm{AB}}=\frac{\mathrm{BD}}{\mathrm{BC}}=\frac{\mathrm{DE}}{\mathrm{CA}}=\frac{2}{3}\)
अतः, हमें नया त्रिभुज प्राप्त होता है जो दिए गए त्रिभुज के समान होता है, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac{2}{3}\) गुनी के बराबर होती हैं।

11.1 Class 10 In Hindi प्रश्न 3.
5 cm, 6 cm और 7 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की \(\frac{7}{5}\) गुनी हों।
हल-
रचना के चरण :
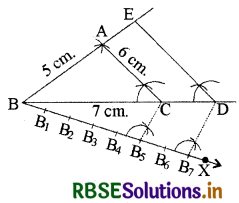
1. सर्वप्रथम दिए हुए मान से ∆ABC की रचना कीजिए, जिसमें BC = 7 cm, CA = 6 cm और AB = 5 cm.
2. अब BC के नीचे, न्यून कोण CBX बनाइए।
3. BX के साथ, सात बिन्दु चिह्नित कीजिए : B₁, B₂, B₃, B₄, B₅, B₆, और B₇
इस प्रकार BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ = B₅B₆ = B₆B₇
4. अब B₅C को मिलाइए।
5. B₇ से होकर जाने वाली B₇D || B₅C खींचिए, BC को D तक बढ़ाकर मिलाइए।
6. D से होकर जाने वाली DE || CA खींचिए, जो बढ़ाए गए BA से E पर मिलता है।
इस प्रकार ∆EBD अभीष्ट त्रिभुज होगा, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac{7}{5}\) गुनी होंगी।

स्पष्टीकरण-
चूँकि DE || CA
∴ ∆ABC ~ ∆EBD
और \(\frac{E B}{A B}=\frac{B D}{B C}=\frac{D E}{C A}=\frac{7}{5}\)
अत्तः हमें नया त्रिभुज दिए गए त्रिभुज के समरूप प्राप्त होता है, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac{7}{5}\) गुनी होती हैं।

Math Class 10 Chapter 11.1 In Hindi प्रश्न 4.
आधार 8 cm तथा ऊँचाई 4 cm के एक समद्विबाहु त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ इस समद्विबाहु त्रिभुज की संगत भुजाओं की \(1 \frac{1}{2}\) गुनी हों।
हल-
रचना के चरण :
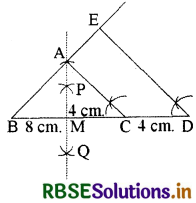
1. सर्वप्रथम BC = 8 cm खींचिए।
2. रेखाखण्ड BC के लम्ब द्विभाजक PQ की रचना कीजिए जो BC पर M से मिले।
3. MP के साथ, MA = 4 cm काटिए।
4. BA और CA को मिलाइए, अब प्राप्त ∆ABC ही अभीष्ट त्रिभुज है।
5. BC को D तक बढ़ाइए, इस तरह कि BD = 12 cm
6. DE || CA खींचिए, BA को आगे बढ़ाकर E पर मिलाइए। 
तब, ∆EBD ही अभीष्ट त्रिभुज होगा।

स्पष्टीकरण-
चूँकि DE || CA
∴ ∆ABC ~ ∆EBD
और \(\frac{\mathrm{EB}}{\mathrm{AB}}=\frac{\mathrm{DE}}{\mathrm{CA}}=\frac{\mathrm{BD}}{\mathrm{BC}}=\frac{12}{8}=\frac{3}{2}\)
अतः हमें नया त्रिभुज दिए गए त्रिभुज के समरूप प्राप्त होता है, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac{3}{2}\) गुनी अर्थात् \(1\frac{1}{2}\) गुनी होती हैं।

10th Class Math 11.1 In Hindi प्रश्न 5.
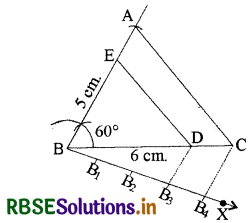
एक त्रिभुज ABC बनाइए जिसमें BC = 6 cm, AB = 5 cm और ∠ABC = 60° हो। फिर एक त्रिभुज की रचना कीजिए जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac{3}{4}\) गुनी हों।
हल-
रचना के चरण :
1. सर्वप्रथम दिए गए मानों से ∆ABC की रचना कीजिए जिसमें BC = 6 cm, ∠ABC = 60° और AB = 5 cm.
2. अब BC के नीचे एक न्यून कोण ∠CBX बनाइए।
3. BX के साथ, चार बिन्दु B₁, B₂, B₃, और B₄ लगाइए। इस तरह BB₁ = B₁B₂ = B₂B₃ = B₃B₄
4. फिर B₄C को मिलाइए और B₃D || B₄C खींचिये।
5. अब D से, ED || AC खींचिए जो BA को E पर मिलता है।
फिर ∆EBD अभीष्ट त्रिभुज होगा जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac{3}{4}\) गुनी होंगी।
स्पष्टीकरण-
चूँकि DE || CA
∴ ∆ABC ~ ∆EBD
और, \(\frac{\mathrm{EB}}{\mathrm{AB}}=\frac{\mathrm{BD}}{\mathrm{BC}}=\frac{\mathrm{DE}}{\mathrm{CA}}=\frac{3}{4}\)

अतः हमें नया त्रिभुज दिए गए त्रिभुज के समरूप प्राप्त होता है, जिसकी भुजाएँ ∆ABC संगत भुजाओं की \(\frac{3}{4}\) गुनी होती हैं।

Class 10 Maths Exercise 11.1 Solutions In Hindi प्रश्न 6.
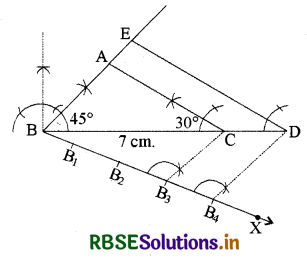
एक त्रिभुज ABC बनाइए, जिसमें BC = 7 cm, ∠B = 45०, ∠A = 105० हो। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac{4}{3}\) गुनी हों।
हल-
रचना के चरण :
1. सर्वप्रथम दिए गए मान से ∆ABC की रचना कीजिए जिसमें
BC = 7 cm, ∠B = 45°, ∠C = 180° - (∠A + ∠B)
∠C = 180° - (105° + 45°)
= 180° - 150°
= 30°
2. अब BC के नीचे एक न्यून कोण ∠CBX खींचिए।
3. BX के साथ, चार बिन्दु अंकित कीजिए : B₁, B₂, B₃ और B₄ । इस तरह BB₁ = B₁B₂ = B₂B₃ = B₃B₄
4. फिर BC मिलाइए।
5. B₄ से, B₄D || B₃C खींचिए जो बढ़ाए गए BC को D पर मिलता है।
6. D से, ED || AC खींचिए, BA को E तक बढ़ाकर मिलाइए।
फिर ∆EBD अभीष्ट त्रिभुज होगा जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac{4}{3}\) गुनी होंगी।
स्पष्टीकरण-
चूँकि, DE || CA
∴ ∆ABC ~ ∆EBD
और, \(\frac{\mathrm{EB}}{\mathrm{AB}}=\frac{\mathrm{BD}}{\mathrm{BC}}=\frac{\mathrm{DE}}{\mathrm{CA}}=\frac{4}{3}\)

अतः हमें नया त्रिभुज दिए गए त्रिभुज के समरूप प्राप्त होता है, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac{4}{3}\) गुनी होती हैं।

Exercise 11.1 Class 10 Ncert Solutions In Hindi प्रश्न 7.
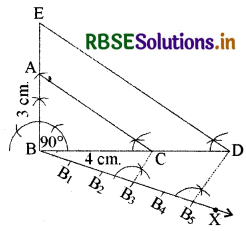
एक समकोण त्रिभुज की रचना कीजिए, जिसकी भुजाएँ (कर्ण के अतिरिक्त) 4 cm तथा 3 cm लम्बाई की हों। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की \(\frac{5}{3}\) गुनी हों।
हल-
रचना के चरण :
1. सर्वप्रथम दिए गए मानों से ∆ABC की रचना कीजिए, जिसमें BC = 4 cm, ∠B = 90° और BA = 3 cm.
2. अब BC के नीचे एक न्यून कोण CBX खींचिए।
3. BX के साथ पाँच बिन्दु अंकित कीजिए : B₁, B₂, B₃, B₄ और B₅ इस तरह BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅
4. B₃C को मिलाइए।
5. B₅ से, B₅D || B₃C खींचिए जो बढ़ाए गए BC को D पर मिलता है।
6. D से, ED || AC खींचिए, BA को E तक बढ़ाकर मिलाइए।
तब, ∆EBD अभीष्ट त्रिभुज होगा, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac{5}{3}\) गुनी होंगी।
स्पष्टीकरण-
चूँकि, DE || CA
∴ ∆ABC ~ ∆EBD
और, \(\frac{\mathrm{EB}}{\mathrm{AB}}=\frac{\mathrm{BD}}{\mathrm{BC}}=\frac{\mathrm{DE}}{\mathrm{CA}}=\frac{5}{3}\)

अतः हमें नया त्रिभुज दिए गए त्रिभुज के समरूप प्राप्त होता है, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac{5}{3}\) गुनी होती हैं।