RBSE Solutions for Class 10 Maths Chapter 1 वास्तविक संख्याएँ Ex 1.4

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 1 वास्तविक संख्याएँ Ex 1.4 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 1 वास्तविक संख्याएँ Ex 1.4

प्रश्न 1.
बिना लम्बी विभाजन प्रक्रिया किए बताइए कि निम्नलिखित परिमेय संख्याओं के दशमलव प्रसार सांत हैं या असांत आवर्ती हैं-
(i) \(\frac{13}{3125}\)
हल-
माना कि x = \(\frac{13}{3125}\) ......(i)
अब (i) की x = \(\frac{p}{q}\) से तुलना करने पर
यहाँ p = 13 तथा q = 3125
अब q अर्थात् 3125 के अभाज्य गुणनखण्ड
= 5 × 5 × 5 × 5 × 5
= 5⁵ × 2⁰
जो कि 5^m × 2ⁿ के रूप का है। यहाँ m = 5 तथा n = 0 तथा ये ऋणेत्तर पूर्णांक हैं। अतः
x = \(\frac{13}{3125}\) का दशमलव प्रसार सांत है।

(ii) \(\frac{17}{8}\)
हल-
माना कि x = \(\frac{17}{8}\) ......(i)
अब (i) की x = \(\frac{p}{q}\) से तुलना करने पर यहाँ p = 17 तथा q = 8
अब q अर्थात् 8 के अभाज्य गुणनखण्ड
= 2 × 2 × 2
= 2³
= 2³ × 5⁰
जो कि 2ⁿ × 5^m के रूप का है। यहाँ n = 3 तथा m = 0 तथा ये ऋणेत्तर पूर्णांक हैं। अतः
x = \(\frac{17}{8}\) का दशमलव प्रसार सांत है।

(iii) \(\frac{64}{455}\)
हल-
माना कि x = \(\frac{64}{455}\) ......(i)
अब (i) की तुलना x = \(\frac{p}{q}\) से करने पर यहाँ p = 64 तथा q = 455
अब q अर्थात् 455 के अभाज्य गुणनखण्ड = 5 × 7 × 13
जो कि 2ⁿ × 5^m के रूप का नहीं है।
चूंकि हर में 2 अथवा 5 के अतिरिक्त अभाज्य गुणनखण्ड 7 और 13 भी हैं।
अतः x = \(\frac{64}{455}\) का दशमलव प्रसार असांत आवर्ती है।

(iv) \(\frac{15}{1600}\)
हल-
माना कि x = \(\frac{15}{1600}\) ......(i)
अब (i) की तुलना x = \(\frac{p}{q}\) से करने पर यहाँ p = 15  तथा q = 1600
अतः q अर्थात् 1600 के अभाज्य गुणनखण्ड
= 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5
= 2⁶ × 5²
जो कि 2ⁿ × 5^m के रूप का है। यहाँ m = 2 तथा n = 6 तथा ये ऋणेत्तर पूर्णांक हैं। अतः
x = \(\frac{15}{1600}\) का दशमलव प्रसार सांत है।

(v) \(\frac{29}{343}\)
हल-
माना कि x = \(\frac{29}{343}\) .......(i)
अब (i) की तुलना x = \(\frac{p}{q}\) से करने पर यहाँ p = 29 तथा q = 343
अतः q अर्थात् 343 के अभाज्य गुणनखण्ड
= 7 × 7 × 7
= 7³
जो कि 2ⁿ × 5^m के रूप का नहीं है। चूंकि हर में 2 अथवा 5 के अभाज्य गुणनखण्ड नहीं हैं।
अतः x = \(\frac{29}{343}\)
का दशमलव प्रसार असांत आवर्ती है।

(vi) \(\frac{23}{2^{3} 5^{2}}\)
हल-
माना कि x = \(\frac{23}{2^{3} 5^{2}}\) .......(i)
अब (i) की तुलना x = \(\frac{p}{q}\) से करने पर यहाँ p = 23 तथा q = 2³5²
अतः q अर्थात् 2352 के अभाज्य गुणनखण्ड = 2³ × 5²
जो कि 2ⁿ × 5^m के रूप का है जहाँ n = 3 तथा m = 2 तथा ये ऋणेत्तर पूर्णांक हैं। अतः
x = \(\frac{23}{2^{3} 5^{2}}\) का दशमलव प्रसार सांत है।

(vii) \(\frac{129}{2^{2} 5^{7} 7^{5}}\)
हल-
माना कि x = \(\frac{129}{2^{2} 5^{7} 7^{5}}\) ..... (i)
अब (i) की तुलना x = \(\frac{p}{q}\) से करने पर यहाँ p = 129 तथा q = 2²5⁷7⁵
अतः q अर्थात् 225775 के अभाज्य गुणनखण्ड = 2² × 5⁷ × 7⁵
जो कि 2ⁿ × 5^m के रूप का नहीं है। चूंकि गुणनखण्ड 7, 2 या 5 के अतिरिक्त हैं।
अत: x = \(\frac{129}{2^{2} 5^{7} 7^{5}}\) का दशमलव प्रसार असांत आवर्ती है।

(viii) \(\frac{6}{15}\)
हल-
माना कि x = \(\frac{6}{15}=\frac{2}{5}\) ......(i)
अब (i) की तुलना x = \(\frac{p}{q}\) से करने पर यहाँ p = 2 तथा q = 5
अतः q अर्थात् 5 के अभाज्य गुणनखण्ड = 2⁰ × 5¹
जो कि 2ⁿ × 5^m के रूप का है जहाँ n = 0 तथा m = 1 तथा ये ऋणेत्तर पूर्णांक हैं। अतः
x = \(\frac{6}{15}\) का दशमलव प्रसार सांत है।

(ix) \(\frac{35}{50}\)
हल-
माना कि x = \(\frac{35}{50}=\frac{7}{10}\) .......(i)
अब (i) की तुलना x = \(\frac{p}{q}\) से करने पर यहाँ p = 7 और q = 10
अतः q अर्थात् 10 के अभाज्य गुणनखण्ड
= 2 × 5
= 2¹ × 5¹
जो कि 2ⁿ × 5^m के रूप का है जहाँ n = 1 तथा m = 1 और ये ऋणेत्तर पूर्णांक हैं। अतः
x = \(\frac{7}{10}\) या \(\frac{35}{50}\) का दशमलव प्रसार सांत है।

(x) \(\frac{77}{210}\)
हल-
माना कि x = \(\frac{77}{210}=\frac{11}{30}\) .......(i)
अब (i) की तुलना x = \(\frac{p}{q}\) से करने पर यहाँ p = 11 और q = 30
अतः q अर्थात् 30 के अभाज्य गुणनखण्ड = 2 × 3 × 5
जो कि 2ⁿ × 5^m के रूप का नहीं है। चूँकि हर में 12 और 5 के अतिरिक्त गुणनखण्ड 3 है।
अतः x = \(\frac{77}{210}\) का दशमलव प्रसार असांत आवर्ती है।

प्रश्न 2.
ऊपर दिए गए प्रश्न में उन परिमेय संख्याओं के दशमलव प्रसारों को लिखिए जो सांत हैं।
हल-

प्रश्न 3.
कुछ वास्तविक संख्याओं के दशमलव प्रसार नीचे दर्शाए गए हैं। प्रत्येक स्थिति के लिए निर्धारित कीजिए कि यह संख्या परिमेय संख्या है या नहीं। यदि यह परिमेय संख्या है और \(\frac{p}{q}\) के रूप की है तो q के अभाज्य गुणनखण्डों के बारे में आप क्या कह सकते हैं?
(i) 43.123456789
हल-
(i) माना कि x = 43.123456789

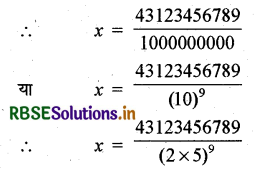
जो कि \(\frac{p}{q}\) के रूप की एक परिमेय संख्या है।
अतः q के अभाज्य गुणनखण्ड 2 या 5 या दोनों होंगे।

(ii) 0.120120012000120000...
हल-
माना कि x = 0.120120012000120000...
दी गई संख्या से स्पष्ट है कि यह एक अपरिमेय संख्या है।
चूँकि इस संख्या का दशमलव प्रसार असांत एवं अनावर्ती है।
∴ इसको \(\frac{p}{q}\) के रूप में नहीं लिखा जा सकता है।
∴ यह संख्या परिमेय नहीं है।

(iii) \(43 . \overline{123456789}\)
हल-
माना कि x = \(43 . \overline{123456789}\)
x = 43.123456789123456789  ....... (i)
दोनों पक्षों को 10⁹ से गुणा करने पर
10⁹ x = 43123456789.123456789 ...... (ii)
(ii) में से (i) को घटाने पर
(10⁹ - 1) x = 43123456746
999999999x = 43123456746
x = \(\frac{43123456746}{999999999}\)
जो कि \(\frac{p}{q}\) के रूप की एक परिमेय संख्या है।
x = \(\frac{4791495194}{111111111}\) = \(\frac{4791495194}{9(123456789)}\)
अतः q के अभाज्य गुणनखण्ड 2 या 5 के अतिरिक्त एक और गुणनखण्ड होगा।
अतः दी गई संख्या परिमेय है और q के अभाज्य गुणनखण्ड 2 या 5 के अतिरिक्त भी है।