RBSE Solutions for Class 10 Maths Chapter 1 वास्तविक संख्याएँ Ex 1.3

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 1 वास्तविक संख्याएँ Ex 1.3 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 1 वास्तविक संख्याएँ Ex 1.3

प्रश्न 1.
सिद्ध कीजिए कि √5 एक अपरिमेय संख्या है।
हल-
माना कि √5 एक परिमेय संख्या है।
अतः हम ऐसे दो पूर्णांक r व s प्राप्त कर सकते हैं जहाँ s ≠ 0 तथा
√5 = \(\frac{r}{s}\)
अब पुनः माना कि r व s में, 1 के अतिरिक्त अन्य कुछ गुणनखण्ड हैं तो हम उस उभयनिष्ठ गुणनखण्ड से r और s को विभाजित करके √5 = \(\frac{a}{b}\) प्राप्त कर सकते हैं।
यहाँ a और b सहअभाज्य है।
अर्थात् b√5 = a
दोनों पक्षों का वर्ग करने पर
⇒ (b√5)² = a²
⇒ b2(√5)² = a²
⇒ 5b² = a² .......(i)
अतः 5, a² को विभाजित करता है।
प्रमेय 1.3 के अनुसार यदि एक अभाज्य संख्या p, a² को विभाजित करती है तो p, a को भी विभाजित करेगी, जहाँ a एक धनात्मक पूर्णांक है।
⇒ 5, a को भी विभाजित करता है। ........(ii)
अतः a = 5c जहाँ c कोई पूर्णांक है।
a का मान (i) में रखने पर
5b² = (5c)²
5b² = 25c²
b² = 5c²
या 5c² = b²
⇒ 5, b² को विभाजित करता है।
प्रमेय के अनुसार 5, b को भी विभाजित करता है। .......(iii)
(ii) व (iii) से, a और b का कम से कम एक उभयनिष्ठ गुणनखण्ड 5 है।
परन्तु यह इस तथ्य का विरोधाभासी है कि a और b अविभाज्य हैं या इनके 1 के अतिरिक्त अन्य कोई उभयनिष्ठ गुणनखण्ड हैं।
अतः हमारी कल्पना कि √5 एक परिमेय संख्या है, असत्य है।
अर्थात् √5 एक अपरिमेय संख्या है। (इतिसिद्धम्)

प्रश्न 2.
सिद्ध कीजिए कि 3 + 2√5 एक अपरिमेय संख्या है।
हल-
माना कि 3 + 2√5 एक परिमेय संख्या है।
अतः हम अविभाज्य संख्या a और b प्राप्त कर सकते हैं जहाँ a और b पूर्णांक हैं कि b ≠ 0 तथा

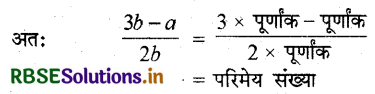
अतः (i) से स्पष्ट है कि √5 एक परिमेय संख्या है।
परन्तु यह तथ्य इस कथन का खण्डन करता है कि √5 एक अपरिमेय संख्या है।
अर्थात् यह कल्पना असत्य है।
अतः दी गई संख्या 3 + 2√5 एक अपरिमेय संख्या है। (इतिसिद्धम्)

प्रश्न 3.
सिद्ध कीजिए कि निम्नलिखित संख्याएँ अपरिमेय हैं-
(i) \(\frac{1}{\sqrt{2}}\)
हल-
\(\frac{1}{\sqrt{2}}\)
प्रश्न में दिए गए कथन के विपरीत माना कि \(\frac{1}{\sqrt{2}}\) एक परिमेय संख्या है।
अतः हम अविभाज्य पूर्णांक a और b (b ≠ 0) प्राप्त कर सकते हैं अर्थात्
\(\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{2}\)
या \(\frac{\sqrt{2}}{2}=\frac{a}{b}\)
या √2 = \(\frac{2 a}{b}\) ....... (i)
क्योंकि दो पूर्णांकों का भागफल एक परिमेय संख्या होती है।
अतः \(\frac{2 a}{b}\) = एक परिमेय संख्या
(i) से √2 भी एक परिमेय संख्या है। परन्तु यह कथन असत्य है। अर्थात् हमारी कल्पना असत्य है।
अतः \(\frac{1}{\sqrt{2}}\) एक अपरिमेय संख्या है। (इतिसिद्धम्)

(ii) 7√5
हल-
7√5
माना कि दी गई संख्या 7√5 एक परिमेय संख्या है।
अतः हम ऐसे दो पूर्णांक a और b (b ≠ 0) प्राप्त कर सकते हैं कि
7√5 = \(\frac{a}{b}\)
या 7b√5 = a
या √5 = \(\frac{a}{7 b}\) ......(i)
चूँकि (i) में a, 7 और b सभी पूर्णांक हैं तथा दो पूर्णांकों का भाग भी एक परिमेय संख्या होती है। अर्थात्
\(\frac{a}{7 b}\) = एक परिमेय संख्या
अतः (i) से √5 = एक परिमेय संख्या
जो कि कथन √5 एक अपरिमेय संख्या है, का विरोधाभासी कथन है।
अर्थात् हमारी कल्पना असत्य है। अतः 7√5 एक अपरिमेय संख्या है। (इतिसिद्धम्)

(iii) 6 + √2
हल-
6 + √2
माना कि 6 + √2 एक परिमेय संख्या है।
अतः हम ऐसी सह-अभाज्य संख्याएँ a और b (b ≠ 0) ज्ञात कर सकते हैं कि
6 + √2 = \(\frac{a}{b}\)
या √2 = \(\frac{a}{b}\) - 6
या √2 = \(\frac{a-6 b}{b}\) ........(i)
चूँकि a तथा b पूर्णांक हैं अतः \(\frac{a-6 b}{b}\) भी एक पूर्णांक संख्या होगी क्योंकि पूर्णांकों की बाकी तथा पूर्णांकों का भाग भी पूर्णांक होता है। अर्थात्
\(\frac{a-6 b}{b}\) = एक परिमेय संख्या
∴ (i) से √2 = एक परिमेय संख्या
परन्तु यह कथन कि √2 एक अपरिमेय संख्या होती है, का विरोधाभासी कथन है।
अतः हमारी कल्पना असत्य है। अर्थात् 6 + √2 एक अपरिमेय संख्या है। (इतिसिद्धम्)